[Click here for a PDF version of this post]
Motivation.
In a fun twitter/x post, we have a Green’s function solution to a constant acceleration problem with drag. The post is meant to be a joke, as the stated problem is: “A boy drops a ball from a height \( h \). What is the speed of the ball when it reaches the floor (no drag)?”
The joke is that nobody would solve this problem using Green’s functions, and nobody would solve this function using Green’s functions for the more general case, allowing for drag. Instead, you’d just solve this using energy balance, which makes the problem trivial.
That said, there are actually lots of cool ideas in the Green’s function method on the joke side of the solution.
So let’s play along with the joke and solve the general damped problem with Green’s functions. Along the way, we can fill in the missing details, and also explore some supplemental ideas that are worth understanding.
Setup.
The equation of motion is
\begin{equation}\label{eqn:greensDropWithResistance:20}
m \frac{d^2 \Bx}{dt^2} = – \gamma \frac{d \Bx}{dt} – m \Bg,
\end{equation}
where \( \Bg \) is a constant (positively oriented) force. The first detail that needs to be included, is that this isn’t the differential equation for the stated problem, and will become problematic should we attempt to apply Green’s function methods. We have to account for the “boy drops” part of the problem statement, and solve with a different forcing function, namely
\begin{equation}\label{eqn:greensDropWithResistance:40}
m \frac{d^2 \Bx}{dt^2} = – \gamma \frac{d \Bx}{dt} – m \Bg \Theta(t).
\end{equation}
This revised model of the system begins the application of the constant (gravitational) force, at time \( t = 0 \). This is now a system that will yield to Green’s function methods.
Fourier transform solution.
The joke solution has strong hints that Fourier transform methods were part of the story. In particular, it appears that the following definitions of the transform pair were used
\begin{equation}\label{eqn:greensDropWithResistance:60}
\begin{aligned}
\hatU(\omega) = F(u(t)) &= \int_{-\infty}^\infty u(t) e^{-i\omega t} dt \\
u(t) = F^{-1}(\hatU(\omega)) &= \inv{2\pi} \int_{-\infty}^\infty \hatU(\omega) e^{i\omega t} d\omega.
\end{aligned}
\end{equation}
However, if we are using Fourier transforms, why bother with Green’s functions? Instead, we can just solve for the system response using Fourier transforms. When looking for the system response, we usually pose the problem with more generality. For example, instead of the specific theta-weighted constant gravitational forcing function above, we seek to find the solution of
\begin{equation}\label{eqn:greensDropWithResistance:80}
m \frac{d^2 \Bx}{dt^2} + \gamma \frac{d \Bx}{dt} = \BF(t).
\end{equation}
We start by assuming that the Fourier transforms of \( \Bx(t), \BF(t) \) are \( \hat{\BX}(\omega), \hat{\BF}(\omega) \) so
\begin{equation}\label{eqn:greensDropWithResistance:100}
\Bx(t) = \inv{2\pi} \int_{-\infty}^\infty e^{i\omega t} \hat{\BX}(\omega) d\omega.
\end{equation}
Derivatives of this presumed Fourier representation are trivial
\begin{equation}\label{eqn:greensDropWithResistance:120}
\begin{aligned}
\Bx'(t) &= \inv{2\pi} \int_{-\infty}^\infty \lr{ i\omega } e^{i\omega t} \hat{\BX}(\omega) d\omega \\
\Bx”(t) &= \inv{2\pi} \int_{-\infty}^\infty \lr{ i\omega }^2 e^{i\omega t} \hat{\BX}(\omega) d\omega,
\end{aligned}
\end{equation}
so the frequency representation of our system is
\begin{equation}\label{eqn:greensDropWithResistance:140}
\inv{2\pi} \int_{-\infty}^\infty \lr{ m \lr{ i\omega }^2 + \gamma \lr{ i\omega} } e^{i\omega t} \hat{\BX}(\omega) d\omega
=
\inv{2\pi} \int_{-\infty}^\infty e^{i\omega t} \hat{\BF}(\omega) d\omega,
\end{equation}
or
\begin{equation}\label{eqn:greensDropWithResistance:160}
\hat{\BX}(\omega) = \frac{\hat{\BF}(\omega)}{-m \omega^2 + i \omega \gamma}.
\end{equation}
We now only have to inverse Fourier transform to find a solution, namely
\begin{equation}\label{eqn:greensDropWithResistance:180}
\begin{aligned}
\Bx(t)
&= \inv{2\pi} \int_{-\infty}^\infty e^{i\omega t} \frac{\hat{\BF}(\omega)}{-m \omega^2 + i \omega \gamma} d\omega \\
&= \inv{2\pi} \int_{-\infty}^\infty e^{i\omega t} \frac{1}{-m \omega^2 + i \omega \gamma} d\omega
\int_{-\infty}^\infty \BF(t’) e^{-i \omega t’} dt’ \\
&= \int_{-\infty}^\infty \lr{ -\inv{2\pi} \int_{-\infty}^\infty \frac{ e^{i\omega (t-t’)} }{m \omega^2 – i \omega \gamma} d\omega }F(t’) dt’,
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:greensDropWithResistance:200}
\Bx(t) = \int_{-\infty}^\infty G(t – t’) \BF(t’) dt’,
\end{equation}
where
\begin{equation}\label{eqn:greensDropWithResistance:220}
G(\tau) = -\inv{2\pi} \int_{-\infty}^\infty \frac{ e^{i\omega \tau} }{\omega\lr{ m \omega – i \gamma}} d\omega.
\end{equation}
We’ve been fast and loose above, swapping order of integration without proper justification, and have assumed that all Fourier transforms and inverse transforms exist. Given all those assumptions, we now have a general solution for the system, requiring only the convolution of our driving force \( F(t) \) with the system response function \( G(t) \). The only caveat is that we have to be able to perform the integral for the system response function, and that integral does not exist.
There are lots of integrals that do not strictly exist when playing the fast and loose physicist game with Fourier transforms. One such example can be found by looking at any transform pair. For example, given \( u(t) = F^{-1}(\hatU(\omega)) \), we have
\begin{equation}\label{eqn:greensDropWithResistance:240}
\begin{aligned}
u(t)
&= \inv{2\pi} \int_{-\infty}^\infty \hatU(\omega) e^{i\omega t} d\omega \\
&= \inv{2\pi} \int_{-\infty}^\infty \lr{ \int_{-\infty}^\infty u(t’) e^{-i\omega t’} dt’ } e^{i\omega t} d\omega \\
&= \int_{-\infty}^\infty u(t’) \lr{ \inv{2\pi} \int_{-\infty}^\infty e^{i\omega (t-t’)} d\omega } dt’.
\end{aligned}
\end{equation}
This is exactly the sort of integration order swapping that we did to find the system response function above, and we are left with a statement that \( f(t) \) is the convolution of \( f(t) \), with another, also non-integrable, convolution kernel. Any physics student will recognize that kernel as a representation of the Dirac delta function, and without blinking, would just write
\begin{equation}\label{eqn:greensDropWithResistance:260}
\delta(\tau) = \inv{2\pi} \int_{-\infty}^\infty e^{i\omega \tau} d\omega,
\end{equation}
without worrying that it is not possible to evaluate this integral. Somebody who is trying to use the right mathematical language, would say that this isn’t a function, but is, instead a distribution. Just like this delta function distribution, our system response integral, something that we also cannot actually evaluate in a strict sense, is a distribution. It’s a beastie that has delta function like characteristics, and if we want to try to integrate it, we have to play sneaky games.
Let’s put off evaluating that integral for now, and return to the Green’s function description of the story.
The Green’s function picture.
Using Fourier transforms, we found that it theoretically possible to find a convolution solution to the system, and found the convolution kernel for the system. The rough idea behind Green’s functions is to assume that such a convolution exists, say
\begin{equation}\label{eqn:greensDropWithResistance:280}
\Bx(t) = \Bx_0(t) + \int_{-\infty}^\infty G(t,t’) \BF(t’) dt’,
\end{equation}
where \( \Bx_0(t) \) is any solution of the homogeneous problem satisfying, in this case,
\begin{equation}\label{eqn:greensDropWithResistance:300}
m \frac{d^2}{dt^2} \Bx_0(t) + \gamma \frac{d}{dt} \Bx_0(t) = 0,
\end{equation}
and \( G(t,t’) \) is a convolution kernel, representing the system response, to be determined.
If we plug this presumed solution into our differential equation, we find
\begin{equation}\label{eqn:greensDropWithResistance:320}
\int_{-\infty}^\infty \lr{
m \frac{\partial^2}{\partial t^2} G(t,t’)
+ \gamma \frac{\partial}{\partial t} G(t,t’)
} \BF(t’) dt’
=
\BF(t),
\end{equation}
but
\begin{equation}\label{eqn:greensDropWithResistance:340}
\BF(t) = \int_{-\infty}^\infty \BF(t’) \delta(t – t’) dt’,
\end{equation}
so, if we can find \( G \) satisfying
\begin{equation}\label{eqn:greensDropWithResistance:360}
m \frac{\partial^2}{\partial t^2} G(t,t’) + \gamma \frac{\partial}{\partial t} G(t,t’) = \delta(t – t’),
\end{equation}
then we have solved the system. We can simplify this slightly by presuming that the \( t,t’ \) dependence is always a difference, and seek \( G(\tau) \) such that
\begin{equation}\label{eqn:greensDropWithResistance:380}
m G”(\tau) + \gamma G'(\tau) = \delta(\tau).
\end{equation}
We now pull the Fourier transform out of our toolbox again, assuming that
\begin{equation}\label{eqn:greensDropWithResistance:400}
G(\tau) = \inv{2 \pi} \int_{-\infty}^\infty \hat{G}(\omega) e^{i\omega\tau} d\omega,
\end{equation}
for which
\begin{equation}\label{eqn:greensDropWithResistance:420}
\inv{2 \pi} \int_{-\infty}^\infty \lr{ m \lr{ i \omega }^2 + \gamma \lr{ i \omega } } \hat{G}(\omega) e^{i\omega \tau} d\omega
=
\inv{2 \pi } \int_{-\infty}^\infty e^{i\omega \tau} d\omega,
\end{equation}
or
\begin{equation}\label{eqn:greensDropWithResistance:440}
\hat{G}(\omega) = \inv{ m \lr{ i \omega }^2 + \gamma \lr{ i \omega } }.
\end{equation}
This is the Fourier transform of the Green’s function, and is exactly what we found earlier using pure Fourier transforms. Our starting point was different this time, as we just blatantly assumed that the solution had a convolution structure. We then found a differential equation for that convolution kernel, the Green’s function. Only then did we pull the Fourier transform out of the toolbox to attempt to find the structure of that Green’s function.
Evaluating the Green’s function integral.
We can’t go any further without figuring out what to do with our nasty little divergent integral \ref{eqn:greensDropWithResistance:220}. We may coerce this into something that we can evaluate using standard contour integration, if we offset the pole at the origin slightly. Given \( \epsilon > 0 \), let’s evaluate
\begin{equation}\label{eqn:greensDropWithResistance:460}
G(\tau, \epsilon) = -\inv{2\pi} \oint \frac{ e^{i z \tau} }{\lr{ z – i \epsilon } \lr{ m z – i \gamma}} dz.
\end{equation}
We can evaluate this integral using infinite semicircular contours, using an upper half plane contour for \( \tau > 0 \) and a lower half plane contour for \( \tau < 0 \), as illustrated in fig. 1, and fig. 2.
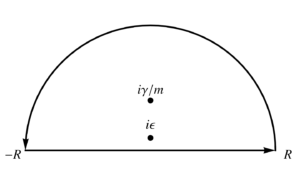
fig. 1. Contour for tau > 0.
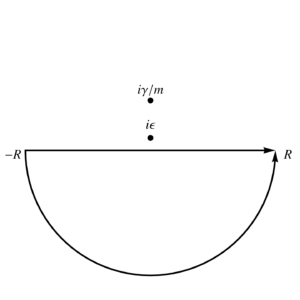
fig. 2. Contour for tau < 0.
By Jordan’s lemma, that upper half plane infinite semicircular part of the contour integral is zero for the \( \tau > 0 \) case, and for the \( \tau < 0 \) case, the lower half plane infinite semicircular part of the contour integral is zero. We can proceed with the residue calculations. In the upper half plane, we have both of the enclosed poles, so \begin{equation}\label{eqn:greensDropWithResistance:480} \begin{aligned} G(\tau > 0, \epsilon)
&= -\inv{2\pi m } \int_{-\infty}^\infty \frac{ e^{i \omega \tau} }{\lr{ \omega – i \epsilon } \lr{ \omega – i \gamma/m}} d\omega \\
&= -\frac{ 2 \pi i }{ 2 \pi m} \lr{
\evalbar{ \frac{ e^{i z \tau} }{ z – i \gamma/m} }{z = i \epsilon}
+
\evalbar{ \frac{ e^{i z \tau} }{ z – i \epsilon } }{ z = i \gamma/m}
} \\
&=
-\frac{i}{m} \lr{
\frac{ e^{-\epsilon \tau} }{ i \epsilon – i \gamma/m}
+
\frac{ e^{-\gamma\tau/m} }{ i \gamma/m – i \epsilon }
} \\
&=
-\lr{
\frac{e^{-\epsilon \tau}}{ m \epsilon – \gamma }
+
\frac{ e^{-\gamma\tau/m} }{ \gamma – m \epsilon }
},
\end{aligned}
\end{equation}
and for the lower half plane, where there are no enclosed poles we have \( G(\tau < 0, \epsilon) = 0 \). In the \( \epsilon \rightarrow 0 \) limit, we are left with
\begin{equation}\label{eqn:greensDropWithResistance:500}
G(\tau) = \inv{\gamma} \lr{ 1 – e^{-\gamma \tau/m} } \Theta(\tau).
\end{equation}
Back to the original problem.
We may now go and find the specific solution for the original problem where \( F(t) = – m g \Be_2 \Theta(t) \). That solution is
\begin{equation}\label{eqn:greensDropWithResistance:520}
\begin{aligned}
\Bx(t)
&= \Bx(0) + \int_{-\infty}^\infty G(t – t’) \lr{ – m g \Be_2 \Theta(t’) } dt’ \\
&= \Bx(0) – m g \Be_2 \int_{-\infty}^\infty \frac{\Theta(t – t’)}{\gamma} \lr{ 1 – e^{-\gamma \lr{ t – t’}/m } } \Theta(t’) dt’ \\
&= \Bx(0) – m g \Be_2 \int_{0}^\infty \frac{\Theta(t – t’)}{\gamma} \lr{ 1 – e^{-\gamma \lr{ t – t’}/m } } dt’ \\
&= \Bx(0) – \frac{m g}{\gamma} \Be_2 \int_{0}^t \lr{ 1 – e^{-\gamma \lr{ t – t’}/m } } dt’ \\
&= \Bx(0) – \frac{m g}{\gamma} \Be_2 \int_0^t \lr{ 1 – e^{-\gamma u/m } } du \\
&= \Bx(0) – \frac{m g}{\gamma} \Be_2 \evalrange{ \lr{ t’ – \frac{e^{-\gamma u/m } }{-\gamma/m} } }{u=0}{t} \\
&= \Bx(0) – \frac{m g}{\gamma} \Be_2 \lr{ t + \frac{m e^{-\gamma t/m }}{\gamma} – \frac{m}{\gamma} } \\
&= \Bx(0) – \frac{m g t}{\gamma} \Be_2 – \frac{m^2 g}{\gamma^2} \lr{ 1 – e^{-\gamma t/m } }.
\end{aligned}
\end{equation}
Ignoring the missing factor of \( g \) on the last term in the twitter slide, this is the final result before the limiting argument on that slide.
Having found the Green’s function for this system, we could then, fairly trivially, use it to solve similar systems with different forcing functions. For example, suppose we have a mass on a table, with friction, and a forcing function (perhaps sinusoidal) moving that mass. We could then figure out the time response for that particular forcing function, and would only have a convolution integral to evaluate. That general applicability is one of the beauties of these transform or Green’s function methods.
Like this:
Like Loading...