[Click here for a PDF version of this post]
On LinkedIn, James asked for ideas about how to solve What is the total area of ABC? You should be able to solve this! using geometric algebra.
I found one way, but suspect it’s not the easiest way to solve the problem.
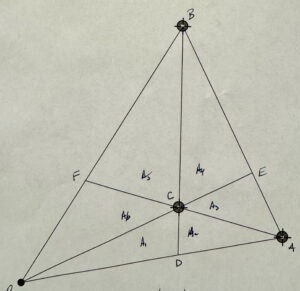
To start with I’ve re-sketched the triangle with the areas slightly more to scale in fig. 1, where areas \( A_1, A_2, A_3, A_5\) are given. The aim is to find the total area \( \sum A_i \).
If we had the vertex and center locations as vectors, we could easily compute the total area, but we don’t. We also don’t know the locations of the edge intersections, but can calculate those, as they satisfy
\begin{equation}\label{eqn:triangle_area_problem:20}
\begin{aligned}
\BD &= s_1 \BA = \BB + t_1 \lr{ \BC – \BB } \\
\BE &= s_2 \BC = \BA + t_2 \lr{ \BB – \BA } \\
\BF &= s_3 \BB = \BA + t_3 \lr{ \BC – \BA }.
\end{aligned}
\end{equation}
Eliminating the \( t_i \) constants by wedging appropriately (or equivalently, using Cramer’s rule), we find
\begin{equation}\label{eqn:triangle_area_problem:40}
\begin{aligned}
s_1 \BA \wedge \lr{ \BC – \BB } &= \BB \wedge \lr{ \BC – \BB } \\
s_2 \BC \wedge \lr{ \BB – \BA } &= \BA \wedge \lr{ \BB – \BA } \\
s_3 \BB \wedge \lr{ \BC – \BA } &= \BA \wedge \lr{ \BC – \BA },
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:triangle_area_problem:60}
\begin{aligned}
s_1 &= \frac{\BB \wedge \BC }{\BA \wedge \lr{ \BC – \BB }} \\
s_2 &= \frac{\BA \wedge \BB }{\BC \wedge \lr{ \BB – \BA }} \\
s_3 &= \frac{\BA \wedge \BC }{\BB \wedge \lr{ \BC – \BA }}.
\end{aligned}
\end{equation}
Introducing bivector (signed-area) unknowns
\begin{equation}\label{eqn:triangle_area_problem:80}
\begin{aligned}
\alpha &= \BA \wedge \BB = \begin{vmatrix} \BA & \BB \end{vmatrix} \Be_{12} \\
\beta &= \BB \wedge \BC = \begin{vmatrix} \BB & \BC \end{vmatrix} \Be_{12} \\
\gamma &= \BC \wedge \BA = \begin{vmatrix} \BC & \BA \end{vmatrix} \Be_{12}.
\end{aligned}
\end{equation}
the intersection parameters are
\begin{equation}\label{eqn:triangle_area_problem:100}
\begin{aligned}
s_1 &= \frac{\BB \wedge \BC }{\BA \wedge \BC – \BA \wedge \BB } = \frac{\beta}{-\gamma – \alpha} \\
s_2 &= \frac{\BA \wedge \BB }{\BC \wedge \BB – \BC \wedge \BA } = \frac{\alpha}{-\beta – \gamma} \\
s_3 &= \frac{\BA \wedge \BC }{\BB \wedge \BC – \BB \wedge \BA } = \frac{-\gamma}{\beta + \alpha},
\end{aligned}
\end{equation}
so the intersection points are
\begin{equation}\label{eqn:triangle_area_problem:120}
\begin{aligned}
\BD &= -\BA \frac{\beta}{\gamma + \alpha} \\
\BE &= -\BC \frac{\alpha}{\beta + \gamma} \\
\BF &= -\BB \frac{\gamma}{\beta + \alpha}.
\end{aligned}
\end{equation}
We may now express the known areas in terms of these unknown vectors
\begin{equation}\label{eqn:triangle_area_problem:140}
\begin{aligned}
A_1 &= \inv{2} \Abs{ \BD \wedge \BC } \\
A_2 &= \inv{2} \Abs{ \lr{\BC – \BA} \wedge \lr{ \BD – \BA } } \\
A_3 &= \inv{2} \Abs{ \lr{\BA – \BC} \wedge \lr{ \BE – \BC } } \\
A_5 &= \inv{2} \Abs{ \lr{\BB – \BC} \wedge \lr{ \BF – \BC } },
\end{aligned}
\end{equation}
but
\begin{equation}\label{eqn:triangle_area_problem:160}
\begin{aligned}
\BD – \BA &= -\BA \lr{ 1 + \frac{\beta}{\gamma + \alpha} } \\
\BE – \BC &= -\BC \lr{ 1 + \frac{\alpha}{\beta + \gamma} } \\
\BF – \BC &= -\BB \frac{\gamma}{\beta + \alpha} – \BC,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:triangle_area_problem:180}
\begin{aligned}
A_1 &= \inv{2} \Abs{ \BA \wedge \BC \frac{\beta}{\gamma + \alpha} } = \inv{2} \Abs{ \gamma} \Abs{ \frac{\beta}{\gamma + \alpha} } \\
A_2 &= \inv{2} \Abs{ \lr{\BC – \BA} \wedge \BA } \Abs{ 1 + \frac{\beta}{\gamma + \alpha} } = \inv{2} \Abs{\gamma} \Abs{ 1 + \frac{\beta}{\gamma + \alpha} } \\
A_3 &= \inv{2} \Abs{ \lr{\BA – \BC} \wedge \BC } \Abs{ 1 + \frac{\alpha}{\beta + \gamma} } = \inv{2} \Abs{\gamma} \Abs{ 1 + \frac{\alpha}{\beta + \gamma} },
\end{aligned}
\end{equation}
and
\begin{equation}\label{eqn:triangle_area_problem:200}
\begin{aligned}
A_5
&= \inv{2} \Abs{ \lr{\BB – \BC} \wedge \lr{ \BB \frac{\gamma}{\beta + \alpha} + \BC } } \\
&= \inv{2} \Abs{ \BB \wedge \BC – \BC \wedge \BB \frac{\gamma}{\beta + \alpha} } \\
&= \inv{2} \Abs{ \beta } \Abs{ 1 + \frac{\gamma}{\beta + \alpha} }.
\end{aligned}
\end{equation}
This gives us four equations in two (bivector) unknowns
\begin{equation}\label{eqn:triangle_area_problem:220}
\begin{aligned}
4 A_1^2 \lr{ \gamma + \alpha }^2 &= -\gamma^2 \beta^2 \\
4 A_2^2 \lr{ \gamma + \alpha }^2 &= -\gamma^2 \lr{ \alpha + \beta + \gamma }^2 \\
4 A_3^2 \lr{ \gamma + \beta }^2 &= -\gamma^2 \lr{ \alpha + \beta + \gamma }^2 \\
4 A_4^2 \lr{ \alpha + \beta }^2 &= -\beta^2 \lr{ \alpha + \beta + \gamma }^2.
\end{aligned}
\end{equation}
Let’s recast this in terms of area determinants, to eliminate the bivector variables in these equations. To do so, write
\begin{equation}\label{eqn:triangle_area_problem:240}
\begin{aligned}
X &= \begin{vmatrix} \BA & \BB \end{vmatrix} \\
Y &= \begin{vmatrix} \BB & \BC \end{vmatrix} \\
Z &= \begin{vmatrix} \BC & \BA \end{vmatrix}.
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:triangle_area_problem:300}
\begin{aligned}
4 A_1^2 \lr{ Z + X }^2 &= Z^2 Y^2 \\
4 A_2^2 \lr{ Z + X }^2 &= Z^2 \lr{ X + Y + Z }^2 \\
4 A_3^2 \lr{ Z + Y }^2 &= Z^2 \lr{ X + Y + Z }^2 \\
4 A_4^2 \lr{ X + Y }^2 &= Y^2 \lr{ X + Y + Z }^2.
\end{aligned}
\end{equation}
The goal is now to solve this system for \( X \). That solution (courtesy of Mathematica), for the numeric values in the original problem \( A_1 = 40, A_2 = 30, A_3 = 35, A_4 = 84 \), is:
\begin{equation}\label{eqn:triangle_area_problem:280}
\begin{aligned}
X &= \pm 630 \\
Y &= \mp 280 \\
Z &= \mp 140,
\end{aligned}
\end{equation}
so the total area is \( 315 \).
Now, I’ll have to watch the video and see how he solved it. I’d guess in a considerably simpler way.