[Click here for a PDF of this post with nicer formatting]
Disclaimer
Peeter’s lecture notes from class. These may be incoherent and rough.
These are notes for the UofT course ECE1505H, Convex Optimization, taught by Prof. Stark Draper, from [1].
Last time
- examples of sets: planes, half spaces, balls, ellipses, cone of positive semi-definite matrices
- generalized inequalities
- examples of convexity preserving operations
Today
- more examples of convexity preserving operations
- separating and supporting hyperplanes
- basic definitions of convex functions
- epigraphs, quasi-convexity, sublevel sets
- first and second order conditions for convexity of differentiable functions.
Operations that preserve convexity
If \( S_\alpha \) is convex \( \forall \alpha \in A \), then
\begin{equation}\label{eqn:convexOptimizationLecture5:40}
\cup_{\alpha \in A} S_\alpha,
\end{equation}
is convex.
Example:
\begin{equation}\label{eqn:convexOptimizationLecture5:60}
F(\Bx) = A \Bx + \Bb
\end{equation}
\begin{equation}\label{eqn:convexOptimizationLecture5:80}
\begin{aligned}
\Bx &\in \mathbb{R}^n \\
A &\in \mathbb{R}^{m \times n} \\
F &: \mathbb{R}^{n} \rightarrow \mathbb{R}^m \\
\Bb &\in \mathbb{R}^m
\end{aligned}
\end{equation}
- If \( S \in \mathbb{R}^n \) is convex, then\begin{equation}\label{eqn:convexOptimizationLecture5:100}
F(S) = \setlr{ F(\Bx) | \Bx \in S }
\end{equation}is convex if \( F \) is affine. - If \( S \in \mathbb{R}^m \) is convex, then\begin{equation}\label{eqn:convexOptimizationLecture5:120}
F^{-1}(S) = \setlr{ \Bx | F(\Bx) \in S }
\end{equation}is convex.
Example:
\begin{equation}\label{eqn:convexOptimizationLecture5:140}
\setlr{ \By | \By = A \Bx + \Bb, \Norm{\Bx} \le 1}
\end{equation}
is convex. Here \( A \Bx + \Bb \) is an affine function (\(F(\Bx)\). This is the image of a (convex) unit ball, through an affine map.
Earlier saw when defining ellipses
\begin{equation}\label{eqn:convexOptimizationLecture5:160}
\By = P^{1/2} \Bx + \Bx_c
\end{equation}
Example :
\begin{equation}\label{eqn:convexOptimizationLecture5:180}
\setlr{ \Bx | \Norm{ A \Bx + \Bb } \le 1 },
\end{equation}
is convex. This can be seen by writing
\begin{equation}\label{eqn:convexOptimizationLecture5:200}
\begin{aligned}
\setlr{ \Bx | \Norm{ A \Bx + \Bb } \le 1 }
&=
\setlr{ \Bx | \Norm{ F(\Bx) } \le 1 } \\
&=
\setlr{ \Bx | F(\Bx) \in \mathcal{B} },
\end{aligned}
\end{equation}
where \( \mathcal{B} = \setlr{ \By | \Norm{\By} \le 1 } \). This is the pre-image (under \(F()\)) of a unit norm ball.
Example:
\begin{equation}\label{eqn:convexOptimizationLecture5:220}
\setlr{ \Bx \in \mathbb{R}^n | x_1 A_1 + x_2 A_2 + \cdots x_n A_n \le \mathcal{B} }
\end{equation}
where \( A_i \in S^m \) and \( \mathcal{B} \in S^m \), and the inequality is a matrix inequality. This is a convex set. The constraint is a “linear matrix inequality” (LMI).
This has to do with an affine map:
\begin{equation}\label{eqn:convexOptimizationLecture5:240}
F(\Bx) = B – 1 x_1 A_1 – x_2 A_2 – \cdots x_n A_n \ge 0
\end{equation}
(positive semi-definite inequality). This is a mapping
\begin{equation}\label{eqn:convexOptimizationLecture5:480}
F : \mathbb{R}^n \rightarrow S^m,
\end{equation}
since all \( A_i \) and \( B \) are in \( S^m \).
This \( F(\Bx) = B – A(\Bx) \) is a constant and a factor linear in x, so is affine. Can be written
\begin{equation}\label{eqn:convexOptimizationLecture5:260}
\setlr{ \Bx | B – A(\Bx) \ge 0 }
=
\setlr{ \Bx | B – A(\Bx) \in S^m_{+} }
\end{equation}
This is a pre-image of a cone of PSD matrices, which is convex. Therefore, this is a convex set.
Separating hyperplanes
Theorem: Separating hyperplanes
If \( S, T \subseteq \mathbb{R}^n \) are convex and disjoint
i.e. \( S \cup T = 0\), then
there exists on \( \Ba \in \mathbb{R}^n \) \( \Ba \ne 0 \) and a \( \Bb \in \mathbb{R}^n \) such that
\begin{equation*}
\Ba^\T \Bx \ge \Bb \, \forall \Bx \in S
\end{equation*}
and
\begin{equation*}
\Ba^\T \Bx < \Bb \,\forall \Bx \in T.
\end{equation*}
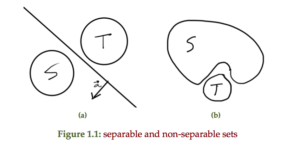
An example of a hyperplanes that separates two sets and two sets that are not separable is sketched in fig 1.1
Proof in the book.
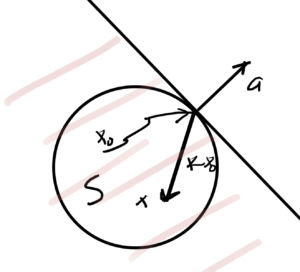
Theorem: Supporting hyperplane
If \( S \) is convex then \( \forall x_0 \in \partial S = \textrm{cl}(S) \ \textrm{int}(S) \), where
\( \partial S \) is the boundary of \( S \), then \( \exists \) an \( \Ba \ne 0 \in \mathbb{R}^n \) such that \( \Ba^\T \Bx \le \Ba^\T x_0 \, \forall \Bx \in S \).
Here \( \ \) denotes “without”.
An example is sketched in fig. 3, for which
- The vector \( \Ba \) perpendicular to tangent plane.
- inner product \( \Ba^\T (\Bx – \Bx_0) \le 0 \).
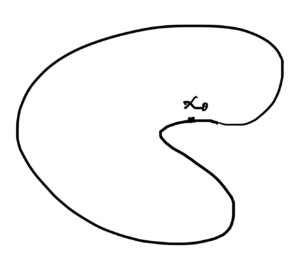
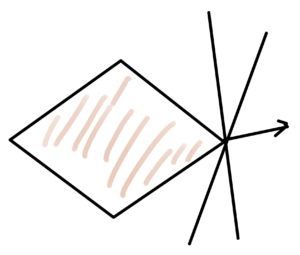
A set with a supporting hyperplane is sketched in fig 4a whereas fig 4b shows that there is not necessarily a unique supporting hyperplane at any given point, even if \( S \) is convex.
basic definitions of convex functions
Theorem: Convex functions
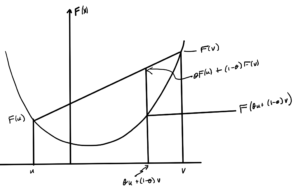
If \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) is defined on a convex domain (i.e. \( \textrm{dom} F \subseteq \mathbb{R}^n \) is a convex set), then \( F \) is convex if \( \forall \Bx, \By \in \textrm{dom} F \), \( \forall \theta \in [0,1] \in \mathbb{R} \)
\begin{equation}\label{eqn:convexOptimizationLecture5:340}
F( \theta \Bx + (1-\theta) \By \le \theta F(\Bx) + (1-\theta) F(\By)
\end{equation}
An example is sketched in fig. 5.
Remarks
- Require \( \textrm{dom} F \) to be a convex set. This is required so that the function at the point \( \theta u + (1-\theta) v \) can be evaluated. i.e. so that \( F(\theta u + (1-\theta) v) \) is well defined. Example: \( \textrm{dom} F = (-\infty, 0] \cup [1, \infty) \) is not okay, because a linear combination in \( (0,1) \) would be undesirable.
- Parameter \( \theta \) is “how much up” the line segment connecting \( (u, F(u) \) and \( (v, F(v) \). This line segment never below the bottom of the bowl.
The function is \underlineAndIndex{concave}, if \( -F \) is convex.
i.e. If the convex function is flipped upside down. That is\begin{equation}\label{eqn:convexOptimizationLecture5:360}
F(\theta \Bx + (1-\theta) \By ) \ge \theta F(\Bx) + (1-\theta) F(\By) \,\forall \Bx,\By \in \textrm{dom} F, \theta \in [0,1].
\end{equation} - a “strictly” convex function means \(\forall \theta \in [0,1] \)\begin{equation}\label{eqn:convexOptimizationLecture5:380}
F(\theta \Bx + (1-\theta) \By ) < \theta F(\Bx) + (1-theta) F(\By).
\end{equation} - Strictly concave function \( F \) means \( -F \) is strictly convex.
- Examples:\imageFigure{../figures/ece1505-convex-optimization/l5Fig6a}{}{fig:l5:l5Fig6a}{0.2}
Definition: Epigraph of a function
The epigraph \( \textrm{epi} F \) of a function \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) is
\begin{equation*}
\textrm{epi} F = \setlr{ (\Bx,t) \in \mathbb{R}^{n +1} | \Bx \in \textrm{dom} F, t \ge F(\Bx) },
\end{equation*}
where \( \Bx \in \mathbb{R}^n, t \in \mathbb{R} \).
Theorem: Convexity and epigraph.
If \( F \) is convex implies \( \textrm{epi} F \) is a convex set.
Proof:
For convex function, a line segment connecting any 2 points on function is above the function. i.e. it is \( \textrm{epi} F \).
Many authors will go the other way around, showing \ref{dfn:convexOptimizationLecture5:400} from \ref{thm:convexOptimizationLecture5:420}. That is:
Pick any 2 points in \( \textrm{epi} F \), \( (\Bx,\mu) \in \textrm{epi} F\) and \( (\By, \nu) \in \textrm{epi} F \). Consider convex combination
\begin{equation}\label{eqn:convexOptimizationLecture5:420}
\theta( \Bx, \mu ) + (1-\theta) (\By, \nu) =
(\theta \Bx (1-\theta) \By, \theta \mu (1-\theta) \nu )
\in \textrm{epi} F,
\end{equation}
since \( \textrm{epi} F \) is a convex set.
By definition of \( \textrm{epi} F \)
\begin{equation}\label{eqn:convexOptimizationLecture5:440}
F( \theta \Bx (1-\theta) \By ) \le \theta \mu (1-\theta) \nu.
\end{equation}
Picking \( \mu = F(\Bx), \nu = F(\By) \) gives
\begin{equation}\label{eqn:convexOptimizationLecture5:460}
F( \theta \Bx (1-\theta) \By ) \le \theta F(\Bx) (1-\theta) F(\By).
\end{equation}
Extended value function
Sometimes convenient to work with “extended value function”
\begin{equation}\label{eqn:convexOptimizationLecture5:500}
\tilde{F}(\Bx) =
\left\{
\begin{array}{l l}
F(\Bx) & \quad \mbox{If \( \Bx \in \textrm{dom} F\)} \\
\infty & \quad \mbox{otherwise.}
\end{array}
\right.
\end{equation}
Examples:
- Linear (affine) functions (fig. 8) are both convex and concave.
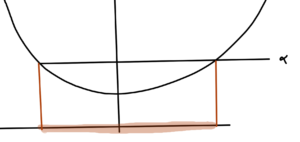
- \( x^2 \) is convex, sketched in fig. 9.
- \( \log x, \textrm{dom} F = \mathbb{R}_{+} \) concave, sketched in fig. 10.
- \( \Norm{\Bx} \) is convex. \( \Norm{ \theta \Bx + (1-\theta) \By } \le \theta \Norm{ \Bx } + (1-\theta) \Norm{\By } \).
- \( 1/x \) is convex on \( \setlr{ x | x > 0 } = \textrm{dom} F \), and concave on \( \setlr{ x | x < 0 } = \textrm{dom} F \). \begin{equation}\label{eqn:convexOptimizationLecture5:520} \tilde{F}(x) = \left\{ \begin{array}{l l} \inv{x} & \quad \mbox{If \( x > 0 \)} \\
\infty & \quad \mbox{else.}
\end{array}
\right.
\end{equation}
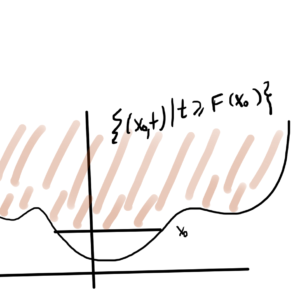
Definition: Sublevel
The sublevel set of a function \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) is
\begin{equation*}
C(\alpha) = \setlr{ \Bx \in \textrm{dom} F | F(\Bx) \le \alpha }
\end{equation*}
Theorem:
If \( F \) is convex then \( C(\alpha) \) is a convex set \( \forall \alpha \).
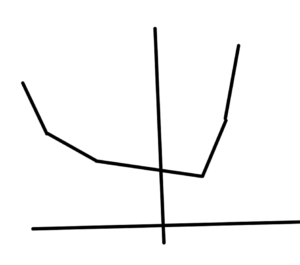
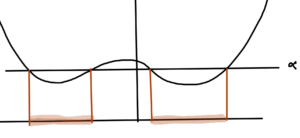
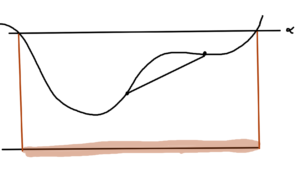
This is not an if and only if condition, as illustrated in fig. 12.
There \( C(\alpha) \) is convex, but the function itself is not.
Proof:
Since \( F \) is convex, then \( \textrm{epi} F \) is a convex set.
- Let\begin{equation}\label{eqn:convexOptimizationLecture5:580}
\mathcal{A} = \setlr{ (\Bx,t) | t = \alpha }
\end{equation}is a convex set. - \( \mathcal{A} \cap \textrm{epi} F \)is a convex set since it is the intersection of convex sets.
- Project \( \mathcal{A} \cap \textrm{epi} F \) onto \R{n} (i.e. domain of \( F \) ). The projection is an affine mapping. Image of a convex set through affine mapping is a convex set.
Definition: Quasi-convex.
A function is quasi-convex if \underline{all} of its sublevel sets are convex.
Composing convex functions
Properties of convex functions:
- If \( F \) is convex, then \( \alpha F \) is convex \( \forall \alpha > 0 \).
- If \( F_1, F_2 \) are convex, then the sum \( F_1 + F_2 \) is convex.
- If \( F \) is convex, then \( g(\Bx) = F(A \Bx + \Bb) \) is convex \( \forall \Bx \in \setlr{ \Bx | A \Bx + \Bb \in \textrm{dom} F } \).
Note: for the last
\begin{equation}\label{eqn:convexOptimizationLecture5:620}
\begin{aligned}
g &: \mathbb{R}^m \rightarrow \mathbb{R} \\
F &: \mathbb{R}^n \rightarrow \mathbb{R} \\
\Bx &\in \mathbb{R}^m \\
A &\in \mathbb{R}^{n \times m} \\
\Bb &\in \mathbb{R}^n
\end{aligned}
\end{equation}
Proof (of last):
\begin{equation}\label{eqn:convexOptimizationLecture5:640}
\begin{aligned}
g( \theta \Bx + (1-\theta) \By )
&=
F( \theta (A \Bx + \Bb) + (1-\theta) (A \By + \Bb) ) \\
&\le
\theta F( A \Bx + \Bb) + (1-\theta) F (A \By + \Bb) \\
&= \theta g(\Bx) + (1-\theta) g(\By).
\end{aligned}
\end{equation}
References
[1] Stephen Boyd and Lieven Vandenberghe. Convex optimization. Cambridge university press, 2004.