[Click here for a PDF version of this post]
Karl is taking his circuits course right now, which means that I get a chance to field some questions. I don’t get an excuse to think about this stuff any more. It’s fun material, since most of the ideas are all really simple, and you can figure out everything from first principles.
Karl just started sinusoidal circuits, which I think is a bit exciting. They are such a nice special case, as complex calculations are all effectively reduced to \( V = I R \) style computations.
Solving RLC circuits for general time dependent sources.
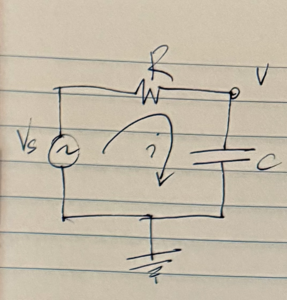
To contrast the simple case of sinusoidal sources, let’s consider what we have to do in order to solve a general case RLC circuit. The simple basic RC circuit sketched in fig. 1 provides a good illustrative example, even though it does not include any inductance.
With \( v \) as the voltage at the capacitor, the equations that describe the circuit are
\begin{equation}\label{eqn:impedance:20}
\begin{aligned}
v_s – v &= i R \\
i &= C \frac{dv}{dt}.
\end{aligned}
\end{equation}
We can combine these into one equation for \( v \). Letting \( \tau = RC \), that is
\begin{equation}\label{eqn:impedance:40}
v + \tau \frac{dv}{dt} = v_s.
\end{equation}
Here \( v_s = v_s(t) \) can be an arbitrary function of time. This is a simple enough differential equation, and can probably be solved in various ways (integrating factors, Fourier transforms, Laplace transforms, …)
For illustration purposes, let’s tackle this little equation with Fourier transforms, a method logically equivalent to the computation of the Green’s function for the system.
Let’s use a symmetric representation of the Fourier transform
\begin{equation}\label{eqn:impedance:60}
\begin{aligned}
F(\omega) &= \inv{\sqrt{2 \pi}} \int_{-\infty}^\infty e^{-j\omega t} f(t) dt \\
f(t) &= \inv{\sqrt{2 \pi}} \int_{-\infty}^\infty e^{j\omega t} F(\omega) d\omega \\
\end{aligned}
\end{equation}
Recall that the Fourier transform of the derivative is just a \( j \omega \) scaled frequency domain function, which we show with integration by parts
\begin{equation}\label{eqn:impedance:80}
\begin{aligned}
\inv{\sqrt{2 \pi}} \int_{-\infty}^\infty e^{-j\omega t} \frac{df}{dt} dt
&= \inv{\sqrt{2 \pi}} \int_{-\infty}^\infty \lr{ \frac{d}{dt} \lr{ f(t) e^{-j \omega t} } – f(t) \frac{d}{dt}\lr{ e^{-j\omega t}} } dt \\
&= j \omega F(\omega).
\end{aligned}
\end{equation}
That means that the frequency domain equivalent of our system is
\begin{equation}\label{eqn:impedance:100}
V + j \omega \tau V = V_s,
\end{equation}
or
\begin{equation}\label{eqn:impedance:120}
V(\omega) = \frac{V_s(\omega)}{1 + j \omega \tau}.
\end{equation}
Inverse transformation yields
\begin{equation}\label{eqn:impedance:140}
\begin{aligned}
v(t)
&= \inv{\sqrt{2 \pi}} \int_{-\infty}^\infty e^{j\omega t} \frac{V_s(\omega)}{1 + j \omega \tau} d\omega \\
&= \inv{2 \pi} \iint_{-\infty}^\infty e^{j\omega t} \frac{1}{1 + j \omega \tau} d\omega e^{-j\omega t’} v_s(t’) dt’ \\
&= \int_{-\infty}^\infty dt’ v_s(t’) \inv{2\pi} \int_{-\infty}^\infty \frac{e^{j\omega(t-t’)}}{1 + j \omega \tau} d\omega,
\end{aligned}
\end{equation}
or with
\begin{equation}\label{eqn:impedance:160}
G(u) = \inv{2\pi} \int_{-\infty}^\infty \frac{e^{j\omega u}}{1 + j \omega \tau} d\omega,
\end{equation}
\begin{equation}\label{eqn:impedance:180}
v(t) = \int_{-\infty}^\infty v_s(t’) G(t – t’) dt’.
\end{equation}
We just need to evaluate the Green’s function \( G(u) \) to proceed, which we can do with standard contour integration, first writing:
\begin{equation}\label{eqn:impedance:200}
\begin{aligned}
G(u)
&= \inv{2\pi j \tau} \int_{-\infty}^\infty \frac{e^{j\omega u}}{\inv{j\tau} + \omega} d\omega \\
&= \inv{2\pi j \tau} \oint \frac{e^{j z u}}{\inv{j\tau} + z} dz.
\end{aligned}
\end{equation}
This has a single pole at \( z = j/\tau \). We need an infinite semicircular contour in the lower half plane for \( u < 0 \), and can use the upper half plane infinite semicircular contour (surrounding the pole) for \( u > 0 \). That gives
\begin{equation}\label{eqn:impedance:220}
\begin{aligned}
G(u)
&= \Theta(u) \frac{2 \pi j}{2\pi j \tau} \evalbar{e^{j z u}}{z = j/\tau} \\
&= \frac{\Theta(u)}{\tau} e^{- u/\tau}.
\end{aligned}
\end{equation}
The solution to the problem, for any Fourier integrable source \( v_s(t) \), is
\begin{equation}\label{eqn:impedance:240}
\boxed{
v(t) = \int_{-\infty}^t v_s(t’) \frac{e^{- \lr{t – t’}/\tau}}{\tau} dt’.
}
\end{equation}
As a check, let’s evaluate this convolution integral for a step source \( v_s(t) = V \Theta(t) \), to find
\begin{equation}\label{eqn:impedance:260}
\begin{aligned}
v(t)
&= \frac{V e^{-t/tau}}{\tau} \int_0^t e^{t’/\tau} dt’ \\
&= V e^{-t/tau} \evalrange{e^{t’/\tau} }{0}{t} \\
&= V e^{-t/tau} \lr{ e^{t/\tau} – 1 } \\
&= V \lr{ 1 – e^{-t/\tau} }.
\end{aligned}
\end{equation}
This is the damped time domain response that we remember for an RC circuit. In Karl’s first year engineering notes, this was presented as a given (without the step factor), and he had to verify that it worked by differentiation (for \( t > 0 \).)
Solving this exactly, even for arbitrary sources, as we’ve done above, is not strictly hard, if you have all the required tools. But the first year engineering student doesn’t have all those tools to start with. This is where the beauty of the phasor techniques for sinusoidal sources comes in. Let’s now see how that works.
Phasor approach.
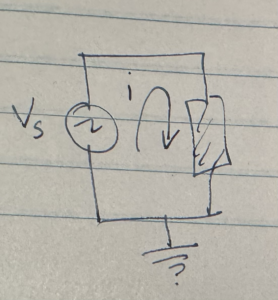
Let’s consider the three simplest RLC circuits, each with just a single element, and a variable voltage source. I’ll depict that element with a box as in fig. 2.
Resistor case.
If the element is a resistor with value \( R \), our equations are simple
\begin{equation}\label{eqn:impedance:280}
v_s = i R.
\end{equation}
Clearly \( i \) is directly proportional to the source voltage. In particular, if \( v_s(t) \) has a sinusoidal character, such as
\begin{equation}\label{eqn:impedance:300}
v_s(t) = V \cos(\omega t),
\end{equation}
then
\begin{equation}\label{eqn:impedance:320}
i(t) = \frac{V}{R} \cos\lr{ \omega t }.
\end{equation}
In particular, if we let \( i(t) = I \cos\lr{ \omega t } \), then we have
\begin{equation}\label{eqn:impedance:340}
I = \frac{V}{R},
\end{equation}
or \( V = I R \).
Capacitor case.
If the load element is a capacitor with capacitance \( C \), then the equation for the system is
\begin{equation}\label{eqn:impedance:360}
i = C \frac{dv_s(t)}{dt}.
\end{equation}
If we just plug in \( v_s(t) = V \cos(\omega t) \), as before, we get a bit of a mess
\begin{equation}\label{eqn:impedance:380}
i = -C \omega V \sin\lr{ \omega t }.
\end{equation}
We no longer have a nice simple proportionality relationship between the current and the voltage source, as the capacitor has introduced a phase shift into the mix.
We can figure out that phase factor by solving the equation
\begin{equation}\label{eqn:impedance:400}
-\sin x = \cos\lr{ x + \phi }.
\end{equation}
The easiest way to solve this is to express the sinusoids in complex exponential form
\begin{equation}\label{eqn:impedance:420}
\textrm{Re} \lr{ e^{j + \phi} } = \Real \lr{ j e^{j x} } = \Real \lr{ e^{j \pi/2} e^{j x} }.
\end{equation}
We see that the phase factor is a \( \pi/2 \) shift. However, even better, we have a strong hint that working with complex exponentials may be a better approach to formulating the problem.
Let’s write
\begin{equation}\label{eqn:impedance:440}
v_s(t) = V \cos\lr{ \omega t } = \textrm{Re} \lr{ V e^{j \omega t} }.
\end{equation}
Then we have
\begin{equation}\label{eqn:impedance:460}
i(t) = C V \textrm{Re} \lr{ \frac{d}{dt} e^{j \omega t} }.
\end{equation}
If we also assume that we can write
\begin{equation}\label{eqn:impedance:480}
i(t) = \textrm{Re} \lr{ I e^{j \omega t} },
\end{equation}
then if the real parts are equal, we must also have
\begin{equation}\label{eqn:impedance:500}
I e^{j \omega t} = j \omega C V e^{j \omega t},
\end{equation}
or
\begin{equation}\label{eqn:impedance:520}
I = j \omega C V.
\end{equation}
We have a \( V = I R \) relationship, which we write as
\begin{equation}\label{eqn:impedance:540}
V = I Z,
\end{equation}
where
\begin{equation}\label{eqn:impedance:560}
Z = \inv{j \omega C}.
\end{equation}
This is the phasor description of the circuit.
Inductive case.
If the circuit has an inductive load, then the system equation is
\begin{equation}\label{eqn:impedance:580}
v_s(t) = L \frac{di}{dt}.
\end{equation}
Again, we can write \( v_s(t) = \textrm{Re} \lr{ V e^{j\omega t} } \), and assume that \( i = \Real \lr{ I e^{j\omega t} } \). We then require
\begin{equation}\label{eqn:impedance:600}
V e^{j \omega t} = L \frac{d}{dt} \lr{ I e^{j \omega t} },
\end{equation}
or
\begin{equation}\label{eqn:impedance:620}
V = j \omega L I.
\end{equation}
We write
\begin{equation}\label{eqn:impedance:640}
Z = j \omega L,
\end{equation}
so once again \( V = I Z \).
Solving a more complex RLC configuration.
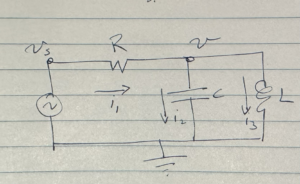
An example of a more complicated RLC circuit is sketched in fig. 3.
Here we have two impedances in parallel
\begin{equation}\label{eqn:impedance:660}
\begin{aligned}
Z_C &= \inv{j \omega C} \\
Z_L &= j \omega L.
\end{aligned}
\end{equation}
The parallel impedance through that reactive load is
\begin{equation}\label{eqn:impedance:680}
\begin{aligned}
Z
&= \lr{ \inv{Z_C} + \inv{Z_L} }^{-1} \\
&= \lr{ j \omega C + \inv{ j \omega L } }^{-1}.
\end{aligned}
\end{equation}
We can compute the current through \( R \) now
\begin{equation}\label{eqn:impedance:700}
I = \frac{V_s}{ R + \lr{ j \omega C + \inv{ j \omega L } }^{-1} }.
\end{equation}
We also have
\begin{equation}\label{eqn:impedance:720}
\frac{V_s – V}{R} = I,
\end{equation}
or
\begin{equation}\label{eqn:impedance:740}
\begin{aligned}
V
&= V_s – I R \\
&= V_s \lr{ 1 – \frac{R}{ R + \lr{ j \omega C + \inv{ j \omega L } }^{-1} } } \\
&= V_s \frac{\lr{ j \omega C + \inv{ j \omega L } }^{-1} }{ R + \lr{ j \omega C + \inv{ j \omega L } }^{-1} } \\
&= \frac{V_s}{ R \lr{ j \omega C + \inv{ j \omega L } } + 1 }.
\end{aligned}
\end{equation}
The complicated time response for this system is reduced to a trivial voltage divider calculation. We see that it was kind of pointless to run an inductor and capacitor in parallel, as they are both purely reactive (imaginary). That’s a detail that I didn’t remember, since it’s been decades since I did any practical circuits applications. However, the point is, by using a complex exponential source representation, these types of systems are reduced from systems of coupled differential equations to simple linear systems. Imagine how messy it would be to try to solve this system using the Green’s function methods that we used above!