variational method

Energy estimate for an absolute value potential

December 4, 2015 phy1520 , , ,

[Click here for a PDF of this post with nicer formatting]

Here’s a simple problem, a lot like the problem set 6 variational calculation.

Q: [1] 5.21

Estimate the lowest eigenvalue \( \lambda \) of the differential equation

\begin{equation}\label{eqn:absolutePotentialVariation:20}
\frac{d^2}{dx^2}\psi + \lr{ \lambda – \Abs{x} } \psi = 0.
\end{equation}

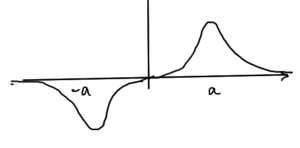
Using \( \alpha \) variation with the trial function

\begin{equation}\label{eqn:absolutePotentialVariation:40}
\psi =
\left\{
\begin{array}{l l}
c(\alpha – \Abs{x}) & \quad \mbox{\(\Abs{x} < \alpha \) } \\ 0 & \quad \mbox{\(\Abs{x} > \alpha \) }
\end{array}
\right.
\end{equation}

A:

First rewrite the differential equation in a Hamiltonian like fashion

\begin{equation}\label{eqn:absolutePotentialVariation:60}
H \psi = -\frac{d^2}{dx^2}\psi + \Abs{x} \psi = \lambda \psi.
\end{equation}

We need the derivatives of the trial distribution. The first derivative is

\begin{equation}\label{eqn:absolutePotentialVariation:80}
\begin{aligned}
\frac{d}{dx} \psi
&=
-c \frac{d}{dx} \Abs{x} \\
&=
-c \frac{d}{dx} \lr{ x \theta(x) – x \theta(-x) } \\
&=
-c \lr{
\theta(x) – \theta(-x)
+
x \delta(x) + x \delta(-x)
} \\
&=
-c \lr{
\theta(x) – \theta(-x)
+
2 x \delta(x)
}.
\end{aligned}
\end{equation}

The second derivative is
\begin{equation}\label{eqn:absolutePotentialVariation:100}
\begin{aligned}
\frac{d^2}{dx^2} \psi
&=
-c \frac{d}{dx} \lr{
\theta(x) – \theta(-x)
+
2 x \delta(x)
} \\
&=
-c \lr{
\delta(x) + \delta(-x)
+
2 \delta(x)
+
2 x \delta'(x)
} \\
&=
-c \lr{
4 \delta(x)
+
2 x \frac{-\delta(x) }{x}
} \\
&=
-2 c \delta(x).
\end{aligned}
\end{equation}

This gives

\begin{equation}\label{eqn:absolutePotentialVariation:120}
H \psi = -2 c \delta(x) + \Abs{x} c \lr{ \alpha – \Abs{x} }.
\end{equation}

We are now set to compute some of the inner products. The normalization is the simplest

\begin{equation}\label{eqn:absolutePotentialVariation:140}
\begin{aligned}
\braket{\psi}{\psi}
&= c^2 \int_{-\alpha}^\alpha ( \alpha – \Abs{x} )^2 dx \\
&= 2 c^2 \int_{0}^\alpha ( x – \alpha )^2 dx \\
&= 2 c^2 \int_{-\alpha}^0 u^2 du \\
&= 2 c^2 \lr{ -\frac{(-\alpha)^3}{3} } \\
&= \frac{2}{3} c^2 \alpha^3.
\end{aligned}
\end{equation}

For the energy
\begin{equation}\label{eqn:absolutePotentialVariation:160}
\begin{aligned}
\braket{\psi}{H \psi}
&=
c^2 \int dx \lr{ \alpha – \Abs{x} } \lr{ -2 \delta(x) + \Abs{x} \lr{ \alpha – \Abs{x} } } \\
&=
c^2 \lr{ – 2 \alpha + \int_{-\alpha}^\alpha dx \lr{ \alpha – \Abs{x} }^2 \Abs{x} } \\
&=
c^2 \lr{ – 2 \alpha + 2 \int_{-\alpha}^0 du u^2 \lr{ u + \alpha } } \\
&=
c^2 \lr{ – 2 \alpha + 2 \evalrange{\lr{ \frac{u^4}{4} + \alpha \frac{u^3}{3} }}{-\alpha}{0} } \\
&=
c^2 \lr{ – 2 \alpha – 2 \lr{ \frac{\alpha^4}{4} – \frac{\alpha^4}{3} } } \\
&=
c^2 \lr{ – 2 \alpha + \inv{6} \alpha^4 }.
\end{aligned}
\end{equation}

The energy estimate is

\begin{equation}\label{eqn:absolutePotentialVariation:180}
\begin{aligned}
\overline{{E}}
&=
\frac{\braket{\psi}{H \psi}}{\braket{\psi}{\psi}} \\
&=
\frac{ – 2 \alpha + \inv{6} \alpha^4 }{ \frac{2}{3} \alpha^3} \\
&=
– \frac{3}{\alpha^2} + \inv{4} \alpha.
\end{aligned}
\end{equation}

This has its minimum at
\begin{equation}\label{eqn:absolutePotentialVariation:200}
0 = -\frac{6}{\alpha^3} + \inv{4},
\end{equation}

or
\begin{equation}\label{eqn:absolutePotentialVariation:220}
\alpha = 2 \times 3^{1/3}.
\end{equation}

Back subst into the energy gives

\begin{equation}\label{eqn:absolutePotentialVariation:240}
\begin{aligned}
\overline{{E}}
&=
– \frac{3}{4 \times 3^{2/3}} + \inv{2} 3^{1/3} \\
&= \frac{3^{4/3}}{4} \\
&\approx 1.08.
\end{aligned}
\end{equation}

The problem says the exact answer is 1.019, so the variation gets within 6 %.

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

PHY1520H Graduate Quantum Mechanics. Lecture 19: Variational method. Taught by Prof. Arun Paramekanti

November 27, 2015 phy1520 , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course PHY1520, Graduate Quantum Mechanics, taught by Prof. Paramekanti, covering \textchapref{{5}} [1] content.

Variational method

Today we want to use the variational degree of freedom to try to solve some problems that we don’t have analytic solutions for.

Anharmonic oscillator

\begin{equation}\label{eqn:qmLecture19:20}
V(x) = \inv{2} m \omega^2 x^2 + \lambda x^4, \qquad \lambda \ge 0.
\end{equation}

With the potential growing faster than the harmonic oscillator, which had a ground state solution

\begin{equation}\label{eqn:qmLecture19:40}
\psi(x) = \inv{\pi^{1/4}} \inv{a_0^{1/2} } e^{- x^2/2 a_0^2},
\end{equation}

where
\begin{equation}\label{eqn:qmLecture19:60}
a_0 = \sqrt{\frac{\Hbar}{m \omega}}.
\end{equation}

Let’s try allowing \( a_0 \rightarrow a \), to be a variational degree of freedom

\begin{equation}\label{eqn:qmLecture19:80}
\psi_a(x) = \inv{\pi^{1/4}} \inv{a^{1/2} } e^{- x^2/2 a^2},
\end{equation}

\begin{equation}\label{eqn:qmLecture19:100}
\bra{\psi_a} H \ket{\psi_a}
=
\bra{\psi_a} \frac{p^2}{2m} + \inv{2} m \omega^2 x^2 + \lambda x^4 \ket{\psi_a}
\end{equation}

We can find
\begin{equation}\label{eqn:qmLecture19:120}
\expectation{x^2} = \inv{2} a^2
\end{equation}
\begin{equation}\label{eqn:qmLecture19:140}
\expectation{x^4} = \frac{3}{4} a^4
\end{equation}

Define

\begin{equation}\label{eqn:qmLecture19:160}
\tilde{\omega} = \frac{\Hbar}{m a^2},
\end{equation}

so that

\begin{equation}\label{eqn:qmLecture19:180}
\overline{{E}}_a
=
\bra{\psi_a} \lr{ \frac{p^2}{2m} + \inv{2} m \tilde{\omega}^2 x^2 }
+ \lr{
\inv{2} m \lr{ \omega^2 – \tilde{\omega}^2 } x^2
+
\lambda x^4 }
\ket{\psi_a}
=
\inv{2} \Hbar \tilde{\omega} + \inv{2} m \lr{ \omega^2 – \tilde{\omega}^2 } \inv{2} a^2 + \frac{3}{4} \lambda a^4.
\end{equation}

Write this as
\begin{equation}\label{eqn:qmLecture19:200}
\overline{{E}}_{\tilde{\omega}}
=
\inv{2} \Hbar \tilde{\omega} + \inv{4} \frac{\Hbar}{\tilde{\omega}} \lr{ \omega^2 – \tilde{\omega}^2 } + \frac{3}{4} \lambda \frac{\Hbar^2}{m^2 \tilde{\omega}^2 }.
\end{equation}

This might look something like fig. 1.

fig. 1: Energy after perturbation.

fig. 1: Energy after perturbation.

Demand that

\begin{equation}\label{eqn:qmLecture19:220}
0
= \PD{\tilde{\omega}}{ \overline{{E}}_{\tilde{\omega}}}
=
\frac{\Hbar}{2} – \frac{\Hbar}{4} \frac{\omega^2}{\tilde{\omega}^2}
– \frac{\Hbar}{4}
+ \frac{3}{4} (-2) \frac{\lambda \Hbar^2}{m^2 \tilde{\omega}^3}
=
\frac{\Hbar}{4}
\lr{
1 – \frac{\omega^2}{\tilde{\omega}^2}
– 6 \frac{\lambda \Hbar}{m^2 \tilde{\omega}^3}
}
\end{equation}

or
\begin{equation}\label{eqn:qmLecture19:260}
\tilde{\omega}^3 – \omega^2 \tilde{\omega} – \frac{6 \lambda \Hbar}{m^2} = 0.
\end{equation}

for \( \lambda a_0^4 \ll \Hbar \omega \), we have something like \( \tilde{\omega} = \omega + \epsilon \). Expanding \ref{eqn:qmLecture19:260} to first order in \( \epsilon \), this gives

\begin{equation}\label{eqn:qmLecture19:280}
\omega^3 + 3 \omega^2 \epsilon – \omega^2 \lr{ \omega + \epsilon } – \frac{6 \lambda \Hbar}{m^2} = 0,
\end{equation}

so that

\begin{equation}\label{eqn:qmLecture19:300}
2 \omega^2 \epsilon = \frac{6 \lambda \Hbar}{m^2},
\end{equation}

and

\begin{equation}\label{eqn:qmLecture19:320}
\Hbar \epsilon = \frac{ 3 \lambda \Hbar^2}{m^2 \omega^2 } = 3 \lambda a_0^4.
\end{equation}

Plugging into

\begin{equation}\label{eqn:qmLecture19:340}
\overline{{E}}_{\omega + \epsilon}
=
\inv{2} \Hbar \lr{ \omega + \epsilon }
+ \inv{4} \frac{\Hbar}{\omega} \lr{ -2 \omega \epsilon + \epsilon^2 } + \frac{3}{4} \lambda \frac{\Hbar^2}{m^2 \omega^2 }
\approx
\inv{2} \Hbar \lr{ \omega + \epsilon }
– \inv{2} \Hbar \epsilon
+ \frac{3}{4} \lambda \frac{\Hbar^2}{m^2 \omega^2 }
=
\inv{2} \Hbar \omega + \frac{3}{4} \lambda a_0^4.
\end{equation}

With \ref{eqn:qmLecture19:320}, that is

\begin{equation}\label{eqn:qmLecture19:540}
\overline{{E}}_{\tilde{\omega} = \omega + \epsilon} \approx \inv{2} \Hbar \lr{ \omega + \frac{\epsilon}{2} }.
\end{equation}

The energy levels are shifted slightly for each shift in the Hamiltonian frequency.

What do we have in the extreme anharmonic limit, where \( \lambda a_0^4 \gg \Hbar \omega \). Now we get

\begin{equation}\label{eqn:qmLecture19:360}
\tilde{\omega}^\conj = \lr{ \frac{ 6 \Hbar \lambda }{m^2} }^{1/3},
\end{equation}

and
\begin{equation}\label{eqn:qmLecture19:380}
\overline{{E}}_{\tilde{\omega}^\conj} = \frac{\Hbar^{4/3} \lambda^{1/3}}{m^{2/3}} \frac{3}{8} 6^{1/3}.
\end{equation}

(this last result is pulled from a web treatment somewhere of the anharmonic oscillator). Note that the first factor in this energy, with \( \Hbar^4 \lambda/m^2 \) traveling together could have been worked out on dimensional grounds.

This variational method tends to work quite well in these limits. For a system where \( m = \omega = \Hbar = 1 \), for this problem, we have

Capture

tab. 1: Comparing numeric and variational solutions.

Example: (sketch) double well potential

lecture19Fig2

fig. 2: Double well potential.

\begin{equation}\label{eqn:qmLecture19:400}
V(x) = \frac{m \omega^2}{8 a^2} \lr{ x – a }^2\lr{ x + a}^2.
\end{equation}

Note that this potential, and the Hamiltonian, both commute with parity.

We are interested in the regime where \( a_0^2 = \frac{\Hbar}{m \omega} \ll a^2 \).

Near \( x = \pm a \), this will be approximately

\begin{equation}\label{eqn:qmLecture19:420}
V(x) = \inv{2} m \omega^2 \lr{ x \pm a }^2.
\end{equation}

Guessing a wave function that is an eigenstate of parity

\begin{equation}\label{eqn:qmLecture19:440}
\Psi_{\pm} = g_{\pm} \lr{ \phi_{\textrm{R}}(x) \pm \phi_{\textrm{L}}(x) }.
\end{equation}

perhaps looking like the even and odd functions sketched in fig. 3, and fig. 4.

fig. 3. Even double well function

fig. 3. Even double well function

fig. 4. Odd double well function

fig. 4. Odd double well function

Using harmonic oscillator functions

\begin{equation}\label{eqn:qmLecture19:460}
\begin{aligned}
\phi_{\textrm{L}}(x) &= \Psi_{{\textrm{H}}.{\textrm{O}}.}(x + a) \\
\phi_{\textrm{R}}(x) &= \Psi_{{\textrm{H}}.{\textrm{O}}.}(x – a)
\end{aligned}
\end{equation}

After doing a lot of integral (i.e. in the problem set), we will see a splitting of the variational energy levels as sketched in fig. 5.

fig. 5. Splitting for double well potential.

fig. 5. Splitting for double well potential.

This sort of level splitting was what was used in the very first mazers.

Perturbation theory (outline)

Given

\begin{equation}\label{eqn:qmLecture19:480}
H = H_0 + \lambda V,
\end{equation}

where \( \lambda V \) is “small”. We want to figure out the eigenvalues and eigenstates of this Hamiltonian

\begin{equation}\label{eqn:qmLecture19:500}
H \ket{n} = E_n \ket{n}.
\end{equation}

We don’t know what these are, but do know that

\begin{equation}\label{eqn:qmLecture19:520}
H_0 \ket{n^{(0)}} = E_n^{(0)} \ket{n^{(0)}}.
\end{equation}

We are hoping that the level transitions have adiabatic transitions between the original and perturbed levels as sketched in fig. 6.

fig. 6. Adiabatic transitions.

fig. 6. Adiabatic transitions.

and not crossed level transitions as sketched in fig. 7.

fig. 7. Crossed level transitions.

fig. 7. Crossed level transitions.

If we have level crossings (which can in general occur), as opposed to adiabatic transitions, then we have no hope of using perturbation theory.

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

PHY1520H Graduate Quantum Mechanics. Lecture 18: Approximation methods. Taught by Prof. Arun Paramekanti

November 26, 2015 phy1520 , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough, especially since I didn’t attend this class myself, and am doing a walkthrough of notes provided by Nishant.

These are notes for the UofT course PHY1520, Graduate Quantum Mechanics, taught by Prof. Paramekanti, covering [1] chap. 5 content.

Approximation methods

Suppose we have a perturbed Hamiltonian

\begin{equation}\label{eqn:qmLecture18:20}
H = H_0 + \lambda V,
\end{equation}

where \( \lambda = 0 \) represents a solvable (perhaps known) system, and \( \lambda = 1 \) is the case of interest. There are two approaches of interest

  1. Direct solution of \( H \) with \( \lambda = 1 \).
  2. Take \( \lambda \) small, and do a series expansion. This is perturbation theory.

Variational methods

Given

\begin{equation}\label{eqn:qmLecture18:40}
H \ket{\phi_n} = E_n \ket{\phi_n},
\end{equation}

where we don’t know \( \ket{\phi_n} \), we can compute the expectation with respect to an arbitrary state \( \ket{\psi} \)

\begin{equation}\label{eqn:qmLecture18:60}
\bra{\psi} H \ket{\psi}
=
\bra{\psi} H \lr{ \sum_n \ket{\phi_n} \bra{\phi_n} } \ket{\psi}
=
\sum_n E_n \braket{\psi}{\phi_n} \braket{\phi_n}{\psi}
=
\sum_n E_n \Abs{\braket{\psi}{\phi_n}}^2.
\end{equation}

Define

\begin{equation}\label{eqn:qmLecture18:80}
\overline{{E}}
= \frac{\bra{\psi} H \ket{\psi}}{\braket{\psi}{\psi}}.
\end{equation}

Assuming that it is possible to express the state in the Hamiltonian energy basis

\begin{equation}\label{eqn:qmLecture18:100}
\ket{\psi}
=
\sum_n a_n \ket{\phi_n},
\end{equation}

this average energy is
\begin{equation}\label{eqn:qmLecture18:120}
\overline{{E}}
= \frac{ \sum_{m,n}\bra{\phi_m} a_m^\conj H a_n \ket{\phi_n}}{ \sum_n \Abs{a_n}^2 }
= \frac{ \sum_{n} \Abs{a_n}^2 E_n }{ \sum_n \Abs{a_n}^2 }.
= \sum_{n}
\frac{\Abs{a_n}^2 }{ \sum_n \Abs{a_n}^2 }
E_n
= \sum_n \frac{P_n}{\sum_m P_m} E_n,
\end{equation}

where \( P_m = \Abs{a_m}^2 \), which has the structure of a probability coefficient once divided by \( \sum_m P_m \), as sketched in fig. 1.

fig. 1. A decreasing probability distribution

fig. 1. A decreasing probability distribution

This average energy is a probability weighted average of the individual energy basis states. One of those energies is the ground state energy \( E_1 \), so we necessarily have

\begin{equation}\label{eqn:qmLecture18:140}
\boxed{
\overline{{E}} \ge E_1.
}
\end{equation}

Example: particle in a \( [0,L] \) box.

For the infinite potential box sketched in fig. 2.

fig. 2. Infinite potential [0,L] box.

fig. 2. Infinite potential [0,L] box.

The exact solutions for such a system are found to be

\begin{equation}\label{eqn:qmLecture18:220}
\psi(x) = \sqrt{\frac{2}{L}} \sin\lr{ \frac{n \pi}{L} x },
\end{equation}

where the energies are

\begin{equation}\label{eqn:qmLecture18:240}
E = \frac{\Hbar^2}{2m} \frac{n^2 \pi^2}{L^2}.
\end{equation}

The function \( \psi’ = x (L-x) \) also satisfies the boundary value constraints? How close in energy is that function to the ground state?

\begin{equation}\label{eqn:qmLecture18:260}
\overline{{E}}
=
-\frac{\Hbar^2}{2m} \frac{\int_0^L dx x (L-x) \frac{d^2}{dx^2} \lr{ x (L-x) }}{
\int_0^L dx x^2 (L-x)^2
}
=
\frac{\Hbar^2}{2m} \frac{\frac{2 L^3}{6}}{
\frac{L^5}{30}
}
=
\frac{\Hbar^2}{2m} \frac{10}{L^2}.
\end{equation}

This average energy is quite close to the ground state energy

\begin{equation}\label{eqn:qmLecture18:280}
\frac{\overline{{E}} }{E_1} = \frac{10}{\pi^2} = 1.014.
\end{equation}

Example II: particle in a \( [-L/2,L/2] \) box.

fig. 3. Infinite potential [-L/2,L/2] box.

fig. 3. Infinite potential [-L/2,L/2] box.

Shifting the boundaries, as sketched in fig. 3 doesn’t change the energy levels. For this potential let’s try a shifted trial function

\begin{equation}\label{eqn:qmLecture18:300}
\psi(x) = \lr{ x – \frac{L}{2} } \lr{ x + \frac{L}{2} } = x^2 – \frac{L^2}{4},
\end{equation}

without worrying about the form of the exact solution. This produces the same result as above

\begin{equation}\label{eqn:qmLecture18:270}
\overline{{E}}
=
-\frac{\Hbar^2}{2m} \frac{\int_0^L dx \lr{ x^2 – \frac{L^2}{4} } \frac{d^2}{dx^2} \lr{ x^2 – \frac{L^2}{4} }}{
\int_0^L dx \lr{x^2 – \frac{L^2}{4} }^2
}
=
-\frac{\Hbar^2}{2m} \frac{- 2 L^3/6}{
\frac{L^5}{30}
}
=
\frac{\Hbar^2}{2m} \frac{10}{L^2}.
\end{equation}

Summary (Nishant)

The above example is that of a particle in a box. The actual wave function is a sin as shown. But we can
come up with a guess wave function that meets the boundary conditions and ask how accurate it is
compared to the actual one.

Basically we are assuming a wave function form and then seeing how it differs from the exact form.
We cannot do this if we have nothing to compare it against. But, we note that the variance of the
number operator in the systems eigenstate is zero. So we can still calculate the variance and try to
minimize it. This is one way of coming up with an approximate wave function. This does not necessarily
give the ground state wave function though. For this we need to minimize the energy itself.

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.