[Click here for a PDF of this post with nicer formatting]
Question: Free particle propagator ([1] pr. 2.31)
Derive the free particle propagator in one and three dimensions.
Answer
I found the description in the text confusing, so let’s start from scratch with the definition of the propagator. This is the kernel of the spatial convolution integral that encodes time evolution, and can be expressed by expanding a general time state with two sets of identity operators. Let the position relative state at time \( t \), relative to an initial time \( t_0 \) be given by \( \braket{\Bx}{\alpha, t ; t_0 } \), and expand this in terms of a complete basis of energy eigenstates \( | a’ > \) and the time evolution operator
\begin{equation}\label{eqn:freeParticlePropagator:20}
\begin{aligned}
\braket{\Bx”}{\alpha, t ; t_0 }
&= \bra{\Bx”} U \ket{\alpha, t_0 } \\
&= \bra{\Bx”} e^{-i H (t -t_0)/\Hbar} \ket{\alpha, t_0 } \\
&= \bra{\Bx”} e^{-i H (t -t_0)/\Hbar} \lr{ \sum_{a’} \ket{a’} \bra{a’ }} \ket{\alpha, t_0 } \\
&= \bra{\Bx”} \sum_{a’} e^{-i E_{a’} (t -t_0)/\Hbar} \ket{a’} \braket{a’ }{\alpha, t_0 } \\
&=
\bra{\Bx”} \sum_{a’} e^{-i E_{a’} (t -t_0)/\Hbar} \ket{a’} \bra{a’ }
\lr{ \int d^3 \Bx’
\ket{\Bx’}\bra{\Bx’}
}
\ket{\alpha, t_0 } \\
&=
\int d^3 \Bx’
\lr{
\bra{\Bx”} \sum_{a’} e^{-i E_{a’} (t -t_0)/\Hbar} \ket{a’} \braket{a’ }{\Bx’}
}
\braket{\Bx’}{\alpha, t_0 } \\
&=
\int d^3 \Bx’ K(\Bx”, t ; \Bx’, t_0) \braket{\Bx’}{\alpha, t_0 },
\end{aligned}
\end{equation}
where
\begin{equation}\label{eqn:freeParticlePropagator:40}
K(\Bx”, t ; \Bx’, t_0) =
\sum_{a’}
\braket{\Bx”}{a’}\braket{a’ }{\Bx’}
e^{-i E_{a’} (t -t_0)/\Hbar},
\end{equation}
the propagator, is the kernel of the convolution integral that takes the state \( \ket{\alpha, t_0} \) to state \( \ket{\alpha, t ; t_0} \). Evaluating this over the momentum states (where integration and not plain summation is required), we have
\begin{equation}\label{eqn:freeParticlePropagator:60}
\begin{aligned}
K(\Bx”, t ; \Bx’, t_0)
&=
\int d^3 \Bp’
\braket{\Bx”}{\Bp’}\braket{\Bp’ }{\Bx’}
e^{-i E_{\Bp’} (t -t_0)/\Hbar} \\
&=
\int d^3 \Bp’
\braket{\Bx”}{\Bp’}\braket{\Bp’ }{\Bx’}
\exp\lr{-i \frac{(\Bp’)^2 (t -t_0)}{2 m \Hbar}} \\
&=
\int d^3 \Bp’
\frac{e^{i \Bx” \cdot \Bp’/\Hbar}}{(\sqrt{2 \pi \Hbar})^3}
\frac{e^{-i \Bx’ \cdot \Bp’/\Hbar}}{(\sqrt{2 \pi \Hbar})^3}
\exp\lr{-i \frac{(\Bp’)^2 (t -t_0)}{2 m \Hbar}} \\
&=
\inv{(2 \pi \Hbar)^3}
\int d^3 \Bp’
e^{i (\Bx” -\Bx’) \cdot \Bp’/\Hbar}
\exp\lr{-i \frac{(\Bp’)^2 (t -t_0)}{2 m \Hbar}} \\
&=
\inv{ 2 \pi \Hbar }
\int_{-\infty}^\infty dp_1′
e^{i (x_1” -x_1′) p_1’/\Hbar}
\exp\lr{-i \frac{(p_1′)^2 (t -t_0)}{2 m \Hbar}} \times \\
&\quad \inv{ 2 \pi \Hbar }
\int_{-\infty}^\infty dp_2′
e^{i (x_2” -x_2′) p_2’/\Hbar}
\exp\lr{-i \frac{(p_2′)^2 (t -t_0)}{2 m \Hbar}} \times \\
&\quad \inv{ 2 \pi \Hbar }
\int_{-\infty}^\infty dp_3′
e^{i (x_3” -x_3′) p_3’/\Hbar}
\exp\lr{-i \frac{(p_3′)^2 (t -t_0)}{2 m \Hbar}}
\end{aligned}
\end{equation}
With \( a = \ifrac{(t -t_0)}{2 m \Hbar} \), each of these three integral factors is of the form
\begin{equation}\label{eqn:freeParticlePropagator:80}
\begin{aligned}
\inv{ 2 \pi \Hbar }
\int_{-\infty}^\infty dp
e^{i \Delta x p/\Hbar }
\exp\lr{-i a p^2}
&=
\inv{2 \pi \Hbar \sqrt{a}}
\int_{-\infty}^\infty du
e^{i \Delta x u/(\sqrt{a}\Hbar) }
\exp\lr{-i u^2} \\
&=
\inv{2 \pi \Hbar \sqrt{a}}
\int_{-\infty}^\infty du
e^{i \Delta x u/(\sqrt{a} \Hbar) }
\exp\lr{-i (u – \Delta x /(2\sqrt{a}\Hbar))^2 + i(\Delta x/(2\sqrt{a}\Hbar))^2} \\
&=
\inv{2 \pi \Hbar \sqrt{a}}
\exp\lr{ \frac{i(\Delta x)^2 2 m \Hbar}{4 (t -t_0) \Hbar^2} }
\int_{-\infty}^\infty dz
e^{-i z^2} \\
&= \sqrt{ \frac{ -i \pi 2 m \Hbar}{ 4 \pi^2 \Hbar^2 (t -t_0)} }
\exp\lr{ \frac{i(\Delta x)^2 m}{2 (t -t_0) \Hbar} } \\
&= \sqrt{ \frac{ m }{ 2 \pi i \Hbar (t -t_0)} }
\exp\lr{ \frac{i(\Delta x)^2 m}{2 (t -t_0) \Hbar} }.
\end{aligned}
\end{equation}
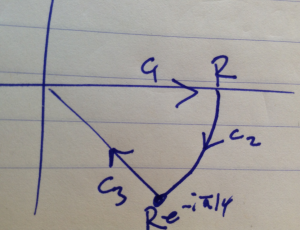
Note that the integral above has value \( \sqrt{-i\pi} \) which can be found by integrating over the contour of fig. 1, letting \( R \rightarrow \infty \).
Multiplying out each of the spatial direction factors gives the propagator in its closed form
\begin{equation}\label{eqn:freeParticlePropagator:120}
\boxed{
K(\Bx”, t ; \Bx’, t_0)
= \lr{ \sqrt{ \frac{ m }{ 2 \pi i \Hbar (t -t_0)} } }^3
\exp\lr{ \frac{i(\Bx” – \Bx’)^2 m}{2 (t -t_0) \Hbar} }.
}
\end{equation}
In one or two dimensions the exponential power \( 3 \) need only be adjusted appropriately.
Question: Momentum space free particle propagator ([1] pr. 2.33)
Derive the free particle propagator in momentum space.
Answer
The momentum space propagator follows in the same fashion as the spatial propagator
\begin{equation}\label{eqn:freeParticlePropagator:140}
\begin{aligned}
\braket{\Bp”}{\alpha, t ; t_0 }
&= \bra{\Bp”} U \ket{\alpha, t_0 } \\
&= \bra{\Bp”} e^{-i H (t -t_0)/\Hbar} \ket{\alpha, t_0 } \\
&= \bra{\Bp”} e^{-i H (t -t_0)/\Hbar} \lr{ \sum_{a’} \ket{a’} \bra{a’ }} \ket{\alpha, t_0 } \\
&= \bra{\Bp”} \sum_{a’} e^{-i E_{a’} (t -t_0)/\Hbar} \ket{a’} \braket{a’ }{\alpha, t_0 } \\
&=
\bra{\Bp”} \sum_{a’} e^{-i E_{a’} (t -t_0)/\Hbar} \ket{a’} \bra{a’ }
\lr{ \int d^3 \Bp’
\ket{\Bp’}\bra{\Bp’}
}
\ket{\alpha, t_0 } \\
&=
\int d^3 \Bp’
\lr{
\bra{\Bp”} \sum_{a’} e^{-i E_{a’} (t -t_0)/\Hbar} \ket{a’} \braket{a’ }{\Bp’}
}
\braket{\Bp’}{\alpha, t_0 } \\
&=
\int d^3 \Bp’ K(\Bp”, t ; \Bp’, t_0) \braket{\Bp’}{\alpha, t_0 },
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:freeParticlePropagator:160}
K(\Bp”, t ; \Bp’, t_0)
=
\sum_{a’}
\braket{\Bp”}{a’}
\braket{a’ }{\Bp’}
e^{-i E_{a’} (t -t_0)/\Hbar}.
\end{equation}
For the free particle Hamiltonian, this can be evaluated over a momentum space basis
\begin{equation}\label{eqn:freeParticlePropagator:170}
\begin{aligned}
K(\Bp”, t ; \Bp’, t_0)
&=
\int d^3 \Bp”’
\braket{\Bp”}{\Bp”’}
\braket{\Bp”’ }{\Bp’}
e^{-i E_{\Bp”’} (t -t_0)/\Hbar} \\
&=
\int d^3 \Bp”’
\braket{\Bp”}{\Bp”’}
\delta(\Bp”’ – \Bp’)
\exp\lr{ -i \frac{(\Bp”’)^2 (t -t_0)}{2 m \Hbar}} \\
&=
\braket{\Bp”}{\Bp’}
\exp\lr{ -i \frac{(\Bp’)^2 (t -t_0)}{2 m \Hbar}}
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:freeParticlePropagator:200}
\boxed{
K(\Bp”, t ; \Bp’, t_0)
=
\delta( \Bp” – \Bp’ )
\exp\lr{ -i \frac{(\Bp’)^2 (t -t_0)}{2 m \Hbar}}.
}
\end{equation}
This is what we expect since the time evolution is given by just this exponential factor
\begin{equation}\label{eqn:freeParticlePropagator:220}
\begin{aligned}
\braket{\Bp’}{\alpha, t_0 ; t}
&= \bra{\Bp’} \exp\lr{ -i \frac{(\Bp’)^2 (t -t_0)}{2 m \Hbar}} \ket{\alpha, t_0} \\
&=
\exp\lr{ -i \frac{(\Bp’)^2 (t -t_0)}{2 m \Hbar}}
\braket{\Bp’}
{\alpha, t_0}.
\end{aligned}
\end{equation}
References
[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.