[Click here for a PDF of this post with nicer formatting]
Given an alternate representation of the Dirac equation
\begin{equation}\label{eqn:diracAlternate:20}
H =
\begin{bmatrix}
m c^2 + V_0 & c \hat{p} \\
c \hat{p} & – m c^2 + V_0
\end{bmatrix},
\end{equation}
calculate the constant momentum solutions, the Heisenberg velocity operator \( \hat{v} \), and find the form of the probability density current.
Plane wave solutions
The action of the Hamiltonian on
\begin{equation}\label{eqn:diracAlternate:40}
\psi =
e^{i k x – i E t/\Hbar}
\begin{bmatrix}
\psi_1 \\
\psi_2
\end{bmatrix}
\end{equation}
is
\begin{equation}\label{eqn:diracAlternate:60}
\begin{aligned}
H \psi
&=
\begin{bmatrix}
m c^2 + V_0 & c (-i \Hbar) i k \\
c (-i \Hbar) i k & – m c^2 + V_0
\end{bmatrix}
\begin{bmatrix}
\psi_1 \\
\psi_2
\end{bmatrix}
e^{i k x – i E t/\Hbar} \\
&=
\begin{bmatrix}
m c^2 + V_0 & c \Hbar k \\
c \Hbar k & – m c^2 + V_0
\end{bmatrix}
\psi.
\end{aligned}
\end{equation}
Writing
\begin{equation}\label{eqn:diracAlternate:80}
H_k
=
\begin{bmatrix}
m c^2 + V_0 & c \Hbar k \\
c \Hbar k & – m c^2 + V_0
\end{bmatrix}
\end{equation}
the characteristic equation is
\begin{equation}\label{eqn:diracAlternate:100}
0
=
(m c^2 + V_0 – \lambda)
(-m c^2 + V_0 – \lambda)
– (c \Hbar k)^2
=
\lr{ (\lambda – V_0)^2 – (m c^2)^2 } – (c \Hbar k)^2,
\end{equation}
so
\begin{equation}\label{eqn:diracAlternate:120}
\lambda = V_0 \pm \epsilon,
\end{equation}
where
\begin{equation}\label{eqn:diracAlternate:140}
\epsilon^2 = (m c^2)^2 + (c \Hbar k)^2.
\end{equation}
We’ve got
\begin{equation}\label{eqn:diracAlternate:160}
\begin{aligned}
H – ( V_0 + \epsilon )
&=
\begin{bmatrix}
m c^2 – \epsilon & c \Hbar k \\
c \Hbar k & – m c^2 – \epsilon
\end{bmatrix} \\
H – ( V_0 – \epsilon )
&=
\begin{bmatrix}
m c^2 + \epsilon & c \Hbar k \\
c \Hbar k & – m c^2 + \epsilon
\end{bmatrix},
\end{aligned}
\end{equation}
so the eigenkets are
\begin{equation}\label{eqn:diracAlternate:180}
\begin{aligned}
\ket{V_0+\epsilon}
&\propto
\begin{bmatrix}
-c \Hbar k \\
m c^2 – \epsilon
\end{bmatrix} \\
\ket{V_0-\epsilon}
&\propto
\begin{bmatrix}
-c \Hbar k \\
m c^2 + \epsilon
\end{bmatrix}.
\end{aligned}
\end{equation}
Up to an arbitrary phase for each, these are
\begin{equation}\label{eqn:diracAlternate:200}
\begin{aligned}
\ket{V_0 + \epsilon}
&=
\inv{\sqrt{ 2 \epsilon ( \epsilon – m c^2) }}
\begin{bmatrix}
c \Hbar k \\
\epsilon -m c^2
\end{bmatrix} \\
\ket{V_0 – \epsilon}
&=
\inv{\sqrt{ 2 \epsilon ( \epsilon + m c^2) }}
\begin{bmatrix}
-c \Hbar k \\
\epsilon + m c^2
\end{bmatrix} \\
\end{aligned}
\end{equation}
We can now write
\begin{equation}\label{eqn:diracAlternate:220}
H_k =
E
\begin{bmatrix}
V_0 + \epsilon & 0 \\
0 & V_0 – \epsilon
\end{bmatrix}
E^{-1},
\end{equation}
where
\begin{equation}\label{eqn:diracAlternate:240}
\begin{aligned}
E &=
\inv{\sqrt{2 \epsilon} }
\begin{bmatrix}
\frac{c \Hbar k}{ \sqrt{ \epsilon – m c^2 } } & -\frac{c \Hbar k}{ \sqrt{ \epsilon + m c^2 } } \\
\sqrt{ \epsilon – m c^2 } & \sqrt{ \epsilon + m c^2 }
\end{bmatrix}, \qquad k > 0 \\
E &=
\inv{\sqrt{2 \epsilon} }
\begin{bmatrix}
-\frac{c \Hbar k}{ \sqrt{ \epsilon – m c^2 } } & -\frac{c \Hbar k}{ \sqrt{ \epsilon + m c^2 } } \\
-\sqrt{ \epsilon – m c^2 } & \sqrt{ \epsilon + m c^2 }
\end{bmatrix}, \qquad k < 0.
\end{aligned}
\end{equation}
Here the signs have been adjusted to ensure the transformation matrix has a unit determinant.
Observe that there's redundancy in this matrix since \( \ifrac{c \Hbar \Abs{k}}{ \sqrt{ \epsilon - m c^2 } } = \sqrt{ \epsilon + m c^2 } \), and \( \ifrac{c \Hbar \Abs{k}}{ \sqrt{ \epsilon + m c^2 } } = \sqrt{ \epsilon - m c^2 } \), which allows the transformation matrix to be written in the form of a rotation matrix
\begin{equation}\label{eqn:diracAlternate:260}
\begin{aligned}
E &=
\inv{\sqrt{2 \epsilon} }
\begin{bmatrix}
\frac{c \Hbar k}{ \sqrt{ \epsilon - m c^2 } } & -\frac{c \Hbar k}{ \sqrt{ \epsilon + m c^2 } } \\
\frac{c \Hbar k}{ \sqrt{ \epsilon + m c^2 } } & \frac{c \Hbar k}{ \sqrt{ \epsilon - m c^2 } }
\end{bmatrix}, \qquad k > 0 \\
E &=
\inv{\sqrt{2 \epsilon} }
\begin{bmatrix}
-\frac{c \Hbar k}{ \sqrt{ \epsilon – m c^2 } } & -\frac{c \Hbar k}{ \sqrt{ \epsilon + m c^2 } } \\
\frac{c \Hbar k}{ \sqrt{ \epsilon + m c^2 } } & -\frac{c \Hbar k}{ \sqrt{ \epsilon – m c^2 } }
\end{bmatrix}, \qquad k < 0 \\
\end{aligned}
\end{equation}
With
\begin{equation}\label{eqn:diracAlternate:280}
\begin{aligned}
\cos\theta &= \frac{c \Hbar \Abs{k}}{ \sqrt{ 2 \epsilon( \epsilon - m c^2) } } = \frac{\sqrt{ \epsilon + m c^2} }{ \sqrt{ 2 \epsilon}}\\
\sin\theta &= \frac{c \Hbar k}{ \sqrt{ 2 \epsilon( \epsilon + m c^2) } } = \frac{\textrm{sgn}(k) \sqrt{ \epsilon - m c^2}}{ \sqrt{ 2 \epsilon } },
\end{aligned}
\end{equation}
the transformation matrix (and eigenkets) is
\begin{equation}\label{eqn:diracAlternate:300}
\boxed{
E =
\begin{bmatrix}
\ket{V_0 + \epsilon} & \ket{V_0 - \epsilon}
\end{bmatrix}
=
\begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}.
}
\end{equation}
Observe that \ref{eqn:diracAlternate:280} can be simplified by using double angle formulas
\begin{equation}\label{eqn:diracAlternate:320}
\begin{aligned}
\cos(2 \theta)
&=
\frac{\lr{ \epsilon + m c^2} }{ 2 \epsilon }
-
\frac{\lr{ \epsilon - m c^2}}{ 2 \epsilon } \\
&=
\frac{1}{ 2 \epsilon } \lr{ \epsilon + m c^2 - \epsilon + m c^2 } \\
&=
\frac{m c^2 }{ \epsilon },
\end{aligned}
\end{equation}
and
\begin{equation}\label{eqn:diracAlternate:340}
\sin(2\theta)
=
2 \frac{1}{2 \epsilon} \textrm{sgn}(k ) \sqrt{ \epsilon^2 - (m c^2)^2 }
=
\frac{\Hbar k c}{\epsilon}.
\end{equation}
This allows all the \( \theta \) dependence on \( \Hbar k c \) and \( m c^2 \) to be expressed as a ratio of momenta
\begin{equation}\label{eqn:diracAlternate:360}
\boxed{
\tan(2\theta) = \frac{\Hbar k}{m c}.
}
\end{equation}
Hyperbolic solutions
For a wave function of the form
\begin{equation}\label{eqn:diracAlternate:380}
\psi =
e^{k x – i E t/\Hbar}
\begin{bmatrix}
\psi_1 \\
\psi_2
\end{bmatrix},
\end{equation}
some of the work above can be recycled if we substitute \( k \rightarrow -i k \), which yields unnormalized eigenfunctions
\begin{equation}\label{eqn:diracAlternate:400}
\begin{aligned}
\ket{V_0+\epsilon}
&\propto
\begin{bmatrix}
i c \Hbar k \\
m c^2 – \epsilon
\end{bmatrix} \\
\ket{V_0-\epsilon}
&\propto
\begin{bmatrix}
i c \Hbar k \\
m c^2 + \epsilon
\end{bmatrix},
\end{aligned}
\end{equation}
where
\begin{equation}\label{eqn:diracAlternate:420}
\epsilon^2 = (m c^2)^2 – (c \Hbar k)^2.
\end{equation}
The squared magnitude of these wavefunctions are
\begin{equation}\label{eqn:diracAlternate:440}
\begin{aligned}
(c \Hbar k)^2 + (m c^2 \mp \epsilon)^2
&=
(c \Hbar k)^2 + (m c^2)^2 + \epsilon^2 \mp 2 m c^2 \epsilon \\
&=
(c \Hbar k)^2 + (m c^2)^2 + (m c^2)^2 \mp (c \Hbar k)^2 – 2 m c^2 \epsilon \\
&= 2 (m c^2)^2 \mp 2 m c^2 \epsilon \\
&= 2 m c^2 ( m c^2 \mp \epsilon ),
\end{aligned}
\end{equation}
so, up to a constant phase for each, the normalized kets are
\begin{equation}\label{eqn:diracAlternate:460}
\begin{aligned}
\ket{V_0+\epsilon}
&=
\inv{\sqrt{ 2 m c^2 ( m c^2 – \epsilon ) }}
\begin{bmatrix}
i c \Hbar k \\
m c^2 – \epsilon
\end{bmatrix} \\
\ket{V_0-\epsilon}
&=
\inv{\sqrt{ 2 m c^2 ( m c^2 + \epsilon ) }}
\begin{bmatrix}
i c \Hbar k \\
m c^2 + \epsilon
\end{bmatrix},
\end{aligned}
\end{equation}
After the \( k \rightarrow -i k \) substitution, \( H_k \) is not Hermitian, so these kets aren’t expected to be orthonormal, which is readily verified
\begin{equation}\label{eqn:diracAlternate:480}
\begin{aligned}
\braket{V_0+\epsilon}{V_0-\epsilon}
&=
\inv{\sqrt{ 2 m c^2 ( m c^2 – \epsilon ) }}
\inv{\sqrt{ 2 m c^2 ( m c^2 + \epsilon ) }}
\begin{bmatrix}
-i c \Hbar k &
m c^2 – \epsilon
\end{bmatrix}
\begin{bmatrix}
i c \Hbar k \\
m c^2 + \epsilon
\end{bmatrix} \\
&=
\frac{ 2 ( c \Hbar k )^2 }{2 m c^2 \sqrt{(\Hbar k c)^2} } \\
&=
\textrm{sgn}(k)
\frac{
\Hbar k }{m c } .
\end{aligned}
\end{equation}
Heisenberg velocity operator
\begin{equation}\label{eqn:diracAlternate:500}
\begin{aligned}
\hat{v}
&= \inv{i \Hbar} \antisymmetric{ \hat{x} }{ H} \\
&= \inv{i \Hbar} \antisymmetric{ \hat{x} }{ m c^2 \sigma_z + V_0 + c \hat{p} \sigma_x } \\
&= \frac{c \sigma_x}{i \Hbar} \antisymmetric{ \hat{x} }{ \hat{p} } \\
&= c \sigma_x.
\end{aligned}
\end{equation}
Probability current
Acting against a completely general wavefunction the Hamiltonian action \( H \psi \) is
\begin{equation}\label{eqn:diracAlternate:520}
\begin{aligned}
i \Hbar \PD{t}{\psi}
&= m c^2 \sigma_z \psi + V_0 \psi + c \hat{p} \sigma_x \psi \\
&= m c^2 \sigma_z \psi + V_0 \psi -i \Hbar c \sigma_x \PD{x}{\psi}.
\end{aligned}
\end{equation}
Conversely, the conjugate \( (H \psi)^\dagger \) is
\begin{equation}\label{eqn:diracAlternate:540}
-i \Hbar \PD{t}{\psi^\dagger}
= m c^2 \psi^\dagger \sigma_z + V_0 \psi^\dagger +i \Hbar c \PD{x}{\psi^\dagger} \sigma_x.
\end{equation}
These give
\begin{equation}\label{eqn:diracAlternate:560}
\begin{aligned}
i \Hbar \psi^\dagger \PD{t}{\psi}
&=
m c^2 \psi^\dagger \sigma_z \psi + V_0 \psi^\dagger \psi -i \Hbar c \psi^\dagger \sigma_x \PD{x}{\psi} \\
-i \Hbar \PD{t}{\psi^\dagger} \psi
&= m c^2 \psi^\dagger \sigma_z \psi + V_0 \psi^\dagger \psi +i \Hbar c \PD{x}{\psi^\dagger} \sigma_x \psi.
\end{aligned}
\end{equation}
Taking differences
\begin{equation}\label{eqn:diracAlternate:580}
\psi^\dagger \PD{t}{\psi} + \PD{t}{\psi^\dagger} \psi
=
– c \psi^\dagger \sigma_x \PD{x}{\psi} – c \PD{x}{\psi^\dagger} \sigma_x \psi,
\end{equation}
or
\begin{equation}\label{eqn:diracAlternate:600}
0
=
\PD{t}{}
\lr{
\psi^\dagger \psi
}
+
\PD{x}{}
\lr{
c \psi^\dagger \sigma_x \psi
}.
\end{equation}
The probability current still has the usual form \( \rho = \psi^\dagger \psi = \psi_1^\conj \psi_1 + \psi_2^\conj \psi_2 \), but the probability current with this representation of the Dirac Hamiltonian is
\begin{equation}\label{eqn:diracAlternate:620}
\begin{aligned}
j
&= c \psi^\dagger \sigma_x \psi \\
&= c
\begin{bmatrix}
\psi_1^\conj &
\psi_2^\conj
\end{bmatrix}
\begin{bmatrix}
\psi_2 \\
\psi_1
\end{bmatrix} \\
&= c \lr{ \psi_1^\conj \psi_2 + \psi_2^\conj \psi_1 }.
\end{aligned}
\end{equation}
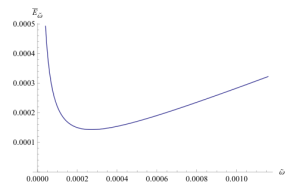
![fig. 2. Infinite potential [0,L] box.](https://peeterjoot.com/wp-content/uploads/2015/11/lecture18Fig2-300x271.png)
![fig. 3. Infinite potential [-L/2,L/2] box.](https://peeterjoot.com/wp-content/uploads/2015/11/lecture18Fig3-300x243.png)