February 19, 2019 Uncategorized
I’ve posted a minor update (tweaking some of the figures) of my PDF notes from electromagnetic theory (ECE1228H), such as they are. You can also find links to Mathematica notebooks, and instructions for cloning the git repositories to build the PDF.
Despite my love of the subject, this course was mediocre, and I’d rate my notes for it the same way.
February 9, 2019 Uncategorized
I’ve updated the pdf for my old phy450 notes (Relativistic Electrodynamics) from the current latex sources. Also included on that page are a contents listing, and instructions for forking the git repos. That should allow for building the pdf from the latex, so if somebody had changes they’d like to make, either for themselves or as feedback, they should be able to do so.
October 31, 2018 Uncategorized interaction, Perturbation ground state, time evolution operator, time ordered product
[Click here for a PDF of this post with nicer formatting]
These are notes for the UofT course PHY2403H, Quantum Field Theory, taught by Prof. Erich Poppitz, fall 2018.
We developed the interaction picture representation, which is really the Heisenberg picture with respect to \( H_0 \).
Recall that we found
\begin{equation}\label{eqn:qftLecture15:20}
U(t, t’) = e^{i H_0(t – t_0)} e^{-i H(t – t’)} e^{-i H_0(t’ – t_0)},
\end{equation}
with solution
\begin{equation}\label{eqn:qftLecture15:200}
U(t, t’)
=
T \exp{\lr{ -i \int_{t’}^t H_{\text{I,int}}(t”) dt”}},
\end{equation}
\begin{equation}\label{eqn:qftLecture15:220}
\begin{aligned}
U(t, t’)^\dagger
&=
T \exp{\lr{ i \int_{t’}^{t} H_{\text{I,int}}(t”) dt”}} \\
&=
T \exp{\lr{ -i \int_{t}^{t’} H_{\text{I,int}}(t”) dt”}} \\
&= U(t’, t),
\end{aligned}
\end{equation}
and can use this to calculate the time evolution of a field
\begin{equation}\label{eqn:qftLecture15:40}
\phi(\Bx, t)
=
U^\dagger(t, t_0)
\phi_I(\Bx, t)
U(t, t_0)
\end{equation}
and found the ground state ket for \( H \) was
\begin{equation}\label{eqn:qftLecture15:60}
\ket{\Omega}
=
\evalbar{
\frac{ U(t_0, -T) \ket{0} }
{
e^{-i E_0(T – t_0)} \braket{\Omega}{0}
}
}{T \rightarrow \infty(1 – i \epsilon)}.
\end{equation}
What’s the point of this, since it is self referential?
We will see, and also see that it goes away. Alternatively, you can write it as
\begin{equation*}
\ket{\Omega} \braket{\Omega}{0}
=
\evalbar{
\frac{ U(t_0, -T) \ket{0} }
{
e^{-i E_0(T – t_0)}
}
}{T \rightarrow \infty(1 – i \epsilon)}.
\end{equation*}
We can also show that
\begin{equation}\label{eqn:qftLecture15:80}
\bra{\Omega}
=
\evalbar{
\frac{ \bra{0} U(T, t_0) }
{
e^{-i E_0(T – t_0)} \braket{0}{\Omega}
}
}{T \rightarrow \infty(1 – i \epsilon)}.
\end{equation}
Our goal is still toe calculate
\begin{equation}\label{eqn:qftLecture15:100}
\bra{\Omega} T \phi(x) \phi(y) \ket{\Omega}.
\end{equation}
Claim: the “LSZ” theorem (a neat way of writing this) relates this to S matrix elements.
Assuming \( x^0 > y^0 \)
\begin{equation}\label{eqn:qftLecture15:120}
\bra{\Omega} \phi(x) \phi(y) \ket{\Omega}
=
\frac{
\bra{0}
U(T, t_0)
U^\dagger(x^0, t^0)
\phi_I(x)
U(x^0, t^0)
U^\dagger(y^0, t^0)
\phi_I(y)
U(y^0, t^0)
U(t_0, -T)
\ket{0}
}
{
e^{-i 2 E_0 T} \Abs{\braket{0}{\Omega}}^2
}
\end{equation}
Normalize \( \braket{\Omega}{\Omega} = 1 \), gives
\begin{equation}\label{eqn:qftLecture15:140}
\begin{aligned}
1
&=
\frac{\bra{0} U(T, t_0) U(t_0, -T) \ket{0}}
{
e^{-i 2 E_0 T} \Abs{\braket{0}{\Omega}}^2
} \\
&=
\frac{\bra{0} U(T, -T) \ket{0}}
{
e^{-i 2 E_0 T} \Abs{\braket{0}{\Omega}}^2
},
\end{aligned}
\end{equation}
so that
\begin{equation}\label{eqn:qftLecture15:240}
\bra{\Omega} \phi(x) \phi(y) \ket{\Omega}
=
\frac{
\bra{0}
U(T, t_0)
U^\dagger(x^0, t^0)
\phi_I(x)
U(x^0, t^0)
U^\dagger(y^0, t^0)
\phi_I(y)
U(y^0, t^0)
U(t_0, -T)
\ket{0}
}
{
\bra{0} U(T, -T) \ket{0}
}
\end{equation}
For \( t_1 > t_2 > t_3 \)
\begin{equation}\label{eqn:qftLecture15:280}
\begin{aligned}
U(t_1, t_2) U(t_2, t_3)
&=
T e^{-i \int_{t_2}^{t_1} H_I}
T e^{-i \int_{t_3}^{t_2} H_I} \\
&=
T \lr{
e^{-i \int_{t_2}^{t_1} H_I}
e^{-i \int_{t_3}^{t_2} H_I}
} \\
&=
T(
e^{-i \int_{t_3}^{t_1} H_I}
),
\end{aligned}
\end{equation}
with an end result of
\begin{equation}\label{eqn:qftLecture15:320}
U(t_1, t_2) U(t_2, t_3) = U(t_1, t_3).
\end{equation}
(DIY: work through the details — this is a problem in [1])
This gives
\begin{equation}\label{eqn:qftLecture15:300}
\bra{\Omega} \phi(x) \phi(y) \ket{\Omega}
=
\frac{
\bra{0}
U(T, x^0)
\phi_I(x)
U(x^0, y^0)
\phi_I(y)
U(y^0, -T)
\ket{0}
}
{
\bra{0} U(T, -T) \ket{0}
}.
\end{equation}
If \( y^0 > x^0 \) we have the same result, but the \( y \)’s will come first.
\begin{equation}\label{eqn:qftLecture15:340}
\bra{\Omega} \phi(x) \phi(y) \ket{\Omega}
=
\frac{
\bra{0}
T\lr{
\phi_I(x)
\phi_I(y)
e^{-i \int_{-T}^T H_{\text{I,int}}(t’) dt’}
}
\ket{0}
}
{
\bra{0}
T ( e^{-i \int_{-T}^T H_{\text{I,int}}(t’) dt’} )
\ket{0}
}.
\end{equation}
More generally
\begin{equation}\label{eqn:qftLecture15:360}
\boxed{
\bra{\Omega}
\phi_I(x_1) \cdots
\phi_I(x_n)
\ket{\Omega}
=
\frac{
\bra{0}
T\lr{
\phi_I(x_1) \cdots
\phi_I(x_n)
e^{-i \int_{-T}^T H_{\text{I,int}}(t’) dt’}
}
\ket{0}
}
{
\bra{0}
T ( e^{-i \int_{-T}^T H_{\text{I,int}}(t’) dt’} )
\ket{0}
}.
}
\end{equation}
This is the holy grail of perturbation theory.
In QFT II you will see this written in a path integral representation
\begin{equation}\label{eqn:qftLecture15:380}
\bra{\Omega}
\phi_I(x_1) \cdots
\phi_I(x_n)
\ket{\Omega}
=
\frac
{
\int [\mathcal{D} \phi] \phi(x_1) \phi(x_2) \cdots \phi(x_n) e^{-i S[\phi]}
}
{
\int [\mathcal{D} \phi] e^{-i S[\phi]}
}.
\end{equation}
\begin{equation}\label{eqn:qftLecture15:400}
\begin{aligned}
\int_{-T}^T H_{\text{I,int}}(t)
&=
\int_{-T}^T
\int d^3 \Bx \frac{\lambda}{4} \lr{ \phi_I(\Bx, t) }^4 \\
&=
\int d^4 x
\frac{\lambda}{4} \lr{ \phi_I }^4
\end{aligned}
\end{equation}
so we have
\begin{equation}\label{eqn:qftLecture15:420}
\frac{
\bra{0}
T\lr{
\phi_I(x_1) \cdots
\phi_I(x_n)
e^{-i \frac{\lambda}{4} \int d^4 x \phi_I^4(x) }
}
\ket{0}
}
{
\bra{0}
T
e^{-i \frac{\lambda}{4} \int d^4 x \phi_I^4(x) }
\ket{0}
}.
\end{equation}
The numerator expands as
\begin{equation}\label{eqn:qftLecture15:440}
\bra{0} T\lr{ \phi_I(x_1) \cdots \phi_I(x_n) } \ket{0}
-i \frac{\lambda}{4} \int d^4 x
\bra{0} T\lr{ \phi_I(x_1) \cdots \phi_I(x_n) \phi_I^4(x) }
+
\inv{2}
\lr{-i \frac{\lambda}{4}}^2 \int d^4 x d^4 y
\bra{0} T\lr{ \phi_I(x_1) \cdots \phi_I(x_n)
\phi_I^4(x)
\phi_I^4(y)
} \ket{0}
+ \cdots
\end{equation}
so we see that the problem ends up being the calculation of time ordered products.
Let’s simplify notation, dropping interaction picture suffixes, writing \( \phi(x_i) = \phi_i \).
Let’s calculate \(
\bra{0} T\lr{ \phi_1 \cdots \phi_n } \ket{0}
\). For \( n = 2 \) we have
\begin{equation}\label{eqn:qftLecture15:n}
\bra{0} T\lr{ \phi_1 \cdots \phi_n } \ket{0}
= D_F(x_1 – x_2) \equiv D_F(1-2)
\end{equation}
The rest of the lecture was very visual, and hard to type up. I’ll do so later.
[1] Michael E Peskin and Daniel V Schroeder. An introduction to Quantum Field Theory. Westview, 1995.
February 2, 2017 Uncategorized concave function, convex function, convex optimization, first order condition, gradient, Hessian, positive semi-definite, second order condition
[Click here for a PDF of this post with nicer formatting]
Peeter’s lecture notes from class. These may be incoherent and rough.
These are notes for the UofT course ECE1505H, Convex Optimization, taught by Prof. Stark Draper, from [1].
\begin{equation}\label{eqn:convexOptimizationLecture7:20}
\begin{aligned}
F(x) &= x^2 \\
F”(x) &= 2 > 0
\end{aligned}
\end{equation}
strictly convex.
\begin{equation}\label{eqn:convexOptimizationLecture7:40}
\begin{aligned}
F(x) &= x^3 \\
F”(x) &= 6 x.
\end{aligned}
\end{equation}
Not always non-negative, so not convex. However \( x^3 \) is convex on \( \textrm{dom} F = \mathbb{R}_{+} \).
\begin{equation}\label{eqn:convexOptimizationLecture7:60}
\begin{aligned}
F(x) &= x^\alpha \\
F'(x) &= \alpha x^{\alpha-1} \\
F”(x) &= \alpha(\alpha-1) x^{\alpha-2}.
\end{aligned}
\end{equation}
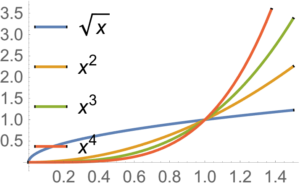
fig. 1. Powers of x.
This is convex on \( \mathbb{R}_{+} \), if \( \alpha \ge 1 \), or \( \alpha \le 0 \).
\begin{equation}\label{eqn:convexOptimizationLecture7:80}
\begin{aligned}
F(x) &= \log x \\
F'(x) &= \inv{x} \\
F”(x) &= -\inv{x^2} \le 0
\end{aligned}
\end{equation}
This is concave.
\begin{equation}\label{eqn:convexOptimizationLecture7:100}
\begin{aligned}
F(x) &= x\log x \\
F'(x) &= \log x + x \inv{x} = 1 + \log x \\
F”(x) &= \inv{x}
\end{aligned}
\end{equation}
This is strictly convex on
\( \mathbb{R}_{++} \), where
\( F”(x) \ge 0 \).
\begin{equation}\label{eqn:convexOptimizationLecture7:120}
\begin{aligned}
F(x) &= e^{\alpha x} \\
F'(x) &= \alpha e^{\alpha x} \\
F”(x) &= \alpha^2 e^{\alpha x} \ge 0
\end{aligned}
\end{equation}
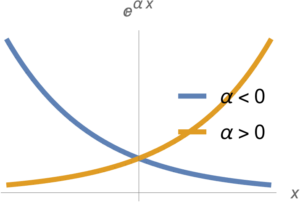
fig. 2. Exponential.
Such functions are plotted in fig. 2, and are convex function for all \( \alpha \).
For symmetric \( P \in S^n \)
\begin{equation}\label{eqn:convexOptimizationLecture7:140}
\begin{aligned}
F(\Bx) &= \Bx^\T P \Bx + 2 \Bq^\T \Bx + r \\
\spacegrad F &= (P + P^\T) \Bx + 2 \Bq = 2 P \Bx + 2 \Bq \\
\spacegrad^2 F &= 2 P.
\end{aligned}
\end{equation}
This is convex(concave) if \( P \ge 0 \) (\( P \le 0\)).
A quadratic function
\begin{equation}\label{eqn:convexOptimizationLecture7:780}
F(x, y) = x^2 + y^2 + 3 x y,
\end{equation}
that is neither convex nor concave is plotted in fig 3.
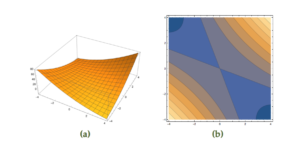
fig 3. Function with saddle point (3d and contours)
This function can be put in matrix form
\begin{equation}\label{eqn:convexOptimizationLecture7:160}
F(x, y) = x^2 + y^2 + 3 x y
=
\begin{bmatrix}
x & y
\end{bmatrix}
\begin{bmatrix}
1 & 1.5 \\
1.5 & 1
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix},
\end{equation}
and has the Hessian
\begin{equation}\label{eqn:convexOptimizationLecture7:180}
\begin{aligned}
\spacegrad^2 F
&=
\begin{bmatrix}
\partial_{xx} F & \partial_{xy} F \\
\partial_{yx} F & \partial_{yy} F \\
\end{bmatrix} \\
&=
\begin{bmatrix}
2 & 3 \\
3 & 2
\end{bmatrix} \\
&= 2 P.
\end{aligned}
\end{equation}
From the plot we know that this is not PSD, but this can be confirmed by checking the eigenvalues
\begin{equation}\label{eqn:convexOptimizationLecture7:200}
\begin{aligned}
0
&=
\det ( P – \lambda I ) \\
&=
(1 – \lambda)^2 – 1.5^2,
\end{aligned}
\end{equation}
which has solutions
\begin{equation}\label{eqn:convexOptimizationLecture7:220}
\lambda = 1 \pm \frac{3}{2} = \frac{3}{2}, -\frac{1}{2}.
\end{equation}
This is not PSD nor negative semi-definite, because it has one positive and one negative eigenvalues. This is neither convex nor concave.
Along \( y = -x \),
\begin{equation}\label{eqn:convexOptimizationLecture7:240}
\begin{aligned}
F(x,y)
&=
F(x,-x) \\
&=
2 x^2 – 3 x^2 \\
&=
– x^2,
\end{aligned}
\end{equation}
so it is concave along this line. Along \( y = x \)
\begin{equation}\label{eqn:convexOptimizationLecture7:260}
\begin{aligned}
F(x,y)
&=
F(x,x) \\
&=
2 x^2 + 3 x^2 \\
&=
5 x^2,
\end{aligned}
\end{equation}
so it is convex along this line.
\begin{equation}\label{eqn:convexOptimizationLecture7:280}
F(\Bx) = \sqrt{ x_1 x_2 },
\end{equation}
on \( \textrm{dom} F = \setlr{ x_1 \ge 0, x_2 \ge 0 } \)
For the Hessian
\begin{equation}\label{eqn:convexOptimizationLecture7:300}
\begin{aligned}
\PD{x_1}{F} &= \frac{1}{2} x_1^{-1/2} x_2^{1/2} \\
\PD{x_2}{F} &= \frac{1}{2} x_2^{-1/2} x_1^{1/2}
\end{aligned}
\end{equation}
The Hessian components are
\begin{equation}\label{eqn:convexOptimizationLecture7:320}
\begin{aligned}
\PD{x_1}{} \PD{x_1}{F} &= -\frac{1}{4} x_1^{-3/2} x_2^{1/2} \\
\PD{x_1}{} \PD{x_2}{F} &= \frac{1}{4} x_2^{-1/2} x_1^{-1/2} \\
\PD{x_2}{} \PD{x_1}{F} &= \frac{1}{4} x_1^{-1/2} x_2^{-1/2} \\
\PD{x_2}{} \PD{x_2}{F} &= -\frac{1}{4} x_2^{-3/2} x_1^{1/2}
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:convexOptimizationLecture7:340}
\spacegrad^2 F
=
-\frac{\sqrt{x_1 x_2}}{4}
\begin{bmatrix}
\inv{x_1^2} & -\inv{x_1 x_2} \\
-\inv{x_1 x_2} & \inv{x_2^2}
\end{bmatrix}.
\end{equation}
Checking this for PSD against \( \Bv = (v_1, v_2) \), we have
\begin{equation}\label{eqn:convexOptimizationLecture7:360}
\begin{aligned}
\begin{bmatrix}
v_1 & v_2
\end{bmatrix}
\begin{bmatrix}
\inv{x_1^2} & -\inv{x_1 x_2} \\
-\inv{x_1 x_2} & \inv{x_2^2}
\end{bmatrix}
\begin{bmatrix}
v_1 \\ v_2
\end{bmatrix}
&=
\begin{bmatrix}
v_1 & v_2
\end{bmatrix}
\begin{bmatrix}
\inv{x_1^2} v_1 -\inv{x_1 x_2} v_2 \\
-\inv{x_1 x_2} v_1 + \inv{x_2^2} v_2
\end{bmatrix} \\
&=
\lr{ \inv{x_1^2} v_1 -\inv{x_1 x_2} v_2 } v_1 +
\lr{ -\inv{x_1 x_2} v_1 + \inv{x_2^2} v_2 } v_2
\\
&=
\inv{x_1^2} v_1^2
+ \inv{x_2^2} v_2^2
-2 \inv{x_1 x_2} v_1 v_2 \\
&=
\lr{
\frac{v_1}{x_1}
-\frac{v_2}{x_2}
}^2 \\
&\ge 0,
\end{aligned}
\end{equation}
so \( \spacegrad^2 F \le 0 \). This is a negative semi-definite function (concave). Observe that this check required checking PSD for all values of \( \Bx \).
This is an example of a more general result
\begin{equation}\label{eqn:convexOptimizationLecture7:380}
F(x) = \lr{ \prod_{i = 1}^n x_i }^{1/n},
\end{equation}
which is concave (prove on homework).
If \( F \) is differentiable in \R{n}, then check the curvature of the function along all lines. i.e. At all locations and in all directions.
If the Hessian is PSD at all \( \Bx \in \textrm{dom} F \), that is
\begin{equation}\label{eqn:convexOptimizationLecture7:400}
\spacegrad^2 F \ge 0 \, \forall \Bx \in \textrm{dom} F,
\end{equation}
then the function is convex.
Over \( \textrm{dom} F = \mathbb{R}^n \)
\begin{equation}\label{eqn:convexOptimizationLecture7:420}
F(\Bx) = \max_{i = 1}^n x_i
\end{equation}
i.e.
\begin{equation}\label{eqn:convexOptimizationLecture7:440}
\begin{aligned}
F((1,2) &= 2 \\
F((3,-1) &= 3
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:convexOptimizationLecture7:460}
F(\Bx) = \max_{i = 1}^n F_i(\Bx),
\end{equation}
where
\begin{equation}\label{eqn:convexOptimizationLecture7:480}
F_i(\Bx)
=
… ?
\end{equation}
max of a set of convex functions is a convex function.
\begin{equation}\label{eqn:convexOptimizationLecture7:500}
F(x) =
x_{[1]} +
x_{[2]} +
x_{[3]}
\end{equation}
where
\( x_{[k]} \) is the k-th largest number in the list
Write
\begin{equation}\label{eqn:convexOptimizationLecture7:520}
F(x) = \max x_i + x_j + x_k
\end{equation}
\begin{equation}\label{eqn:convexOptimizationLecture7:540}
(i,j,k) \in \binom{n}{3}
\end{equation}
For \( \Ba \in \mathbb{R}^n \) and \( b_i \in \mathbb{R} \)
\begin{equation}\label{eqn:convexOptimizationLecture7:560}
\begin{aligned}
F(\Bx)
&= \sum_{i = 1}^n \log( b_i – \Ba^\T \Bx )^{-1} \\
&= -\sum_{i = 1}^n \log( b_i – \Ba^\T \Bx )
\end{aligned}
\end{equation}
This \( b_i – \Ba^\T \Bx \) is an affine function of \( \Bx \) so it doesn’t affect convexity.
Since \( \log \) is concave, \( -\log \) is convex. Convex functions of affine function of \( \Bx \) is convex function of \( \Bx \).
\begin{equation}\label{eqn:convexOptimizationLecture7:580}
F(\Bx) = \sup_{\By \in C} \Norm{ \Bx – \By }
\end{equation}
fig. 3. Max length function
Here \( C \subseteq \mathbb{R}^n \) is not necessarily convex. We are using \( \sup \) here because the set \( C \) may be open. This function is the length of the line from \( \Bx \) to the point in \( C \) that is furthest from \( \Bx \).
\begin{equation}\label{eqn:convexOptimizationLecture7:600}
F(\Bx) = \inf_{\By \in C} \Norm{ \Bx – \By }.
\end{equation}
Min and max of two convex functions are plotted in fig. 4.
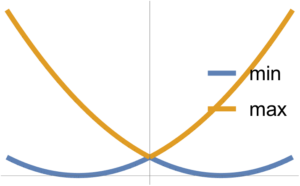
fig. 4. Min and max
The max is observed to be convex, whereas the min is not necessarily so.
\begin{equation}\label{eqn:convexOptimizationLecture7:800}
F(\Bz) = F(\theta \Bx + (1-\theta) \By) \ge \theta F(\Bx) + (1-\theta)F(\By).
\end{equation}
This is not necessarily convex for all sets \( C \subseteq \mathbb{R}^n \), because the \( \inf \) of a bunch of convex function is not necessarily convex. However, if \( C \) is convex, then \( F(\Bx) \) is convex.
If \( F \) is convex and one can find an \( \Bx^\conj \in \textrm{dom} F \) such that
\begin{equation}\label{eqn:convexOptimizationLecture7:640}
\spacegrad F(\Bx^\conj) = 0,
\end{equation}
then
\begin{equation}\label{eqn:convexOptimizationLecture7:660}
F(\By) \ge F(\Bx^\conj) \, \forall \By \in \textrm{dom} F.
\end{equation}
If you can find the point where the gradient is zero (which can’t always be found), then \( \Bx^\conj\) is a global minimum of \( F \).
Conversely, if \( \Bx^\conj \) is a global minimizer of \( F \), then \( \spacegrad F(\Bx^\conj) = 0 \) must hold. If that were not the case, then you would be able to find a direction to move downhill, contracting the optimality of \( \Bx^\conj\).
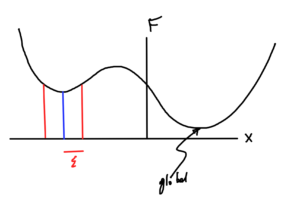
fig. 6. Global and local minimums
Definition: Local optimum
\( \Bx^\conj \) is a local optimum of \( F \) if \( \exists \epsilon > 0 \) such that \( \forall \Bx \), \( \Norm{\Bx – \Bx^\conj} < \epsilon \), we have
\begin{equation*}
F(\Bx^\conj) \le F(\Bx)
\end{equation*}
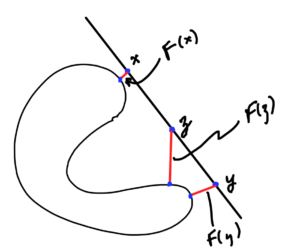
fig. 5. min length function
Theorem:
Suppose \( F \) is twice continuously differentiable (not necessarily convex)
Proof:
Here the fraction is \( \ge 0 \) since \( \Bx^\conj \) is a local optimum.
Since the choice of \( \Bv \) is arbitrary, the only case that you can ensure that \( \ge 0, \forall \Bv \) is
\begin{equation}\label{eqn:convexOptimizationLecture7:740}
\spacegrad F = 0,
\end{equation}
( or else could pick \( \Bv = -\spacegrad F(\Bx^\conj) \).
This means that \( \spacegrad F(\Bx^\conj) = 0 \) if \( \Bx^\conj \) is a local optimum.
Consider the 2nd order derivative
\begin{equation}\label{eqn:convexOptimizationLecture7:760}
\begin{aligned}
\lim_{t \rightarrow 0} \frac{ F(\Bx^\conj + t \Bv) – F(\Bx^\conj)}{t^2}
&=
\lim_{t \rightarrow 0} \inv{t^2}
\lr{
F(\Bx^\conj) + t \lr{ \spacegrad F(\Bx^\conj) }^\T \Bv + \inv{2} t^2 \Bv^\T \spacegrad^2 F(\Bx^\conj) \Bv + O(t^3)
– F(\Bx^\conj)
} \\
&=
\inv{2} \Bv^\T \spacegrad^2 F(\Bx^\conj) \Bv \\
&\ge 0.
\end{aligned}
\end{equation}
Here the \( \ge \) condition also comes from the fraction, based on the optimiality of \( \Bx^\conj \). This is true for all choice of \( \Bv \), thus \( \spacegrad^2 F(\Bx^\conj) \).
[1] Stephen Boyd and Lieven Vandenberghe. Convex optimization. Cambridge university press, 2004.
August 30, 2016 Uncategorized
I’ve just bought a nice new desk for my home office:
When I assembled the new desk, I took the opportunity to refine my home network setup. In this post I’ll walk through that setup.
I’ve got the router in the living room, along with the two NUC6i’s that I use for my lzlabs development work:
I run the NUCs headless, using ssh and command line access for my work. For those times that I need to refresh the install image and need a display, I also have them HDMI connected to the living room TV, and direct connected with short ethernet cables to the router:
The router is also directly connected to the PS3 (for netflix), and then runs through some ethernet lines that I fished into the basement, before some of the basement finishing work we did just after we moved in. All the lines I have going into the basement terminate in a patch panel:
Does a patch panel sound like overkill? Yes, it probably is. However, I’ve got a pile of roughed in ethernet lines to the kids rooms and the rec room that I’ll eventually fish into the electrical-panel/laundry/network room:
I’d like to also eventually fish some ethernet lines into the upstairs space (i.e. for netflix run off a blue-ray player that sits mostly unused in the master bedroom), but that’s a harder fishing job, and I haven’t done it yet. From the front of the patch panel things go off to the router:
and from there to a switch:
One line comes from the router (through the patch panel), and then all the rest of the ethernet lines from the switch go to final destinations. Four of those lines go back to the patch panel and up to the office space. One is plugged into one of the thunderbolt monitors, so I can use a wired connection while “docked”. One goes up to the office space and is connected to an Odroid (which can run the Lz stack on aarch64 hardware). One line goes back to the living room, for optional wired couch surfing, and the last is connected to a voip phone.
I’ve got a lot of finishing touches to do. I plan to mount the patch panel next to the electrical panel, instead of just placing it on top of the freezer down in the laundry room. I’ve also got lines that are running through the ceiling, but are hanging loose still. The wall panel in my office space is currently hanging loose:
I have a low voltage wiring box purchased, but need to cut the hole for it, so I can screw in this little panel and get it nicely out of the way, and do the plastering and painting to fix up the messy fishing holes I made trying to find a route down into the basement.