[Click here for a PDF of this post with nicer formatting]
Disclaimer
Peeter’s lecture notes from class. These may be incoherent and rough.
These are notes for the UofT course ECE1505H, Convex Optimization, taught by Prof. Stark Draper, from [1].
Today
- Local and global optimality
- Compositions of functions
- Examples
Example:
\begin{equation}\label{eqn:convexOptimizationLecture7:20}
\begin{aligned}
F(x) &= x^2 \\
F”(x) &= 2 > 0
\end{aligned}
\end{equation}
strictly convex.
Example:
\begin{equation}\label{eqn:convexOptimizationLecture7:40}
\begin{aligned}
F(x) &= x^3 \\
F”(x) &= 6 x.
\end{aligned}
\end{equation}
Not always non-negative, so not convex. However \( x^3 \) is convex on \( \textrm{dom} F = \mathbb{R}_{+} \).
Example:
\begin{equation}\label{eqn:convexOptimizationLecture7:60}
\begin{aligned}
F(x) &= x^\alpha \\
F'(x) &= \alpha x^{\alpha-1} \\
F”(x) &= \alpha(\alpha-1) x^{\alpha-2}.
\end{aligned}
\end{equation}
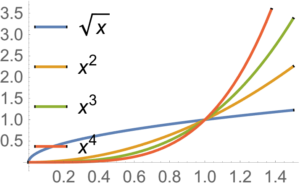
This is convex on \( \mathbb{R}_{+} \), if \( \alpha \ge 1 \), or \( \alpha \le 0 \).
Example:
\begin{equation}\label{eqn:convexOptimizationLecture7:80}
\begin{aligned}
F(x) &= \log x \\
F'(x) &= \inv{x} \\
F”(x) &= -\inv{x^2} \le 0
\end{aligned}
\end{equation}
This is concave.
Example:
\begin{equation}\label{eqn:convexOptimizationLecture7:100}
\begin{aligned}
F(x) &= x\log x \\
F'(x) &= \log x + x \inv{x} = 1 + \log x \\
F”(x) &= \inv{x}
\end{aligned}
\end{equation}
This is strictly convex on
\( \mathbb{R}_{++} \), where
\( F”(x) \ge 0 \).
Example:
\begin{equation}\label{eqn:convexOptimizationLecture7:120}
\begin{aligned}
F(x) &= e^{\alpha x} \\
F'(x) &= \alpha e^{\alpha x} \\
F”(x) &= \alpha^2 e^{\alpha x} \ge 0
\end{aligned}
\end{equation}
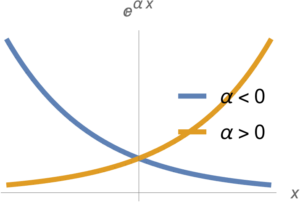
Such functions are plotted in fig. 2, and are convex function for all \( \alpha \).
Example:
For symmetric \( P \in S^n \)
\begin{equation}\label{eqn:convexOptimizationLecture7:140}
\begin{aligned}
F(\Bx) &= \Bx^\T P \Bx + 2 \Bq^\T \Bx + r \\
\spacegrad F &= (P + P^\T) \Bx + 2 \Bq = 2 P \Bx + 2 \Bq \\
\spacegrad^2 F &= 2 P.
\end{aligned}
\end{equation}
This is convex(concave) if \( P \ge 0 \) (\( P \le 0\)).
Example:
A quadratic function
\begin{equation}\label{eqn:convexOptimizationLecture7:780}
F(x, y) = x^2 + y^2 + 3 x y,
\end{equation}
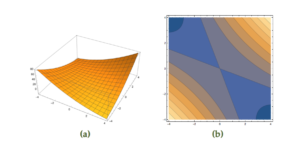
that is neither convex nor concave is plotted in fig 3.
This function can be put in matrix form
\begin{equation}\label{eqn:convexOptimizationLecture7:160}
F(x, y) = x^2 + y^2 + 3 x y
=
\begin{bmatrix}
x & y
\end{bmatrix}
\begin{bmatrix}
1 & 1.5 \\
1.5 & 1
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix},
\end{equation}
and has the Hessian
\begin{equation}\label{eqn:convexOptimizationLecture7:180}
\begin{aligned}
\spacegrad^2 F
&=
\begin{bmatrix}
\partial_{xx} F & \partial_{xy} F \\
\partial_{yx} F & \partial_{yy} F \\
\end{bmatrix} \\
&=
\begin{bmatrix}
2 & 3 \\
3 & 2
\end{bmatrix} \\
&= 2 P.
\end{aligned}
\end{equation}
From the plot we know that this is not PSD, but this can be confirmed by checking the eigenvalues
\begin{equation}\label{eqn:convexOptimizationLecture7:200}
\begin{aligned}
0
&=
\det ( P – \lambda I ) \\
&=
(1 – \lambda)^2 – 1.5^2,
\end{aligned}
\end{equation}
which has solutions
\begin{equation}\label{eqn:convexOptimizationLecture7:220}
\lambda = 1 \pm \frac{3}{2} = \frac{3}{2}, -\frac{1}{2}.
\end{equation}
This is not PSD nor negative semi-definite, because it has one positive and one negative eigenvalues. This is neither convex nor concave.
Along \( y = -x \),
\begin{equation}\label{eqn:convexOptimizationLecture7:240}
\begin{aligned}
F(x,y)
&=
F(x,-x) \\
&=
2 x^2 – 3 x^2 \\
&=
– x^2,
\end{aligned}
\end{equation}
so it is concave along this line. Along \( y = x \)
\begin{equation}\label{eqn:convexOptimizationLecture7:260}
\begin{aligned}
F(x,y)
&=
F(x,x) \\
&=
2 x^2 + 3 x^2 \\
&=
5 x^2,
\end{aligned}
\end{equation}
so it is convex along this line.
Example:
\begin{equation}\label{eqn:convexOptimizationLecture7:280}
F(\Bx) = \sqrt{ x_1 x_2 },
\end{equation}
on \( \textrm{dom} F = \setlr{ x_1 \ge 0, x_2 \ge 0 } \)
For the Hessian
\begin{equation}\label{eqn:convexOptimizationLecture7:300}
\begin{aligned}
\PD{x_1}{F} &= \frac{1}{2} x_1^{-1/2} x_2^{1/2} \\
\PD{x_2}{F} &= \frac{1}{2} x_2^{-1/2} x_1^{1/2}
\end{aligned}
\end{equation}
The Hessian components are
\begin{equation}\label{eqn:convexOptimizationLecture7:320}
\begin{aligned}
\PD{x_1}{} \PD{x_1}{F} &= -\frac{1}{4} x_1^{-3/2} x_2^{1/2} \\
\PD{x_1}{} \PD{x_2}{F} &= \frac{1}{4} x_2^{-1/2} x_1^{-1/2} \\
\PD{x_2}{} \PD{x_1}{F} &= \frac{1}{4} x_1^{-1/2} x_2^{-1/2} \\
\PD{x_2}{} \PD{x_2}{F} &= -\frac{1}{4} x_2^{-3/2} x_1^{1/2}
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:convexOptimizationLecture7:340}
\spacegrad^2 F
=
-\frac{\sqrt{x_1 x_2}}{4}
\begin{bmatrix}
\inv{x_1^2} & -\inv{x_1 x_2} \\
-\inv{x_1 x_2} & \inv{x_2^2}
\end{bmatrix}.
\end{equation}
Checking this for PSD against \( \Bv = (v_1, v_2) \), we have
\begin{equation}\label{eqn:convexOptimizationLecture7:360}
\begin{aligned}
\begin{bmatrix}
v_1 & v_2
\end{bmatrix}
\begin{bmatrix}
\inv{x_1^2} & -\inv{x_1 x_2} \\
-\inv{x_1 x_2} & \inv{x_2^2}
\end{bmatrix}
\begin{bmatrix}
v_1 \\ v_2
\end{bmatrix}
&=
\begin{bmatrix}
v_1 & v_2
\end{bmatrix}
\begin{bmatrix}
\inv{x_1^2} v_1 -\inv{x_1 x_2} v_2 \\
-\inv{x_1 x_2} v_1 + \inv{x_2^2} v_2
\end{bmatrix} \\
&=
\lr{ \inv{x_1^2} v_1 -\inv{x_1 x_2} v_2 } v_1 +
\lr{ -\inv{x_1 x_2} v_1 + \inv{x_2^2} v_2 } v_2
\\
&=
\inv{x_1^2} v_1^2
+ \inv{x_2^2} v_2^2
-2 \inv{x_1 x_2} v_1 v_2 \\
&=
\lr{
\frac{v_1}{x_1}
-\frac{v_2}{x_2}
}^2 \\
&\ge 0,
\end{aligned}
\end{equation}
so \( \spacegrad^2 F \le 0 \). This is a negative semi-definite function (concave). Observe that this check required checking PSD for all values of \( \Bx \).
This is an example of a more general result
\begin{equation}\label{eqn:convexOptimizationLecture7:380}
F(x) = \lr{ \prod_{i = 1}^n x_i }^{1/n},
\end{equation}
which is concave (prove on homework).
Summary.
If \( F \) is differentiable in \R{n}, then check the curvature of the function along all lines. i.e. At all locations and in all directions.
If the Hessian is PSD at all \( \Bx \in \textrm{dom} F \), that is
\begin{equation}\label{eqn:convexOptimizationLecture7:400}
\spacegrad^2 F \ge 0 \, \forall \Bx \in \textrm{dom} F,
\end{equation}
then the function is convex.
more examples of convex, but not necessarily differentiable functions
Example:
Over \( \textrm{dom} F = \mathbb{R}^n \)
\begin{equation}\label{eqn:convexOptimizationLecture7:420}
F(\Bx) = \max_{i = 1}^n x_i
\end{equation}
i.e.
\begin{equation}\label{eqn:convexOptimizationLecture7:440}
\begin{aligned}
F((1,2) &= 2 \\
F((3,-1) &= 3
\end{aligned}
\end{equation}
Example:
\begin{equation}\label{eqn:convexOptimizationLecture7:460}
F(\Bx) = \max_{i = 1}^n F_i(\Bx),
\end{equation}
where
\begin{equation}\label{eqn:convexOptimizationLecture7:480}
F_i(\Bx)
=
… ?
\end{equation}
max of a set of convex functions is a convex function.
Example:
\begin{equation}\label{eqn:convexOptimizationLecture7:500}
F(x) =
x_{[1]} +
x_{[2]} +
x_{[3]}
\end{equation}
where
\( x_{[k]} \) is the k-th largest number in the list
Write
\begin{equation}\label{eqn:convexOptimizationLecture7:520}
F(x) = \max x_i + x_j + x_k
\end{equation}
\begin{equation}\label{eqn:convexOptimizationLecture7:540}
(i,j,k) \in \binom{n}{3}
\end{equation}
Example:
For \( \Ba \in \mathbb{R}^n \) and \( b_i \in \mathbb{R} \)
\begin{equation}\label{eqn:convexOptimizationLecture7:560}
\begin{aligned}
F(\Bx)
&= \sum_{i = 1}^n \log( b_i – \Ba^\T \Bx )^{-1} \\
&= -\sum_{i = 1}^n \log( b_i – \Ba^\T \Bx )
\end{aligned}
\end{equation}
This \( b_i – \Ba^\T \Bx \) is an affine function of \( \Bx \) so it doesn’t affect convexity.
Since \( \log \) is concave, \( -\log \) is convex. Convex functions of affine function of \( \Bx \) is convex function of \( \Bx \).
Example:
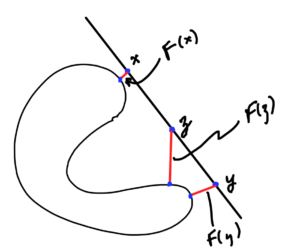
\begin{equation}\label{eqn:convexOptimizationLecture7:580}
F(\Bx) = \sup_{\By \in C} \Norm{ \Bx – \By }
\end{equation}
Here \( C \subseteq \mathbb{R}^n \) is not necessarily convex. We are using \( \sup \) here because the set \( C \) may be open. This function is the length of the line from \( \Bx \) to the point in \( C \) that is furthest from \( \Bx \).
- \( \Bx – \By \) is linear in \( \Bx \)
- \( g_\By(\Bx) = \Norm{\Bx – \By} \) is convex in \( \Bx \) since norms are convex functions.
- \( F(\Bx) = \sup_{\By \in C} \Norm{ \Bx – \By } \). Each \( \By \) index is a convex function. Taking max of those.
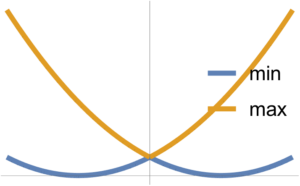
Example:
\begin{equation}\label{eqn:convexOptimizationLecture7:600}
F(\Bx) = \inf_{\By \in C} \Norm{ \Bx – \By }.
\end{equation}
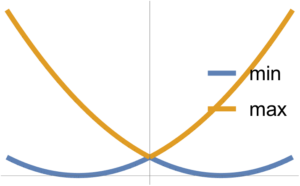
Min and max of two convex functions are plotted in fig. 4.
The max is observed to be convex, whereas the min is not necessarily so.
\begin{equation}\label{eqn:convexOptimizationLecture7:800}
F(\Bz) = F(\theta \Bx + (1-\theta) \By) \ge \theta F(\Bx) + (1-\theta)F(\By).
\end{equation}
This is not necessarily convex for all sets \( C \subseteq \mathbb{R}^n \), because the \( \inf \) of a bunch of convex function is not necessarily convex. However, if \( C \) is convex, then \( F(\Bx) \) is convex.
Consequences of convexity for differentiable functions
- Think about unconstrained functions \( \textrm{dom} F = \mathbb{R}^n \).
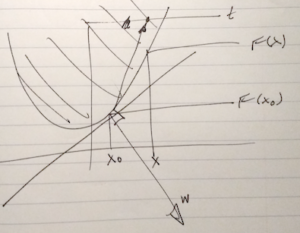
- By first order condition \( F \) is convex iff the domain is convex and
\begin{equation}\label{eqn:convexOptimizationLecture7:620}
F(\Bx) \ge \lr{ \spacegrad F(\Bx)}^\T (\By – \Bx) \, \forall \Bx, \By \in \textrm{dom} F.
\end{equation}
If \( F \) is convex and one can find an \( \Bx^\conj \in \textrm{dom} F \) such that
\begin{equation}\label{eqn:convexOptimizationLecture7:640}
\spacegrad F(\Bx^\conj) = 0,
\end{equation}
then
\begin{equation}\label{eqn:convexOptimizationLecture7:660}
F(\By) \ge F(\Bx^\conj) \, \forall \By \in \textrm{dom} F.
\end{equation}
If you can find the point where the gradient is zero (which can’t always be found), then \( \Bx^\conj\) is a global minimum of \( F \).
Conversely, if \( \Bx^\conj \) is a global minimizer of \( F \), then \( \spacegrad F(\Bx^\conj) = 0 \) must hold. If that were not the case, then you would be able to find a direction to move downhill, contracting the optimality of \( \Bx^\conj\).
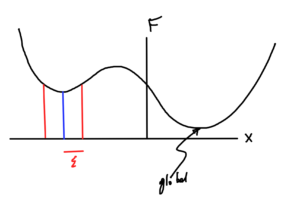
Local vs Global optimum
Definition: Local optimum
\( \Bx^\conj \) is a local optimum of \( F \) if \( \exists \epsilon > 0 \) such that \( \forall \Bx \), \( \Norm{\Bx – \Bx^\conj} < \epsilon \), we have
\begin{equation*}
F(\Bx^\conj) \le F(\Bx)
\end{equation*}
Theorem:
Suppose \( F \) is twice continuously differentiable (not necessarily convex)
- If \( \Bx^\conj\) is a local optimum then\begin{equation*}
\begin{aligned}
\spacegrad F(\Bx^\conj) &= 0 \\
\spacegrad^2 F(\Bx^\conj) \ge 0
\end{aligned}
\end{equation*} - If
\begin{equation*}
\begin{aligned}
\spacegrad F(\Bx^\conj) &= 0 \\
\spacegrad^2 F(\Bx^\conj) \ge 0
\end{aligned},
\end{equation*}then \( \Bx^\conj\) is a local optimum.
Proof:
- Let \( \Bx^\conj \) be a local optimum. Pick any \( \Bv \in \mathbb{R}^n \).\begin{equation}\label{eqn:convexOptimizationLecture7:720}
\lim_{t \rightarrow 0} \frac{ F(\Bx^\conj + t \Bv) – F(\Bx^\conj)}{t}
= \lr{ \spacegrad F(\Bx^\conj) }^\T \Bv
\ge 0.
\end{equation}
Here the fraction is \( \ge 0 \) since \( \Bx^\conj \) is a local optimum.
Since the choice of \( \Bv \) is arbitrary, the only case that you can ensure that \( \ge 0, \forall \Bv \) is
\begin{equation}\label{eqn:convexOptimizationLecture7:740}
\spacegrad F = 0,
\end{equation}
( or else could pick \( \Bv = -\spacegrad F(\Bx^\conj) \).
This means that \( \spacegrad F(\Bx^\conj) = 0 \) if \( \Bx^\conj \) is a local optimum.
Consider the 2nd order derivative
\begin{equation}\label{eqn:convexOptimizationLecture7:760}
\begin{aligned}
\lim_{t \rightarrow 0} \frac{ F(\Bx^\conj + t \Bv) – F(\Bx^\conj)}{t^2}
&=
\lim_{t \rightarrow 0} \inv{t^2}
\lr{
F(\Bx^\conj) + t \lr{ \spacegrad F(\Bx^\conj) }^\T \Bv + \inv{2} t^2 \Bv^\T \spacegrad^2 F(\Bx^\conj) \Bv + O(t^3)
– F(\Bx^\conj)
} \\
&=
\inv{2} \Bv^\T \spacegrad^2 F(\Bx^\conj) \Bv \\
&\ge 0.
\end{aligned}
\end{equation}
Here the \( \ge \) condition also comes from the fraction, based on the optimiality of \( \Bx^\conj \). This is true for all choice of \( \Bv \), thus \( \spacegrad^2 F(\Bx^\conj) \).
References
[1] Stephen Boyd and Lieven Vandenberghe. Convex optimization. Cambridge university press, 2004.