[Click here for a PDF version of this post]
Sinc squared.
This is problem 31(g) from [1]. Find
\begin{equation}\label{eqn:sincSquared:20}
I = \int_{-\infty}^\infty \frac{\sin^2 x}{x^2} dx.
\end{equation}
We will use the same upper half plane semicircular contour, enclosing the second order pole at the origin. This time we write
\begin{equation}\label{eqn:sincSquared:40}
\sin^2 x = \frac{ 1 – \cos\lr{ 2x } }{2},
\end{equation}
allowing us to write
\begin{equation}\label{eqn:sincSquared:60}
\begin{aligned}
I
&= \inv{2} \int_{-\infty}^\infty \frac{1 – \cos\lr{ 2 x } }{x^2} dx \\
&= \inv{2} \textrm{Re} \int_{-\infty}^\infty \frac{1 – e^{2 i x } }{x^2} dx.
\end{aligned}
\end{equation}
This has exactly the structure required to apply Jordan’s lemma, and conclude that the integral over the infinite semicircular part of the contour is zero.
We can proceed to compute the residues
\begin{equation}\label{eqn:sincSquared:80}
\begin{aligned}
I
&=
\inv{2} \textrm{Re} \oint \frac{1 – e^{2 i z } }{z^2} dz \\
&=
\inv{2} \textrm{Re} \frac{ \pi i }{1!} \evalbar{ \lr{1 – e^{2 i z } }’ }{ z = 0 }.
\end{aligned}
\end{equation}
Because we are sneaking around the pole at the origin with a half semicircle, we multiply the residue by \( \pi i \), not \( 2 \pi i \). This leaves
\begin{equation}\label{eqn:sincSquared:100}
I = \textrm{Re} \frac{\pi i}{2} \evalbar{ (- 2 i) e^{2 i z } }{ z = 0 },
\end{equation}
or
\begin{equation}\label{eqn:sincSquared:640}
\boxed{
I = \pi.
}
\end{equation}
An fractional exponent integral.
Next, let’s do 31(h). Given \( 0 < a < 1 \), we want to evaluate \begin{equation}\label{eqn:sincSquared:120} I = \int_0^\infty \frac{x^{2 a – 1}}{x^2 + b^2} dx. \end{equation} Let’s start with a \( x = b u \), where we assume that \( b > 0 \). This gives us
\begin{equation}\label{eqn:sincSquared:140}
\begin{aligned}
I
&= \int_0^\infty \frac{ b^{2 a – 1} u^{2 a – 1}}{b^2 \lr{ u^2 + 1 } } b du \\
&= b^{2(a – 1)} \int_0^\infty \frac{ u^{2 a – 1}}{u^2 + 1 } du.
\end{aligned}
\end{equation}
We now want to solve the slightly simpler integral, let’s call it
\begin{equation}\label{eqn:sincSquared:160}
J = \int_0^\infty \frac{ u^{2 a – 1}}{u^2 + 1 } du.
\end{equation}
Let’s now look at
\begin{equation}\label{eqn:sincSquared:180}
\begin{aligned}
K
&= \int_{-\infty}^0 \frac{ u^{2 a – 1}}{u^2 + 1 } du \\
&= -\int_{\infty}^0 \frac{ \lr{ – v } ^{2 a – 1}}{v^2 + 1 } dv \\
&= \lr{-1}^{2 a – 1} J.
\end{aligned}
\end{equation}
However
\begin{equation}\label{eqn:sincSquared:200}
\begin{aligned}
\lr{-1}^{2 a – 1}
&=
e^{i \pi \lr{ 2 a – 1 } } \\
&=
– e^{2 i \pi a },
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:sincSquared:220}
\begin{aligned}
J
&= \inv{ 1 – e^{2 i \pi a } } \int_{-\infty, \infty} \frac{ u^{2 a – 1}}{u^2 + 1 } du \\
&= \inv{ 1 – e^{2 i \pi a } } \oint \frac{ z^{2 a – 1}}{z^2 + 1 } dz,
\end{aligned}
\end{equation}
that is, assuming the integral on the upper half plane semicircle is zero.
On that semicircle, with \( z = R e^{i\theta} \),
\begin{equation}\label{eqn:sincSquared:240}
\begin{aligned}
\oint \frac{ z^{2 a – 1}}{z^2 + 1 } dz
&= \int_0^\pi \frac{ \lr{ R e^{i \theta} }^{2 a – 1} }{ R^2 e^{2 i \theta} + 1 } R e^{i \theta} d\theta \\
&\rightarrow \int_0^\pi R^{2 a – 1 + 1 – 2} e^{i \theta (2 a – 1) -i \theta} d\theta.
\end{aligned}
\end{equation}
Near \( a \approx 0 \) this is \( O(R^{-2}) \), which tends to zero. At the upper tend of the a range, where \( a = 1 – \epsilon \), this is
\begin{equation}\label{eqn:sincSquared:260}
O(R^{2(1 – \epsilon) – 2}) = O(1/R^{2 \epsilon}),
\end{equation}
which also tends to zero. We have only one enclosed pole, at \( z = i \), so
\begin{equation}\label{eqn:sincSquared:280}
\begin{aligned}
I
&= \frac{b^{2(a-1)}}{ 1 – e^{2 i \pi a } } ( 2 \pi i ) \evalbar{ \frac{z^{2 a – 1}}{z + i} }{z = i} \\
&= \frac{\pi b^{2(a-1)}}{ 1 – e^{2 i \pi a } } i^{2 a – 1}.
\end{aligned}
\end{equation}
But
\begin{equation}\label{eqn:sincSquared:300}
\begin{aligned}
i^{2 a – 1}
&= \lr{ e^{i \pi/2} }^{2 a – 1} \\
&= e^{i \pi a} e^{-i \pi/2} \\
&= -i e^{i \pi a},
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:sincSquared:320}
\begin{aligned}
I
&= \frac{-i \pi b^{2(a-1)} e^{i \pi a}}{ 1 – e^{2 i \pi a } } \\
&= \frac{-i \pi b^{2(a-1)} }{ e^{-i \pi a} – e^{i \pi a } },
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:sincSquared:660}
\boxed{
I = \frac{\pi b^{2(a-1)} }{ 2 \sin\lr{ \pi a } }.
}
\end{equation}
A log integral over the positive x-axis.
Problem 31(i) is
\begin{equation}\label{eqn:sincSquared:340}
I = \int_0^\infty \frac{\ln x}{x^2 + b^2} dx.
\end{equation}
Let’s see what happens to this integral over the \( x < 0 \) range.
\begin{equation}\label{eqn:sincSquared:360}
\begin{aligned}
\int_{-\infty}^0 \frac{\ln x}{x^2 + b^2} dx
&=
-\int_{\infty}^0 \frac{\ln(- u)}{u^2 + b^2} d u \\
&=
I + \int_0^\infty \frac{\ln e^{i \pi}}{u^2 + b^2} du \\
&=
I + \frac{i \pi}{2} \int_{-\infty}^\infty \inv{u^2 + b^2} du.
\end{aligned}
\end{equation}
This means that we have
\begin{equation}\label{eqn:sincSquared:380}
\int_{-\infty}^\infty \frac{\ln x}{x^2 + b^2} dx = 2 I + \frac{i \pi}{2} \int_{-\infty}^\infty \inv{u^2 + b^2} du,
\end{equation}
or
\begin{equation}\label{eqn:sincSquared:480}
\begin{aligned}
I
&= \inv{2} \int_{-\infty}^\infty \frac{\ln x – i \pi/2}{x^2 + b^2} dx \\
&= \inv{2} \int_{-\infty}^\infty \frac{\ln(-i x)}{x^2 + b^2} dx \\
&= \inv{2} \oint \frac{\ln(-i z)}{z^2 + b^2} dz \\
&= (\pi i) \evalbar{ \frac{\ln(-i z)}{z + i b} }{z = i b},
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:sincSquared:680}
\boxed{
I = \frac{\pi \ln b}{2 b}.
}
\end{equation}
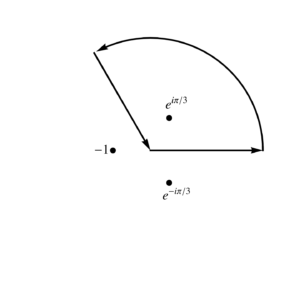
A pie contour.
Skipping ahead to 31(k), we want to find
\begin{equation}\label{eqn:sincSquared:500}
I = \int_0^\infty \frac{dx}{x^3 + a^3}.
\end{equation}
Some googling shows that we can evaluate integrals with \( x^n + b^n \) denominators, using a pie shaped contour, with slice sizes of \( 2 \pi /n \),
as plotted in fig. 1.
Integrating (backwards) along the \( 2 \pi/3 \) slice line, with \( \alpha = e^{\pi i/3} \), and \( z = \alpha^2 u \), we have
\begin{equation}\label{eqn:sincSquared:520}
\begin{aligned}
\int_0^\infty \frac{ \alpha^2 du }{ \alpha^6 u^3 + a^3 }
&=
\alpha^2 \int_0^\infty \frac{ du }{ u^3 + a^3 } \\
&= \alpha^2 I,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:sincSquared:540}
I = \inv{ 1 – \alpha^2 } \oint \frac{dz}{z^3 + a^3}.
\end{equation}
We can factor the denominator as
\begin{equation}\label{eqn:sincSquared:560}
z^3 + a^3 = \lr{ z – \alpha a }\lr{ z + a }\lr{ z – a/\alpha },
\end{equation}
where only the \( z = \alpha a \) pole is enclosed. The residue calculation is
\begin{equation}\label{eqn:sincSquared:580}
\begin{aligned}
I
&= \frac{ 2 \pi i }{1 – \alpha^2 } \evalbar{ \inv{\lr{z + a}\lr{ z – a/\alpha } } }{z = a\alpha} \\
&= \frac{ 2 \pi i }{a^2} \inv{ \lr{1 – \alpha^2 } \lr{ \alpha + 1 } \lr{ \alpha – 1/\alpha } } \\
\end{aligned}
\end{equation}
We now want to expand the denominator. I had trouble simplifying this by hand, and it took me a few tries to get it right:
\begin{equation}\label{eqn:sincSquared:600}
\begin{aligned}
-\lr{1 – \alpha^2 } \lr{ \alpha + 1 } \lr{ \alpha – 1/\alpha }
&=
-\frac{\lr{\alpha^2 -1}^2 \lr{ \alpha + 1 }}{\alpha} \\
&=
-\lr{ e^{2 \pi i/3} – 1}^2 \lr{ 1 + e^{i\pi/3} } e^{-i\pi/3} \\
&=
-\lr{ e^{4 \pi i/3} + 1 – 2 e^{ 2 \pi i /3} } \lr{ 1 + e^{-i\pi/3} } \\
&=
-\lr{ e^{4 \pi i/3} + 1 – 2 e^{ 2 \pi i /3} + e^{3 \pi i/3} + e^{-i\pi/3} – 2 e^{ \pi i /3} } \\
&=
-\lr{ e^{4 \pi i/3} – 2 e^{ 2 \pi i /3} + e^{-i\pi/3} – 2 e^{ \pi i /3} } \\
&=
-\lr{ \inv{2} \lr{ -1 – \sqrt{3} i } – \lr{-1 + \sqrt{3} i} + \inv{2}\lr{ 1 – \sqrt{3} i } – \lr{ 1 + \sqrt{3} i} } \\
&=
-\lr{ -\inv{2} – 1 – \inv{2} – 1 } \sqrt{3} i \\
&=
3 \sqrt{3} i.
\end{aligned}
\end{equation}
Putting the pieces together
\begin{equation}\label{eqn:sincSquared:620}
\boxed{
I = \frac{2 \pi}{3 \sqrt{3} a^2}.
}
\end{equation}
References
[1] F.W. Byron and R.W. Fuller. Mathematics of Classical and Quantum Physics. Dover Publications, 1992.