Marks are in for Winter 2016

May 18, 2016 Incoherent ramblings ece1229, ece1254, phy1520, phy1610, phy356, phy450, phy452, phy454, phy456, phy485, phy487, University of Toronto

I started my formal re-education program back in 2010 after 20 years out of school. The first few courses were particularly tough after such a long break from school (and exam based courses still are), but I’m getting the hang of playing that game again. Here’s my score so far:

Crs Code  Title                                    Wgt  Mrk  Grd    CrsAvg
PHY356H1  Quantum Mechanics I                      0.50  78  B+     C+
PHY450H1  Rel Electrodynamics                      0.50  78  B+     *
PHY456H1  Quantum Mechanics II                     0.50  72  B-     C+
PHY454H1  Continuum Mech                           0.50  85  A      B
PHY485H1  Adv Classical Optics                     0.50  85  A      *
PHY452H1  Basic Stat Mechanics                     0.50  81  A-     B-
PHY487H1  Condensed Matter I                       0.50  80  A-     B+
ECE1254H  Modeling of Multiphysics Systems         0.50      A+
ECE1229H  Advanced Antenna Theory                  0.50      A-
PHY1520H  Quantum Mechanics                        0.50      A-
PHY1610H  Scientific Computing for Physicists      0.50      A+

This last grad course is the only one of which they gave (informally through email) a non-letter grade (97). That one happened to be very well suited to me, and did not have anything based on exams nor on presentations (just assignments). They were demanding assignments (and fun), so I had to work really hard for that 97.

As a returning student I really suck at classes that have marks that are highly biased towards exams. My days of showing up late for class, sleeping through big chunks of the parts that I did get their in time for, and still breezing through the exams are long gone. Somehow in my youth I could do that, and still be able to quickly and easily barf out all the correct exam answers without thinking about it. I got a 99 in first year calculus doing exactly that, although it helped that the Central Technical School’s math department kicked butt, and left Prof Smith with only a review role.

Now I take a lot more time thinking things through, and also take a lot of time writing up my notes (which would sometimes have been spent better doing practise problems). It’s funny thinking back to undergrad where I had such scorn for anybody that took notes. Now I do just that, but in latex. I would be the object of my own scorn X10, if I met my teenage self again!

A matrix formulation of the Harmonic Balance method non-linear currents

December 14, 2014 ece1254 ece1254, Harmonic Balance, Jacobian, multivariable Newton's method, Newton's method, non-linear circuit, non-linear equation

[Click here for a PDF of this post with nicer formatting]

Because it was simple, a coordinate expansion of the Jacobian of the non-linear currents was good to get a feeling for the structure of the equations. However, a Jacobian of that form is impossibly slow to compute for larger \( N \). It seems plausible that eliminating the coordinate expansion, expressing both the currrent and the Jacobian directly in terms of the Harmonic Balance unknowns vector \( \BV \), would lead to a simpler set of equations that could be implemented in a computationally more effective way. To aid in this discovery, consider the simple RC load diode circuit of fig. 1. It’s not too hard to start from scratch with the time domain nodal equations for this circuit, which are

fig. 1. Simple diode and resistor circuit

\( 0 = i_s – i_d \)
\( Z v^{(2)} + C dv^{(2)}/dt = i_d \)
\( i_d = I_0 \lr{ e^{(v^{(1)} – v^{(2)})/V_T} – 1} \)

To setup for matrix form, let

\begin{equation}\label{eqn:diodeRLCSample:1240}
\Bv(t) =
\begin{bmatrix}
v^{(1)}(t) \\
v^{(2)}(t) \\
\end{bmatrix}
\end{equation}
\begin{equation}\label{eqn:diodeRLCSample:1140}
\BG =
\begin{bmatrix}
0 & 0 \\
0 & Z \\
\end{bmatrix}
\end{equation}
\begin{equation}\label{eqn:diodeRLCSample:1160}
\BC =
\begin{bmatrix}
0 & 0 \\
0 & C \\
\end{bmatrix}
\end{equation}
\begin{equation}\label{eqn:diodeRLCSample:1180}
\Bd =
\begin{bmatrix}
1 \\
-1
\end{bmatrix}
\end{equation}
\begin{equation}\label{eqn:diodeRLCSample:1200}
\Bb =
\begin{bmatrix}
1 \\
0
\end{bmatrix},
\end{equation}

so that the time domain equations can be written as

\begin{equation}\label{eqn:diodeRLCSample:1220}
\BG \Bv(t)
+ \BC \Bv'(t)
=
\Bb i_s(t)
+
I_0
\Bd
\lr{
e^{ (v^{(1)}(t) – v^{(2)}(t))/V_T} – 1
}
=
\begin{bmatrix}
\Bb & -I_0 \Bd
\end{bmatrix}
\begin{bmatrix}
i_s(t) \\
1
\end{bmatrix}
+
I_0 \Bd
e^{ (v^{(1)}(t) – v^{(2)}(t))/V_T}.
\end{equation}

Harmonic Balance is essentially the assumption that the input and outputs are assumed to be a bandwidth limited periodic signal, and the non-linear components can be approximated by the same

\begin{equation}\label{eqn:diodeRLCSample:1260}
i_s(t) = \sum_{n=-N}^N I^{(s)}_n e^{ j \omega_0 n t },
\end{equation}
\begin{equation}\label{eqn:diodeRLCSample:1280}
v^{(k)}(t) =
\sum_{n=-N}^N V^{(k)}_n e^{ j \omega_0 n t },
\end{equation}
\begin{equation}\label{eqn:diodeRLCSample:1300}
\epsilon(t) =
e^{ (v^{(1)}(t) – v^{(2)}(t))/V_T}
\simeq
\sum_{n=-N}^N E_n e^{ j \omega_0 n t },
\end{equation}

The approximation in \ref{eqn:diodeRLCSample:1300} is an equality only at the Nykvist sampling times \( t_k = T k/(2 N + 1) \). The Fourier series provides a periodic extension to other times that will approximate the underlying periodic non-linear relation.

With all the time dependence locked into the exponentials, the derivatives are really easy to calculate

\begin{equation}\label{eqn:diodeRLCSample:1281}
\frac{d}{dt} v^{(k)}(t) =
\sum_{n=-N}^N j \omega_0 n V^{(k)}_n e^{ j \omega_0 n t }.
\end{equation}

Inserting all of these into \ref{eqn:diodeRLCSample:1220} gives

\begin{equation}\label{eqn:diodeRLCSample:1320}
\sum_{n=-N}^N e^{ j \omega_0 n t} \lr{ \BG + j \omega_0 n \BC }
\begin{bmatrix}
V^{(1)}_n \\
V^{(2)}_n \\
\end{bmatrix}
=
\sum_{n=-N}^N e^{ j \omega_0 n t}
\lr{
-I_0 \Bd \delta_{n 0}
+
\Bb I^{(s)}_n
+ I_0 \Bd E_n
}.
\end{equation}

The periodic assumption requires equality for each \( e^{j \omega_0 n t} \), or

\begin{equation}\label{eqn:diodeRLCSample:1340}
\lr{ \BG + j \omega_0 n \BC }
\begin{bmatrix}
V^{(1)}_n \\
V^{(2)}_n \\
\end{bmatrix}
=
-I_0 \Bd \delta_{n 0}
+
\Bb I^{(s)}_n
+ I_0 \Bd E_n.
\end{equation}

For illustration, consider the \( N = 1 \) case, where the block matrix form is

\begin{equation}\label{eqn:diodeRLCSample:1360}
\begin{bmatrix}
\BG + j \omega_0 (-1) \BC & 0 & 0 \\
0 & \BG + j \omega_0 (0) \BC & 0 \\
0 & 0 & \BG + j \omega_0 (1) \BC
\end{bmatrix}
\begin{bmatrix}
\begin{bmatrix}
V^{(1)}_{-1} \\
V^{(2)}_{-1} \\
\end{bmatrix} \\
\begin{bmatrix}
V^{(1)}_{0} \\
V^{(2)}_{0} \\
\end{bmatrix} \\
\begin{bmatrix}
V^{(1)}_{1} \\
V^{(2)}_{1} \\
\end{bmatrix}
\end{bmatrix}
=
\begin{bmatrix}
\Bb I^{(s)}_{-1} \\
\Bb I^{(s)}_{0} – I_0 \Bd \\
\Bb I^{(s)}_{1} \\
\end{bmatrix}
+
I_0
\begin{bmatrix}
\Bd E_{-1} \\
\Bd E_{0} \\
\Bd E_{1} \\
\end{bmatrix}.
\end{equation}

The structure of this equation is

\begin{equation}\label{eqn:diodeRLCSample:1380}
\BY \BV = \BI + \mathcal{I}(\BV),
\end{equation}

The non-linear current \( \mathcal{I}(\BV) \) needs to be examined further. How much of this can be precomputed, and what is the simplest way to compute the Jacobian? With

\begin{equation}\label{eqn:diodeRLCSample:1400}
\BE =
\begin{bmatrix}
E_{-1} \\
E_{0} \\
E_{1} \\
\end{bmatrix}, \qquad
\Bepsilon =
\begin{bmatrix}
\epsilon_{-1} \\
\epsilon_{0} \\
\epsilon_{1} \\
\end{bmatrix},
\end{equation}

the non-linear current is

\begin{equation}\label{eqn:diodeRLCSample:1420}
\mathcal{I} =
I_0
\begin{bmatrix}
\Bd E_{-1} \\
\Bd E_{0} \\
\Bd E_{1} \\
\end{bmatrix}
=
I_0
\begin{bmatrix}
\Bd \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \BE \\
\Bd \begin{bmatrix} 0 & 1 & 0 \end{bmatrix} \BE \\
\Bd \begin{bmatrix} 0 & 0 & 1 \end{bmatrix} \BE
\end{bmatrix}
=
I_0
\begin{bmatrix}
\Bd & 0 & 0 \\
0 & \Bd & 0 \\
0 & 0 & \Bd
\end{bmatrix}
\BF^{-1} \Bepsilon
\end{equation}

In the last step \( \BE = \BF^{-1} \Bepsilon \) has been factored out (in its inverse Fourier form). With

\begin{equation}\label{eqn:diodeRLCSample:1480}
\BD =
\begin{bmatrix}
\Bd & 0 & 0 \\
0 & \Bd & 0 \\
0 & 0 & \Bd \\
\end{bmatrix},
\end{equation}

the current is

\begin{equation}\label{eqn:diodeRLCSample:1540}
\boxed{
\mathcal{I}(\BV) =
I_0 \BD \BF^{-1} \Bepsilon(\BV).
}
\end{equation}

The next step is finding an appropriate form for \( \Bepsilon \)

\begin{equation}\label{eqn:diodeRLCSample:1440}
\begin{aligned}
\Bepsilon &=
\begin{bmatrix}
\epsilon(t_{-1}) \\
\epsilon(t_{0}) \\
\epsilon(t_{1}) \\
\end{bmatrix} \\
&=
\begin{bmatrix}
\exp\lr{ \lr{ v^{(1)}_{-1} – v^{(2)}_{-1} }/V_T } \\
\exp\lr{ \lr{ v^{(1)}_{0} – v^{(2)}_{0} }/V_T } \\
\exp\lr{ \lr{ v^{(1)}_{1} – v^{(2)}_{1} }/V_T }
\end{bmatrix} \\
&=
\begin{bmatrix}
\exp\lr{
\begin{bmatrix}
1 & 0 & 0
\end{bmatrix}
\lr{ \Bv^{(1)} – \Bv^{(2)} }/V_T } \\
\exp\lr{
\begin{bmatrix}
0 & 1 & 0
\end{bmatrix}
\lr{ \Bv^{(1)} – \Bv^{(2)} }/V_T } \\
\exp\lr{
\begin{bmatrix}
0 & 0 & 1
\end{bmatrix}
\lr{ \Bv^{(1)} – \Bv^{(2)} }/V_T } \\
\end{bmatrix} \\
&=
\begin{bmatrix}
\exp\lr{
\begin{bmatrix}
1 & 0 & 0
\end{bmatrix}
\BF
\lr{ \BV^{(1)} – \BV^{(2)} }/V_T } \\
\exp\lr{
\begin{bmatrix}
0 & 1 & 0
\end{bmatrix}
\BF
\lr{ \BV^{(1)} – \BV^{(2)} }/V_T } \\
\exp\lr{
\begin{bmatrix}
0 & 0 & 1
\end{bmatrix}
\BF
\lr{ \BV^{(1)} – \BV^{(2)} }/V_T } \\
\end{bmatrix}.
\end{aligned}
\end{equation}

It would be nice to have the difference of frequency domain vectors expressed in terms of \( \BV \), which can be done with a bit of rearrangement

\begin{equation}\label{eqn:diodeRLCSample:1460}
\begin{aligned}
\BV^{(1)} – \BV^{(2)}
&=
\begin{bmatrix}
V^{(1)}_{-1} – V^{(2)}_{-1} \\
V^{(1)}_{0} – V^{(2)}_{0} \\
V^{(1)}_{1} – V^{(2)}_{1} \\
\end{bmatrix} \\
&=
\begin{bmatrix}
1 & -1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & -1 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & -1 \\
\end{bmatrix}
\begin{bmatrix}
V_{-1}^{(1)} \\
V_{-1}^{(2)} \\
V_{0}^{(1)} \\
V_{0}^{(2)} \\
V_{1}^{(1)} \\
V_{1}^{(2)} \\
\end{bmatrix} \\
&=
\begin{bmatrix}
\Bd^\T & 0 & 0 \\
0 & \Bd^\T & 0 \\
0 & 0 & \Bd^\T \\
\end{bmatrix}
\BV \\
&= \BD^\T \BV,
\end{aligned}
\end{equation}

\begin{equation}\label{eqn:diodeRLCSample:1520}
\BH
=
\BF \BD^\T /V_T
=
\begin{bmatrix}
\Bh_1^\T \\
\Bh_2^\T \\
\Bh_3^\T
\end{bmatrix},
\end{equation}

which allows the non-linear current to can now be completely expressed in terms of \( \BV \).

\begin{equation}\label{eqn:diodeRLCSample:1560}
\boxed{
\Bepsilon(\BV)
=
\begin{bmatrix}
e^{\Bh_1^\T \BV} \\
e^{\Bh_2^\T \BV} \\
e^{\Bh_3^\T \BV} \\
\end{bmatrix}.
}
\end{equation}

Jacobian

With a compact matrix representation of the non-linear current, attention can now be turned to the Jacobian of the non-linear current. Let \( \BA = I_0 \BD \BF^{-1} = [ a_{ij} ]_{ij} \), the current (with summation implied) is

\begin{equation}\label{eqn:diodeRLCSample:1580}
\mathcal{I} =
\begin{bmatrix}
a_{ik} \epsilon_k,
\end{bmatrix}
\end{equation}

with coordinates

\begin{equation}\label{eqn:diodeRLCSample:1600}
\mathcal{I}_i = a_{ik} \epsilon_k = a_{ik} \exp\lr{ \Bh_k^\T \BV }.
\end{equation}

so the Jacobian components are

\begin{equation}\label{eqn:diodeRLCSample:1620}
[\BJ^{\mathcal{I}}]_{ij}
=
a_{ik} \epsilon_k = a_{ik}
\PD{V_j}{}
\exp\lr{ \Bh_k^\T \BV }
=
a_{ik}
h_{kj}
\exp\lr{ \Bh_k^\T \BV }.
\end{equation}

Factoring out \( \BU = [h_{ij} \exp\lr{ \Bh_i^\T \BV }]_{ij} \),

\begin{equation}\label{eqn:diodeRLCSample:1640}
\BJ^{\mathcal{I}}
= \BA \BU
=
\BA
\begin{bmatrix}
\begin{bmatrix} h_{11} & h_{12} & \cdots h_{1, R(2 N + 1)}\end{bmatrix} \exp\lr{ \Bh_1^\T \BV } \\
\begin{bmatrix} h_{21} & h_{22} & \cdots h_{2, R(2 N + 1)}\end{bmatrix} \exp\lr{ \Bh_2^\T \BV } \\
\begin{bmatrix} h_{31} & h_{32} & \cdots h_{3, R(2 N + 1)}\end{bmatrix} \exp\lr{ \Bh_3^\T \BV } \\
\end{bmatrix}
=
\BA
\begin{bmatrix}
\Bh_1^\T \exp\lr{ \Bh_1^\T \BV } \\
\Bh_2^\T \exp\lr{ \Bh_2^\T \BV } \\
\Bh_3^\T \exp\lr{ \Bh_3^\T \BV } \\
\end{bmatrix}.
\end{equation}

A quick sanity check of dimensions seems worthwhile, and shows that all is well

\( \BA \) : \( R(2 N + 1) \times 2 N + 1 \)
\( \BU \) : \( 2 N + 1 \times R(2 N + 1) \)
\( \BJ^{\mathcal{I}} \) : \( R(2 N + 1) \times R(2 N + 1) \)

The Jacobian of the non-linear current is now completely determined

\begin{equation}\label{eqn:diodeRLCSample:1660}
\boxed{
\BJ^{\mathcal{I}}( \BV ) =
I_0 \BD \BF^{-1}
\begin{bmatrix}
\Bh_1^\T \exp\lr{ \Bh_1^\T \BV } \\
\Bh_2^\T \exp\lr{ \Bh_2^\T \BV } \\
\Bh_3^\T \exp\lr{ \Bh_3^\T \BV } \\
\end{bmatrix}.
}
\end{equation}

Newton’s method solution

All the pieces required for a Newton’s method solution are now in place. The goal is to find a value of \( \BV \) that provides the zero

\begin{equation}\label{eqn:diodeRLCSample:1680}
f(\BV) = \BY \BV – \BI – \mathcal{I}(\BV).
\end{equation}

Expansion to first order around an initial guess \( \BV^0 \), gives

\begin{equation}\label{eqn:diodeRLCSample:1700}
f( \BV^0 + \Delta \BV ) = f(\BV^0) + \BJ(\BV^0) \Delta \BV \approx 0,
\end{equation}

where the full Jacobian of \( f(\BV) \) is

\begin{equation}\label{eqn:diodeRLCSample:1720}
\BJ(\BV) = \BY – \BJ^{\mathcal{I}}(\BV).
\end{equation}

The Newton’s method refinement of the initial guess follows by inversion

\begin{equation}\label{eqn:diodeRLCSample:1740}
\Delta \BV = -\lr{ \BY – \BJ^{\mathcal{I}}(\BV^0) }^{-1} f(\BV^0).
\end{equation}

Development of Harmonic balance equations (considering a sample diode RLC circuit)

December 9, 2014 ece1254 discrete time sample, ece1254, Fourier series, frequency domain, Harmonic Balance, phasor, time domain

[Click here for a PDF of this post with nicer formatting]

Previously, the time domain MNA equations and first steps at producing the Harmonic Balance equations were performed. That was a frequency domain analysis with an assumed Fourier solution associated with discrete time sampling.

The next goal is to put this in block matrix form. First introducing discrete time sampling vectors

\begin{equation}\label{eqn:diodeRLCSample:100}
\Bv_a =
\begin{bmatrix}
v_a(t_{-N}) \\
v_a(t_{1-N}) \\
\vdots \\
v_a(t_{N-1}) \\
v_a(t_{N}) \\
\end{bmatrix}, \qquad
\Bu_a =
\begin{bmatrix}
u_b(t_{-N}) \\
u_b(t_{1-N}) \\
\vdots \\
u_b(t_{N-1}) \\
u_b(t_{N}) \\
\end{bmatrix}, \qquad
\Bw_a =
\begin{bmatrix}
w_c(t_{-N}) \\
w_c(t_{1-N}) \\
\vdots \\
w_c(t_{N-1}) \\
w_c(t_{N}) \\
\end{bmatrix},
\end{equation}

and Fourier component vectors

\begin{equation}\label{eqn:diodeRLCSample:120}
\BV_a =
\begin{bmatrix}
V^{(a)}_{-N} \\
V^{(a)}_{1-N} \\
\vdots \\
V^{(a)}_{N-1} \\
V^{(a)}_{N} \\
\end{bmatrix}, \qquad
\BU_b =
\begin{bmatrix}
U^{(b)}_{-N} \\
U^{(b)}_{1-N} \\
\vdots \\
U^{(b)}_{N-1} \\
U^{(b)}_{N} \\
\end{bmatrix}, \qquad
\BW_c =
\begin{bmatrix}
W^{(c)}_{-N} \\
W^{(c)}_{1-N} \\
\vdots \\
W^{(c)}_{N-1} \\
W^{(c)}_{N} \\
\end{bmatrix}.
\end{equation}

With \( \alpha = e^{ 2 \pi j /(2 N + 1) } \), and

\begin{equation}\label{eqn:diodeRLCSample:140}
\BF =
\begin{bmatrix}
\alpha^{ N N } & \alpha^{ \lr{N-1} N } & \cdots & 1 & \cdots & \alpha^{ -\lr{N-1} N } & \alpha^{ -N N } \\
\alpha^{ N \lr{N-1} } & \alpha^{ \lr{N-1} \lr{N-1} } & \cdots & 1 & \cdots & \alpha^{ -\lr{N-1} \lr{N-1} } & \alpha^{ -N \lr{N-1} } \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
1 & 1 & 1 & 1 & 1 & 1 & 1 \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
\alpha^{ -N \lr{N-1} } & \alpha^{ -\lr{N-1} \lr{N-1} } & \cdots & 1 & \cdots & \alpha^{ {N-1} \lr{N-1} } & \alpha^{ N \lr{N-1} } \\
\alpha^{ -N N } & \alpha^{ -N N } & \cdots & 1 & \cdots & \alpha^{ \lr{N-1} N } & \alpha^{ N N } \\
\end{bmatrix},
\end{equation}

in each case the time domain sampling vectors are related to the Fourier components by relations of the form

\begin{equation}\label{eqn:diodeRLCSample:160}
\Bx = \BF \BX.
\end{equation}

Block matrix form, with physical parameter ordering

To understand how to put \ref{eqn:diodeRLCSample:240} in block matrix form, it is helpful to consider a specific example. Consider again the specific example of the RLC circuit above, which has the form

\begin{equation}\label{eqn:diodeRLCSample:260}
\begin{bmatrix}
0 & 0 & 0 & 0 \\
0 & Z & -Z & 1 \\
0 & -Z & Z + j \omega_0 n C & 0 \\
0 & -1 & 0 & + j \omega_0 n L \\
\end{bmatrix}
\begin{bmatrix}
V_n^{(1)} \\
V_n^{(2)} \\
V_n^{(3)} \\
I_n^{(L)} \\
\end{bmatrix}
=
\begin{bmatrix}
I_n^{(1)} \\
I_n^{(2)} \\
I_n^{(3)} \\
I_n^{(4)} \\
\end{bmatrix}
\end{equation}

Here the \( I^{(i)} \) terms are the DFT representations of both the linear and non-linear sources.

Suppose for example that \( N = 1 \). One way to write \ref{eqn:diodeRLCSample:260} would be

\begin{equation}\label{eqn:diodeRLCSample:320}
\begin{aligned}
&
\begin{bmatrix}
I_{-1}^{(1)} \\
I_0^{(1)} \\
I_{1}^{(1)} \\
I_{-1}^{(2)} \\
I_0^{(2)} \\
I_{1}^{(2)} \\
I_{-1}^{(3)} \\
I_0^{(3)} \\
I_{1}^{(3)} \\
I_{-1}^{(4)} \\
I_0^{(4)} \\
I_{1}^{(4)} \\
\end{bmatrix}
=
\left[
\begin{array}{c|c|c|c}
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} \\ \hline
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
Z & 0 & 0 \\
0 & Z & 0 \\
0 & 0 & Z \\
\end{matrix} &
\begin{matrix}
-Z & 0 & 0 \\
0 & -Z & 0 \\
0 & 0 & -Z \\
\end{matrix} &
\begin{matrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{matrix} \\ \hline
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
-Z & 0 & 0 \\
0 & -Z & 0 \\
0 & 0 & -Z \\
\end{matrix} &
\begin{matrix}
Z & 0 & 0 \\
0 & Z & 0 \\
0 & 0 & Z \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} \\ \hline
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
-1 & 0 & 0 \\
0 & -1 & 0 \\
0 & 0 & -1 \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} \\
\end{array}
\right]
\begin{bmatrix}
V_{-1}^{(1)} \\
V_{0}^{(1)} \\
V_{1}^{(1)} \\
V_{-1}^{(2)} \\
V_{0}^{(2)} \\
V_{1}^{(2)} \\
V_{-1}^{(3)} \\
V_{0}^{(3)} \\
V_{1}^{(3)} \\
I_{-1}^{(L)} \\
I_{0}^{(L)} \\
I_{1}^{(L)} \\
\end{bmatrix} \\
&+
\left[
\begin{array}{c|c|c|c}
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} \\ \hline
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} \\ \hline
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
j \omega_0 (-1) C & 0 & 0 \\
0 & j \omega_0 (0) C & 0 \\
0 & 0 & j \omega_0 (1) C \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} \\ \hline
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} &
\begin{matrix}
j \omega_0 (-1) L & 0 & 0 \\
0 & j \omega_0 (0) L & 0 \\
0 & 0 & j \omega_0 (1) L \\
\end{matrix} \\
\end{array}
\right]
\begin{bmatrix}
V_{-1}^{(1)} \\
V_{0}^{(1)} \\
V_{1}^{(1)} \\
V_{-1}^{(2)} \\
V_{0}^{(2)} \\
V_{1}^{(2)} \\
V_{-1}^{(3)} \\
V_{0}^{(3)} \\
V_{1}^{(3)} \\
I_{-1}^{(L)} \\
I_{0}^{(L)} \\
I_{1}^{(L)} \\
\end{bmatrix} \\
\end{aligned}
\end{equation}

With a vector of fourier coeffient vectors

\begin{equation}\label{eqn:diodeRLCSample:280}
\BV =
\begin{bmatrix}
\BV^{(1)} \\
\BV^{(2)} \\
\BV^{(3)} \\
\BI^{(L)}
\end{bmatrix}, \qquad
\BI =
\begin{bmatrix}
\BI^{(1)} \\
\BI^{(2)} \\
\BI^{(3)} \\
\BI^{(4)}
\end{bmatrix}.
\end{equation}

and a \( (2 N + 1) \times (2 N + 1) \) matrix of indexes

\begin{equation}\label{eqn:diodeRLCSample:220}
\BN =
\begin{bmatrix}
-N & & & & \\
& 1-N & & & \\
& & \ddots & & \\
& & & N-1 & \\
& & & & N \\
\end{bmatrix},
\end{equation}

the complete block diagonalization is

\begin{equation}\label{eqn:diodeRLCSample:300}
\boxed{
{\begin{bmatrix}
g_{rs} \BI_{2 N + 1} +
j \omega_0 c_{rs} \BN
\end{bmatrix}
}_{rs}
\BV
=
\BI.
}
\end{equation}

Block matrix form, with frequency ordering

It turns out that a better way of ordering the vector of Fourier components is using a frequency ordering that interleaves the physical parameters. With such an ordering the DFT MNA equations are

\begin{equation}\label{eqn:diodeRLCSample:340}
\begin{aligned}
\BI =
&\begin{bmatrix}
I_{-1}^{(1)} \\
I_{-1}^{(2)} \\
I_{-1}^{(3)} \\
I_{-1}^{(4)} \\
I_0^{(1)} \\
I_0^{(2)} \\
I_0^{(3)} \\
I_0^{(4)} \\
I_{1}^{(1)} \\
I_{1}^{(2)} \\
I_{1}^{(3)} \\
I_{1}^{(4)} \\
\end{bmatrix}
+
\left[
\begin{array}{c|c|c}
\begin{matrix}
0 & 0 & 0 & 0 \\
0 & Z & -Z & 1 \\
0 & -Z & Z & 0 \\
0 & -1 & 0 & 0 \\
\end{matrix} & 0 & 0 \\ \hline
0 &
\begin{matrix}
0 & 0 & 0 & 0 \\
0 & Z & -Z & 1 \\
0 & -Z & Z & 0 \\
0 & -1 & 0 & 0 \\
\end{matrix} & 0 \\ \hline
0 & 0 &
\begin{matrix}
0 & 0 & 0 & 0 \\
0 & Z & -Z & 1 \\
0 & -Z & Z & 0 \\
0 & -1 & 0 & 0 \\
\end{matrix} \\
\end{array}
\right]
\begin{bmatrix}
V_{-1}^{(1)} \\
V_{-1}^{(2)} \\
V_{-1}^{(3)} \\
I_{-1}^{(L)} \\
V_{0}^{(1)} \\
V_{0}^{(2)} \\
V_{0}^{(3)} \\
I_{0}^{(L)} \\
V_{1}^{(1)} \\
V_{1}^{(2)} \\
V_{1}^{(3)} \\
I_{1}^{(L)} \\
\end{bmatrix} \\
&+
j \omega_0
\left[
\begin{array}{c|c|c}
(-1)
\begin{bmatrix}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & C & 0 \\
0 & 0 & 0 & L \\
\end{bmatrix} & 0 & 0 \\ \hline
0 &
(0)
\begin{bmatrix}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & C & 0 \\
0 & 0 & 0 & L \\
\end{bmatrix} & 0 \\ \hline
0 & 0 &
(1)
\begin{bmatrix}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & C & 0 \\
0 & 0 & 0 & L \\
\end{bmatrix} \\
\end{array}
\right]
\begin{bmatrix}
V_{-1}^{(1)} \\
V_{-1}^{(2)} \\
V_{-1}^{(3)} \\
I_{-1}^{(L)} \\
V_{0}^{(1)} \\
V_{0}^{(2)} \\
V_{0}^{(3)} \\
I_{0}^{(L)} \\
V_{1}^{(1)} \\
V_{1}^{(2)} \\
V_{1}^{(3)} \\
I_{1}^{(L)} \\
\end{bmatrix} \\
\end{aligned}
\end{equation}

This ordering matches that of [1].

Representing the linear sources

Assuming real sources with frequencies that are only multiples of the fundamental harmonic, a reasonable way to represent them in storage is with a pair of matrices

\begin{equation}\label{eqn:diodeRLCSample:360}
\begin{bmatrix}
\BI \sim \BB \Bomega
\end{bmatrix}.
\end{equation}

If \( R \) is the dimension of \(\BG\) and \( \BC \), then \( \BB \) is a \( R \times S \) dimension matrix, where \( S \) is the sum of

1, if there are any DC sources, plus
2 times the number of unique frequency sources.

For example, if there is a DC source and one AC source with frequency \( \nu \), then for column vectors \( \Bb_i \) this pair is of the form

\begin{equation}\label{eqn:diodeRLCSample:380}
\BU \Bomega =
\begin{bmatrix}
\Bb_{-1} & \Bb_0 & \Bb_1
\end{bmatrix}
\begin{bmatrix}
– 2 \pi \nu \\
0 \\
2 \pi \nu
\end{bmatrix}.
\end{equation}

This representation produces the time domain representation exactly when there are only DC sources, and can be used to construct the Fourier coefficients by inspection when there are AC sources. For example, for \( N = 1 \) in the example above, the Fourier coefficent vector is

\begin{equation}\label{eqn:diodeRLCSample:400}
\BI
=
\begin{bmatrix}
\Bb_{-1} \\
\Bb_{0} \\
\Bb_{1} \\
\end{bmatrix}.
\end{equation}

If \( N = 2 \) was used, then we would have instead

\begin{equation}\label{eqn:diodeRLCSample:420}
\BI
=
\begin{bmatrix}
\Bzero \\
\Bb_{-1} \\
\Bb_{0} \\
\Bb_{1} \\
\Bzero \\
\end{bmatrix}.
\end{equation}

Representing non-linear sources

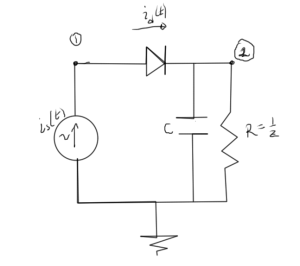
The time domain MNA fig. 1.

fig. 1. Simple diode circuit

With \( Z = 1/R, Z_g = 1/R_g \), the KCL equations are

\( \lr{ v_1 – v_2 } Z_s = i_s – i_d \)
\( \lr{ v_2 – v_1 } Z_s + v_2 Z_g = -i_s + i_d \)

Using the model \( i_d = I^{(0)} \lr{ e^{ (v_1 – v_2)/V_T } – 1 } \), with source \( i_s = I^{(s)} \cos( \omega_0 t ) \),
this has the block matrix form

\begin{equation}\label{eqn:diodeRLCSample:580}
\BG =
\begin{bmatrix}
Z_s & -Z_s \\
-Z_s & Z_s + Z_g \\
\end{bmatrix}, \qquad
\Bx =
\begin{bmatrix}
v_1(t) \\
v_2(t) \\
\end{bmatrix}
\end{equation}
\begin{equation}\label{eqn:diodeRLCSample:600}
\BB =
\begin{bmatrix}
I^{(s)}/2 & -I^{(0)} & I^{(s)}/2 \\
-I^{(s)}/2 & I^{(0)} & -I^{(s)}/2
\end{bmatrix}, \qquad
\Bu(t) =
\begin{bmatrix}
e^{-j \omega_0 t} \\
1 \\
e^{j \omega_0 t}
\end{bmatrix}
\end{equation}
\begin{equation}\label{eqn:diodeRLCSample:620}
\BD
=
\begin{bmatrix}
I^{(0)} \\
-I^{(0)}
\end{bmatrix}, \qquad
\Bw(t) = e^{(v_1(t) – v_2(t))/V_T}.
\end{equation}

If \( E_n \) is the nth DFT coefficient for \( e(t) = e^{(v_1(t) – v_2(t))/V_T} \), then the DFT equations for the \( N = 1 \) DFT is

\begin{equation}\label{eqn:diodeRLCSample:640}
\begin{aligned}
\lr{ V_{-1}^{(1)} – V_{-1}^{(2)} } Z_s &= I^{(s)}/2 – I^{(0)} E_{-1} \\
\lr{ V_{-1}^{(2)} – V_{-1}^{(1)} } Z_s + V_{-1}^{(2)} Z_g &= -I^{(s)}/2 + I^{(0)} E_{-1} \\
\lr{ V_{0}^{(1)} – V_{0}^{(2)} } Z_s &= I^{(0)} – I^{(0)} E_{0} \\
\lr{ V_{0}^{(2)} – V_{0}^{(1)} } Z_s + V_{0}^{(2)} Z_g &= -I^{(0)} + I^{(0)} E_{0} \\
\lr{ V_{1}^{(1)} – V_{1}^{(2)} } Z_s &= I^{(s)}/2 – I^{(0)} E_{1} \\
\lr{ V_{1}^{(2)} – V_{1}^{(1)} } Z_s + V_{1}^{(2)} Z_g &= -I^{(s)}/2 + I^{(0)} E_{1}
\end{aligned}
\end{equation}

Let \( \Bb = [ \Bb_{-1}\, \Bb_0\, \Bb_1 ] \), and \( \BD = [ \Bd_1 ] \). The block matrix equivalent form, by inspection, is

\begin{equation}\label{eqn:diodeRLCSample:660}
\begin{bmatrix}
\BG & 0 & 0 \\
0 & \BG & 0 \\
0 & 0 & \BG
\end{bmatrix}
\begin{bmatrix}
V_{-1}^{(1)} \\
V_{-1}^{(2)} \\
V_{0}^{(1)} \\
V_{0}^{(2)} \\
V_{1}^{(1)} \\
V_{1}^{(2)}
\end{bmatrix}
=
\begin{bmatrix}
\Bb_{-1} \\
\Bb_{0} \\
\Bb_{1} \\
\end{bmatrix}
+
\begin{bmatrix}
\Bd_1 E_{-1} \\
\Bd_1 E_{0} \\
\Bd_1 E_{1}
\end{bmatrix}.
\end{equation}

This shows the stamping pattern required to form the non-linear portion of the Harmonic balance equations. The general pattern can be written as

\begin{equation}\label{eqn:diodeRLCSample:820}
\boxed{
\mathcal{G} \BV = \BI + \mathcal{I}(\BV),
}
\end{equation}

Here \( \mathcal{G} \) is block diagonal, and in general has blocks of \( \BG + j \omega_0 n \BC \). The matrix \( \BI \) was generated from the Fourier coeffients of all the linear sources, and \( \mathcal{I}(\BV) \) encodes all the non-linear contributions to the system.

More general non-linear structure, for multiple diodes

For the diode exponentials, these non-linear term will be of the form

\begin{equation}\label{eqn:diodeRLCSample:680}
\BD \Bw(t)
=
\begin{bmatrix}
\Bd_1 & \Bd_2 & \cdots & \Bd_S
\end{bmatrix}
\begin{bmatrix}
w_1(t) \\
w_2(t) \\
\vdots \\
w_S(t) \\
\end{bmatrix},
\end{equation}

where \( w_i(t) = \exp( (v_{i,1}(t) – v_{i,2}(t))/V_{T,i} ) \). If the DFT coordinates of these functions are \( E_n^{(i)} \), then the frequency domain representation is

\begin{equation}\label{eqn:diodeRLCSample:700}
\mathcal{I}(\BV)
=
\sum_{i = 1}^S
\begin{bmatrix}
\Bd_i E_{-N}^{(i)} \\
\Bd_i E_{1-N}^{(i)} \\
\vdots \\
\Bd_i E_{N-1}^{(i)} \\
\Bd_i E_{N}^{(i)} \\
\end{bmatrix}.
\end{equation}

This is a \( R (2 N + 1) \times 1 \) matrix, as expected.

The computation of these DFT coordinates is a bit messy since they are time dependent, and thus dependent on the (unknown) values of \( V_n^{(1)} \). Consider the above circuit as an example where we have

\begin{equation}\label{eqn:diodeRLCSample:720}
w(t) = \exp\lr{ (v_1(t) – v_2(t))/V_T }.
\end{equation}

The DFT inverse is

\begin{equation}\label{eqn:diodeRLCSample:740}
E_n = \sum_{k=-N}^N \exp\lr{ (v_1(t_k) – v_2(t_k))/V_T } e^{-j \omega_0 n t_k }.
\end{equation}

With \( \BE = ( E_{-N}, E_{1-N}, \cdots, E_{N-1}, E_N ) \), this is

\begin{equation}\label{eqn:diodeRLCSample:760}
\BE =
\inv{2 N + 1} \overline{{\BF}}
\begin{bmatrix}
\exp\lr{ (v_{-N}^{(1)} – v_{-N}^{(2)})/v_T } \\
\exp\lr{ (v_{1-N}^{(1)} – v_{1-N}^{(2)})/v_T } \\
\vdots \\
\exp\lr{ (v_{N-1}^{(1)} – v_{N-1}^{(2)})/v_T } \\
\exp\lr{ (v_{N}^{(1)} – v_{N}^{(2)})/v_T } \\
\end{bmatrix}
=
\inv{2 N + 1} \overline{{\BF}}
\begin{bmatrix}
\exp\lr{ {[\BF (\BV^{(1)} – \BV^{(2)})/v_T]}_{-N} } \\
\exp\lr{ {[\BF (\BV^{(1)} – \BV^{(2)})/v_T]}_{1-N} } \\
\vdots \\
\exp\lr{ {[\BF (\BV^{(1)} – \BV^{(2)})/v_T]}_{N-1} } \\
\exp\lr{ {[\BF (\BV^{(1)} – \BV^{(2)})/v_T]}_{N} }
\end{bmatrix}.
\end{equation}

With the introduction a term by term exponentiation operator

\begin{equation}\label{eqn:diodeRLCSample:780}
\exp[ \Bx ] =
\begin{bmatrix}
\exp(x_1) \\
\exp(x_2) \\
\vdots \\
\end{bmatrix},
\end{equation}

this one Fourier coefficient vector is

\begin{equation}\label{eqn:diodeRLCSample:800}
\BE =
\inv{2 N + 1} \overline{{\BF}}
\exp[ \BF (\BV^{(1)} – \BV^{(2)})/v_T ].
\end{equation}

This is now completely expressed in terms of the unknown Fourier component vectors, each a subset of the aggreggated “voltage”, range selectable with the Matlab operation \( \BV^{(i)} = \BV(i:R:end) \).

Newton’s method

In order to solve the system, Newton’s method on the Fourier coeffients is required. Solutions to \( \mathcal{F}(\BV) = 0 \) are sought, where

\begin{equation}\label{eqn:diodeRLCSample:840}
\mathcal{F}(\BV) = \mathcal{G} \BV – \BI – \mathcal{I}(\BV).
\end{equation}

Here the sources current vector DFT coordinates have been split into the linear contributions \( \BI \) and nonlinear contributions \( \mathcal{I} \) defined by \ref{eqn:diodeRLCSample:700}.

Working with ones-indexed coordinates of \( \BV = [V_k]_k \), where \( k \in [1, R(2 N + 1) ] \), the Jacobian is

\begin{equation}\label{eqn:diodeRLCSample:860}
\BJ = \mathcal{G} – {[ \PDi{V_s}{\mathcal{I}_r} ]}_{rs}.
\end{equation}

To calculate these partials we need the partials of the coordinates of \( \BE \) of
\ref{eqn:diodeRLCSample:800}. The kth coordinate of \( \BV^{(1)}, \BV^{(2)} \) in terms of the coordinates of the \( R(2 N + 1) \) vector of unknowns \( \BV \) are

\begin{equation}\label{eqn:diodeRLCSample:880}
\begin{aligned}
[\BV^{(1)}]_k &= V_{1 + (k-1) R} \\
[\BV^{(2)}]_k &= V_{2 + (k-1) R}
\end{aligned}
\end{equation}

Using summation convention, with sums over any repeated indexes implied, those coordinates are

\begin{equation}\label{eqn:diodeRLCSample:900}
E_r =
\inv{2 N + 1} \overline{{F}}_{r a}
\exp\lr{ F_{ab}
(
V_{1 + (b-1) R} –
V_{2 + (b-1) R}
)/v_T }.
\end{equation}

The partials now follow immediately

\begin{equation}\label{eqn:diodeRLCSample:920}
\PD{V_s}{E_r} =
\inv{2 N + 1} \inv{v_T} \overline{{F}}_{r a} F_{ab}
\exp\lr{ F_{ab}
(
V_{1 + (b-1) R} –
V_{2 + (b-1) R}
)/v_T }
\lr{
\delta_{s,1 + (b-1) R} –
\delta_{s,2 + (b-1) R}
}.
\end{equation}

Generalization

To generalize this, suppose that the diode exponential was associated with voltages spanning nodes \( m, n\) so that

\begin{equation}\label{eqn:diodeRLCSample:980}
\BE =
\inv{2 N + 1} \overline{{\BF}}
\exp[ \BF (\BV^{(m)} – \BV^{(n)})/v_T ].
\end{equation}

In this case, the coordinates of the physical “voltages” are

\begin{equation}\label{eqn:diodeRLCSample:1020}
\begin{aligned}
[\BV^{(m)}]_k &= V_{m + (k-1) R} \\
[\BV^{(n)}]_k &= V_{n + (k-1) R}
\end{aligned},
\end{equation}

\begin{equation}\label{eqn:diodeRLCSample:1040}
E_r =
\inv{2 N + 1} \overline{{F}}_{r a}
\exp\lr{ F_{ab}
(
V_{m + (b-1) R} –
V_{n + (b-1) R}
)/v_T }.
\end{equation}

The Jacobian partials are

\begin{equation}\label{eqn:diodeRLCSample:1060}
\PD{V_s}{E_r} =
\inv{2 N + 1} \inv{v_T} \overline{{F}}_{r a} F_{ab}
\exp\lr{ F_{ab}
(
V_{m + (b-1) R} –
V_{n + (b-1) R}
)/v_T }
\lr{
\delta_{s,m + (b-1) R} –
\delta_{s,n + (b-1) R}
}.
\end{equation}

Note that this Jacobian

\begin{equation}\label{eqn:diodeRLCSample:1080}
\BJ_\BE =
{
\begin{bmatrix}
\PD{V_s}{E_r}
\end{bmatrix}}_{rs}
\end{equation}

is a \( (2 N + 1) \times R(2N + 1) \) matrix.

The full Jacobian of \( \mathcal{I}(\BV) \) is

\begin{equation}\label{eqn:diodeRLCSample:1120}
\BJ_{\mathcal{I}}(\BV)
=
\sum_{i = 1}^S
\begin{bmatrix}
\Bd_i \PD{\BV}{E_{-N}^{(i)}} \\
\Bd_i \PD{\BV}{E_{1-N}^{(i)}} \\
\vdots \\
\Bd_i \PD{\BV}{E_{N-1}^{(i)}} \\
\Bd_i \PD{\BV}{E_{N}^{(i)}} \\
\end{bmatrix}.
\end{equation}

Where \( \PDi{\BV}{E_{k}^{(i)}} \) is the kth row of \( \BJ_{\BE^{(i)}} \). The complete Jacobian is

\begin{equation}\label{eqn:diodeRLCSample:1100}
\BJ = \mathcal{G} – \BJ_{\mathcal{I}}(\BV).
\end{equation}

References

Giannini and Giorgio Leuzzi. Nonlinear Microwave Circuit Design. Wiley Online Library, 2004.

A sample diode RLC circuit

December 5, 2014 ece1254 diode model, discrete Fourier transform, ece1254, MNA equations, phasor, RLC circuit, time dependent

[Click here for a PDF of this post with nicer formatting]

To get a feel for how to generate the MLN equations for a circuit that has both RLC and non-linear components, consider the circuit of fig. 1.

fig. 1. An RLC circuit with a diode.

The KCL equations for this circuit are

\( 0 = i_s – i_d \)
\( i_L + \frac{v_2 – v_3}{R} = i_d \)
\( \frac{v_3 – v_2}{R} + C \frac{dv_3}{dt} = 0 \)
\( -v_2 + L \frac{d i_L}{dt} = 0 \)
\( i_d = I_0 \lr{ e^{(v_1 – v_2)/v_T} – 1} \)

FIXME: for the diode, is that the right voltage sign with respect to the current direction?

With \( Z = 1/R \), these can be put into the standard MLN matrix form as

\begin{equation}\label{eqn:diodeRLCSample:20}
\begin{bmatrix}
0 & 0 & 0 & 0 \\
0 & Z & -Z & 1 \\
0 & -Z & Z & 0 \\
0 & -1 & 0 & 0 \\
\end{bmatrix}
\begin{bmatrix}
v_1 \\
v_2 \\
v_3 \\
i_L \\
\end{bmatrix}
+
\begin{bmatrix}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & C & 0 \\
0 & 0 & 0 & L \\
\end{bmatrix}
{\begin{bmatrix}
v_1 \\
v_2 \\
v_3 \\
i_L \\
\end{bmatrix}}’
=
\begin{bmatrix}
I_0 & 1 \\
-I_0 & 0 \\
0 & 0 \\
0 & 0 \\
\end{bmatrix}
\begin{bmatrix}
1 \\
i_s(t) \\
\end{bmatrix}
+
\begin{bmatrix}
-I_0 \\
I_0 \\
0 \\
0 \\
\end{bmatrix}
\begin{bmatrix}
e^{(v_2 – v_3)/v_T}
\end{bmatrix}
\end{equation}

Let’s write this as

\begin{equation}\label{eqn:diodeRLCSample:40}
\BG \BX(t) + \BC \dot{\BX}(t) = \BB \Bu(t) + \BD \Bw(t).
\end{equation}

Here \( \Bu(t) \) collects up all the unique signature sources (for example sources with each different frequency in the system), and \( \Bw(t) \) is a vector of all the unique non-linear (time dependent) terms.

Assuming a bandwidth limited periodic source we know how to express any of the time dependent variables \( v_1, … \) in terms of their (discrete) Fourier transforms. Suppose that

the Fourier coefficients for \( v_a(t), u_b(t), w_c(t) \) are given by

\begin{equation}\label{eqn:diodeRLCSample:60}
\begin{aligned}
v_a(t) &= \sum_{n = -N}^N V_n^{(a)} e^{j \omega_0 n t} \\
u_b(t) &= \sum_{n = -N}^N U_n^{(b)} e^{j \omega_0 n t} \\
w_c(t) &= \sum_{n = -N}^N W_n^{(c)} e^{j \omega_0 n t}.
\end{aligned}
\end{equation}

For example, in this circuit, if the source was zero phase signal at the fundamental frequency of our Fourier basis (\( i_s(t) = e^{j \omega_0 t} \)), the only non-zero Fourier components \( U_n^{(a)} \) would be \( U_0^{(1)} = 1, U_1^{(2)} = 1 \).

Equation \ref{eqn:diodeRLCSample:40} then becomes

\begin{equation}\label{eqn:diodeRLCSample:80}
0 = \sum_{n=-N}^N
e^{j n \omega_0 t}
\lr{
\lr{
\BG + j \omega_0 n \BC
}
\begin{bmatrix}
V_n^{(1)} \\
V_n^{(2)} \\
\vdots
\end{bmatrix}
– \BB
\begin{bmatrix}
U_n^{(1)} \\
U_n^{(2)} \\
\end{bmatrix}
– \BD
\begin{bmatrix}
W_n^{(1)} \\
\end{bmatrix}
}
\end{equation}

The time dependence in the linear terms is nicely taken of by this transformation to the frequency domain. However, we have a fairly messy structure with sums of Fourier components instead of the nice Fourier component vectors that we see in \S A.4 of [1]. That reference does consider multivariable problems like this one, so it looks like fully digesting that methodology is the next step.

References

Giannini and Giorgio Leuzzi. Nonlinear Microwave Circuit Design. Wiley Online Library, 2004.

Matrix form for discrete time Fourier transform

December 4, 2014 ece1254 discrete Fourier transform, ece1254, matrix

[Click here for a PDF of this post with nicer formatting]

Matrix form

The discrete time Fourier transform has been seen to have the form

\begin{equation}\label{eqn:discreteFourierMatrixForm:200}
x_k = \sum_{n = -N}^N X_n e^{ 2 \pi j n k /(2 N + 1)}
\end{equation}
\begin{equation}\label{eqn:discreteFourierMatrixForm:220}
X_n = \inv{2 N + 1} \sum_{k = -N}^N x_k e^{- 2 \pi j n k /(2 N + 1)}.
\end{equation}

A matrix representation of this form is desired. Let

\begin{equation}\label{eqndiscreteFourierMatrixForm:240}
\Bx =
\begin{bmatrix}
x_N \\
\vdots \\
x_0 \\
\vdots \\
x_{-N}
\end{bmatrix}
\end{equation}
\begin{equation}\label{eqndiscreteFourierMatrixForm:260}
\BX =
\begin{bmatrix}
X_N \\
\vdots \\
X_0 \\
\vdots \\
X_{-N}
\end{bmatrix}
\end{equation}

\ref{eqn:discreteFourierMatrixForm:200} written out in full is
\begin{equation}\label{eqn:discreteFourierMatrixForm:280}
\begin{aligned}
x_k
&= X_N e^{ 2 \pi j N k /(2 N + 1)} \\
&+ X_{N-1} e^{ 2 \pi j \lr{N-1} k /(2 N + 1)} \\
&+ \cdots \\
&+ X_0 \\
&+ \cdots \\
&+ X_{1-N} e^{ -2 \pi j \lr{N-1} k /(2 N + 1)} \\
&+ X_{-N} e^{ -2 \pi j N k /(2 N + 1)}.
\end{aligned}
\end{equation}

With \( \alpha = e^{ 2 \pi j /(2 N + 1) } \) the matrix form is

\begin{equation}\label{eqn:discreteFourierMatrixForm:300}
\Bx =
\begin{bmatrix}
\alpha^{ N N } & \alpha^{ \lr{N-1} N } & \cdots & 1 & \cdots & \alpha^{ -\lr{N-1} N } & \alpha^{ -N N } \\
\alpha^{ N \lr{N-1} } & \alpha^{ \lr{N-1} \lr{N-1} } & \cdots & 1 & \cdots & \alpha^{ -\lr{N-1} \lr{N-1} } & \alpha^{ -N \lr{N-1} } \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
1 & 1 & 1 & 1 & 1 & 1 & 1 \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
\alpha^{ -N \lr{N-1} } & \alpha^{ -\lr{N-1} \lr{N-1} } & \cdots & 1 & \cdots & \alpha^{ {N-1} \lr{N-1} } & \alpha^{ N \lr{N-1} } \\
\alpha^{ -N N } & \alpha^{ -N N } & \cdots & 1 & \cdots & \alpha^{ \lr{N-1} N } & \alpha^{ N N } \\
\end{bmatrix}
\BX
\end{equation}

Similarily, from \ref{eqn:discreteFourierMatrixForm:220}, the inverse relation expands out to

\begin{equation}\label{eqn:discreteFourierMatrixForm:320}
\begin{aligned}
( 2 N + 1 ) X_n
&= x_N e^{- 2 \pi j n N /(2 N + 1)} \\
&+ x_{N-1} e^{- 2 \pi j n \lr{N-1}/(2 N + 1)} \\
&\cdots \\
&+ x_0 \\
&\cdots \\
&+ x_{1-N} e^{ 2 \pi j n \lr{ N-1 }/(2 N + 1)} \\
&+ x_{-N} e^{ 2 \pi j n N/(2 N + 1)},
\end{aligned}
\end{equation}

with a matrix form of

\begin{equation}\label{eqn:discreteFourierMatrixForm:340}
( 2 N + 1 ) \BX =
\begin{bmatrix}
\alpha^{- N N } & \alpha^{- N \lr{N-1}} &\cdots & 1 &\cdots & \alpha^{ N \lr{ N-1 }} & \alpha^{ N N} \\
\alpha^{- \lr{N-1} N } & \alpha^{- \lr{N-1} \lr{N-1}} &\cdots & 1 &\cdots & \alpha^{ \lr{N-1} \lr{ N-1 }} & \alpha^{ \lr{N-1} N} \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
1 & 1 & 1 & 1 & 1 & 1 & 1 \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
\alpha^{\lr{N-1} N } & \alpha^{ \lr{N-1} \lr{N-1}} &\cdots & 1 &\cdots & \alpha^{ -\lr{N-1} \lr{ N-1 }} & \alpha^{ -\lr{N-1} N} \\
\alpha^{ N N } & \alpha^{ N \lr{N-1}} &\cdots & 1 &\cdots & \alpha^{ -N \lr{ N-1 }} & \alpha^{ -N N} \\
\end{bmatrix}
\end{equation}

Lettting

\begin{equation}\label{eqn:discreteFourierMatrixForm:360}
\BF =
\begin{bmatrix}
\alpha^{ N N } & \alpha^{ \lr{N-1} N } & \cdots & 1 & \cdots & \alpha^{ -\lr{N-1} N } & \alpha^{ -N N } \\
\alpha^{ N \lr{N-1} } & \alpha^{ \lr{N-1} \lr{N-1} } & \cdots & 1 & \cdots & \alpha^{ -\lr{N-1} \lr{N-1} } & \alpha^{ -N \lr{N-1} } \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
1 & 1 & 1 & 1 & 1 & 1 & 1 \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
\alpha^{ -N \lr{N-1} } & \alpha^{ -\lr{N-1} \lr{N-1} } & \cdots & 1 & \cdots & \alpha^{ {N-1} \lr{N-1} } & \alpha^{ N \lr{N-1} } \\
\alpha^{ -N N } & \alpha^{ -N N } & \cdots & 1 & \cdots & \alpha^{ \lr{N-1} N } & \alpha^{ N N } \\
\end{bmatrix},
\end{equation}

the discrete transform pair has the following compactly matrix representation

\begin{equation}\label{eqn:discreteFourierMatrixForm:380}
\Bx = \BF \BX
\end{equation}
\begin{equation}\label{eqn:discreteFourierMatrixForm:400}
\BX = \inv{2 N + 1} \overline{{\BF}} \Bx,
\end{equation}

where \( \overline{{\BF}} \) is the complex conjugate of \( \BF \).

ece1254

Marks are in for Winter 2016

Like this:

A matrix formulation of the Harmonic Balance method non-linear currents

Jacobian

Newton’s method solution

Like this:

Development of Harmonic balance equations (considering a sample diode RLC circuit)

Block matrix form, with physical parameter ordering

Block matrix form, with frequency ordering

Representing the linear sources

Representing non-linear sources

More general non-linear structure, for multiple diodes

Newton’s method

Generalization

References

Like this:

A sample diode RLC circuit

References

Like this:

Matrix form for discrete time Fourier transform

Matrix form

References

Like this:

Pages

Categories

Recent Posts

Archives

Meta

Categories

Recent Posts

Archives

ece1254

Marks are in for Winter 2016

Share this:

Like this:

A matrix formulation of the Harmonic Balance method non-linear currents

Jacobian

Newton’s method solution

Share this:

Like this:

Development of Harmonic balance equations (considering a sample diode RLC circuit)

Block matrix form, with physical parameter ordering

Block matrix form, with frequency ordering

Representing the linear sources

Representing non-linear sources

More general non-linear structure, for multiple diodes

Newton’s method

Generalization

References

Share this:

Like this:

A sample diode RLC circuit

References

Share this:

Like this:

Matrix form for discrete time Fourier transform

Matrix form

References

Share this:

Like this:

Pages

Categories

Recent Posts

Tags

Archives

Meta

Categories

Recent Posts

Tags

Archives