[Click here for a PDF version of this post]
I saw a funky looking formula for the mth Fibonacci number on twitter
\begin{equation}\label{eqn:fibonacci_sinh:20}
F_m = \frac{2}{\sqrt{5} i^m} \sinh\lr{ m \ln\lr{i\phi} },
\end{equation}
where
\begin{equation}\label{eqn:fibonacci_sinh:60}
\phi = \frac{ 1 + \sqrt{5} }{2},
\end{equation}
is the golden ratio.
This certainly doesn’t look like it’s a representation of the sequence
\begin{equation}\label{eqn:fibonacci_sinh:40}
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, \cdots
\end{equation}
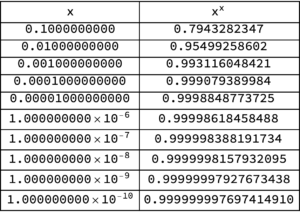
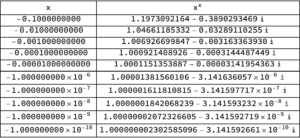
We can verify that it works in Mathematica, as seen in fig. 1.
Recall that we previously found this formula for the mth Fibonacci number
\begin{equation}\label{eqn:fibonacci_sinh:80}
F_m = \inv{\sqrt{5}} \lr{ \phi^m – { \bar{\phi}}^m },
\end{equation}
where \( \bar{\phi} \) is the conjugate of the golden ratio
\begin{equation}\label{eqn:fibonacci_sinh:100}
\bar{\phi} = \frac{ 1 – \sqrt{5} }{2}.
\end{equation}
Let’s see how these are equivalent. First observe that the golden conjugate is easily related to the inverse of the golden ratio
\begin{equation}\label{eqn:fibonacci_sinh:120}
\begin{aligned}
\inv{\phi}
&=
\frac{2}{1 + \sqrt{5}} \\
&=
\frac{2\lr{ 1 – \sqrt{5}} }{1^2 – \lr{\sqrt{5}}^2 } \\
&=
-\frac{1 – \sqrt{5} }{2} \\
&=
-\bar{\phi}.
\end{aligned}
\end{equation}
Substitution gives
\begin{equation}\label{eqn:fibonacci_sinh:140}
F_m = \inv{\sqrt{5}} \lr{ \phi^m – \lr{\frac{-1}{\phi}}^m }.
\end{equation}
Multiplying by \( i^m \), we have
\begin{equation}\label{eqn:fibonacci_sinh:160}
\begin{aligned}
i^m F_m
&= \inv{\sqrt{5}} \lr{ i^m \phi^m – \inv{(-i)^m} \lr{\frac{-1}{\phi}}^m } \\
&= \inv{\sqrt{5}} \lr{ \lr{ i \phi} ^m – \lr{i \phi}^{-m} } \\
\end{aligned}
\end{equation}
We can write any exponent in terms of \( e \)
\begin{equation}\label{eqn:fibonacci_sinh:180}
a^m = e^{\ln a^m} = e^{m \ln a},
\end{equation}
so
\begin{equation}\label{eqn:fibonacci_sinh:200}
\begin{aligned}
i^m F_m
&= \inv{\sqrt{5}} \lr{ e^{m \ln \lr{ i \phi}} – e^{-m \ln\lr{i \phi} } } \\
&= \inv{\sqrt{5}} 2 \sinh\lr{ m \ln \lr{ i \phi } },
\end{aligned}
\end{equation}
as we wanted to show. It’s a bit strange looking, but we see why it works.