[Click here for a PDF version of this post]
In the LinkedIn Pre-University Geometric Algebra group, James presents a problem from the MindYourDecisions youtube channel Impossible Viral Problem, as a candidate for solution using geometric algebra.
I tried this out and found a couple ways to solve it. One of those I’ll detail here. I have to admit that part of the reason that I wanted to solve this is that the figure in the beginning of the video really bugged me. The triangle that was inscribed in the circle didn’t have any of the length properties from the problem. I could do much better with a sloppy freehand sketch, but to do a good figure, you have to actually solve for the vertexes of the triangle (once you do that, the area is easy to figure out.)
Formulating the problem.
Having solved the problem, the geometry of the problem is illustrated in fig. 1.
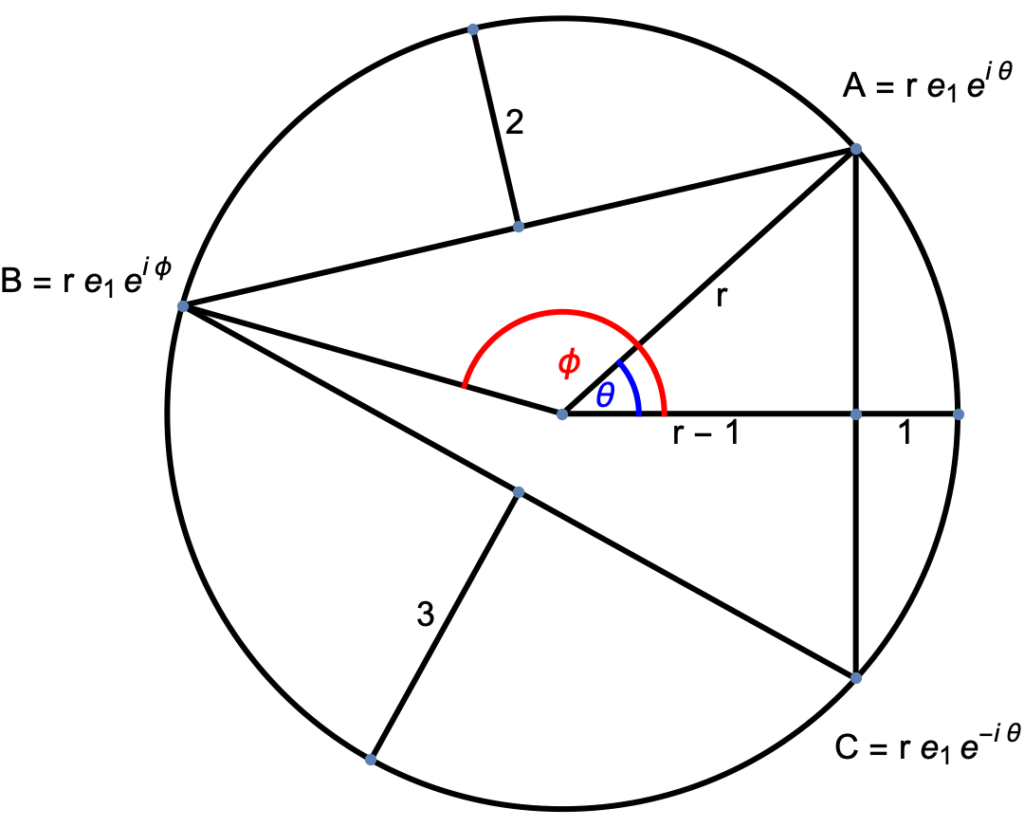
fig. 1. Inscribed triangle in circle.
I set up the problem so that the \( A,C \) triangle vertices were symmetric with respect to the x-axis, and the \(B \) vertex located elsewhere. I can describe those algebraically as
\begin{equation}\label{eqn:inscribedTriangleProblem:20}
\begin{aligned}
\BA &= r \Be_1 e^{i\theta} \\
\BC &= r \Be_1 e^{-i\theta} \\
\BB &= r \Be_1 e^{i\phi},
\end{aligned}
\end{equation}
where the radius \( r \) and two angles \( \theta, \phi \) are to be determined, and \( i = \Be_1 \Be_1\) the pseudoscalar for the \(x-y\) plane.
The vector pointing to the midpoint of the upper triangular face is given by the average of the \( \BA, \BB \) vectors, which can be seen from
\begin{equation}\label{eqn:inscribedTriangleProblem:40}
\BA + \frac{\BB – \BA}{2} = \frac{\BA + \BB}{2},
\end{equation}
and similarly, the midpoint of the lower face is found at
\begin{equation}\label{eqn:inscribedTriangleProblem:60}
\BC + \frac{\BB – \BC}{2} = \frac{\BB + \BC}{2},
\end{equation}
The problem tells us that the respective lengths of those vectors from the origin are \( r-2, r – 3\) respectively, so
\begin{equation}\label{eqn:inscribedTriangleProblem:80}
\begin{aligned}
r – 2 &= \inv{2} \Abs{ \BA + \BB } \\
r – 3 &= \inv{2} \Abs{ \BB + \BC },
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:inscribedTriangleProblem:100}
\begin{aligned}
(r – 2)^2 &= \frac{r^2}{4} \lr{ \Be_1 e^{i\theta} + \Be_1 e^{i\phi} }^2 \\
(r – 3)^2 &= \frac{r^2}{4} \lr{ \Be_1 e^{i\phi} + \Be_1 e^{-i\theta} }^2 \\
\end{aligned}
\end{equation}
Finally, since the midpoint of the right edge is found at \( (r-1)\Be_1 \), it is clear that
\begin{equation}\label{eqn:inscribedTriangleProblem:120}
\frac{r-1}{r} = \cos\theta,
\end{equation}
or
\begin{equation}\label{eqn:inscribedTriangleProblem:140}
r = \inv{1 – \cos\theta}.
\end{equation}
This leaves us with three equations and three unknowns. Unfortunately, these are rather non-linear equations. In the video, a direct method of solving equivalent equations was demonstrated, but I picked the lazy route, and used Mathematica’s NSolve routine, solving for \( r,\theta, \phi\) numerically. Since NSolve has intrinsic complex number support, I made the following substitutions:
\begin{equation}\label{eqn:inscribedTriangleProblem:160}
\begin{aligned}
z &= e^{i\theta} \\
w &= e^{i\phi},
\end{aligned}
\end{equation}
and then plugged those into our relations above, after expanding the squares, to find
\begin{equation}\label{eqn:inscribedTriangleProblem:180}
\begin{aligned}
\lr{ \Be_1 e^{i\theta} + \Be_1 e^{i\phi} }^2
&=
2 + \Be_1 e^{i\theta} \Be_1 e^{i\phi} + \Be_1 e^{i\phi} \Be_1 e^{i\theta} \\
&=
2 + e^{-i\theta} \Be_1^2 e^{i\phi} + e^{-i\phi} \Be_1^2 e^{i\theta} \\
&=
2 + e^{-i\theta} \Be_1^2 e^{i\phi} + e^{-i\phi} \Be_1^2 e^{i\theta} \\
&=
2 + \frac{w}{z} + \frac{z}{w},
\end{aligned}
\end{equation}
and
\begin{equation}\label{eqn:inscribedTriangleProblem:200}
\begin{aligned}
\lr{ \Be_1 e^{i\phi} + \Be_1 e^{-i\theta} }^2
&=
2 + \Be_1 e^{i\phi} \Be_1 e^{-i\theta} + \Be_1 e^{-i\theta} \Be_1 e^{i\phi} \\
&=
2 + e^{-i\phi} e^{-i\theta} + e^{ i\theta} e^{i\phi} \\
&=
2 + w z + \inv{w z}.
\end{aligned}
\end{equation}
This gives us
\begin{equation}\label{eqn:inscribedTriangleProblem:220}
\begin{aligned}
4 \lr{ \frac{r – 2 }{r} }^2 &= 2 + \frac{w}{z} + \frac{z}{w} \\
4 \lr{ \frac{r – 3 }{r} }^2 &= 2 + w z + \inv{w z},
\end{aligned}
\end{equation}
where
\begin{equation}\label{eqn:inscribedTriangleProblem:240}
r = \inv{1 – \inv{2}\lr{ z + \inv{z}}}.
\end{equation}
The NSolve gave me some garbage solutions (like \(\theta = 0 \)) that must have been valid numerically, but did not encode the geometry of the problem, so I added a few additional constraints to the problem, namely
\begin{equation}\label{eqn:inscribedTriangleProblem:260}
\begin{aligned}
z \bar{z} &= 1 \\
w \bar{w} &= 1 \\
\inv{2} \lr{ z + \inv{z} } &\ne 1 \\
1/(1 – (1/2) \textrm{Re}(z + 1/z)) &> 3.
\end{aligned}
\end{equation}
This provided exactly two solutions, but when plotted, they turn out to just be mirror images of each other. After back substitution, the solution illustrated above was given by
\begin{equation}\label{eqn:inscribedTriangleProblem:280}
\begin{aligned}
r &= 3.87939 \\
\theta &= 42.078 \\
\phi &= 164.125,
\end{aligned}
\end{equation}
where these angles are in degrees, not radians.
The triangular area.
There are probably lots of formulas for the area of a triangle (that I have forgotten), but we can compute it easily by doubling the triangle, forming a parallelogram, to find
\begin{equation}\label{eqn:inscribedTriangleProblem:300}
\textrm{Area} = \inv{2} \Abs{ \lr{ \BA – \BC } \wedge {\BC – \BB } },
\end{equation}
or
\begin{equation}\label{eqn:inscribedTriangleProblem:320}
\begin{aligned}
\textrm{Area}^2
&= \frac{-1}{4} \lr{ \lr{ \BA – \BC } \wedge \lr{\BC – \BB } }^2 \\
&= \frac{-1}{4} \lr{ \BA \wedge \BC – \BA \wedge \BB + \BC \wedge \BB }^2 \\
&= \frac{-r^4}{4} \lr{\gpgradetwo{ \Be_1 e^{i\theta} \Be_1 e^{-i\theta} – \Be_1 e^{i\theta} \Be_1 e^{i\phi} + \Be_1 e^{-i\theta} \Be_1 e^{i\phi} }}^2 \\
&= \frac{-r^4}{4} \lr{\gpgradetwo{ e^{-2 i \theta} – e^{i \phi -i\theta} + e^{i\theta + i \phi} }}^2,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:inscribedTriangleProblem:340}
\textrm{Area} = \frac{r^2}{2} \Abs{ -\sin( 2 \theta ) – \sin(\phi- \theta) + \sin(\theta + \phi)}.
\end{equation}
Plugging in \( r, \theta, \phi \), we find
\begin{equation}\label{eqn:inscribedTriangleProblem:360}
\textrm{Area} = 17.1866.
\end{equation}
After computing this value, I then finally watched the original video to compare my answer, and was initially disturbed to find that this wasn’t even one of the possible values. However, that was because the problem itself, as originally stated, didn’t include the correct answer, and my worry that I’d made a mistake was unfounded, as the value I computed matched what was computed in the video (it also looks “about right” visually.)
Like this:
Like Loading...