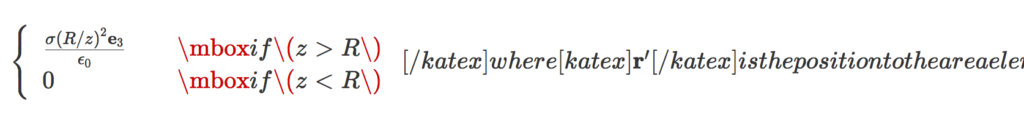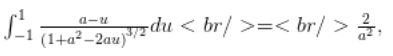In a previous post I attempted to use the katex plugin to render an old post instead of using Mathjax. It seems that was not actually rendered with KaTex, but (I think) it was rendered with the latex keyword handling in the Jetpack plugin, which I also had installed. I’ve customized the katex plugin I have installed to use a different keyword (katex instead of latex).
This is a test of KaTex, the latex rendering engine used for Khan academy. They advertise themselves as much faster than mathjax, but this speed comes with some usability issues.
Here’s a rerendering of an old post, with the latex rendered with WP-KaTeX instead of MathJax-LaTeX.
The post
Problem:
Calculate the field due to a spherical shell. The field is
[katex display=”true”]\mathbf{E} = \frac{\sigma}{4 \pi \epsilon_0} \int \frac{(\mathbf{r} – \mathbf{r}’)}{{{\left\lvert{{\mathbf{r} – \mathbf{r}’}}\right\rvert}}^3} da’,[/katex]
where [katex]\mathbf{r}'[/katex] is the position to the area element on the shell. For the test position, let [katex]\mathbf{r} = z \mathbf{e}_3[/katex].
Solution:
We need to parameterize the area integral. A complex-number like geometric algebra representation works nicely.
[katex display=”true”]\begin{aligned}\mathbf{r}’ &= R \left( \sin\theta \cos\phi, \sin\theta \sin\phi, \cos\theta \right) \\ &= R \left( \mathbf{e}_1 \sin\theta \left( \cos\phi + \mathbf{e}_1 \mathbf{e}_2 \sin\phi \right) + \mathbf{e}_3 \cos\theta \right) \\ &= R \left( \mathbf{e}_1 \sin\theta e^{i\phi} + \mathbf{e}_3 \cos\theta \right).\end{aligned}[/katex]
Here [katex]i = \mathbf{e}_1 \mathbf{e}_2[/katex] has been used to represent to horizontal rotation plane.
The difference in position between the test vector and area-element is
[katex display=”true”]\mathbf{r} – \mathbf{r}’ = \mathbf{e}_3 {\left({ z – R \cos\theta }\right)} – R \mathbf{e}_1 \sin\theta e^{i \phi},[/katex]
with an absolute squared length of
[katex display=”true”]\begin{aligned}{{\left\lvert{{\mathbf{r} – \mathbf{r}’ }}\right\rvert}}^2 &= {\left({ z – R \cos\theta }\right)}^2 + R^2 \sin^2\theta \\ &= z^2 + R^2 – 2 z R \cos\theta.\end{aligned}[/katex]
As a side note, this is a kind of fun way to prove the old “cosine-law” identity. With that done, the field integral can now be expressed explicitly
[katex display=”true”]\begin{aligned} \mathbf{E} &= \frac{\sigma}{4 \pi \epsilon_0} \int_{\phi = 0}^{2\pi} \int_{\theta = 0}^\pi R^2 \sin\theta d\theta d\phi \frac{\mathbf{e}_3 {\left({ z – R \cos\theta }\right)} – R \mathbf{e}_1 \sin\theta e^{i \phi}} { {\left({z^2 + R^2 – 2 z R \cos\theta}\right)}^{3/2} } \\ &= \frac{2 \pi R^2 \sigma \mathbf{e}_3}{4 \pi \epsilon_0} \int_{\theta = 0}^\pi \sin\theta d\theta \frac{z – R \cos\theta} { {\left({z^2 + R^2 – 2 z R \cos\theta}\right)}^{3/2} } \\ &= \frac{2 \pi R^2 \sigma \mathbf{e}_3}{4 \pi \epsilon_0} \int_{\theta = 0}^\pi \sin\theta d\theta \frac{ R( z/R – \cos\theta) } { (R^2)^{3/2} {\left({ (z/R)^2 + 1 – 2 (z/R) \cos\theta}\right)}^{3/2} } \\ &= \frac{\sigma \mathbf{e}_3}{2 \epsilon_0} \int_{u = -1}^{1} du \frac{ z/R – u} { {\left({1 + (z/R)^2 – 2 (z/R) u}\right)}^{3/2} }. \end{aligned}[/katex]
Observe that all the azimuthal contributions get killed. We expect that due to the symmetry of the problem. We are left with an integral that submits to Mathematica, but doesn’t look fun to attempt manually. Specifically
[katex display=”true”]\int_{-1}^1 \frac{a-u}{{\left({1 + a^2 – 2 a u}\right)}^{3/2}} du = \frac{2}{a^2},[/katex]
if [katex]a > 1[/katex], and zero otherwise, so
[katex display=”true”]\boxed{ \mathbf{E} = \frac{\sigma (R/z)^2 \mathbf{e}_3}{\epsilon_0} }[/katex]
for [katex]z > R[/katex], and zero otherwise.
In the problem, it is pointed out to be careful of the sign when evaluating [katex]\sqrt{ R^2 + z^2 – 2 R z }[/katex], however, I don’t see where that is even useful?
KaTex commentary
- Conditional patterns, such as:
\left\{ \begin{array}{l l} \frac{\sigma (R/z)^2 \mathbf{e}_3}{\epsilon_0} & \quad \mbox{if $ z > R $ } \\ 0 & \quad \mbox{if $ z < R $ } \end{array} \right.messed up KaTex, resulting in render errors like:
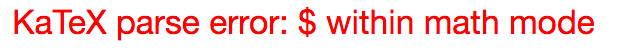
Using \( ... \) within math mode instead of $ ... $ also messed things up. Example:
\left\{ \begin{array}{l l} \frac{\sigma (R/z)^2 \mathbf{e}_3}{\epsilon_0} & \quad \mbox{if $ z > R $ } \\ 0 & \quad \mbox{if $ z < R $ } \end{array} \right.This resulted in a messed up parse like so:
It looks like it's the mbox that messes things up, and not the array itself, so \text could probably be used instead.
- The latex has to be all in one line, or else KaTex renders the newlines explicitly. Example:
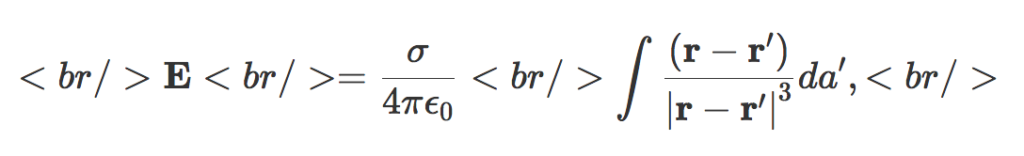
Having to condense all my latex onto a single line is one of the reasons I switched from the default wordpress latex engine to mathjax. It was annoying enough that I started paying for my wordpress hosting, and stopped posting on my old free peeterjoot.wordpress.com blog. Using KaTex and having to go back to single line latex would suck!
- The rendering looks great, just like mathjax.
- The Mathjax-Latex wordpress plugin has some support for equation labeling and references. I don't see a way to do those with the WP-KaTex plugin.
- I can have a large set of macros installed in my default.js matching a subset of what I have in my .sty files. I don't see a way to do that with the WP-KaTex plugin, but perhaps there is just no documented mechanism. KaTex itself does have a macro mechanism.
- The display isn't left justified like the wordpress latex, and looks decent.
is the position to the area element on the shell. For the test position, let 
.
has been used to represent to horizontal rotation plane.
, and zero otherwise, so
, and zero otherwise.
, however, I don’t see where that is even useful?
