[Click here for a PDF version of this post]
Problem from:
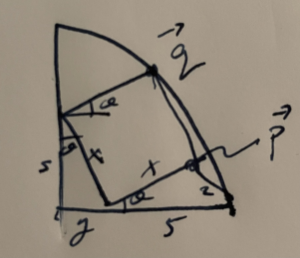
My solution (before numerical reduction), using basic trig and complex numbers, is illustrated in fig. 1.
We have
\begin{equation}\label{eqn:squareInCircle:20}
\begin{aligned}
s &= x \cos\theta \\
y &= x \sin\theta \\
p &= y + x e^{i\theta} \\
q &= i s + x e^{i\theta} \\
\Abs{q} &= y + 5 \\
\Abs{p – q} &= 2.
\end{aligned}
\end{equation}
This can be reduced to
\begin{equation}\label{eqn:squareInCircle:40}
\begin{aligned}
\Abs{ x e^{i\theta} – 5 } &= 2 \\
x \Abs{ i \cos\theta + e^{i\theta} } &= x \sin\theta + 5.
\end{aligned}
\end{equation}
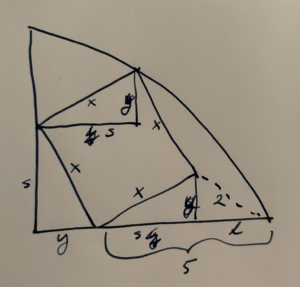
My wife figured out how to do it with just Pythagoras, as illustrated in fig. 2.
\begin{equation}\label{eqn:squareInCircle:60}
\begin{aligned}
\lr{ 5 – s }^2 + y^2 &= 4 \\
\lr{ s + y }^2 + s^2 &= \lr{ y + 5 }^2 \\
x^2 &= s^2 + y^2.
\end{aligned}
\end{equation}
Either way, the numerical solution is 4.12. The geometry looks like fig. 3.
A mathematica notebook to compute the numerical part of the problem (either way) and plot the figure to scale can be found in my mathematica github repo.