netCDF

A better 3D generalization of the Mandelbrot set.

February 9, 2021 math and physics play , , , , , , ,

I’ve been exploring 3D generalizations of the Mandelbrot set:

The iterative equation for the Mandelbrot set can be written in vector form ([1]) as:
\begin{equation}
\begin{aligned}
\Bz
&\rightarrow
\Bz \Be_1 \Bz + \Bc \\
&=
\Bz \lr{ \Be_1 \cdot \Bz }
+
\Bz \cdot \lr{ \Be_1 \wedge \Bz }
+ \Bc \\
&=
2 \Bz \lr{ \Be_1 \cdot \Bz }
–
\Bz^2\, \Be_1
+ \Bc
\end{aligned}
\end{equation}
Plotting this in 3D was an interesting challenge, but showed that the Mandelbrot set expressed above has rotational symmetry about the x-axis, which is kind of boring.

If all we require for a 3D fractal is to iterate a vector equation that is (presumably) at least quadratic, then we have lots of options. Here’s the first one that comes to mind:
\begin{equation}
\begin{aligned}
\Bz
&\rightarrow
\gpgradeone{ \Ba \Bz \Bb \Bz \Bc } + \Bd \\
&=
\lr{ \Ba \cdot \Bz } \lr{ \Bz \cross \lr{ \Bc \cross \Bz } }
+
\lr{ \Ba \cross \Bz } \lr{ \Bz \cdot \lr{ \Bc \cross \Bz } }
+ \Bd
.
\end{aligned}
\end{equation}
where we iterate starting, as usual with \( \Bz = 0 \) where \( \Bd \) is the point of interest to test for inclusion in the set. I tried this with
\begin{equation}\label{eqn:mandel3:n}
\begin{aligned}
\Ba &= (1,1,1) \\
\Bb &= (1,0,0) \\
\Bc &= (1,-1,0).
\end{aligned}
\end{equation}
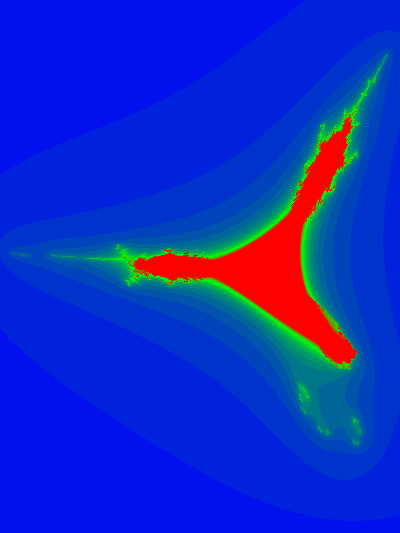
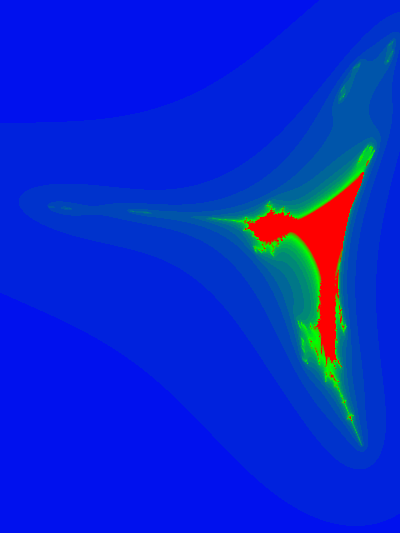
Here are some slice plots at various values of z

and an animation of the slices with respect to the z-axis:

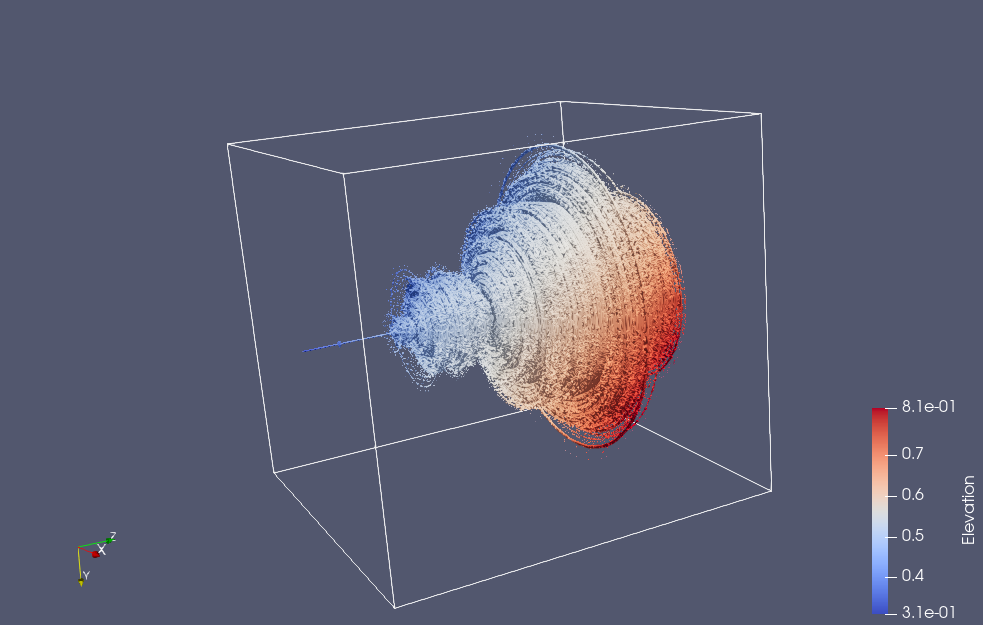
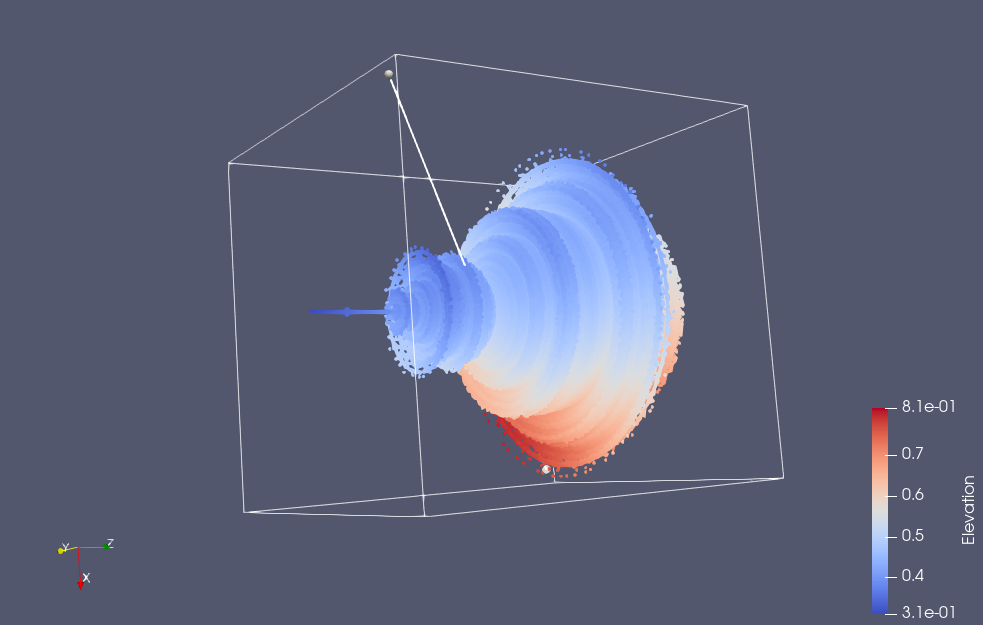
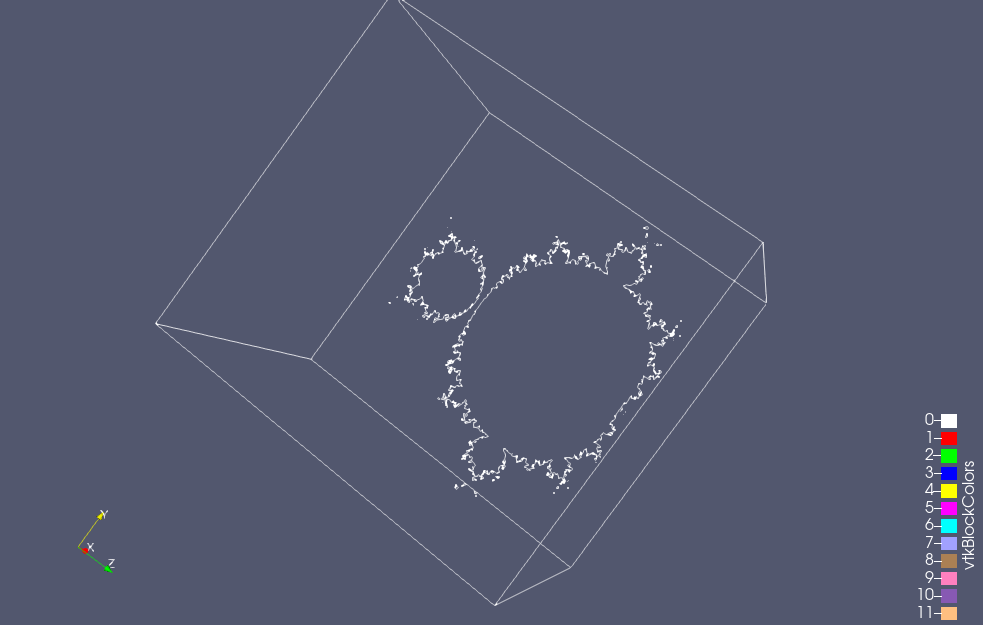
Here are a couple snapshots from a 3D Paraview rendering of a netCDF dataset of all the escape time values

Data collection and image creation used commit b042acf6ab7a5ba09865490b3f1fedaf0bd6e773 from my Mandelbrot generalization experimentation repository.

References

[1] L. Dorst, D. Fontijne, and S. Mann. Geometric Algebra for Computer Science. Morgan Kaufmann, San Francisco, 2007.

Some 3D renderings of the Mandelbrot set.

February 7, 2021 math and physics play , , , , ,

As mentioned previously, using geometric algebra we can convert the iterative equation for the Mandelbrot set from complex number form
\begin{equation}
z \rightarrow z^2 + c,
\end{equation}
to an equivalent vector form
\begin{equation}
\mathbf{x} \rightarrow \mathbf{x} \mathbf{e} \mathbf{x} + \mathbf{c},
\end{equation}
where \( \mathbf{e} \) represents the x-axis (say). Geometrically, each iteration takes \( \mathbf{e} \) and reflects it about the direction of \( \mathbf{x} \), then scales that by \( \mathbf{x}^2 \) and adds \( \mathbf{c} \).

To get the usual 2D Mandelbrot set, one iterates with vectors that lie only in the x-y plane, but we can treat the Mandelbrot set as a 3D solid if we remove the x-y plane restriction.

Last time I animated slices of the 3D set, but after a whole lot of messing around I managed to save the data for all the interior points of the 3D set in netCDF format, and render the solid using Paraview. Paraview has tons of filters available, and experimenting with them is pretty time consuming, but here are some initial screenshots of the 3D Mandelbrot set:

It’s interesting that much of the characteristic detail of the Mandelbrot set is not visible in the 3D volume, but if we slice that volume, you can then you can see it again.  Here’s a slice taken close to the z=0 plane (but far enough that the “CN tower” portion of the set is not visible)

You can also see some of that detail if the opacity of the rendering is turned way down:

If you look carefully at the images above, you’ll see that the axis labels are wrong.  I think that I’ve screwed up one of the stride related parameters to my putVar call, and I end up with x+z transposed in the axes labels when visualized.