[Click here for a PDF of this post with nicer formatting]
Disclaimer
Peeter’s lecture notes from class. These may be incoherent and rough.
Nonlinear differential equations
Assume that the relationships between the zeroth and first order derivatives has the form
\begin{equation}\label{eqn:multiphysicsL15:20}
F\lr{ x(t), \dot{x}(t) } = 0
\end{equation}
\begin{equation}\label{eqn:multiphysicsL15:40}
x(0) = x_0
\end{equation}
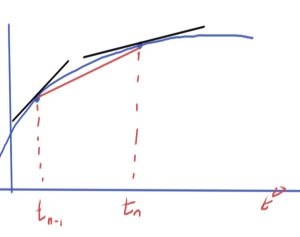
The backward Euler method where the derivative approximation is
\begin{equation}\label{eqn:multiphysicsL15:60}
\dot{x}(t_n) \approx \frac{x_n – x_{n-1}}{\Delta t},
\end{equation}
can be used to solve this numerically, reducing the problem to
\begin{equation}\label{eqn:multiphysicsL15:80}
F\lr{ x_n, \frac{x_n – x_{n-1}}{\Delta t} } = 0.
\end{equation}
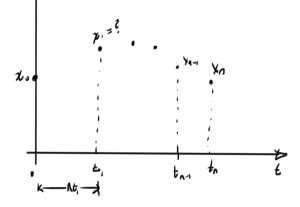
This can be solved with Newton’s method. How do we find the initial guess for Newton’s? Consider a possible system in fig. 1.
One strategy for starting each iteration of Newton’s method is to base the initial guess for \( x_1 \) on the value \( x_0 \), and do so iteratively for each subsequent point. One can imagine that this may work up to some sample point \( x_n \), but then break down (i.e. Newton’s diverges when the previous value \( x_{n-1} \) is used to attempt to solve for \( x_n \)). At that point other possible strategies may work. One such strategy is to use an approximation of the derivative from the previous steps to attempt to get a better estimate of the next value. Another possibility is to reduce the time step, so the difference between successive points is reduced.
Analysis, accuracy and stability (\(\Delta t \rightarrow 0\))
Consider a differential equation
\begin{equation}\label{eqn:multiphysicsL15:100}
\dot{x}(t) = f(x(t), t)
\end{equation}
\begin{equation}\label{eqn:multiphysicsL15:120}
x(t_0) = x_0
\end{equation}
A few methods of solution have been considered
- (FE) \( x_{n+1} – x_n = \Delta t f(x_n, t_n) \)
- (BE) \( x_{n+1} – x_n = \Delta t f(x_{n+1}, t_{n+1}) \)
- (TR) \( x_{n+1} – x_n = \frac{\Delta t}{2} f(x_{n+1}, t_{n+1}) + \frac{\Delta t}{2} f(x_{n}, t_{n}) \)
A common pattern can be observed, the generalization of which are called
\textit{linear multistep methods}
(LMS), which have the form
\begin{equation}\label{eqn:multiphysicsL15:140}
\sum_{j=-1}^{k-1} \alpha_j x_{n-j} = \Delta t \sum_{j=-1}^{k-1} \beta_j f( x_{n-j}, t_{n-j} )
\end{equation}
The FE (explicit), BE (implicit), and TR methods are now special cases with
- (FE) \( \alpha_{-1} = 1, \alpha_0 = -1, \beta_{-1} = 0, \beta_0 = 1 \)
- (BE) \( \alpha_{-1} = 1, \alpha_0 = -1, \beta_{-1} = 1, \beta_0 = 0 \)
- (TR) \( \alpha_{-1} = 1, \alpha_0 = -1, \beta_{-1} = 1/2, \beta_0 = 1/2 \)
Here \( k \) is the number of timesteps used. The method is explicit if \( \beta_{-1} = 0 \).
Definition: Convergence
With
- \(x(t)\) : exact solution
- \(x_n\) : computed solution
- \(e_n\) : where \( e_n = x_n – x(t_n) \), is the global error
The LMS method is convergent if
\begin{equation*}%\label{eqn:multiphysicsL15:180}
\max_{n, \Delta t \rightarrow 0} \Abs{ x_n – t(t_n) } \rightarrow 0 %\xrightarrow[t \rightarrow 0 ]{} 0
\end{equation*}
Convergence: zero-stability and consistency (small local errors made at each iteration),
where zero-stability is “small sensitivity to changes in initial condition”.
Definition: Consistency
A local error \( R_{n+1} \) can be defined as
\begin{equation*}%\label{eqn:multiphysicsL15:220}
R_{n+1} = \sum_{j = -1}^{k-1} \alpha_j x(t_{n-j}) – \Delta t \sum_{j=-1}^{k-1} \beta_j f(x(t_{n-j}), t_{n-j}).
\end{equation*}
The method is consistent if
\begin{equation*}%\label{eqn:multiphysicsL15:240}
\lim_{\Delta t} \lr{
\max_n \Abs{ \inv{\Delta t} R_{n+1} } = 0
}
\end{equation*}
or \( R_{n+1} \sim O({\Delta t}^2) \)