[Click here for a PDF version of this post]
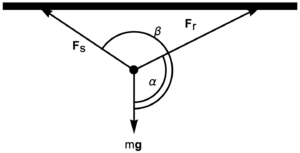
There’s a class of simple statics problems that are pervasive in high school physics and first year engineering classes (for me that CIV102.) These problems are illustrated in the figures below. Here we have a static load under gravity, and two supporting members (rigid beams or wire lines), which can be under compression, or tension, depending on the geometry.
The problem, given the geometry, is to find the magnitudes of the forces in the two members. The equation to solve is of the form
\begin{equation}\label{eqn:twoForceStaticsProblem:20}
\BF_s + \BF_r + m \Bg = 0.
\end{equation}
The usual way to solve such a problem is to resolve the forces into components. We will do that first here as a review, but then also solve the system using GA techniques, which are arguably simpler or more direct.
Solving as a conventional vector equation.
If we were back in high school we could have written our forces out in vector form
\begin{equation}\label{eqn:twoForceStaticsProblem:160}
\begin{aligned}
\BF_r &= f_r \lr{ \Be_1 \cos\alpha + \Be_2 \sin\alpha } \\
\BF_s &= f_s \lr{ \Be_1 \cos\beta + \Be_2 \sin\beta } \\
\Bg &= g \Be_1.
\end{aligned}
\end{equation}
Here the gravitational direction has been pointed along the x-axis.
Our equation to solve is now
\begin{equation}\label{eqn:twoForceStaticsProblem:180}
f_r \lr{ \Be_1 \cos\alpha + \Be_2 \sin\alpha } + f_s \lr{ \Be_1 \cos\beta + \Be_2 \sin\beta } + m g \Be_1 = 0.
\end{equation}
This we can solve as a set of scalar equations, one for each of the \( \Be_1 \) and \( \Be_2 \) directions
\begin{equation}\label{eqn:twoForceStaticsProblem:200}
\begin{aligned}
f_r \cos\alpha + f_s \cos\beta + m g &= 0 \\
f_r \sin\alpha + f_s \sin\beta &= 0.
\end{aligned}
\end{equation}
Our solution is
\begin{equation}\label{eqn:twoForceStaticsProblem:220}
\begin{aligned}
\begin{bmatrix}
f_r \\
f_s
\end{bmatrix}
&=
{\begin{bmatrix}
\cos\alpha & \cos\beta \\
\sin\alpha & \sin\beta
\end{bmatrix}}^{-1}
\begin{bmatrix}
– m g \\
0
\end{bmatrix} \\
&=
\inv{
\cos\alpha \sin\beta – \cos\beta \sin\alpha
}
\begin{bmatrix}
\sin\beta & -\cos\beta \\
-\sin\alpha & \cos\alpha
\end{bmatrix}
\begin{bmatrix}
– m g \\
0
\end{bmatrix} \\
&=
\frac{ m g }{ \cos\alpha \sin\beta – \cos\beta \sin\alpha }
\begin{bmatrix}
-\sin\beta \\
\sin\alpha
\end{bmatrix} \\
&=
\frac{ m g }{ \sin\lr{ \beta – \alpha } }
\begin{bmatrix}
-\sin\beta \\
\sin\alpha
\end{bmatrix}.
\end{aligned}
\end{equation}
We have to haul out some trig identities to make a final simplification, but find a solution to the system.
Another approach, is to take cross products with the unit force direction. First note that
\begin{equation}\label{eqn:twoForceStaticsProblem:240}
\begin{aligned}
\lr{ \Be_1 \cos\alpha + \Be_2 \sin\alpha } \cross \lr{ \Be_1 \cos\beta + \Be_2 \sin\beta }
&=
\Be_3 \lr{
\cos\alpha \sin\beta – \sin\alpha \cos\beta
} \\
&=
\Be_3 \sin\lr{ \beta – \alpha }.
\end{aligned}
\end{equation}
If we take cross products with each of the unit vectors, we find
\begin{equation}\label{eqn:twoForceStaticsProblem:260}
\begin{aligned}
f_r \lr{ \Be_1 \cos\alpha + \Be_2 \sin\alpha } \cross \lr{ \Be_1 \cos\beta + \Be_2 \sin\beta } + m g \Be_1 \cross \lr{ \Be_1 \cos\beta + \Be_2 \sin\beta } &= 0 \\
f_s \lr{ \Be_1 \cos\beta + \Be_2 \sin\beta } \cross \lr{ \Be_1 \cos\alpha + \Be_2 \sin\alpha } + m g \Be_1 \cross \lr{ \Be_1 \cos\alpha + \Be_2 \sin\alpha } &= 0,
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:twoForceStaticsProblem:280}
\begin{aligned}
\Be_3 f_r \sin\lr{ \beta – \alpha } + m g \Be_3 \sin\beta &= 0 \\
-\Be_3 f_s \sin\lr{ \beta – \alpha } + m g \Be_3 \sin\alpha &= 0.
\end{aligned}
\end{equation}
After cancelling the \( \Be_3 \)’s, we find the same result as we did solving the scalar system. This was a fairly direct way to solve the system, but the intermediate cross products were a bit messy. We will try this cross product using the wedge product. Switching from the cross to the wedge, by itself, will not make things any simpler or more complicated, but we can use the complex exponential form of the unit vectors for the forces, and that will make things simpler.
Geometric algebra setup and solution.
As usual for planar problems, let’s write \( i = \Be_1 \Be_2 \) for the plane pseudoscalar, which allows us to write the forces in polar form
\begin{equation}\label{eqn:twoForceStaticsProblem:40}
\begin{aligned}
\BF_r &= f_r \Be_1 e^{i\alpha} \\
\BF_s &= f_s \Be_1 e^{i\beta} \\
\Bg &= g \Be_1,
\end{aligned}
\end{equation}
Our equation to solve is now
\begin{equation}\label{eqn:twoForceStaticsProblem:60}
f_r \Be_1 e^{i\alpha} + f_s \Be_1 e^{i\beta} + m g \Be_1 = 0.
\end{equation}
The solution for either \( f_r \) or \( f_s \) is now trivial, as we only have to take wedge products with the force direction vectors to solve for the magnitudes. That is
\begin{equation}\label{eqn:twoForceStaticsProblem:80}
\begin{aligned}
f_r \lr{ \Be_1 e^{i\alpha} +} \wedge \lr{ \Be_1 e^{i\beta} } + m g \Be_1 \wedge \lr{ \Be_1 e^{i\beta} } &= 0 \\
f_s \lr{ \Be_1 e^{i\beta} +} \wedge \lr{ \Be_1 e^{i\alpha} } + m g \Be_1 \wedge \lr{ \Be_1 e^{i\alpha} } &= 0.
\end{aligned}
\end{equation}
Writing the wedges as grade two selections, and noting that \( e^{i\theta} \Be_1 = \Be_1 e^{-i\theta } \), we have
\begin{equation}\label{eqn:twoForceStaticsProblem:100}
\begin{aligned}
f_r &= – m g \frac{ \gpgradetwo{\Be_1^2 e^{i\beta}} }{ \gpgradetwo{ \Be_1^2 e^{-i\alpha} e^{i\beta} } } = – m g \frac{ \sin\beta }{ \sin\lr{ \beta – \alpha } } \\
f_s &= – m g \frac{ \gpgradetwo{\Be_1^2 e^{i\alpha}} }{ \gpgradetwo{ \Be_1^2 e^{-i\beta} e^{i\alpha} } } = m g \frac{ \sin\alpha }{ \sin\lr{ \beta – \alpha } }.
\end{aligned}
\end{equation}
The grade selection a unit pseudoscalar factor in both the denominator and numerator, which cancelled out to give the final scalar result.
As a complex variable problem.
Observe that we could have reframed the problem as a multivector problem by left multiplying \ref{eqn:twoForceStaticsProblem:60} by \( \Be_1 \) to find
\begin{equation}\label{eqn:twoForceStaticsProblem:120}
f_r e^{i\alpha} + f_s e^{i\beta} + m g = 0.
\end{equation}
Alternatively, we could have written the equations this way directly as a complex variable problem.
We can now solve for \( f_r \) or \( f_s \) by multiplying by the conjugate of one of the complex exponentials. That is
\begin{equation}\label{eqn:twoForceStaticsProblem:140}
\begin{aligned}
f_r + f_s e^{i\beta} e^{-i\alpha} + m g e^{-i\alpha} &= 0 \\
f_r e^{i\alpha} e^{-i\beta} + f_s + m g e^{-i\beta} &= 0.
\end{aligned}
\end{equation}
Selecting the bivector part of these equations (if interpreted as a multivector equation), or selecting the imaginary (if interpreting as a complex variables equation), will eliminate one of the force magnitudes from each equation, after which we find the same result.
This last approach, treating the problem as either a complex number problem (selecting imaginaries), or multivector problem (selecting bivectors), seems the simplest. We have no messing cross products, nor do we have to haul out the trig identities (the sine difference in the denominator comes practically for free, as it did with the wedge product method.)