Month: February 2017

ECE1505H Convex Optimization. Lecture 7: Examples of convex and concave functions, local and global minimums. Taught by Prof. Stark Draper

February 2, 2017 Uncategorized , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course ECE1505H, Convex Optimization, taught by Prof. Stark Draper, from [1].

Today

  • Local and global optimality
  • Compositions of functions
  • Examples

Example:

\begin{equation}\label{eqn:convexOptimizationLecture7:20}
\begin{aligned}
F(x) &= x^2 \\
F”(x) &= 2 > 0
\end{aligned}
\end{equation}

strictly convex.

Example:

\begin{equation}\label{eqn:convexOptimizationLecture7:40}
\begin{aligned}
F(x) &= x^3 \\
F”(x) &= 6 x.
\end{aligned}
\end{equation}

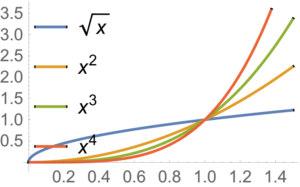
Not always non-negative, so not convex. However \( x^3 \) is convex on \( \textrm{dom} F = \mathbb{R}_{+} \).

Example:

\begin{equation}\label{eqn:convexOptimizationLecture7:60}
\begin{aligned}
F(x) &= x^\alpha \\
F'(x) &= \alpha x^{\alpha-1} \\
F”(x) &= \alpha(\alpha-1) x^{\alpha-2}.
\end{aligned}
\end{equation}

 

fig. 1. Powers of x.

This is convex on \( \mathbb{R}_{+} \), if \( \alpha \ge 1 \), or \( \alpha \le 0 \).

Example:

\begin{equation}\label{eqn:convexOptimizationLecture7:80}
\begin{aligned}
F(x) &= \log x \\
F'(x) &= \inv{x} \\
F”(x) &= -\inv{x^2} \le 0
\end{aligned}
\end{equation}

This is concave.

Example:

\begin{equation}\label{eqn:convexOptimizationLecture7:100}
\begin{aligned}
F(x) &= x\log x \\
F'(x) &= \log x + x \inv{x} = 1 + \log x \\
F”(x) &= \inv{x}
\end{aligned}
\end{equation}

This is strictly convex on
\( \mathbb{R}_{++} \), where
\( F”(x) \ge 0 \).

Example:

\begin{equation}\label{eqn:convexOptimizationLecture7:120}
\begin{aligned}
F(x) &= e^{\alpha x} \\
F'(x) &= \alpha e^{\alpha x} \\
F”(x) &= \alpha^2 e^{\alpha x} \ge 0
\end{aligned}
\end{equation}

fig. 2. Exponential.

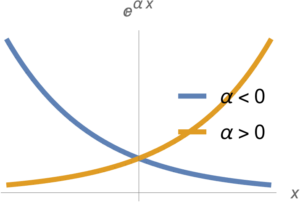
Such functions are plotted in fig. 2, and are convex function for all \( \alpha \).

Example:

For symmetric \( P \in S^n \)

\begin{equation}\label{eqn:convexOptimizationLecture7:140}
\begin{aligned}
F(\Bx) &= \Bx^\T P \Bx + 2 \Bq^\T \Bx + r \\
\spacegrad F &= (P + P^\T) \Bx + 2 \Bq = 2 P \Bx + 2 \Bq \\
\spacegrad^2 F &= 2 P.
\end{aligned}
\end{equation}

This is convex(concave) if \( P \ge 0 \) (\( P \le 0\)).

Example:

A quadratic function

\begin{equation}\label{eqn:convexOptimizationLecture7:780}
F(x, y) = x^2 + y^2 + 3 x y,
\end{equation}

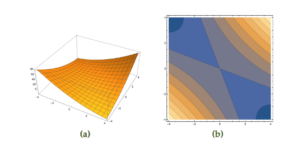
that is neither convex nor concave is plotted in fig 3.

fig 3. Function with saddle point (3d and contours)

This function can be put in matrix form

\begin{equation}\label{eqn:convexOptimizationLecture7:160}
F(x, y) = x^2 + y^2 + 3 x y
=
\begin{bmatrix}
x & y
\end{bmatrix}
\begin{bmatrix}
1 & 1.5 \\
1.5 & 1
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix},
\end{equation}

and has the Hessian

\begin{equation}\label{eqn:convexOptimizationLecture7:180}
\begin{aligned}
\spacegrad^2 F
&=
\begin{bmatrix}
\partial_{xx} F & \partial_{xy} F \\
\partial_{yx} F & \partial_{yy} F \\
\end{bmatrix} \\
&=
\begin{bmatrix}
2 & 3 \\
3 & 2
\end{bmatrix} \\
&= 2 P.
\end{aligned}
\end{equation}

From the plot we know that this is not PSD, but this can be confirmed by checking the eigenvalues

\begin{equation}\label{eqn:convexOptimizationLecture7:200}
\begin{aligned}
0
&=
\det ( P – \lambda I ) \\
&=
(1 – \lambda)^2 – 1.5^2,
\end{aligned}
\end{equation}

which has solutions

\begin{equation}\label{eqn:convexOptimizationLecture7:220}
\lambda = 1 \pm \frac{3}{2} = \frac{3}{2}, -\frac{1}{2}.
\end{equation}

This is not PSD nor negative semi-definite, because it has one positive and one negative eigenvalues. This is neither convex nor concave.

Along \( y = -x \),

\begin{equation}\label{eqn:convexOptimizationLecture7:240}
\begin{aligned}
F(x,y)
&=
F(x,-x) \\
&=
2 x^2 – 3 x^2 \\
&=
– x^2,
\end{aligned}
\end{equation}

so it is concave along this line. Along \( y = x \)

\begin{equation}\label{eqn:convexOptimizationLecture7:260}
\begin{aligned}
F(x,y)
&=
F(x,x) \\
&=
2 x^2 + 3 x^2 \\
&=
5 x^2,
\end{aligned}
\end{equation}

so it is convex along this line.

Example:

\begin{equation}\label{eqn:convexOptimizationLecture7:280}
F(\Bx) = \sqrt{ x_1 x_2 },
\end{equation}

on \( \textrm{dom} F = \setlr{ x_1 \ge 0, x_2 \ge 0 } \)

For the Hessian
\begin{equation}\label{eqn:convexOptimizationLecture7:300}
\begin{aligned}
\PD{x_1}{F} &= \frac{1}{2} x_1^{-1/2} x_2^{1/2} \\
\PD{x_2}{F} &= \frac{1}{2} x_2^{-1/2} x_1^{1/2}
\end{aligned}
\end{equation}

The Hessian components are

\begin{equation}\label{eqn:convexOptimizationLecture7:320}
\begin{aligned}
\PD{x_1}{} \PD{x_1}{F} &= -\frac{1}{4} x_1^{-3/2} x_2^{1/2} \\
\PD{x_1}{} \PD{x_2}{F} &= \frac{1}{4} x_2^{-1/2} x_1^{-1/2} \\
\PD{x_2}{} \PD{x_1}{F} &= \frac{1}{4} x_1^{-1/2} x_2^{-1/2} \\
\PD{x_2}{} \PD{x_2}{F} &= -\frac{1}{4} x_2^{-3/2} x_1^{1/2}
\end{aligned}
\end{equation}

or
\begin{equation}\label{eqn:convexOptimizationLecture7:340}
\spacegrad^2 F
=
-\frac{\sqrt{x_1 x_2}}{4}
\begin{bmatrix}
\inv{x_1^2} & -\inv{x_1 x_2} \\
-\inv{x_1 x_2} & \inv{x_2^2}
\end{bmatrix}.
\end{equation}

Checking this for PSD against \( \Bv = (v_1, v_2) \), we have
\begin{equation}\label{eqn:convexOptimizationLecture7:360}
\begin{aligned}
\begin{bmatrix}
v_1 & v_2
\end{bmatrix}
\begin{bmatrix}
\inv{x_1^2} & -\inv{x_1 x_2} \\
-\inv{x_1 x_2} & \inv{x_2^2}
\end{bmatrix}
\begin{bmatrix}
v_1 \\ v_2
\end{bmatrix}
&=
\begin{bmatrix}
v_1 & v_2
\end{bmatrix}
\begin{bmatrix}
\inv{x_1^2} v_1 -\inv{x_1 x_2} v_2 \\
-\inv{x_1 x_2} v_1 + \inv{x_2^2} v_2
\end{bmatrix} \\
&=
\lr{ \inv{x_1^2} v_1 -\inv{x_1 x_2} v_2 } v_1 +
\lr{ -\inv{x_1 x_2} v_1 + \inv{x_2^2} v_2 } v_2
\\
&=
\inv{x_1^2} v_1^2
+ \inv{x_2^2} v_2^2
-2 \inv{x_1 x_2} v_1 v_2 \\
&=
\lr{
\frac{v_1}{x_1}
-\frac{v_2}{x_2}
}^2 \\
&\ge 0,
\end{aligned}
\end{equation}

so \( \spacegrad^2 F \le 0 \). This is a negative semi-definite function (concave). Observe that this check required checking PSD for all values of \( \Bx \).

This is an example of a more general result

\begin{equation}\label{eqn:convexOptimizationLecture7:380}
F(x) = \lr{ \prod_{i = 1}^n x_i }^{1/n},
\end{equation}

which is concave (prove on homework).

Summary.

If \( F \) is differentiable in \R{n}, then check the curvature of the function along all lines. i.e. At all locations and in all directions.

If the Hessian is PSD at all \( \Bx \in \textrm{dom} F \), that is

\begin{equation}\label{eqn:convexOptimizationLecture7:400}
\spacegrad^2 F \ge 0 \, \forall \Bx \in \textrm{dom} F,
\end{equation}

then the function is convex.

more examples of convex, but not necessarily differentiable functions

Example:

Over \( \textrm{dom} F = \mathbb{R}^n \)

\begin{equation}\label{eqn:convexOptimizationLecture7:420}
F(\Bx) = \max_{i = 1}^n x_i
\end{equation}

i.e.
\begin{equation}\label{eqn:convexOptimizationLecture7:440}
\begin{aligned}
F((1,2) &= 2 \\
F((3,-1) &= 3
\end{aligned}
\end{equation}

Example:

\begin{equation}\label{eqn:convexOptimizationLecture7:460}
F(\Bx) = \max_{i = 1}^n F_i(\Bx),
\end{equation}

where

\begin{equation}\label{eqn:convexOptimizationLecture7:480}
F_i(\Bx)
=
… ?
\end{equation}

max of a set of convex functions is a convex function.

Example:

\begin{equation}\label{eqn:convexOptimizationLecture7:500}
F(x) =
x_{[1]} +
x_{[2]} +
x_{[3]}
\end{equation}

where

\( x_{[k]} \) is the k-th largest number in the list

Write

\begin{equation}\label{eqn:convexOptimizationLecture7:520}
F(x) = \max x_i + x_j + x_k
\end{equation}

\begin{equation}\label{eqn:convexOptimizationLecture7:540}
(i,j,k) \in \binom{n}{3}
\end{equation}

Example:

For \( \Ba \in \mathbb{R}^n \) and \( b_i \in \mathbb{R} \)

\begin{equation}\label{eqn:convexOptimizationLecture7:560}
\begin{aligned}
F(\Bx)
&= \sum_{i = 1}^n \log( b_i – \Ba^\T \Bx )^{-1} \\
&= -\sum_{i = 1}^n \log( b_i – \Ba^\T \Bx )
\end{aligned}
\end{equation}

This \( b_i – \Ba^\T \Bx \) is an affine function of \( \Bx \) so it doesn’t affect convexity.

Since \( \log \) is concave, \( -\log \) is convex. Convex functions of affine function of \( \Bx \) is convex function of \( \Bx \).

Example:

\begin{equation}\label{eqn:convexOptimizationLecture7:580}
F(\Bx) = \sup_{\By \in C} \Norm{ \Bx – \By }
\end{equation}

 

fig. 3. Max length function

 

Here \( C \subseteq \mathbb{R}^n \) is not necessarily convex. We are using \( \sup \) here because the set \( C \) may be open. This function is the length of the line from \( \Bx \) to the point in \( C \) that is furthest from \( \Bx \).

  • \( \Bx – \By \) is linear in \( \Bx \)
  • \( g_\By(\Bx) = \Norm{\Bx – \By} \) is convex in \( \Bx \) since norms are convex functions.
  • \( F(\Bx) = \sup_{\By \in C} \Norm{ \Bx – \By } \). Each \( \By \) index is a convex function. Taking max of those.

Example:

\begin{equation}\label{eqn:convexOptimizationLecture7:600}
F(\Bx) = \inf_{\By \in C} \Norm{ \Bx – \By }.
\end{equation}

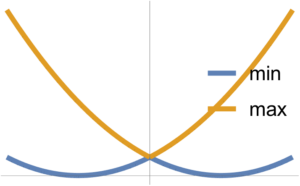
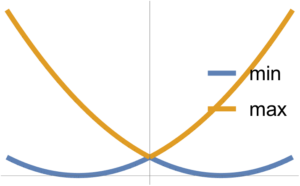
Min and max of two convex functions are plotted in fig. 4.

fig. 4. Min and max

The max is observed to be convex, whereas the min is not necessarily so.

\begin{equation}\label{eqn:convexOptimizationLecture7:800}
F(\Bz) = F(\theta \Bx + (1-\theta) \By) \ge \theta F(\Bx) + (1-\theta)F(\By).
\end{equation}

This is not necessarily convex for all sets \( C \subseteq \mathbb{R}^n \), because the \( \inf \) of a bunch of convex function is not necessarily convex. However, if \( C \) is convex, then \( F(\Bx) \) is convex.

Consequences of convexity for differentiable functions

  • Think about unconstrained functions \( \textrm{dom} F = \mathbb{R}^n \).
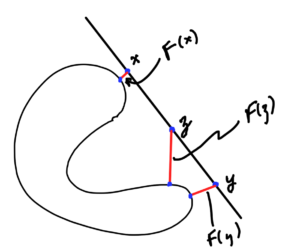
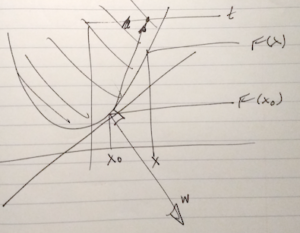
  • By first order condition \( F \) is convex iff the domain is convex and
    \begin{equation}\label{eqn:convexOptimizationLecture7:620}
    F(\Bx) \ge \lr{ \spacegrad F(\Bx)}^\T (\By – \Bx) \, \forall \Bx, \By \in \textrm{dom} F.
    \end{equation}

If \( F \) is convex and one can find an \( \Bx^\conj \in \textrm{dom} F \) such that

\begin{equation}\label{eqn:convexOptimizationLecture7:640}
\spacegrad F(\Bx^\conj) = 0,
\end{equation}

then

\begin{equation}\label{eqn:convexOptimizationLecture7:660}
F(\By) \ge F(\Bx^\conj) \, \forall \By \in \textrm{dom} F.
\end{equation}

If you can find the point where the gradient is zero (which can’t always be found), then \( \Bx^\conj\) is a global minimum of \( F \).

Conversely, if \( \Bx^\conj \) is a global minimizer of \( F \), then \( \spacegrad F(\Bx^\conj) = 0 \) must hold. If that were not the case, then you would be able to find a direction to move downhill, contracting the optimality of \( \Bx^\conj\).

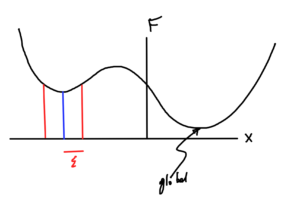
Local vs Global optimum

 

fig. 6. Global and local minimums

Definition: Local optimum
\( \Bx^\conj \) is a local optimum of \( F \) if \( \exists \epsilon > 0 \) such that \( \forall \Bx \), \( \Norm{\Bx – \Bx^\conj} < \epsilon \), we have

\begin{equation*}
F(\Bx^\conj) \le F(\Bx)
\end{equation*}

 

fig. 5. min length function

Theorem:
Suppose \( F \) is twice continuously differentiable (not necessarily convex)

  • If \( \Bx^\conj\) is a local optimum then\begin{equation*}
    \begin{aligned}
    \spacegrad F(\Bx^\conj) &= 0 \\
    \spacegrad^2 F(\Bx^\conj) \ge 0
    \end{aligned}
    \end{equation*}
  • If
    \begin{equation*}
    \begin{aligned}
    \spacegrad F(\Bx^\conj) &= 0 \\
    \spacegrad^2 F(\Bx^\conj) \ge 0
    \end{aligned},
    \end{equation*}then \( \Bx^\conj\) is a local optimum.

Proof:

  • Let \( \Bx^\conj \) be a local optimum. Pick any \( \Bv \in \mathbb{R}^n \).\begin{equation}\label{eqn:convexOptimizationLecture7:720}
    \lim_{t \rightarrow 0} \frac{ F(\Bx^\conj + t \Bv) – F(\Bx^\conj)}{t}
    = \lr{ \spacegrad F(\Bx^\conj) }^\T \Bv
    \ge 0.
    \end{equation}

Here the fraction is \( \ge 0 \) since \( \Bx^\conj \) is a local optimum.

Since the choice of \( \Bv \) is arbitrary, the only case that you can ensure that \( \ge 0, \forall \Bv \) is

\begin{equation}\label{eqn:convexOptimizationLecture7:740}
\spacegrad F = 0,
\end{equation}

( or else could pick \( \Bv = -\spacegrad F(\Bx^\conj) \).

This means that \( \spacegrad F(\Bx^\conj) = 0 \) if \( \Bx^\conj \) is a local optimum.

Consider the 2nd order derivative

\begin{equation}\label{eqn:convexOptimizationLecture7:760}
\begin{aligned}
\lim_{t \rightarrow 0} \frac{ F(\Bx^\conj + t \Bv) – F(\Bx^\conj)}{t^2}
&=
\lim_{t \rightarrow 0} \inv{t^2}
\lr{
F(\Bx^\conj) + t \lr{ \spacegrad F(\Bx^\conj) }^\T \Bv + \inv{2} t^2 \Bv^\T \spacegrad^2 F(\Bx^\conj) \Bv + O(t^3)
– F(\Bx^\conj)
} \\
&=
\inv{2} \Bv^\T \spacegrad^2 F(\Bx^\conj) \Bv \\
&\ge 0.
\end{aligned}
\end{equation}

Here the \( \ge \) condition also comes from the fraction, based on the optimiality of \( \Bx^\conj \). This is true for all choice of \( \Bv \), thus \( \spacegrad^2 F(\Bx^\conj) \).

References

[1] Stephen Boyd and Lieven Vandenberghe. Convex optimization. Cambridge university press, 2004.

ECE1505H Convex Optimization. Lecture 6: First and second order conditions. Taught by Prof.\ Stark Draper

February 1, 2017 ece1505 , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course ECE1505H, Convex Optimization, taught by Prof. Stark Draper, from [1].

Today

  • First and second order conditions for convexity of differentiable functions.
  • Consequences of convexity: local and global optimality.
  • Properties.

Quasi-convex

\( F_1 \) and \( F_2 \) convex implies \( \max( F_1, F_2) \) convex.

 

fig. 1. Min and Max

Note that \( \min(F_1, F_2) \) is NOT convex.

If \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) is convex, then \( F( \Bx_0 + t \Bv ) \) is convex in \( t\,\forall t \in \mathbb{R}, \Bx_0 \in \mathbb{R}^n, \Bv \in \mathbb{R}^n \), provided \( \Bx_0 + t \Bv \in \textrm{dom} F \).

Idea: Restrict to a line (line segment) in \( \textrm{dom} F \). Take a cross section or slice through \( F \) alone the line. If the result is a 1D convex function for all slices, then \( F \) is convex.

This is nice since it allows for checking for convexity, and is also nice numerically. Attempting to test a given data set for non-convexity with some random lines can help disprove convexity. However, to show that \( F \) is convex it is required to test all possible slices (which isn’t possible numerically, but is in some circumstances possible analytically).

Differentiable (convex) functions

Definition: First order condition.

If

\begin{equation*}
F : \mathbb{R}^n \rightarrow \mathbb{R}
\end{equation*}

is differentiable, then \( F \) is convex iff \( \textrm{dom} F \) is a convex set and \( \forall \Bx, \Bx_0 \in \textrm{dom} F \)

\begin{equation*}
F(\Bx) \ge F(\Bx_0) + \lr{\spacegrad F(\Bx_0)}^\T (\Bx – \Bx_0).
\end{equation*}

This is the first order Taylor expansion. If \( n = 1 \), this is \( F(x) \ge F(x_0) + F'(x_0) ( x – x_0) \).

The first order condition says a convex function \underline{always} lies above its first order approximation, as sketched in fig. 3.

 

fig. 2. First order approximation lies below convex function

When differentiable, the supporting plane is the tangent plane.

Definition: Second order condition

If \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) is twice differentiable, then \( F \) is convex iff \( \textrm{dom} F \) is a convex set and \( \spacegrad^2 F(\Bx) \ge 0 \,\forall \Bx \in \textrm{dom} F\).

The Hessian is always symmetric, but is not necessarily positive. Recall that the Hessian is the matrix of the second order partials \( (\spacegrad F)_{ij} = \partial^2 F/(\partial x_i \partial x_j) \).

The scalar case is \( F”(x) \ge 0 \, \forall x \in \textrm{dom} F \).

An implication is that if \( F \) is convex, then \( F(x) \ge F(x_0) + F'(x_0) (x – x_0) \,\forall x, x_0 \in \textrm{dom} F\)

Since \( F \) is convex, \( \textrm{dom} F \) is convex.

Consider any 2 points \( x, y \in \textrm{dom} F \), and \( \theta \in [0,1] \). Define

\begin{equation}\label{eqn:convexOptimizationLecture6:60}
z = (1-\theta) x + \theta y \in \textrm{dom} F,
\end{equation}

then since \( \textrm{dom} F \) is convex

\begin{equation}\label{eqn:convexOptimizationLecture6:80}
F(z) =
F( (1-\theta) x + \theta y )
\le
(1-\theta) F(x) + \theta F(y )
\end{equation}

Reordering

\begin{equation}\label{eqn:convexOptimizationLecture6:220}
\theta F(x) \ge
\theta F(x) + F(z) – F(x),
\end{equation}

or
\begin{equation}\label{eqn:convexOptimizationLecture6:100}
F(y) \ge
F(x) + \frac{F(x + \theta(y-x)) – F(x)}{\theta},
\end{equation}

which is, in the limit,

\begin{equation}\label{eqn:convexOptimizationLecture6:120}
F(y) \ge
F(x) + F'(x) (y – x),
\end{equation}

completing one direction of the proof.

To prove the other direction, showing that

\begin{equation}\label{eqn:convexOptimizationLecture6:140}
F(x) \ge F(x_0) + F'(x_0) (x – x_0),
\end{equation}

implies that \( F \) is convex. Take any \( x, y \in \textrm{dom} F \) and any \( \theta \in [0,1] \). Define

\begin{equation}\label{eqn:convexOptimizationLecture6:160}
z = \theta x + (1 -\theta) y,
\end{equation}

which is in \( \textrm{dom} F \) by assumption. We want to show that

\begin{equation}\label{eqn:convexOptimizationLecture6:180}
F(z) \le \theta F(x) + (1-\theta) F(y).
\end{equation}

By assumption

  1. \( F(x) \ge F(z) + F'(z) (x – z) \)
  2. \( F(y) \ge F(z) + F'(z) (y – z) \)

Compute

\begin{equation}\label{eqn:convexOptimizationLecture6:200}
\begin{aligned}
\theta F(x) + (1-\theta) F(y)
&\ge
\theta \lr{ F(z) + F'(z) (x – z) }
+ (1-\theta) \lr{ F(z) + F'(z) (y – z) } \\
&=
F(z) + F'(z) \lr{ \theta( x – z) + (1-\theta) (y-z) } \\
&=
F(z) + F'(z) \lr{ \theta x + (1-\theta) y – \theta z – (1 -\theta) z } \\
&=
F(z) + F'(z) \lr{ \theta x + (1-\theta) y – z} \\
&=
F(z) + F'(z) \lr{ z – z} \\
&= F(z).
\end{aligned}
\end{equation}

Proof of the 2nd order case for \( n = 1 \)

Want to prove that if

\begin{equation}\label{eqn:convexOptimizationLecture6:240}
F : \mathbb{R} \rightarrow \mathbb{R}
\end{equation}

is a convex function, then \( F”(x) \ge 0 \,\forall x \in \textrm{dom} F \).

By the first order conditions \( \forall x \ne y \in \textrm{dom} F \)

\begin{equation}\label{eqn:convexOptimizationLecture6:260}
\begin{aligned}
F(y) &\ge F(x) + F'(x) (y – x)
F(x) &\ge F(y) + F'(y) (x – y)
\end{aligned}
\end{equation}

Can combine and get

\begin{equation}\label{eqn:convexOptimizationLecture6:280}
F'(x) (y-x) \le F(y) – F(x) \le F'(y)(y-x)
\end{equation}

Subtract the two derivative terms for

\begin{equation}\label{eqn:convexOptimizationLecture6:340}
\frac{(F'(y) – F'(x))(y – x)}{(y – x)^2} \ge 0,
\end{equation}

or
\begin{equation}\label{eqn:convexOptimizationLecture6:300}
\frac{F'(y) – F'(x)}{y – x} \ge 0.
\end{equation}

In the limit as \( y \rightarrow x \), this is
\begin{equation}\label{eqn:convexOptimizationLecture6:320}
\boxed{
F”(x) \ge 0 \,\forall x \in \textrm{dom} F.
}
\end{equation}

Now prove the reverse condition:

If \( F”(x) \ge 0 \,\forall x \in \textrm{dom} F \subseteq \mathbb{R} \), implies that \( F : \mathbb{R} \rightarrow \mathbb{R} \) is convex.

Note that if \( F”(x) \ge 0 \), then \( F'(x) \) is non-decreasing in \( x \).

i.e. If \( x < y \), where \( x, y \in \textrm{dom} F\), then

\begin{equation}\label{eqn:convexOptimizationLecture6:360}
F'(x) \le F'(y).
\end{equation}

Consider any \( x,y \in \textrm{dom} F\) such that \( x < y \), where

\begin{equation}\label{eqn:convexOptimizationLecture6:380}
F(y) – F(x) = \int_x^y F'(t) dt \ge F'(x) \int_x^y 1 dt = F'(x) (y-x).
\end{equation}

This tells us that

\begin{equation}\label{eqn:convexOptimizationLecture6:400}
F(y) \ge F(x) + F'(x)(y – x),
\end{equation}

which is the first order condition. Similarly consider any \( x,y \in \textrm{dom} F\) such that \( x < y \), where

\begin{equation}\label{eqn:convexOptimizationLecture6:420}
F(y) – F(x) = \int_x^y F'(t) dt \le F'(y) \int_x^y 1 dt = F'(y) (y-x).
\end{equation}

This tells us that

\begin{equation}\label{eqn:convexOptimizationLecture6:440}
F(x) \ge F(y) + F'(y)(x – y).
\end{equation}

Vector proof:

\( F \) is convex iff \( F(\Bx + t \Bv) \) is convex \( \forall \Bx,\Bv \in \mathbb{R}^n, t \in \mathbb{R} \), keeping \( \Bx + t \Bv \in \textrm{dom} F\).

Let
\begin{equation}\label{eqn:convexOptimizationLecture6:460}
h(t ; \Bx, \Bv) = F(\Bx + t \Bv)
\end{equation}

then \( h(t) \) satisfies scalar first and second order conditions for all \( \Bx, \Bv \).

\begin{equation}\label{eqn:convexOptimizationLecture6:480}
h(t) = F(\Bx + t \Bv) = F(g(t)),
\end{equation}

where \( g(t) = \Bx + t \Bv \), where

\begin{equation}\label{eqn:convexOptimizationLecture6:500}
\begin{aligned}
F &: \mathbb{R}^n \rightarrow \mathbb{R} \\
g &: \mathbb{R} \rightarrow \mathbb{R}^n.
\end{aligned}
\end{equation}

This is expressing \( h(t) \) as a composition of two functions. By the first order condition for scalar functions we know that

\begin{equation}\label{eqn:convexOptimizationLecture6:520}
h(t) \ge h(0) + h'(0) t.
\end{equation}

Note that

\begin{equation}\label{eqn:convexOptimizationLecture6:540}
h(0) = \evalbar{F(\Bx + t \Bv)}{t = 0} = F(\Bx).
\end{equation}

Let’s figure out what \( h'(0) \) is. Recall hat for any \( \tilde{F} : \mathbb{R}^n \rightarrow \mathbb{R}^m \)

\begin{equation}\label{eqn:convexOptimizationLecture6:560}
D \tilde{F} \in \mathbb{R}^{m \times n},
\end{equation}

and
\begin{equation}\label{eqn:convexOptimizationLecture6:580}
{D \tilde{F}(\Bx)}_{ij} = \PD{x_j}{\tilde{F_i}(\Bx)}
\end{equation}

This is one function per row, for \( i \in [1,m], j \in [1,n] \). This gives

\begin{equation}\label{eqn:convexOptimizationLecture6:600}
\begin{aligned}
\frac{d}{dt} F(\Bx + \Bv t)
&=
\frac{d}{dt} F( g(t) ) \\
&=
\frac{d}{dt} h(t) \\
&= D h(t) \\
&= D F(g(t)) \cdot D g(t)
\end{aligned}
\end{equation}

The first matrix is in \( \mathbb{R}^{1\times n} \) whereas the second is in \( \mathbb{R}^{n\times 1} \), since \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) and \( g : \mathbb{R} \rightarrow \mathbb{R}^n \). This gives

\begin{equation}\label{eqn:convexOptimizationLecture6:620}
\frac{d}{dt} F(\Bx + \Bv t)
= \evalbar{D F(\tilde{\Bx})}{\tilde{\Bx} = g(t)} \cdot D g(t).
\end{equation}

That first matrix is

\begin{equation}\label{eqn:convexOptimizationLecture6:640}
\begin{aligned}
\evalbar{D F(\tilde{\Bx})}{\tilde{\Bx} = g(t)}
&=
\evalbar{
\lr{\begin{bmatrix}
\PD{\tilde{x}_1}{ F(\tilde{\Bx})} &
\PD{\tilde{x}_2}{ F(\tilde{\Bx})} & \cdots
\PD{\tilde{x}_n}{ F(\tilde{\Bx})}
\end{bmatrix}
}}{ \tilde{\Bx} = g(t) = \Bx + t \Bv } \\
&=
\evalbar{
\lr{ \spacegrad F(\tilde{\Bx}) }^\T
}{
\tilde{\Bx} = g(t)
} \\
=
\lr{ \spacegrad F(g(t)) }^\T.
\end{aligned}
\end{equation}

The second Jacobian is

\begin{equation}\label{eqn:convexOptimizationLecture6:660}
D g(t)
=
D
\begin{bmatrix}
g_1(t) \\
g_2(t) \\
\vdots \\
g_n(t) \\
\end{bmatrix}
=
D
\begin{bmatrix}
x_1 + t v_1 \\
x_2 + t v_2 \\
\vdots \\
x_n + t v_n \\
\end{bmatrix}
=
\begin{bmatrix}
v_1 \\
v_1 \\
\vdots \\
v_n \\
\end{bmatrix}
=
\Bv.
\end{equation}

so

\begin{equation}\label{eqn:convexOptimizationLecture6:680}
h'(t) = D h(t) = \lr{ \spacegrad F(g(t))}^\T \Bv,
\end{equation}

and
\begin{equation}\label{eqn:convexOptimizationLecture6:700}
h'(0) = \lr{ \spacegrad F(g(0))}^\T \Bv
=
\lr{ \spacegrad F(\Bx)}^\T \Bv.
\end{equation}

Finally

\begin{equation}\label{eqn:convexOptimizationLecture6:720}
\begin{aligned}
F(\Bx + t \Bv)
&\ge h(0) + h'(0) t \\
&= F(\Bx) + \lr{ \spacegrad F(\Bx) }^\T (t \Bv) \\
&= F(\Bx) + \innerprod{ \spacegrad F(\Bx) }{ t \Bv}.
\end{aligned}
\end{equation}

Which is true for all \( \Bx, \Bx + t \Bv \in \textrm{dom} F \). Note that the quantity \( t \Bv \) is a shift.

Epigraph

Recall that if \( (\Bx, t) \in \textrm{epi} F \) then \( t \ge F(\Bx) \).

\begin{equation}\label{eqn:convexOptimizationLecture6:740}
t \ge F(\Bx) \ge F(\Bx_0) + \lr{\spacegrad F(\Bx_0) }^\T (\Bx – \Bx_0),
\end{equation}

or

\begin{equation}\label{eqn:convexOptimizationLecture6:760}
0 \ge
-(t – F(\Bx_0)) + \lr{\spacegrad F(\Bx_0) }^\T (\Bx – \Bx_0),
\end{equation}

In block matrix form

\begin{equation}\label{eqn:convexOptimizationLecture6:780}
0 \ge
\begin{bmatrix}
\lr{ \spacegrad F(\Bx_0) }^\T & -1
\end{bmatrix}
\begin{bmatrix}
\Bx – \Bx_0 \\
t – F(\Bx_0)
\end{bmatrix}
\end{equation}

With \( \Bw =
\begin{bmatrix}
\lr{ \spacegrad F(\Bx_0) }^\T & -1
\end{bmatrix} \), the geometry of the epigraph relation to the half plane is sketched in fig. 3.

 

fig. 3. Half planes and epigraph.

References

[1] Stephen Boyd and Lieven Vandenberghe. Convex optimization. Cambridge university press, 2004.