[Click here for a PDF of this post with nicer formatting]
Disclaimer
Peeter’s lecture notes from class. These may be incoherent and rough.
These are notes for the UofT course ECE1505H, Convex Optimization, taught by Prof. Stark Draper, from [1].
Today
- First and second order conditions for convexity of differentiable functions.
- Consequences of convexity: local and global optimality.
- Properties.
Quasi-convex
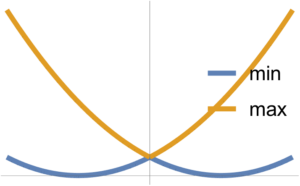
\( F_1 \) and \( F_2 \) convex implies \( \max( F_1, F_2) \) convex.
Note that \( \min(F_1, F_2) \) is NOT convex.
If \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) is convex, then \( F( \Bx_0 + t \Bv ) \) is convex in \( t\,\forall t \in \mathbb{R}, \Bx_0 \in \mathbb{R}^n, \Bv \in \mathbb{R}^n \), provided \( \Bx_0 + t \Bv \in \textrm{dom} F \).
Idea: Restrict to a line (line segment) in \( \textrm{dom} F \). Take a cross section or slice through \( F \) alone the line. If the result is a 1D convex function for all slices, then \( F \) is convex.
This is nice since it allows for checking for convexity, and is also nice numerically. Attempting to test a given data set for non-convexity with some random lines can help disprove convexity. However, to show that \( F \) is convex it is required to test all possible slices (which isn’t possible numerically, but is in some circumstances possible analytically).
Differentiable (convex) functions
Definition: First order condition.
If
\begin{equation*}
F : \mathbb{R}^n \rightarrow \mathbb{R}
\end{equation*}
is differentiable, then \( F \) is convex iff \( \textrm{dom} F \) is a convex set and \( \forall \Bx, \Bx_0 \in \textrm{dom} F \)
\begin{equation*}
F(\Bx) \ge F(\Bx_0) + \lr{\spacegrad F(\Bx_0)}^\T (\Bx – \Bx_0).
\end{equation*}
This is the first order Taylor expansion. If \( n = 1 \), this is \( F(x) \ge F(x_0) + F'(x_0) ( x – x_0) \).
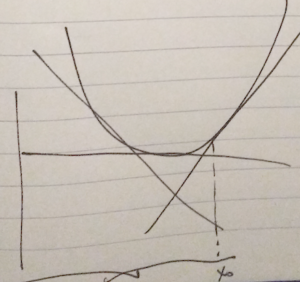
The first order condition says a convex function \underline{always} lies above its first order approximation, as sketched in fig. 3.
When differentiable, the supporting plane is the tangent plane.
Definition: Second order condition
If \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) is twice differentiable, then \( F \) is convex iff \( \textrm{dom} F \) is a convex set and \( \spacegrad^2 F(\Bx) \ge 0 \,\forall \Bx \in \textrm{dom} F\).
The Hessian is always symmetric, but is not necessarily positive. Recall that the Hessian is the matrix of the second order partials \( (\spacegrad F)_{ij} = \partial^2 F/(\partial x_i \partial x_j) \).
The scalar case is \( F”(x) \ge 0 \, \forall x \in \textrm{dom} F \).
An implication is that if \( F \) is convex, then \( F(x) \ge F(x_0) + F'(x_0) (x – x_0) \,\forall x, x_0 \in \textrm{dom} F\)
Since \( F \) is convex, \( \textrm{dom} F \) is convex.
Consider any 2 points \( x, y \in \textrm{dom} F \), and \( \theta \in [0,1] \). Define
\begin{equation}\label{eqn:convexOptimizationLecture6:60}
z = (1-\theta) x + \theta y \in \textrm{dom} F,
\end{equation}
then since \( \textrm{dom} F \) is convex
\begin{equation}\label{eqn:convexOptimizationLecture6:80}
F(z) =
F( (1-\theta) x + \theta y )
\le
(1-\theta) F(x) + \theta F(y )
\end{equation}
Reordering
\begin{equation}\label{eqn:convexOptimizationLecture6:220}
\theta F(x) \ge
\theta F(x) + F(z) – F(x),
\end{equation}
or
\begin{equation}\label{eqn:convexOptimizationLecture6:100}
F(y) \ge
F(x) + \frac{F(x + \theta(y-x)) – F(x)}{\theta},
\end{equation}
which is, in the limit,
\begin{equation}\label{eqn:convexOptimizationLecture6:120}
F(y) \ge
F(x) + F'(x) (y – x),
\end{equation}
completing one direction of the proof.
To prove the other direction, showing that
\begin{equation}\label{eqn:convexOptimizationLecture6:140}
F(x) \ge F(x_0) + F'(x_0) (x – x_0),
\end{equation}
implies that \( F \) is convex. Take any \( x, y \in \textrm{dom} F \) and any \( \theta \in [0,1] \). Define
\begin{equation}\label{eqn:convexOptimizationLecture6:160}
z = \theta x + (1 -\theta) y,
\end{equation}
which is in \( \textrm{dom} F \) by assumption. We want to show that
\begin{equation}\label{eqn:convexOptimizationLecture6:180}
F(z) \le \theta F(x) + (1-\theta) F(y).
\end{equation}
By assumption
- \( F(x) \ge F(z) + F'(z) (x – z) \)
- \( F(y) \ge F(z) + F'(z) (y – z) \)
Compute
\begin{equation}\label{eqn:convexOptimizationLecture6:200}
\begin{aligned}
\theta F(x) + (1-\theta) F(y)
&\ge
\theta \lr{ F(z) + F'(z) (x – z) }
+ (1-\theta) \lr{ F(z) + F'(z) (y – z) } \\
&=
F(z) + F'(z) \lr{ \theta( x – z) + (1-\theta) (y-z) } \\
&=
F(z) + F'(z) \lr{ \theta x + (1-\theta) y – \theta z – (1 -\theta) z } \\
&=
F(z) + F'(z) \lr{ \theta x + (1-\theta) y – z} \\
&=
F(z) + F'(z) \lr{ z – z} \\
&= F(z).
\end{aligned}
\end{equation}
Proof of the 2nd order case for \( n = 1 \)
Want to prove that if
\begin{equation}\label{eqn:convexOptimizationLecture6:240}
F : \mathbb{R} \rightarrow \mathbb{R}
\end{equation}
is a convex function, then \( F”(x) \ge 0 \,\forall x \in \textrm{dom} F \).
By the first order conditions \( \forall x \ne y \in \textrm{dom} F \)
\begin{equation}\label{eqn:convexOptimizationLecture6:260}
\begin{aligned}
F(y) &\ge F(x) + F'(x) (y – x)
F(x) &\ge F(y) + F'(y) (x – y)
\end{aligned}
\end{equation}
Can combine and get
\begin{equation}\label{eqn:convexOptimizationLecture6:280}
F'(x) (y-x) \le F(y) – F(x) \le F'(y)(y-x)
\end{equation}
Subtract the two derivative terms for
\begin{equation}\label{eqn:convexOptimizationLecture6:340}
\frac{(F'(y) – F'(x))(y – x)}{(y – x)^2} \ge 0,
\end{equation}
or
\begin{equation}\label{eqn:convexOptimizationLecture6:300}
\frac{F'(y) – F'(x)}{y – x} \ge 0.
\end{equation}
In the limit as \( y \rightarrow x \), this is
\begin{equation}\label{eqn:convexOptimizationLecture6:320}
\boxed{
F”(x) \ge 0 \,\forall x \in \textrm{dom} F.
}
\end{equation}
Now prove the reverse condition:
If \( F”(x) \ge 0 \,\forall x \in \textrm{dom} F \subseteq \mathbb{R} \), implies that \( F : \mathbb{R} \rightarrow \mathbb{R} \) is convex.
Note that if \( F”(x) \ge 0 \), then \( F'(x) \) is non-decreasing in \( x \).
i.e. If \( x < y \), where \( x, y \in \textrm{dom} F\), then
\begin{equation}\label{eqn:convexOptimizationLecture6:360}
F'(x) \le F'(y).
\end{equation}
Consider any \( x,y \in \textrm{dom} F\) such that \( x < y \), where
\begin{equation}\label{eqn:convexOptimizationLecture6:380}
F(y) – F(x) = \int_x^y F'(t) dt \ge F'(x) \int_x^y 1 dt = F'(x) (y-x).
\end{equation}
This tells us that
\begin{equation}\label{eqn:convexOptimizationLecture6:400}
F(y) \ge F(x) + F'(x)(y – x),
\end{equation}
which is the first order condition. Similarly consider any \( x,y \in \textrm{dom} F\) such that \( x < y \), where
\begin{equation}\label{eqn:convexOptimizationLecture6:420}
F(y) – F(x) = \int_x^y F'(t) dt \le F'(y) \int_x^y 1 dt = F'(y) (y-x).
\end{equation}
This tells us that
\begin{equation}\label{eqn:convexOptimizationLecture6:440}
F(x) \ge F(y) + F'(y)(x – y).
\end{equation}
Vector proof:
\( F \) is convex iff \( F(\Bx + t \Bv) \) is convex \( \forall \Bx,\Bv \in \mathbb{R}^n, t \in \mathbb{R} \), keeping \( \Bx + t \Bv \in \textrm{dom} F\).
Let
\begin{equation}\label{eqn:convexOptimizationLecture6:460}
h(t ; \Bx, \Bv) = F(\Bx + t \Bv)
\end{equation}
then \( h(t) \) satisfies scalar first and second order conditions for all \( \Bx, \Bv \).
\begin{equation}\label{eqn:convexOptimizationLecture6:480}
h(t) = F(\Bx + t \Bv) = F(g(t)),
\end{equation}
where \( g(t) = \Bx + t \Bv \), where
\begin{equation}\label{eqn:convexOptimizationLecture6:500}
\begin{aligned}
F &: \mathbb{R}^n \rightarrow \mathbb{R} \\
g &: \mathbb{R} \rightarrow \mathbb{R}^n.
\end{aligned}
\end{equation}
This is expressing \( h(t) \) as a composition of two functions. By the first order condition for scalar functions we know that
\begin{equation}\label{eqn:convexOptimizationLecture6:520}
h(t) \ge h(0) + h'(0) t.
\end{equation}
Note that
\begin{equation}\label{eqn:convexOptimizationLecture6:540}
h(0) = \evalbar{F(\Bx + t \Bv)}{t = 0} = F(\Bx).
\end{equation}
Let’s figure out what \( h'(0) \) is. Recall hat for any \( \tilde{F} : \mathbb{R}^n \rightarrow \mathbb{R}^m \)
\begin{equation}\label{eqn:convexOptimizationLecture6:560}
D \tilde{F} \in \mathbb{R}^{m \times n},
\end{equation}
and
\begin{equation}\label{eqn:convexOptimizationLecture6:580}
{D \tilde{F}(\Bx)}_{ij} = \PD{x_j}{\tilde{F_i}(\Bx)}
\end{equation}
This is one function per row, for \( i \in [1,m], j \in [1,n] \). This gives
\begin{equation}\label{eqn:convexOptimizationLecture6:600}
\begin{aligned}
\frac{d}{dt} F(\Bx + \Bv t)
&=
\frac{d}{dt} F( g(t) ) \\
&=
\frac{d}{dt} h(t) \\
&= D h(t) \\
&= D F(g(t)) \cdot D g(t)
\end{aligned}
\end{equation}
The first matrix is in \( \mathbb{R}^{1\times n} \) whereas the second is in \( \mathbb{R}^{n\times 1} \), since \( F : \mathbb{R}^n \rightarrow \mathbb{R} \) and \( g : \mathbb{R} \rightarrow \mathbb{R}^n \). This gives
\begin{equation}\label{eqn:convexOptimizationLecture6:620}
\frac{d}{dt} F(\Bx + \Bv t)
= \evalbar{D F(\tilde{\Bx})}{\tilde{\Bx} = g(t)} \cdot D g(t).
\end{equation}
That first matrix is
\begin{equation}\label{eqn:convexOptimizationLecture6:640}
\begin{aligned}
\evalbar{D F(\tilde{\Bx})}{\tilde{\Bx} = g(t)}
&=
\evalbar{
\lr{\begin{bmatrix}
\PD{\tilde{x}_1}{ F(\tilde{\Bx})} &
\PD{\tilde{x}_2}{ F(\tilde{\Bx})} & \cdots
\PD{\tilde{x}_n}{ F(\tilde{\Bx})}
\end{bmatrix}
}}{ \tilde{\Bx} = g(t) = \Bx + t \Bv } \\
&=
\evalbar{
\lr{ \spacegrad F(\tilde{\Bx}) }^\T
}{
\tilde{\Bx} = g(t)
} \\
=
\lr{ \spacegrad F(g(t)) }^\T.
\end{aligned}
\end{equation}
The second Jacobian is
\begin{equation}\label{eqn:convexOptimizationLecture6:660}
D g(t)
=
D
\begin{bmatrix}
g_1(t) \\
g_2(t) \\
\vdots \\
g_n(t) \\
\end{bmatrix}
=
D
\begin{bmatrix}
x_1 + t v_1 \\
x_2 + t v_2 \\
\vdots \\
x_n + t v_n \\
\end{bmatrix}
=
\begin{bmatrix}
v_1 \\
v_1 \\
\vdots \\
v_n \\
\end{bmatrix}
=
\Bv.
\end{equation}
so
\begin{equation}\label{eqn:convexOptimizationLecture6:680}
h'(t) = D h(t) = \lr{ \spacegrad F(g(t))}^\T \Bv,
\end{equation}
and
\begin{equation}\label{eqn:convexOptimizationLecture6:700}
h'(0) = \lr{ \spacegrad F(g(0))}^\T \Bv
=
\lr{ \spacegrad F(\Bx)}^\T \Bv.
\end{equation}
Finally
\begin{equation}\label{eqn:convexOptimizationLecture6:720}
\begin{aligned}
F(\Bx + t \Bv)
&\ge h(0) + h'(0) t \\
&= F(\Bx) + \lr{ \spacegrad F(\Bx) }^\T (t \Bv) \\
&= F(\Bx) + \innerprod{ \spacegrad F(\Bx) }{ t \Bv}.
\end{aligned}
\end{equation}
Which is true for all \( \Bx, \Bx + t \Bv \in \textrm{dom} F \). Note that the quantity \( t \Bv \) is a shift.
Epigraph
Recall that if \( (\Bx, t) \in \textrm{epi} F \) then \( t \ge F(\Bx) \).
\begin{equation}\label{eqn:convexOptimizationLecture6:740}
t \ge F(\Bx) \ge F(\Bx_0) + \lr{\spacegrad F(\Bx_0) }^\T (\Bx – \Bx_0),
\end{equation}
or
\begin{equation}\label{eqn:convexOptimizationLecture6:760}
0 \ge
-(t – F(\Bx_0)) + \lr{\spacegrad F(\Bx_0) }^\T (\Bx – \Bx_0),
\end{equation}
In block matrix form
\begin{equation}\label{eqn:convexOptimizationLecture6:780}
0 \ge
\begin{bmatrix}
\lr{ \spacegrad F(\Bx_0) }^\T & -1
\end{bmatrix}
\begin{bmatrix}
\Bx – \Bx_0 \\
t – F(\Bx_0)
\end{bmatrix}
\end{equation}
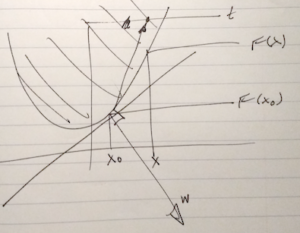
With \( \Bw =
\begin{bmatrix}
\lr{ \spacegrad F(\Bx_0) }^\T & -1
\end{bmatrix} \), the geometry of the epigraph relation to the half plane is sketched in fig. 3.
References
[1] Stephen Boyd and Lieven Vandenberghe. Convex optimization. Cambridge university press, 2004.