[Click here for a PDF of this post with nicer formatting]

In ancient times (i.e. 2nd year undergrad) I recall being very impressed with Tschebyscheff polynomials for designing lowpass filters. I’d used Tschebyscheff filters for the hardware we used for a speech recognition system our group built in the design lab. One of the benefits of these polynomials is that the oscillation in the $\Abs{x} < 1$ interval is strictly bounded. This same property, as well as the unbounded nature outside of the $[-1,1]$ interval turns out to have applications to antenna array design.

The Tschebyscheff polynomials are defined by

$$\begin{equation}\label{eqn:tschebyscheff:40} T_m(x) = \cos\lr{ m \cos^{-1} x }, \quad \Abs{x} < 1 \end{equation}$$ $$\begin{equation}\label{eqn:tschebyscheff:60} T_m(x) = \cosh\lr{ m \cosh^{-1} x }, \quad \Abs{x} > 1. \end{equation}$$

Range restrictions and hyperbolic form.

Prof. Eleftheriades’s notes made a point to point out the definition in the $\Abs{x} > 1$ interval, but that can also be viewed as a consequence instead of a definition if the range restriction is removed. For example, suppose $x = 7$, and let

$$\begin{equation}\label{eqn:tschebyscheff:160} \cos^{-1} 7 = \theta, \end{equation}$$

so
$$\begin{equation}\label{eqn:tschebyscheff:180} \begin{aligned} 7 &= \cos\theta \\ &= \frac{e^{i\theta} + e^{-i\theta}}{2} \\ &= \cosh(i\theta), \end{aligned} \end{equation}$$

or

$$\begin{equation}\label{eqn:tschebyscheff:200} -i \cosh^{-1} 7 = \theta. \end{equation}$$

$$\begin{equation}\label{eqn:tschebyscheff:220} \begin{aligned} T_m(7) &= \cos( -m i \cosh^{-1} 7 ) \\ &= \cosh( m \cosh^{-1} 7 ). \end{aligned} \end{equation}$$

The same argument clearly applies to any other value outside of the $\Abs{x} < 1$ range, so without any restrictions, these polynomials can be defined as just

$$\begin{equation}\label{eqn:tschebyscheff:260} \boxed{ T_m(x) = \cos\lr{ m \cos^{-1} x }. } \end{equation}$$

Polynomial nature.

Eq. $\ref{eqn:tschebyscheff:260}$ does not obviously look like a polynomial. Let’s proceed to verify the polynomial nature for the first couple values of $m$.

• $m = 0$. $$\begin{equation}\label{eqn:tschebyscheff:280} \begin{aligned} T_0(x) &= \cos( 0 \cos^{-1} x ) \\ &= \cos( 0 ) \\ &= 1. \end{aligned} \end{equation}$$
• $m = 1$. $$\begin{equation}\label{eqn:tschebyscheff:300} \begin{aligned} T_1(x) &= \cos( 1 \cos^{-1} x ) \\ &= x. \end{aligned} \end{equation}$$
• $m = 2$. $$\begin{equation}\label{eqn:tschebyscheff:320} \begin{aligned} T_2(x) &= \cos( 2 \cos^{-1} x ) \\ &= 2 \cos^2 \cos^{-1}(x) – 1 \\ &= 2 x^2 – 1. \end{aligned} \end{equation}$$

To examine the general case

$$\begin{equation}\label{eqn:tschebyscheff:340} \begin{aligned} T_m(x) &= \cos( m \cos^{-1} x ) \\ &= \textrm{Re} e^{ j m \cos^{-1} x } \\ &= \textrm{Re} \lr{ e^{ j\cos^{-1} x } }^m \\ &= \textrm{Re} \lr{ \cos\cos^{-1} x + j \sin\cos^{-1} x }^m \\ &= \textrm{Re} \lr{ x + j \sqrt{1 – x^2} }^m \\ &= \textrm{Re} \lr{ x^m + \binom{ m}{1} j x^{m-1} \lr{1 – x^2}^{1/2} – \binom{ m}{2} x^{m-2} \lr{1 – x^2}^{2/2} – \binom{ m}{3} j x^{m-3} \lr{1 – x^2}^{3/2} + \binom{ m}{4} x^{m-4} \lr{1 – x^2}^{4/2} + \cdots } \\ &= x^m – \binom{ m}{2} x^{m-2} \lr{1 – x^2} + \binom{ m}{4} x^{m-4} \lr{1 – x^2}^2 – \cdots \end{aligned} \end{equation}$$

This expansion was a bit cavaliar with the signs of the $\sin\cos^{-1} x = \sqrt{1 – x^2}$ terms, since the negative sign should be picked for the root when $x \in [-1,0]$. However, that doesn’t matter in the end since the real part operation selects only powers of two of this root.

The final result of the expansion above can be written

$$\begin{equation}\label{eqn:tschebyscheff:360} \boxed{ T_m(x) = \sum_{k = 0}^{\lfloor m/2 \rfloor} \binom{m}{2 k} (-1)^k x^{m – 2 k} \lr{1 – x^2}^k. } \end{equation}$$

This clearly shows the polynomial nature of these functions, and is also perfectly well defined for any value of $x$. The even and odd alternation with $m$ is also clear in this explicit expansion.

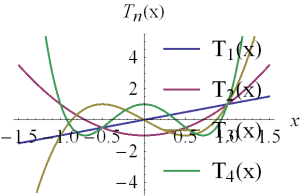
Plots

Properties

In [1] a few properties can be found for these polynomials

$$\begin{equation}\label{eqn:tschebyscheff:100} T_m(x) = 2 x T_{m-1} – T_{m-2} \end{equation}$$
$$\begin{equation}\label{eqn:tschebyscheff:420} 0 = \lr{ 1 – x^2 } \frac{d T_m(x)}{dx} + m x T_m(x) – m T_{m-1}(x) \end{equation}$$
$$\begin{equation}\label{eqn:tschebyscheff:400} 0 = \lr{ 1 – x^2 } \frac{d^2 T_m(x)}{dx^2} – x \frac{dT_m(x)}{dx} + m^2 T_{m}(x) \end{equation}$$
$$\begin{equation}\label{eqn:tschebyscheff:440} \int_{-1}^1 \inv{ \sqrt{1 – x^2} } T_m(x) T_n(x) dx = \left\{ \begin{array}{l l} 0 & \quad \mbox{if \( m \ne n \) } \\ \pi & \quad \mbox{if \( m = n = 0 \) } \\ \pi/2 & \quad \mbox{if \( m = n, m \ne 0 \) } \end{array} \right. \end{equation}$$

Recurrance relation.

Prove $\ref{eqn:tschebyscheff:100}$.

Answer.

To show this, let

$$\begin{equation}\label{eqn:tschebyscheff:460} x = \cos\theta. \end{equation}$$

$$\begin{equation}\label{eqn:tschebyscheff:580} 2 x T_{m-1} – T_{m-2} = 2 \cos\theta \cos((m-1) \theta) – \cos((m-2)\theta). \end{equation}$$

Recall the cosine addition formulas

$$\begin{equation}\label{eqn:tschebyscheff:540} \begin{aligned} \cos( a + b ) &= \textrm{Re} e^{j(a + b)} \\ &= \textrm{Re} e^{ja} e^{jb} \\ &= \textrm{Re} \lr{ \cos a + j \sin a } \lr{ \cos b + j \sin b } \\ &= \cos a \cos b – \sin a \sin b. \end{aligned} \end{equation}$$

Applying this gives

$$\begin{equation}\label{eqn:tschebyscheff:600} \begin{aligned} 2 x T_{m-1} – T_{m-2} &= 2 \cos\theta \Biglr{ \cos(m\theta)\cos\theta +\sin(m\theta) \sin\theta } – \Biglr{ \cos(m\theta)\cos(2\theta) + \sin(m\theta) \sin(2\theta) } \\ &= 2 \cos\theta \Biglr{ \cos(m\theta)\cos\theta +\sin(m\theta)\sin\theta) } – \Biglr{ \cos(m\theta)(\cos^2 \theta – \sin^2 \theta) + 2 \sin(m\theta) \sin\theta \cos\theta } \\ &= \cos(m\theta) \lr{ \cos^2\theta + \sin^2\theta } \\ &= T_m(x). \end{aligned} \end{equation}$$

First order LDE relation.

Prove $\ref{eqn:tschebyscheff:420}$.

Answer.

To show this, again, let

$$\begin{equation}\label{eqn:tschebyscheff:470} x = \cos\theta. \end{equation}$$

Observe that

$$\begin{equation}\label{eqn:tschebyscheff:480} 1 = -\sin\theta \frac{d\theta}{dx}, \end{equation}$$

so

$$\begin{equation}\label{eqn:tschebyscheff:500} \begin{aligned} \frac{d}{dx} &= \frac{d\theta}{dx} \frac{d}{d\theta} \\ &= -\frac{1}{\sin\theta} \frac{d}{d\theta}. \end{aligned} \end{equation}$$

Plugging this in gives

$$\begin{equation}\label{eqn:tschebyscheff:520} \begin{aligned} \lr{ 1 – x^2} &\frac{d}{dx} T_m(x) + m x T_m(x) – m T_{m-1}(x) \\ &= \sin^2\theta \lr{ -\frac{1}{\sin\theta} \frac{d}{d\theta}} \cos( m \theta ) + m \cos\theta \cos( m \theta ) – m \cos( (m-1)\theta ) \\ &= -\sin\theta (-m \sin(m \theta)) + m \cos\theta \cos( m \theta ) – m \cos( (m-1)\theta ). \end{aligned} \end{equation}$$

Applying the cosine addition formula $\ref{eqn:tschebyscheff:540}$ gives

$$\begin{equation}\label{eqn:tschebyscheff:560} m \lr{ \sin\theta \sin(m \theta) + \cos\theta \cos( m \theta ) } – m \lr{ \cos( m \theta) \cos\theta + \sin( m \theta ) \sin\theta } =0. \end{equation}$$

} % answer

Second order LDE relation.

Prove $\ref{eqn:tschebyscheff:400}$.

Answer.

This follows the same way. The first derivative was

$$\begin{equation}\label{eqn:tschebyscheff:640} \begin{aligned} \frac{d T_m(x)}{dx} &= -\inv{\sin\theta} \frac{d}{d\theta} \cos(m\theta) \\ &= -\inv{\sin\theta} (-m) \sin(m\theta) \\ &= m \inv{\sin\theta} \sin(m\theta), \end{aligned} \end{equation}$$

so the second derivative is

$$\begin{equation}\label{eqn:tschebyscheff:620} \begin{aligned} \frac{d^2 T_m(x)}{dx^2} &= -m \inv{\sin\theta} \frac{d}{d\theta} \inv{\sin\theta} \sin(m\theta) \\ &= -m \inv{\sin\theta} \lr{ -\frac{\cos\theta}{\sin^2\theta} \sin(m\theta) + \inv{\sin\theta} m \cos(m\theta) }. \end{aligned} \end{equation}$$

Putting all the pieces together gives

$$\begin{equation}\label{eqn:tschebyscheff:660} \begin{aligned} \lr{ 1 – x^2 } &\frac{d^2 T_m(x)}{dx^2} – x \frac{dT_m(x)}{dx} + m^2 T_{m}(x) \\ &= m \lr{ \frac{\cos\theta}{\sin\theta} \sin(m\theta) – m \cos(m\theta) } – \cos\theta m \inv{\sin\theta} \sin(m\theta) + m^2 \cos(m \theta) \\ &= 0. \end{aligned} \end{equation}$$

Orthogonality relation

Prove $\ref{eqn:tschebyscheff:440}$.

Answer.

First consider the 0,0 inner product, making an $x = \cos\theta$, so that $dx = -\sin\theta d\theta$

$$\begin{equation}\label{eqn:tschebyscheff:680} \begin{aligned} \innerprod{T_0}{T_0} &= \int_{-1}^1 \inv{\lr{1-x^2}^{1/2}} dx \\ &= \int_{-\pi}^0 \lr{-\inv{\sin\theta}} -\sin\theta d\theta \\ &= 0 – (-\pi) \\ &= \pi. \end{aligned} \end{equation}$$

Note that since the $[-\pi, 0]$ interval was chosen, the negative root of $\sin^2\theta = 1 – x^2$ was chosen, since $\sin\theta$ is negative in that interval.

The m,m inner product with $m \ne 0$ is

$$\begin{equation}\label{eqn:tschebyscheff:700} \begin{aligned} \innerprod{T_m}{T_m} &= \int_{-1}^1 \inv{\lr{1-x^2}^{1/2}} \lr{ T_m(x)}^2 dx \\ &= \int_{-\pi}^0 \lr{-\inv{\sin\theta}} \cos^2(m\theta) -\sin\theta d\theta \\ &= \int_{-\pi}^0 \cos^2(m\theta) d\theta \\ &= \inv{2} \int_{-\pi}^0 \lr{ \cos(2 m\theta) + 1 } d\theta \\ &= \frac{\pi}{2}. \end{aligned} \end{equation}$$

So far so good. For $m \ne n$ the inner product is

$$\begin{equation}\label{eqn:tschebyscheff:720} \begin{aligned} \innerprod{T_m}{T_m} &= \int_{-\pi}^0 \cos(m\theta) \cos(n\theta) d\theta \\ &= \inv{4} \int_{-\pi}^0 \lr{ e^{j m \theta} + e^{-j m \theta} } \lr{ e^{j n \theta} + e^{-j n \theta} } d\theta \\ &= \inv{4} \int_{-\pi}^0 \lr{ e^{j (m + n) \theta} +e^{-j (m + n) \theta} +e^{j (m – n) \theta} +e^{j (-m + n) \theta} } d\theta \\ &= \inv{2} \int_{-\pi}^0 \lr{ \cos( (m + n)\theta ) +\cos( (m – n)\theta ) } d\theta \\ &= \inv{2} \evalrange{ \lr{ \frac{\sin( (m + n)\theta )}{ m + n } +\frac{\sin( (m – n)\theta )}{ m – n} } }{-\pi}{0} \\ &= 0. \end{aligned} \end{equation}$$

References

[1] M. Abramowitz and I.A. Stegun. Handbook of mathematical functions with formulas, graphs, and mathematical tables, volume 55. Dover publications, 1964.