As mentioned previously, using geometric algebra we can convert the iterative equation for the Mandelbrot set from complex number form
\begin{equation}
z \rightarrow z^2 + c,
\end{equation}
to an equivalent vector form
\begin{equation}
\mathbf{x} \rightarrow \mathbf{x} \mathbf{e} \mathbf{x} + \mathbf{c},
\end{equation}
where \( \mathbf{e} \) represents the x-axis (say). Geometrically, each iteration takes \( \mathbf{e} \) and reflects it about the direction of \( \mathbf{x} \), then scales that by \( \mathbf{x}^2 \) and adds \( \mathbf{c} \).
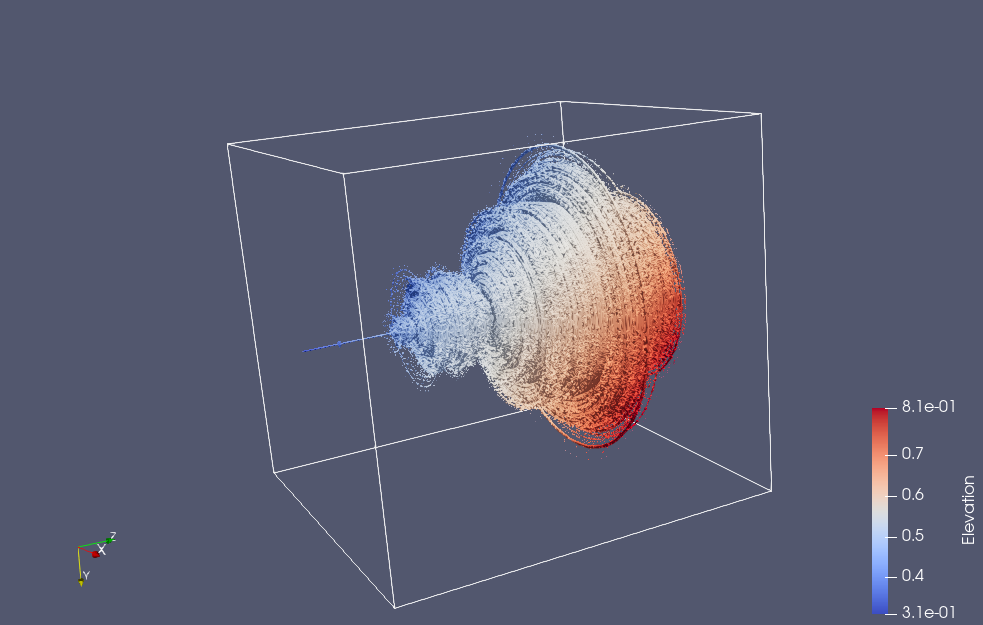
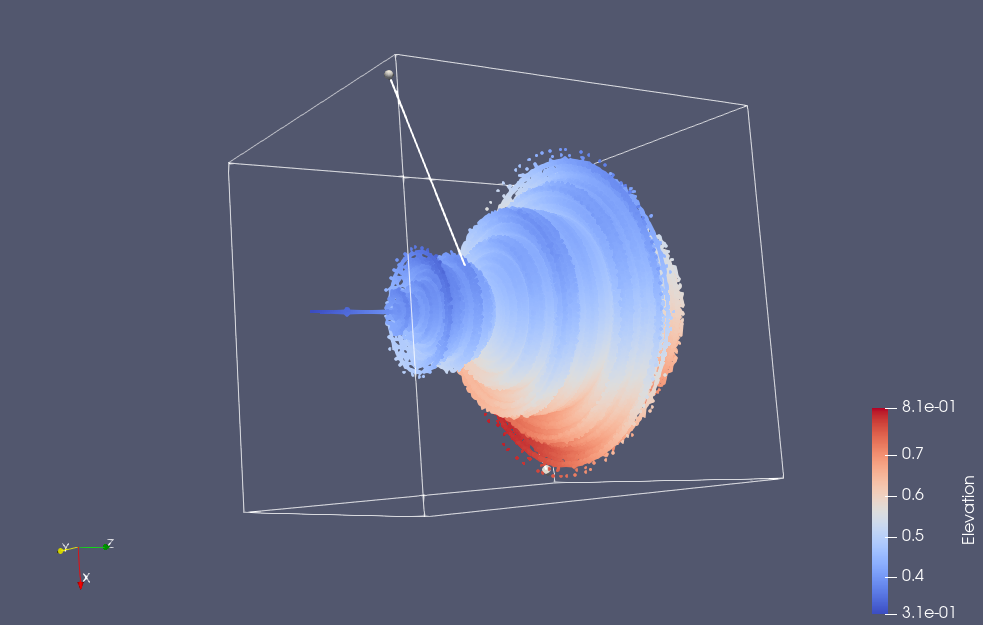
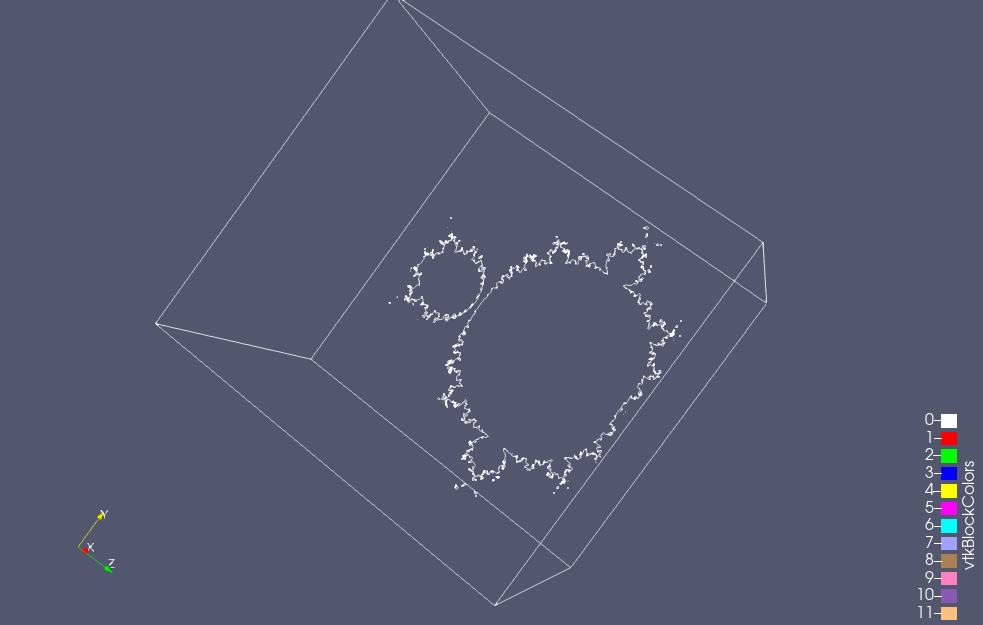
To get the usual 2D Mandelbrot set, one iterates with vectors that lie only in the x-y plane, but we can treat the Mandelbrot set as a 3D solid if we remove the x-y plane restriction.
Last time I animated slices of the 3D set, but after a whole lot of messing around I managed to save the data for all the interior points of the 3D set in netCDF format, and render the solid using Paraview. Paraview has tons of filters available, and experimenting with them is pretty time consuming, but here are some initial screenshots of the 3D Mandelbrot set:
It’s interesting that much of the characteristic detail of the Mandelbrot set is not visible in the 3D volume, but if we slice that volume, you can then you can see it again. Here’s a slice taken close to the z=0 plane (but far enough that the “CN tower” portion of the set is not visible)
You can also see some of that detail if the opacity of the rendering is turned way down:
If you look carefully at the images above, you’ll see that the axis labels are wrong. I think that I’ve screwed up one of the stride related parameters to my putVar call, and I end up with x+z transposed in the axes labels when visualized.