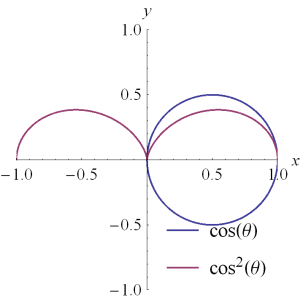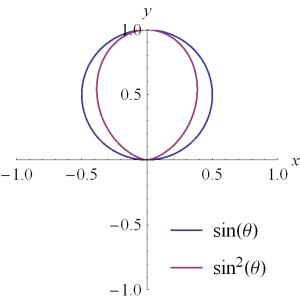[Click here for a PDF of this post with nicer formatting]
This is my first set of notes for the UofT course ECE1229, Advanced Antenna Theory, taught by Prof. Eleftheriades, covering ch. 2 [1] content.
Unlike most of the other classes I have taken, I am not attempting to take comprehensive notes for this class. The class is taught on slides that match the textbook so closely, there is little value to me taking notes that just replicate the text. Instead, I am annotating my copy of textbook with little details instead. My usual notes collection for the class will contain musings of details that were unclear, or in some cases, details that were provided in class, but are not in the text (and too long to pencil into my book.)
Poynting vector
The Poynting vector was written in an unfamiliar form
\begin{equation}\label{eqn:chapter2Notes:560}
\boldsymbol{\mathcal{W}} = \boldsymbol{\mathcal{E}} \cross \boldsymbol{\mathcal{H}}.
\end{equation}
I can roll with the use of a different symbol (i.e. not \(\BS\)) for the Poynting vector, but I’m used to seeing a \( \frac{c}{4\pi} \) factor ([6] and [5]). I remembered something like that in SI units too, so was slightly confused not to see it here.
Per [3] that something is a \( \mu_0 \), as in
\begin{equation}\label{eqn:chapter2Notes:580}
\boldsymbol{\mathcal{W}} = \inv{\mu_0} \boldsymbol{\mathcal{E}} \cross \boldsymbol{\mathcal{B}}.
\end{equation}
Note that the use of \( \boldsymbol{\mathcal{H}} \) instead of \( \boldsymbol{\mathcal{B}} \) is what wipes out the requirement for the \( \frac{1}{\mu_0} \) term since \( \boldsymbol{\mathcal{H}} = \boldsymbol{\mathcal{B}}/\mu_0 \), assuming linear media, and no magnetization.
Typical far-field radiation intensity
It was mentioned that
\begin{equation}\label{eqn:advancedantennaL1:20}
U(\theta, \phi)
=
\frac{r^2}{2 \eta_0} \Abs{ \BE( r, \theta, \phi) }^2
=
\frac{1}{2 \eta_0} \lr{ \Abs{ E_\theta(\theta, \phi) }^2 + \Abs{ E_\phi(\theta, \phi) }^2},
\end{equation}
where the intrinsic impedance of free space is
\begin{equation}\label{eqn:advancedantennaL1:480}
\eta_0 = \sqrt{\frac{\mu_0}{\epsilon_0}} = 377 \Omega.
\end{equation}
(this is also eq. 2-19 in the text.)
To get an understanding where this comes from, consider the far field radial solutions to the electric and magnetic dipole problems, which have the respective forms (from [3]) of
\begin{equation}\label{eqn:chapter2Notes:740}
\begin{aligned}
\boldsymbol{\mathcal{E}} &= -\frac{\mu_0 p_0 \omega^2 }{4 \pi } \frac{\sin\theta}{r} \cos\lr{w t – k r} \thetacap \\
\boldsymbol{\mathcal{B}} &= -\frac{\mu_0 p_0 \omega^2 }{4 \pi c} \frac{\sin\theta}{r} \cos\lr{w t – k r} \phicap \\
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:chapter2Notes:760}
\begin{aligned}
\boldsymbol{\mathcal{E}} &= \frac{\mu_0 m_0 \omega^2 }{4 \pi c} \frac{\sin\theta}{r} \cos\lr{w t – k r} \phicap \\
\boldsymbol{\mathcal{B}} &= -\frac{\mu_0 m_0 \omega^2 }{4 \pi c^2} \frac{\sin\theta}{r} \cos\lr{w t – k r} \thetacap \\
\end{aligned}
\end{equation}
In neither case is there a component in the direction of propagation, and in both cases (using \( \mu_0 \epsilon_0 = 1/c^2\))
\begin{equation}\label{eqn:chapter2Notes:780}
\Abs{\boldsymbol{\mathcal{H}}}
= \frac{\Abs{\boldsymbol{\mathcal{E}}}}{\mu_0 c}
= \Abs{\boldsymbol{\mathcal{E}}} \sqrt{\frac{\epsilon_0}{\mu_0}}
= \inv{\eta_0}\Abs{\boldsymbol{\mathcal{E}}} .
\end{equation}
A superposition of the phasors for such dipole fields, in the far field, will have the form
\begin{equation}\label{eqn:chapter2Notes:800}
\begin{aligned}
\BE &= \inv{r} \lr{ E_\theta(\theta, \phi) \thetacap + E_\phi(\theta, \phi) \phicap } \\
\BB &= \inv{r c} \lr{ E_\theta(\theta, \phi) \thetacap – E_\phi(\theta, \phi) \phicap },
\end{aligned}
\end{equation}
with a corresponding time averaged Poynting vector
\begin{equation}\label{eqn:chapter2Notes:820}
\begin{aligned}
\BW_{\textrm{av}}
&= \inv{2 \mu_0} \BE \cross \BB^\conj \\
&=
\inv{2 \mu_0 c r^2}
\lr{ E_\theta \thetacap + E_\phi \phicap } \cross
\lr{ E_\theta^\conj \thetacap – E_\phi^\conj \phicap } \\
&=
\frac{\thetacap \cross \phicap}{2 \mu_0 c r^2}
\lr{ \Abs{E_\theta}^2 + \Abs{E_\phi}^2 } \\
&=
\frac{\rcap}{2 \eta_0 r^2}
\lr{ \Abs{E_\theta}^2 + \Abs{E_\phi}^2 },
\end{aligned}
\end{equation}
verifying \ref{eqn:advancedantennaL1:20} for a superposition of electric and magnetic dipole fields. This can likely be shown for more general fields too.
Field plots
We can plot the fields, or intensity (or log plots in dB of these).
It is pointed out in [3] that when there is \( r \) dependence these plots are done by considering the values of at fixed \( r \).
The field plots are conceptually the simplest, since that vector parameterizes
a surface. Any such radial field with magnitude \( f(r, \theta, \phi) \) can
be plotted in Mathematica in the \( \phi = 0 \) plane at \( r = r_0 \), or in
3D (respectively, but also at \( r = r_0\)) with code like that of the
following listing

Intensity plots can use the same code, with the only difference being the interpretation. The surface doesn’t represent the value of a vector valued radial function, but is the magnitude of a scalar valued function evaluated at \( f( r_0, \theta, \phi) \).
The surfaces for \( U = \sin\theta, \sin^2\theta \) in the plane are parametrically plotted in fig. 2, and for cosines in fig. 1 to compare with textbook figures.
fig 1. Cosinusoidal radiation intensities
fig 2. Sinusoidal radiation intensities
Visualizations of \( U = \sin^2 \theta\) and \( U = \cos^2 \theta\) can be found in fig. 3 and fig. 4 respectively. Even for such simple functions these look pretty cool.
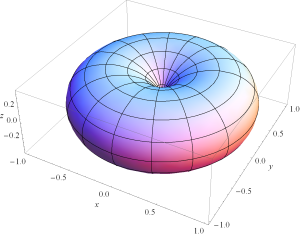
fig 3. Square sinusoidal radiation intensity

fig 4. Square cosinusoidal radiation intensity
dB vs dBi
Note that dBi is used to indicate that the gain is with respect to an “isotropic” radiator.
This is detailed more in [2].
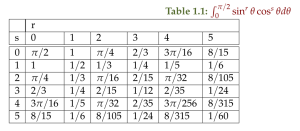
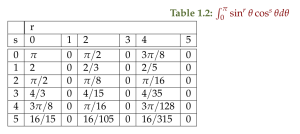
Trig integrals
Tables 1.1 and 1.2 produced with tableOfTrigIntegrals.nb have some of the sine and cosine integrals that are pervasive in this chapter.
Polarization vectors
The text introduces polarization vectors \( \rhocap \) , but doesn’t spell out their form. Consider a plane wave field of the form
\begin{equation}\label{eqn:chapter2Notes:840}
\BE
=
E_x e^{j \phi_x} e^{j \lr{ \omega t – k z }} \xcap
+
E_y e^{j \phi_y} e^{j \lr{ \omega t – k z }} \ycap.
\end{equation}
The \( x, y \) plane directionality of this phasor can be written
\begin{equation}\label{eqn:chapter2Notes:860}
\Brho =
E_x e^{j \phi_x} \xcap
+
E_y e^{j \phi_y} \ycap,
\end{equation}
so that
\begin{equation}\label{eqn:chapter2Notes:880}
\BE = \Brho e^{j \lr{ \omega t – k z }}.
\end{equation}
Separating this direction and magnitude into factors
\begin{equation}\label{eqn:chapter2Notes:900}
\Brho = \Abs{\BE} \rhocap,
\end{equation}
allows the phasor to be expressed as
\begin{equation}\label{eqn:chapter2Notes:920}
\BE = \rhocap \Abs{\BE} e^{j \lr{ \omega t – k z }}.
\end{equation}
As an example, suppose that \( E_x = E_y \), and set \( \phi_x = 0 \). Then
\begin{equation}\label{eqn:chapter2Notes:940}
\rhocap = \xcap + \ycap e^{j \phi_y}.
\end{equation}
Phasor power
In section 2.13 the phasor power is written as
\begin{equation}\label{eqn:chapter2Notes:620}
I^2 R/2,
\end{equation}
where \( I, R \) are the magnitudes of phasors in the circuit.
I vaguely recall this relation, but had to refer back to [4] for the details.
This relation expresses average power over a period associated with the frequency of the phasor
\begin{equation}\label{eqn:chapter2Notes:640}
\begin{aligned}
P
&= \inv{T} \int_{t_0}^{t_0 + T} p(t) dt \\
&= \inv{T} \int_{t_0}^{t_0 + T} \Abs{\BV} \cos\lr{ \omega t + \phi_V }
\Abs{\BI} \cos\lr{ \omega t + \phi_I} dt \\
&= \inv{T} \int_{t_0}^{t_0 + T} \Abs{\BV} \Abs{\BI}
\lr{
\cos\lr{ \phi_V – \phi_I } + \cos\lr{ 2 \omega t + \phi_V + \phi_I}
}
dt \\
&= \inv{2} \Abs{\BV} \Abs{\BI} \cos\lr{ \phi_V – \phi_I }.
\end{aligned}
\end{equation}
Introducing the impedance for this circuit element
\begin{equation}\label{eqn:chapter2Notes:660}
\BZ = \frac{ \Abs{\BV} e^{j\phi_V} }{ \Abs{\BI} e^{j\phi_I} } = \frac{\Abs{\BV}}{\Abs{\BI}} e^{j\lr{\phi_V – \phi_I}},
\end{equation}
this average power can be written in phasor form
\begin{equation}\label{eqn:chapter2Notes:680}
\BP = \inv{2} \Abs{\BI}^2 \BZ,
\end{equation}
with
\begin{equation}\label{eqn:chapter2Notes:700}
P = \textrm{Re} \BP.
\end{equation}
Observe that we have to be careful to use the absolute value of the current phasor \( \BI \), since \( \BI^2 \) differs in phase from \( \Abs{\BI}^2 \). This explains the conjugation in the [4] definition of complex power, which had the form
\begin{equation}\label{eqn:chapter2Notes:720}
\BS = \BV_{\textrm{rms}} \BI^\conj_{\textrm{rms}}.
\end{equation}
Radar cross section examples
Flat plate.
\begin{equation}\label{eqn:chapter2Notes:960}
\sigma_{\textrm{max}} = \frac{4 \pi \lr{L W}^2}{\lambda^2}
\end{equation}
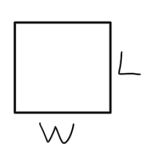
fig. 6. Square geometry for RCS example.
Sphere.
In the optical limit the radar cross section for a sphere
fig. 7. Sphere geometry for RCS example.
\begin{equation}\label{eqn:chapter2Notes:980}
\sigma_{\textrm{max}} = \pi r^2
\end{equation}
Note that this is smaller than the physical area \( 4 \pi r^2 \).
Cylinder.
fig. 8. Cylinder geometry for RCS example.
\begin{equation}\label{eqn:chapter2Notes:1000}
\sigma_{\textrm{max}} = \frac{ 2 \pi r h^2}{\lambda}
\end{equation}
Tridedral corner reflector
fig. 9. Trihedral corner reflector geometry for RCS example.
\begin{equation}\label{eqn:chapter2Notes:1020}
\sigma_{\textrm{max}} = \frac{ 4 \pi L^4}{3 \lambda^2}
\end{equation}
Scattering from a sphere vs frequency
Frequency dependence of spherical scattering is sketched in fig. 10.
- Low frequency (or small particles): Rayleigh\begin{equation}\label{eqn:chapter2Notes:1040}
\sigma = \lr{\pi r^2} 7.11 \lr{\kappa r}^4, \qquad \kappa = 2 \pi/\lambda.
\end{equation}
- Mie scattering (resonance),\begin{equation}\label{eqn:chapter2Notes:1060}
\sigma_{\textrm{max}}(A) = 4 \pi r^2
\end{equation}
\begin{equation}\label{eqn:chapter2Notes:1080}
\sigma_{\textrm{max}}(B) = 0.26 \pi r^2.
\end{equation}
- optical limit ( \(r \gg \lambda\) )\begin{equation}\label{eqn:chapter2Notes:1100}
\sigma = \pi r^2.
\end{equation}
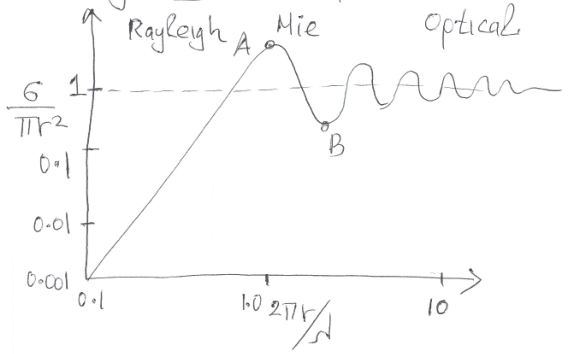
fig 10. Scattering from a sphere vs frequency (from Prof. Eleftheriades’ class notes).
FIXME: Do I have a derivation of this in my optics notes?
Notation
- Time average.
Both Prof. Eleftheriades
and the text [1] use square brackets \( [\cdots] \) for time averages, not \( <\cdots> \). Was that an engineering convention?
- Prof. Eleftheriades
writes \(\Omega\) as a circle floating above a face up square bracket, as in fig. 1, and \( \sigma \) like a number 6, as in fig. 1.
- Bold vectors are usually phasors, with (bold) calligraphic script used for the time domain fields. Example: \( \BE(x,y,z,t) = \ecap E(x,y) e^{j \lr{\omega t – k z}}, \boldsymbol{\mathcal{E}}(x, y, z, t) = \textrm{Re} \BE \).

fig. 11. Prof. handwriting decoder ring: Omega

fig 12. Prof. handwriting decoder ring: sigma
References
[1] Constantine A Balanis. Antenna theory: analysis and design. John Wiley \& Sons, 3rd edition, 2005.
[3] David Jeffrey Griffiths and Reed College. Introduction to electrodynamics. Prentice hall Upper Saddle River, NJ, 3rd edition, 1999.
[4] J.D. Irwin. Basic Engineering Circuit Analysis. MacMillian, 1993.
[5] JD Jackson. Classical Electrodynamics. John Wiley and Sons, 2nd edition, 1975.
[6] L.D. Landau and E.M. Lifshitz. The classical theory of fields. Butterworth-Heinemann, 1980. ISBN 0750627689.
Like this:
Like Loading...