Dirac basis

A multivector Lagrangian for Maxwell’s equation: A summary of previous exploration.

June 21, 2022 math and physics play , , , , , , , , , , , , , , , , , , , ,

This summarizes the significant parts of the last 8 blog posts.

[Click here for a PDF version of this post]

STA form of Maxwell’s equation.

Maxwell’s equations, with electric and fictional magnetic sources (useful for antenna theory and other engineering applications), are
\begin{equation}\label{eqn:maxwellLagrangian:220}
\begin{aligned}
\spacegrad \cdot \BE &= \frac{\rho}{\epsilon} \\
\spacegrad \cross \BE &= – \BM – \mu \PD{t}{\BH} \\
\spacegrad \cdot \BH &= \frac{\rho_\txtm}{\mu} \\
\spacegrad \cross \BH &= \BJ + \epsilon \PD{t}{\BE}.
\end{aligned}
\end{equation}
We can assemble these into a single geometric algebra equation,
\begin{equation}\label{eqn:maxwellLagrangian:240}
\lr{ \spacegrad + \inv{c} \PD{t}{} } F = \eta \lr{ c \rho – \BJ } + I \lr{ c \rho_{\mathrm{m}} – \BM },
\end{equation}
where \( F = \BE + \eta I \BH = \BE + I c \BB \), \( c = 1/\sqrt{\mu\epsilon}, \eta = \sqrt{(\mu/\epsilon)} \).

By multiplying through by \( \gamma_0 \), making the identification \( \Be_k = \gamma_k \gamma_0 \), and
\begin{equation}\label{eqn:maxwellLagrangian:300}
\begin{aligned}
J^0 &= \frac{\rho}{\epsilon}, \quad J^k = \eta \lr{ \BJ \cdot \Be_k }, \quad J = J^\mu \gamma_\mu \\
M^0 &= c \rho_{\mathrm{m}}, \quad M^k = \BM \cdot \Be_k, \quad M = M^\mu \gamma_\mu \\
\grad &= \gamma^\mu \partial_\mu,
\end{aligned}
\end{equation}
we find the STA form of Maxwell’s equation, including magnetic sources
\begin{equation}\label{eqn:maxwellLagrangian:320}
\grad F = J – I M.
\end{equation}

Decoupling the electric and magnetic fields and sources.

We can utilize two separate four-vector potential fields to split Maxwell’s equation into two parts. Let
\begin{equation}\label{eqn:maxwellLagrangian:1740}
F = F_{\mathrm{e}} + I F_{\mathrm{m}},
\end{equation}
where
\begin{equation}\label{eqn:maxwellLagrangian:1760}
\begin{aligned}
F_{\mathrm{e}} &= \grad \wedge A \\
F_{\mathrm{m}} &= \grad \wedge K,
\end{aligned}
\end{equation}
and \( A, K \) are independent four-vector potential fields. Plugging this into Maxwell’s equation, and employing a duality transformation, gives us two coupled vector grade equations
\begin{equation}\label{eqn:maxwellLagrangian:1780}
\begin{aligned}
\grad \cdot F_{\mathrm{e}} – I \lr{ \grad \wedge F_{\mathrm{m}} } &= J \\
\grad \cdot F_{\mathrm{m}} + I \lr{ \grad \wedge F_{\mathrm{e}} } &= M.
\end{aligned}
\end{equation}
However, since \( \grad \wedge F_{\mathrm{m}} = \grad \wedge F_{\mathrm{e}} = 0 \), by construction, the curls above are killed. We may also add in \( \grad \wedge F_{\mathrm{e}} = 0 \) and \( \grad \wedge F_{\mathrm{m}} = 0 \) respectively, yielding two independent gradient equations
\begin{equation}\label{eqn:maxwellLagrangian:1810}
\begin{aligned}
\grad F_{\mathrm{e}} &= J \\
\grad F_{\mathrm{m}} &= M,
\end{aligned}
\end{equation}
one for each of the electric and magnetic sources and their associated fields.

Tensor formulation.

The electromagnetic field \( F \), is a vector-bivector multivector in the multivector representation of Maxwell’s equation, but is a bivector in the STA representation. The split of \( F \) into it’s electric and magnetic field components is observer dependent, but we may write it without reference to a specific observer frame as
\begin{equation}\label{eqn:maxwellLagrangian:1830}
F = \inv{2} \gamma_\mu \wedge \gamma_\nu F^{\mu\nu},
\end{equation}
where \( F^{\mu\nu} \) is an arbitrary antisymmetric 2nd rank tensor. Maxwell’s equation has a vector and trivector component, which may be split out explicitly using grade selection, to find
\begin{equation}\label{eqn:maxwellLagrangian:360}
\begin{aligned}
\grad \cdot F &= J \\
\grad \wedge F &= -I M.
\end{aligned}
\end{equation}
Further dotting and wedging these equations with \( \gamma^\mu \) allows for extraction of scalar relations
\begin{equation}\label{eqn:maxwellLagrangian:460}
\partial_\nu F^{\nu\mu} = J^{\mu}, \quad \partial_\nu G^{\nu\mu} = M^{\mu},
\end{equation}
where \( G^{\mu\nu} = -(1/2) \epsilon^{\mu\nu\alpha\beta} F_{\alpha\beta} \) is also an antisymmetric 2nd rank tensor.

If we treat \( F^{\mu\nu} \) and \( G^{\mu\nu} \) as independent fields, this pair of equations is the coordinate equivalent to \ref{eqn:maxwellLagrangian:1760}, also decoupling the electric and magnetic source contributions to Maxwell’s equation.

Coordinate representation of the Lagrangian.

As observed above, we may choose to express the decoupled fields as curls \( F_{\mathrm{e}} = \grad \wedge A \) or \( F_{\mathrm{m}} = \grad \wedge K \). The coordinate expansion of either field component, given such a representation, is straight forward. For example
\begin{equation}\label{eqn:maxwellLagrangian:1850}
\begin{aligned}
F_{\mathrm{e}}
&= \lr{ \gamma_\mu \partial^\mu } \wedge \lr{ \gamma_\nu A^\nu } \\
&= \inv{2} \lr{ \gamma_\mu \wedge \gamma_\nu } \lr{ \partial^\mu A^\nu – \partial^\nu A^\mu }.
\end{aligned}
\end{equation}

We make the identification \( F^{\mu\nu} = \partial^\mu A^\nu – \partial^\nu A^\mu \), the usual definition of \( F^{\mu\nu} \) in the tensor formalism. In that tensor formalism, the Maxwell Lagrangian is
\begin{equation}\label{eqn:maxwellLagrangian:1870}
\LL = – \inv{4} F_{\mu\nu} F^{\mu\nu} – A_\mu J^\mu.
\end{equation}
We may show this though application of the Euler-Lagrange equations
\begin{equation}\label{eqn:maxwellLagrangian:600}
\PD{A_\mu}{\LL} = \partial_\nu \PD{(\partial_\nu A_\mu)}{\LL}.
\end{equation}
\begin{equation}\label{eqn:maxwellLagrangian:1930}
\begin{aligned}
\PD{(\partial_\nu A_\mu)}{\LL}
&= -\inv{4} (2) \lr{ \PD{(\partial_\nu A_\mu)}{F_{\alpha\beta}} } F^{\alpha\beta} \\
&= -\inv{2} \delta^{[\nu\mu]}_{\alpha\beta} F^{\alpha\beta} \\
&= -\inv{2} \lr{ F^{\nu\mu} – F^{\mu\nu} } \\
&= F^{\mu\nu}.
\end{aligned}
\end{equation}
So \( \partial_\nu F^{\nu\mu} = J^\mu \), the equivalent of \( \grad \cdot F = J \), as expected.

Coordinate-free representation and variation of the Lagrangian.

Because
\begin{equation}\label{eqn:maxwellLagrangian:200}
F^2 =
-\inv{2}
F^{\mu\nu} F_{\mu\nu}
+
\lr{ \gamma_\alpha \wedge \gamma^\beta }
F_{\alpha\mu}
F^{\beta\mu}
+
\frac{I}{4}
\epsilon_{\mu\nu\alpha\beta} F^{\mu\nu} F^{\alpha\beta},
\end{equation}
we may express the Lagrangian \ref{eqn:maxwellLagrangian:1870} in a coordinate free representation
\begin{equation}\label{eqn:maxwellLagrangian:1890}
\LL = \inv{2} F \cdot F – A \cdot J,
\end{equation}
where \( F = \grad \wedge A \).

We will now show that it is also possible to apply the variational principle to the following multivector Lagrangian
\begin{equation}\label{eqn:maxwellLagrangian:1910}
\LL = \inv{2} F^2 – A \cdot J,
\end{equation}
and recover the geometric algebra form \( \grad F = J \) of Maxwell’s equation in it’s entirety, including both vector and trivector components in one shot.

We will need a few geometric algebra tools to do this.

The first such tool is the notational freedom to let the gradient act bidirectionally on multivectors to the left and right. We will designate such action with over-arrows, sometimes also using braces to limit the scope of the action in question. If \( Q, R \) are multivectors, then the bidirectional action of the gradient in a \( Q, R \) sandwich is
\begin{equation}\label{eqn:maxwellLagrangian:1950}
\begin{aligned}
Q \lrgrad R
&= Q \lgrad R + Q \rgrad R \\
&= \lr{ Q \gamma^\mu \lpartial_\mu } R + Q \lr{ \gamma^\mu \rpartial_\mu R } \\
&= \lr{ \partial_\mu Q } \gamma^\mu R + Q \gamma^\mu \lr{ \partial_\mu R }.
\end{aligned}
\end{equation}
In the final statement, the partials are acting exclusively on \( Q \) and \( R \) respectively, but the \( \gamma^\mu \) factors must remain in place, as they do not necessarily commute with any of the multivector factors.

This bidirectional action is a critical aspect of the Fundamental Theorem of Geometric calculus, another tool that we will require. The specific form of that theorem that we will utilize here is
\begin{equation}\label{eqn:maxwellLagrangian:1970}
\int_V Q d^4 \Bx \lrgrad R = \int_{\partial V} Q d^3 \Bx R,
\end{equation}
where \( d^4 \Bx = I d^4 x \) is the pseudoscalar four-volume element associated with a parameterization of space time. For our purposes, we may assume that parameterization are standard basis coordinates associated with the basis \( \setlr{ \gamma_0, \gamma_1, \gamma_2, \gamma_3 } \). The surface differential form \( d^3 \Bx \) can be given specific meaning, but we do not actually care what that form is here, as all our surface integrals will be zero due to the boundary constraints of the variational principle.

Finally, we will utilize the fact that bivector products can be split into grade \(0,4\) and \( 2 \) components using anticommutator and commutator products, namely, given two bivectors \( F, G \), we have
\begin{equation}\label{eqn:maxwellLagrangian:1990}
\begin{aligned}
\gpgrade{ F G }{0,4} &= \inv{2} \lr{ F G + G F } \\
\gpgrade{ F G }{2} &= \inv{2} \lr{ F G – G F }.
\end{aligned}
\end{equation}

We may now proceed to evaluate the variation of the action for our presumed Lagrangian
\begin{equation}\label{eqn:maxwellLagrangian:2010}
S = \int d^4 x \lr{ \inv{2} F^2 – A \cdot J }.
\end{equation}
We seek solutions of the variational equation \( \delta S = 0 \), that are satisfied for all variations \( \delta A \), where the four-potential variations \( \delta A \) are zero on the boundaries of this action volume (i.e. an infinite spherical surface.)

We may start our variation in terms of \( F \) and \( A \)
\begin{equation}\label{eqn:maxwellLagrangian:1540}
\begin{aligned}
\delta S
&=
\int d^4 x \lr{ \inv{2} \lr{ \delta F } F + F \lr{ \delta F } } – \lr{ \delta A } \cdot J \\
&=
\int d^4 x \gpgrade{ \lr{ \delta F } F – \lr{ \delta A } J }{0,4} \\
&=
\int d^4 x \gpgrade{ \lr{ \grad \wedge \lr{\delta A} } F – \lr{ \delta A } J }{0,4} \\
&=
-\int d^4 x \gpgrade{ \lr{ \lr{\delta A} \lgrad } F – \lr{ \lr{ \delta A } \cdot \lgrad } F + \lr{ \delta A } J }{0,4} \\
&=
-\int d^4 x \gpgrade{ \lr{ \lr{\delta A} \lgrad } F + \lr{ \delta A } J }{0,4} \\
&=
-\int d^4 x \gpgrade{ \lr{\delta A} \lrgrad F – \lr{\delta A} \rgrad F + \lr{ \delta A } J }{0,4},
\end{aligned}
\end{equation}
where we have used arrows, when required, to indicate the directional action of the gradient.

Writing \( d^4 x = -I d^4 \Bx \), we have
\begin{equation}\label{eqn:maxwellLagrangian:1600}
\begin{aligned}
\delta S
&=
-\int_V d^4 x \gpgrade{ \lr{\delta A} \lrgrad F – \lr{\delta A} \rgrad F + \lr{ \delta A } J }{0,4} \\
&=
-\int_V \gpgrade{ -\lr{\delta A} I d^4 \Bx \lrgrad F – d^4 x \lr{\delta A} \rgrad F + d^4 x \lr{ \delta A } J }{0,4} \\
&=
\int_{\partial V} \gpgrade{ \lr{\delta A} I d^3 \Bx F }{0,4}
+ \int_V d^4 x \gpgrade{ \lr{\delta A} \lr{ \rgrad F – J } }{0,4}.
\end{aligned}
\end{equation}
The first integral is killed since \( \delta A = 0 \) on the boundary. The remaining integrand can be simplified to
\begin{equation}\label{eqn:maxwellLagrangian:1660}
\gpgrade{ \lr{\delta A} \lr{ \rgrad F – J } }{0,4} =
\gpgrade{ \lr{\delta A} \lr{ \grad F – J } }{0},
\end{equation}
where the grade-4 filter has also been discarded since \( \grad F = \grad \cdot F + \grad \wedge F = \grad \cdot F \) since \( \grad \wedge F = \grad \wedge \grad \wedge A = 0 \) by construction, which implies that the only non-zero grades in the multivector \( \grad F – J \) are vector grades. Also, the directional indicator on the gradient has been dropped, since there is no longer any ambiguity. We seek solutions of \( \gpgrade{ \lr{\delta A} \lr{ \grad F – J } }{0} = 0 \) for all variations \( \delta A \), namely
\begin{equation}\label{eqn:maxwellLagrangian:1620}
\boxed{
\grad F = J.
}
\end{equation}
This is Maxwell’s equation in it’s coordinate free STA form, found using the variational principle from a coordinate free multivector Maxwell Lagrangian, without having to resort to a coordinate expansion of that Lagrangian.

Lagrangian for fictitious magnetic sources.

The generalization of the Lagrangian to include magnetic charge and current densities can be as simple as utilizing two independent four-potential fields
\begin{equation}\label{eqn:maxwellLagrangian:n}
\LL = \inv{2} \lr{ \grad \wedge A }^2 – A \cdot J + \alpha \lr{ \inv{2} \lr{ \grad \wedge K }^2 – K \cdot M },
\end{equation}
where \( \alpha \) is an arbitrary multivector constant.

Variation of this Lagrangian provides two independent equations
\begin{equation}\label{eqn:maxwellLagrangian:1840}
\begin{aligned}
\grad \lr{ \grad \wedge A } &= J \\
\grad \lr{ \grad \wedge K } &= M.
\end{aligned}
\end{equation}
We may add these, scaling the second by \( -I \) (recall that \( I, \grad \) anticommute), to find
\begin{equation}\label{eqn:maxwellLagrangian:1860}
\grad \lr{ F_{\mathrm{e}} + I F_{\mathrm{m}} } = J – I M,
\end{equation}
which is \( \grad F = J – I M \), as desired.

It would be interesting to explore whether it is possible find Lagrangian that is dependent on a multivector potential, that would yield \( \grad F = J – I M \) directly, instead of requiring a superposition operation from the two independent solutions. One such possible potential is \( \tilde{A} = A – I K \), for which \( F = \gpgradetwo{ \grad \tilde{A} } = \grad \wedge A + I \lr{ \grad \wedge K } \). The author was not successful constructing such a Lagrangian.

Progressing towards coordinate free form of the Euler-Lagrange equations for Maxwell’s equation

June 17, 2022 math and physics play , , , , , , , , , ,

This is the 6th part of a series on finding Maxwell’s equations (including the fictitious magnetic sources that are useful in engineering) from a multivector Lagrangian representation.

[Click here for a PDF version of this series of posts, up to and including this one.]  The first, second, third, fourth, and fifth parts are also available here on this blog.

We managed to find Maxwell’s equation in it’s STA form by variation of a multivector Lagrangian, with respect to a four-vector field (the potential). That approach differed from the usual variation with respect to the coordinates of that four-vector, or the use of the Euler-Lagrange equations with respect to those coordinates.

Euler-Lagrange equations.

Having done so, an immediate question is whether we can express the Euler-Lagrange equations with respect to the four-potential in it’s entirety, instead of the coordinates of that vector. I have some intuition about how to completely avoid that use of coordinates, but first we can get part way there.

Consider a general Lagrangian, dependent on a field \( A \) and all it’s derivatives \( \partial_\mu A \)
\begin{equation}\label{eqn:fsquared:1180}
\LL = \LL( A, \partial_\mu A ).
\end{equation}

The variational principle requires
\begin{equation}\label{eqn:fsquared:1200}
0 = \delta S = \int d^4 x \delta \LL( A, \partial_\mu A ).
\end{equation}
That variation can be expressed as a limiting parametric operation as follows
\begin{equation}\label{eqn:fsquared:1220}
\delta S
= \int d^4 x
\lr{
\lim_{t \rightarrow 0} \ddt{} \LL( A + t \delta A )
+
\sum_\mu
\lim_{t \rightarrow 0} \ddt{} \LL( \partial_\mu A + t \delta \partial_\mu A )
}
\end{equation}
We eventually want a coordinate free expression for the variation, but we’ll use them to get there. We can expand the first derivative by chain rule as
\begin{equation}\label{eqn:fsquared:1240}
\begin{aligned}
\lim_{t \rightarrow 0} \ddt{} \LL( A + t \delta A )
&=
\lim_{t \rightarrow 0} \PD{(A^\alpha + t \delta A^\alpha)}{\LL} \PD{t}{}(A^\alpha + t \delta A^\alpha) \\
&=
\PD{A^\alpha}{\LL} \delta A^\alpha.
\end{aligned}
\end{equation}
This has the structure of a directional derivative \( A \). In particular, let
\begin{equation}\label{eqn:fsquared:1260}
\grad_A = \gamma^\alpha \PD{A^\alpha}{},
\end{equation}
so we have
\begin{equation}\label{eqn:fsquared:1280}
\lim_{t \rightarrow 0} \ddt{} \LL( A + t \delta A )
= \delta A \cdot \grad_A.
\end{equation}
Similarly,
\begin{equation}\label{eqn:fsquared:1300}
\lim_{t \rightarrow 0} \ddt{} \LL( \partial_\mu A + t \delta \partial_\mu A )
=
\PD{(\partial_\mu A^\alpha)}{\LL} \delta \partial_\mu A^\alpha,
\end{equation}
so we can define a gradient with respect to each of the derivatives of \(A \) as
\begin{equation}\label{eqn:fsquared:1320}
\grad_{\partial_\mu A} = \gamma^\alpha \PD{(\partial_\mu A^\alpha)}{}.
\end{equation}
Our variation can now be expressed in a somewhat coordinate free form
\begin{equation}\label{eqn:fsquared:1340}
\delta S = \int d^4 x \lr{
\lr{\delta A \cdot \grad_A} \LL + \lr{ \lr{\delta \partial_\mu A} \cdot \grad_{\partial_\mu A} } \LL
}.
\end{equation}
We now sum implicitly over pairs of indexes \( \mu \) (i.e. we are treating \( \grad_{\partial_\mu A} \) as an upper index entity). We can now proceed with our chain rule expansion
\begin{equation}\label{eqn:fsquared:1360}
\begin{aligned}
\delta S
&= \int d^4 x \lr{
\lr{\delta A \cdot \grad_A} \LL + \lr{ \lr{\delta \partial_\mu A} \cdot \grad_{\partial_\mu A} } \LL
} \\
&= \int d^4 x \lr{
\lr{\delta A \cdot \grad_A} \LL + \lr{ \lr{\partial_\mu \delta A} \cdot \grad_{\partial_\mu A} } \LL
} \\
&= \int d^4 x \lr{
\lr{\delta A \cdot \grad_A} \LL
+ \partial_\mu \lr{ \lr{ \delta A \cdot \grad_{\partial_\mu A} } \LL }
– \lr{\PD{x^\mu}{} \delta A \cdot \grad_{\partial_\mu A} \LL}_{\delta A}
}.
\end{aligned}
\end{equation}
As usual, we kill off the boundary term, by insisting that \( \delta A = 0 \) on the boundary, leaving us with a four-vector form of the field Euler-Lagrange equations
\begin{equation}\label{eqn:fsquared:1380}
\lr{\delta A \cdot \grad_A} \LL = \lr{\PD{x^\mu}{} \delta A \cdot \grad_{\partial_\mu A} \LL}_{\delta A},
\end{equation}
where the RHS derivatives are taken with \(\delta A \) held fixed. We seek solutions of this equation that hold for all variations \( \delta A \).

Application to the Maxwell Lagrangian.

For the Maxwell application we need a few helper calculations. The first, given a multivector \( B \), is
\begin{equation}\label{eqn:fsquared:1400}
\begin{aligned}
\lr{ \delta A \cdot \grad_A } A B
&=
\delta A^\alpha \PD{A^\alpha}{} \gamma_\beta A^\beta B \\
&=
\delta A^\alpha \gamma_\alpha B \\
&=
\lr{ \delta A } B.
\end{aligned}
\end{equation}

Now let’s compute, for multivector \( B \)
\begin{equation}\label{eqn:fsquared:1420}
\begin{aligned}
\lr{ \delta A \cdot \grad_{\partial_\mu A} } B F
&=
\delta A^\alpha \PD{(\partial_\mu A^\alpha)} B \lr{ \gamma^\beta \wedge \partial_\beta \lr{ \gamma_\pi A^\pi } } \\
&=
\delta A^\alpha B \lr{ \gamma^\mu \wedge \gamma_\alpha } \\
&=
B \lr{ \gamma^\mu \wedge \delta A }.
\end{aligned}
\end{equation}

Our Lagrangian is
\begin{equation}\label{eqn:fsquared:1440}
\LL = \inv{2} F^2 – \gpgrade{A \lr{ J – I M } }{0,4},
\end{equation}
so
\begin{equation}\label{eqn:fsquared:1460}
\lr{\delta A \cdot \grad_A} \LL
=
-\gpgrade{ \lr{ \delta A } \lr{ J – I M } }{0,4},
\end{equation}
and
\begin{equation}\label{eqn:fsquared:1480}
\begin{aligned}
\lr{ \delta A \cdot \grad_{\partial_\mu A} } \inv{2} F^2
&=
\inv{2} \lr{ F \lr{ \gamma^\mu \wedge \delta A } + \lr{ \gamma^\mu \wedge \delta A } F } \\
&=
\gpgrade{
\lr{ \gamma^\mu \wedge \delta A } F
}{0,4} \\
&=
-\gpgrade{
\lr{ \delta A \wedge \gamma^\mu } F
}{0,4} \\
&=
-\gpgrade{
\delta A \gamma^\mu F
–
\lr{ \delta A \cdot \gamma^\mu } F
}{0,4} \\
&=
-\gpgrade{
\delta A \gamma^\mu F
}{0,4}.
\end{aligned}
\end{equation}
Taking derivatives (holding \( \delta A \) fixed), we have
\begin{equation}\label{eqn:fsquared:1500}
\begin{aligned}
-\gpgrade{ \lr{ \delta A } \lr{ J – I M } }{0,4}
&=
-\gpgrade{
\delta A \partial_\mu \gamma^\mu F
}{0,4} \\
&=
-\gpgrade{
\delta A \grad F
}{0,4}.
\end{aligned}
\end{equation}
We’ve already seen that the solution can be expressed without grade selection as
\begin{equation}\label{eqn:fsquared:1520}
\grad F = \lr{ J – I M },
\end{equation}
which is Maxwell’s equation in it’s STA form. It’s not clear that this is really any less work, but it’s a step towards a coordinate free evaluation of the Maxwell Lagrangian (at least not having to use the coordinates \( A^\mu \) as we have to do in the tensor formalism.)

Gauge freedom and four-potentials in the STA form of Maxwell’s equation.

March 27, 2022 math and physics play , , , , , , , , , , , , , , , , , , , , ,

[If mathjax doesn’t display properly for you, click here for a PDF of this post]

Motivation.

In a recent video on the tensor structure of Maxwell’s equation, I made a little side trip down the road of potential solutions and gauge transformations. I thought that was worth writing up in text form.

The initial point of that side trip was just to point out that the Faraday tensor can be expressed in terms of four potential coordinates
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:20}
F_{\mu\nu} = \partial_\mu A_\nu – \partial_\nu A_\mu,
\end{equation}
but before I got there I tried to motivate this. In this post, I’ll outline the same ideas.

STA representation of Maxwell’s equation.

We’d gone through the work to show that Maxwell’s equation has the STA form
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:40}
\grad F = J.
\end{equation}
This is a deceptively compact representation, as it requires all of the following definitions
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:60}
\grad = \gamma^\mu \partial_\mu = \gamma_\mu \partial^\mu,
\end{equation}
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:80}
\partial_\mu = \PD{x^\mu}{},
\end{equation}
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:100}
\gamma^\mu \cdot \gamma_\nu = {\delta^\mu}_\nu,
\end{equation}
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:160}
\gamma_\mu \cdot \gamma_\nu = g_{\mu\nu},
\end{equation}
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:120}
\begin{aligned}
F
&= \BE + I c \BB \\
&= -E^k \gamma^k \gamma^0 – \inv{2} c B^r \gamma^s \gamma^t \epsilon^{r s t} \\
&= \inv{2} \gamma^{\mu} \wedge \gamma^{\nu} F_{\mu\nu},
\end{aligned}
\end{equation}
and
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:140}
\begin{aligned}
J &= \gamma_\mu J^\mu \\
J^\mu &= \frac{\rho}{\epsilon} \gamma_0 + \eta (\BJ \cdot \Be_k).
\end{aligned}
\end{equation}

Four-potentials in the STA representation.

In order to find the tensor form of Maxwell’s equation (starting from the STA representation), we first split the equation into two, since
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:180}
\grad F = \grad \cdot F + \grad \wedge F = J.
\end{equation}
The dot product is a four-vector, the wedge term is a trivector, and the current is a four-vector, so we have one grade-1 equation and one grade-3 equation
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:200}
\begin{aligned}
\grad \cdot F &= J \\
\grad \wedge F &= 0.
\end{aligned}
\end{equation}
The potential comes into the mix, since the curl equation above means that \( F \) necessarily can be written as the curl of some four-vector
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:220}
F = \grad \wedge A.
\end{equation}
One justification of this is that \( a \wedge (a \wedge b) = 0 \), for any vectors \( a, b \). Expanding such a double-curl out in coordinates is also worthwhile
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:240}
\begin{aligned}
\grad \wedge \lr{ \grad \wedge A }
&=
\lr{ \gamma_\mu \partial^\mu }
\wedge
\lr{ \gamma_\nu \partial^\nu }
\wedge
A \\
&=
\gamma^\mu \wedge \gamma^\nu \wedge \lr{ \partial_\mu \partial_\nu A }.
\end{aligned}
\end{equation}
Provided we have equality of mixed partials, this is a product of an antisymmetric factor and a symmetric factor, so the full sum is zero.

Things get interesting if one imposes a \( \grad \cdot A = \partial_\mu A^\mu = 0 \) constraint on the potential. If we do so, then
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:260}
\grad F = \grad^2 A = J.
\end{equation}
Observe that \( \grad^2 \) is the wave equation operator (often written as a square-box symbol.) That is
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:280}
\begin{aligned}
\grad^2
&= \partial^\mu \partial_\mu \\
&= \partial_0 \partial_0
– \partial_1 \partial_1
– \partial_2 \partial_2
– \partial_3 \partial_3 \\
&= \inv{c^2} \PDSq{t}{} – \spacegrad^2.
\end{aligned}
\end{equation}
This is also an operator for which the Green’s function is well known ([1]), which means that we can immediately write the solutions
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:300}
A(x) = \int G(x,x’) J(x’) d^4 x’.
\end{equation}
However, we have no a-priori guarantee that such a solution has zero divergence. We can fix that by making a gauge transformation of the form
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:320}
A \rightarrow A – \grad \chi.
\end{equation}
Observe that such a transformation does not change the electromagnetic field
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:340}
F = \grad \wedge A \rightarrow \grad \wedge \lr{ A – \grad \chi },
\end{equation}
since
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:360}
\grad \wedge \grad \chi = 0,
\end{equation}
(also by equality of mixed partials.) Suppose that \( \tilde{A} \) is a solution of \( \grad^2 \tilde{A} = J \), and \( \tilde{A} = A + \grad \chi \), where \( A \) is a zero divergence field to be determined, then
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:380}
\grad \cdot \tilde{A}
=
\grad \cdot A + \grad^2 \chi,
\end{equation}
or
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:400}
\grad^2 \chi = \grad \cdot \tilde{A}.
\end{equation}
So if \( \tilde{A} \) does not have zero divergence, we can find a \( \chi \)
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:420}
\chi(x) = \int G(x,x’) \grad’ \cdot \tilde{A}(x’) d^4 x’,
\end{equation}
so that \( A = \tilde{A} – \grad \chi \) does have zero divergence.

References

[1] JD Jackson. Classical Electrodynamics. John Wiley and Sons, 2nd edition, 1975.

Curvilinear coordinates and gradient in spacetime, and reciprocal frames.

December 1, 2020 math and physics play , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,

[If mathjax doesn’t display properly for you, click here for a PDF of this post]

Motivation.

I started pondering some aspects of spacetime integration theory, and found that there were some aspects of the concepts of reciprocal frames that were not clear to me. In the process of sorting those ideas out for myself, I wrote up the following notes.

In the notes below, I will introduce the many of the prerequisite ideas that are needed to express and apply the fundamental theorem of geometric calculus in a 4D relativistic context. The focus will be the Dirac’s algebra of special relativity, known as STA (Space Time Algebra) in geometric algebra parlance. If desired, it should be clear how to apply these ideas to lower or higher dimensional spaces, and to plain old Euclidean metrics.

On notation.

In Euclidean space we use bold face reciprocal frame vectors \( \Bx^i \cdot \Bx_j = {\delta^i}_j \), which nicely distinguishes them from the generalized coordinates \( x_i, x^j \) associated with the basis or the reciprocal frame, that is
\begin{equation}\label{eqn:reciprocalblog:640}
\Bx = x^i \Bx_i = x_j \Bx^j.
\end{equation}
On the other hand, it is conventional to use non-bold face for both the four-vectors and their coordinates in STA, such as the following standard basis decomposition
\begin{equation}\label{eqn:reciprocalblog:660}
x = x^\mu \gamma_\mu = x_\mu \gamma^\mu.
\end{equation}
If we use non-bold face \( x^\mu, x_\nu \) for the coordinates with respect to a specified frame, then we cannot also use non-bold face for the curvilinear basis vectors.

To resolve this notational ambiguity, I’ve chosen to use bold face \( \Bx^\mu, \Bx_\nu \) symbols as the curvilinear basis elements in this relativistic context, as we do for Euclidean spaces.

Basis and coordinates.

Definition 1.1: Standard Dirac basis.

The Dirac basis elements are \(\setlr{ \gamma_0, \gamma_1, \gamma_2, \gamma_3 } \), satisfying
\begin{equation}\label{eqn:reciprocalblog:1940}
\gamma_0^2 = 1 = -\gamma_k^2, \quad \forall k = 1,2,3,
\end{equation}
and
\begin{equation}\label{eqn:reciprocalblog:740}
\gamma_\mu \cdot \gamma_\nu = 0, \quad \forall \mu \ne \nu.
\end{equation}

A conventional way of summarizing these orthogonality relationships is \( \gamma_\mu \cdot \gamma_\nu = \eta_{\mu\nu} \), where \( \eta_{\mu\nu} \) are the elements of the metric \( G = \text{diag}(+,-,-,-) \).

Definition 1.2: Reciprocal basis for the standard Dirac basis.

We define a reciprocal basis \( \setlr{ \gamma^0, \gamma^1, \gamma^2, \gamma^3} \) satisfying \( \gamma^\mu \cdot \gamma_\nu = {\delta^\mu}_\nu, \forall \mu,\nu \in 0,1,2,3 \).

Theorem 1.1: Reciprocal basis uniqueness.

This reciprocal basis is unique, and for our choice of metric has the values
\begin{equation}\label{eqn:reciprocalblog:1960}
\gamma^0 = \gamma_0, \quad \gamma^k = -\gamma_k, \quad \forall k = 1,2,3.
\end{equation}

Proof is left to the reader.

Definition 1.3: Coordinates.

We define the coordinates of a vector with respect to the standard basis as \( x^\mu \) satisfying
\begin{equation}\label{eqn:reciprocalblog:1980}
x = x^\mu \gamma_\mu,
\end{equation}
and define the coordinates of a vector with respect to the reciprocal basis as \( x_\mu \) satisfying
\begin{equation}\label{eqn:reciprocalblog:2000}
x = x_\mu \gamma^\mu,
\end{equation}

Theorem 1.2: Coordinates.

Given the definitions above, we may compute the coordinates of a vector, simply by dotting with the basis elements
\begin{equation}\label{eqn:reciprocalblog:2020}
x^\mu = x \cdot \gamma^\mu,
\end{equation}
and
\begin{equation}\label{eqn:reciprocalblog:2040}
x_\mu = x \cdot \gamma_\mu,
\end{equation}

Start proof:

This follows by straightforward computation
\begin{equation}\label{eqn:reciprocalblog:840}
\begin{aligned}
x \cdot \gamma^\mu
&=
\lr{ x^\nu \gamma_\nu } \cdot \gamma^\mu \\
&=
x^\nu \lr{ \gamma_\nu \cdot \gamma^\mu } \\
&=
x^\nu {\delta_\nu}^\mu \\
&=
x^\mu,
\end{aligned}
\end{equation}
and
\begin{equation}\label{eqn:reciprocalblog:860}
\begin{aligned}
x \cdot \gamma_\mu
&=
\lr{ x_\nu \gamma^\nu } \cdot \gamma_\mu \\
&=
x_\nu \lr{ \gamma^\nu \cdot \gamma_\mu } \\
&=
x_\nu {\delta^\nu}_\mu \\
&=
x_\mu.
\end{aligned}
\end{equation}

End proof.

Derivative operators.

We’d like to determine the form of the (spacetime) gradient operator. The gradient can be defined in terms of coordinates directly, but we choose an implicit definition, in terms of the directional derivative.

Definition 1.4: Directional derivative and gradient.

Let \( F = F(x) \) be a four-vector parameterized multivector. The directional derivative of \( F \) with respect to the (four-vector) direction \( a \) is denoted
\begin{equation}\label{eqn:reciprocalblog:2060}
\lr{ a \cdot \grad } F = \lim_{\epsilon \rightarrow 0} \frac{ F(x + \epsilon a) – F(x) }{ \epsilon },
\end{equation}
where \( \grad \) is called the space time gradient.

Theorem 1.3: Gradient.

The standard basis representation of the gradient is
\begin{equation}\label{eqn:reciprocalblog:2080}
\grad = \gamma^\mu \partial_\mu,
\end{equation}
where
\begin{equation}\label{eqn:reciprocalblog:2100}
\partial_\mu = \PD{x^\mu}{}.
\end{equation}

Start proof:

The Dirac gradient pops naturally out of the coordinate representation of the directional derivative, as we can see by expanding \( F(x + \epsilon a) \) in Taylor series
\begin{equation}\label{eqn:reciprocalblog:900}
\begin{aligned}
F(x + \epsilon a)
&= F(x) + \epsilon \frac{dF(x + \epsilon a)}{d\epsilon} + O(\epsilon^2) \\
&= F(x) + \epsilon \PD{\lr{x^\mu + \epsilon a^\mu}}{F} \PD{\epsilon}{\lr{x^\mu + \epsilon a^\mu}} \\
&= F(x) + \epsilon \PD{\lr{x^\mu + \epsilon a^\mu}}{F} a^\mu.
\end{aligned}
\end{equation}
The directional derivative is
\begin{equation}\label{eqn:reciprocalblog:920}
\begin{aligned}
\lim_{\epsilon \rightarrow 0}
\frac{F(x + \epsilon a) – F(x)}{\epsilon}
&=
\lim_{\epsilon \rightarrow 0}\,
a^\mu
\PD{\lr{x^\mu + \epsilon a^\mu}}{F} \\
&=
a^\mu
\PD{x^\mu}{F} \\
&=
\lr{a^\nu \gamma_\nu} \cdot \gamma^\mu \PD{x^\mu}{F} \\
&=
a \cdot \lr{ \gamma^\mu \partial_\mu } F.
\end{aligned}
\end{equation}

End proof.

Curvilinear bases.

Curvilinear bases are the foundation of the fundamental theorem of multivector calculus. This form of integral calculus is defined over parameterized surfaces (called manifolds) that satisfy some specific non-degeneracy and continuity requirements.

A parameterized vector \( x(u,v, \cdots w) \) can be thought of as tracing out a hypersurface (curve, surface, volume, …), where the dimension of the hypersurface depends on the number of parameters. At each point, a bases can be constructed from the differentials of the parameterized vector. Such a basis is called the tangent space to the surface at the point in question. Our curvilinear bases will be related to these differentials. We will also be interested in a dual basis that is restricted to the span of the tangent space. This dual basis will be called the reciprocal frame, and line the basis of the tangent space itself, also varies from point to point on the surface.

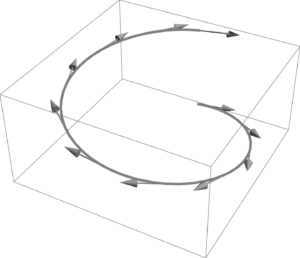
Fig 1a. One parameter curve, with illustration of tangent space along the curve.

Fig 1b. Two parameter surface, with illustration of tangent space along the surface.

One and two parameter spaces are illustrated in fig. 1a, and 1b.  The tangent space basis at a specific point of a two parameter surface, \( x(u^0, u^1) \), is illustrated in fig. 1. The differential directions that span the tangent space are
\begin{equation}\label{eqn:reciprocalblog:1040}
\begin{aligned}
d\Bx_0 &= \PD{u^0}{x} du^0 \\
d\Bx_1 &= \PD{u^1}{x} du^1,
\end{aligned}
\end{equation}
and the tangent space itself is \( \mbox{Span}\setlr{ d\Bx_0, d\Bx_1 } \). We may form an oriented surface area element \( d\Bx_0 \wedge d\Bx_1 \) over this surface.

Fig 2. Two parameter surface.

Tangent spaces associated with 3 or more parameters cannot be easily visualized in three dimensions, but the idea generalizes algebraically without trouble.

Definition 1.5: Tangent basis and space.

Given a parameterization \( x = x(u^0, \cdots, u^N) \), where \( N < 4 \), the span of the vectors
\begin{equation}\label{eqn:reciprocalblog:2120}
\Bx_\mu = \PD{u^\mu}{x},
\end{equation}
is called the tangent space for the hypersurface associated with the parameterization, and it’s basis is
\( \setlr{ \Bx_\mu } \).

Later we will see that parameterization constraints must be imposed, as not all surfaces generated by a set of parameterizations are useful for integration theory. In particular, degenerate parameterizations for which the wedge products of the tangent space basis vectors are zero, or those wedge products cannot be inverted, are not physically meaningful. Properly behaved surfaces of this sort are called manifolds.

Having introduced curvilinear coordinates associated with a parameterization, we can now determine the form of the gradient with respect to a parameterization of spacetime.

Theorem 1.4: Gradient, curvilinear representation.

Given a spacetime parameterization \( x = x(u^0, u^1, u^2, u^3) \), the gradient with respect to the parameters \( u^\mu \) is
\begin{equation}\label{eqn:reciprocalblog:2140}
\grad = \sum_\mu \Bx^\mu
\PD{u^\mu}{},
\end{equation}
where
\begin{equation}\label{eqn:reciprocalblog:2160}
\Bx^\mu = \grad u^\mu.
\end{equation}
The vectors \( \Bx^\mu \) are called the reciprocal frame vectors, and the ordered set \( \setlr{ \Bx^0, \Bx^1, \Bx^2, \Bx^3 } \) is called the reciprocal basis.It is convenient to define \( \partial_\mu \equiv \PDi{u^\mu}{} \), so that the gradient can be expressed in mixed index representation
\begin{equation}\label{eqn:reciprocalblog:2180}
\grad = \Bx^\mu \partial_\mu.
\end{equation}
This introduces some notational ambiguity, since we used \( \partial_\mu = \PDi{x^\mu}{} \) for the standard basis derivative operators too, but we will be careful to be explicit when there is any doubt about what is intended.

Start proof:

The proof follows by application of the chain rule.
\begin{equation}\label{eqn:reciprocalblog:960}
\begin{aligned}
\grad F
&=
\gamma^\alpha \PD{x^\alpha}{F} \\
&=
\gamma^\alpha
\PD{x^\alpha}{u^\mu}
\PD{u^\mu}{F} \\
&=
\lr{ \grad u^\mu } \PD{u^\mu}{F} \\
&=
\Bx^\mu \PD{u^\mu}{F}.
\end{aligned}
\end{equation}

End proof.

Theorem 1.5: Reciprocal relationship.

The vectors \( \Bx^\mu = \grad u^\mu \), and \( \Bx_\mu = \PDi{u^\mu}{x} \) satisfy the reciprocal relationship
\begin{equation}\label{eqn:reciprocalblog:2200}
\Bx^\mu \cdot \Bx_\nu = {\delta^\mu}_\nu.
\end{equation}

Start proof:

\begin{equation}\label{eqn:reciprocalblog:1020}
\begin{aligned}
\Bx^\mu \cdot \Bx_\nu
&=
\grad u^\mu \cdot
\PD{u^\nu}{x} \\
&=
\lr{
\gamma^\alpha \PD{x^\alpha}{u^\mu}
}
\cdot
\lr{
\PD{u^\nu}{x^\beta} \gamma_\beta
} \\
&=
{\delta^\alpha}_\beta \PD{x^\alpha}{u^\mu}
\PD{u^\nu}{x^\beta} \\
&=
\PD{x^\alpha}{u^\mu} \PD{u^\nu}{x^\alpha} \\
&=
\PD{u^\nu}{u^\mu} \\
&=
{\delta^\mu}_\nu
.
\end{aligned}
\end{equation}

End proof.

It is instructive to consider an example. Here is a parameterization that scales the proper time parameter, and uses polar coordinates in the \(x-y\) plane.

Problem: Compute the curvilinear and reciprocal basis.

Given
\begin{equation}\label{eqn:reciprocalblog:2360}
x(t,\rho,\theta,z) = c t \gamma_0 + \gamma_1 \rho e^{i \theta} + z \gamma_3,
\end{equation}
where \( i = \gamma_1 \gamma_2 \), compute the curvilinear frame vectors and their reciprocals.

Answer

The frame vectors are all easy to compute
\begin{equation}\label{eqn:reciprocalblog:1180}
\begin{aligned}
\Bx_0 &= \PD{t}{x} = c \gamma_0 \\
\Bx_1 &= \PD{\rho}{x} = \gamma_1 e^{i \theta} \\
\Bx_2 &= \PD{\theta}{x} = \rho \gamma_1 \gamma_1 \gamma_2 e^{i \theta} = – \rho \gamma_2 e^{i \theta} \\
\Bx_3 &= \PD{z}{x} = \gamma_3.
\end{aligned}
\end{equation}
The \( \Bx_1 \) vector is radial, \( \Bx^2 \) is perpendicular to that tangent to the same unit circle, as plotted in fig 3.

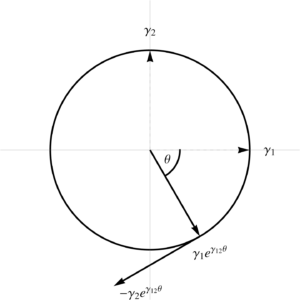
Fig3: Tangent space direction vectors.

All of these particular frame vectors happen to be mutually perpendicular, something that will not generally be true for a more arbitrary parameterization.

To compute the reciprocal frame vectors, we must express our parameters in terms of \( x^\mu \) coordinates, and use implicit integration techniques to deal with the coupling of the rotational terms. First observe that
\begin{equation}\label{eqn:reciprocalblog:1200}
\gamma_1 e^{i\theta}
= \gamma_1 \lr{ \cos\theta + \gamma_1 \gamma_2 \sin\theta }
= \gamma_1 \cos\theta – \gamma_2 \sin\theta,
\end{equation}
so
\begin{equation}\label{eqn:reciprocalblog:1220}
\begin{aligned}
x^0 &= c t \\
x^1 &= \rho \cos\theta \\
x^2 &= -\rho \sin\theta \\
x^3 &= z.
\end{aligned}
\end{equation}
We can easily evaluate the \( t, z \) gradients
\begin{equation}\label{eqn:reciprocalblog:1240}
\begin{aligned}
\grad t &= \frac{\gamma^1 }{c} \\
\grad z &= \gamma^3,
\end{aligned}
\end{equation}
but the \( \rho, \theta \) gradients are not as easy. First writing
\begin{equation}\label{eqn:reciprocalblog:1260}
\rho^2 = \lr{x^1}^2 + \lr{x^2}^2,
\end{equation}
we find
\begin{equation}\label{eqn:reciprocalblog:1280}
\begin{aligned}
2 \rho \grad \rho = 2 \lr{ x^1 \grad x^1 + x^2 \grad x^2 }
&= 2 \rho \lr{ \cos\theta \gamma^1 – \sin\theta \gamma^2 } \\
&= 2 \rho \gamma^1 \lr{ \cos\theta – \gamma_1 \gamma^2 \sin\theta } \\
&= 2 \rho \gamma^1 e^{i\theta},
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:reciprocalblog:1300}
\grad \rho = \gamma^1 e^{i\theta}.
\end{equation}
For the \( \theta \) gradient, we can write
\begin{equation}\label{eqn:reciprocalblog:1320}
\tan\theta = -\frac{x^2}{x^1},
\end{equation}
so
\begin{equation}\label{eqn:reciprocalblog:1340}
\begin{aligned}
\inv{\cos^2 \theta} \grad \theta
&= -\frac{\gamma^2}{x^1} – x^2 \frac{-\gamma^1}{\lr{x^1}^2} \\
&= \inv{\lr{x^1}^2} \lr{ – \gamma^2 x^1 + \gamma^1 x^2 } \\
&= \frac{\rho}{\rho^2 \cos^2\theta } \lr{ – \gamma^2 \cos\theta – \gamma^1 \sin\theta } \\
&= -\frac{1}{\rho \cos^2\theta } \gamma^2 \lr{ \cos\theta + \gamma_2 \gamma^1 \sin\theta } \\
&= -\frac{\gamma^2 e^{i\theta} }{\rho \cos^2\theta },
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:reciprocalblog:1360}
\grad\theta = -\inv{\rho} \gamma^2 e^{i\theta}.
\end{equation}
In summary,
\begin{equation}\label{eqn:reciprocalblog:1380}
\begin{aligned}
\Bx^0 &= \frac{\gamma^0}{c} \\
\Bx^1 &= \gamma^1 e^{i\theta} \\
\Bx^2 &= -\inv{\rho} \gamma^2 e^{i\theta} \\
\Bx^3 &= \gamma^3.
\end{aligned}
\end{equation}

Despite being a fairly simple parameterization, it was still fairly difficult to solve for the gradients when the parameterization introduced coupling between the coordinates. In this particular case, we could have solved for the parameters in terms of the coordinates (but it was easier not to), but that will not generally be true. We want a less labor intensive strategy to find the reciprocal frame. When we have a full parameterization of spacetime, then we can do this with nothing more than a matrix inversion.

Theorem 1.6: Reciprocal frame matrix equations.

Given a spacetime basis \( \setlr{\Bx_0, \cdots \Bx_3} \), let \( [\Bx_\mu] \) and \( [\Bx^\nu] \) be column matrices with the coordinates of these vectors and their reciprocals, with respect to the standard basis \( \setlr{\gamma_0, \gamma_1, \gamma_2, \gamma_3 } \). Let
\begin{equation}\label{eqn:reciprocalblog:2220}
A =
\begin{bmatrix}
[\Bx_0] & \cdots & [\Bx_{3}]
\end{bmatrix}
,\qquad
X =
\begin{bmatrix}
[\Bx^0] & \cdots & [\Bx^{3}]
\end{bmatrix}.
\end{equation}
The coordinates of the reciprocal frame vectors can be found by solving
\begin{equation}\label{eqn:reciprocalblog:2240}
A^\T G X = 1,
\end{equation}
where \( G = \text{diag}(1,-1,-1,-1) \) and the RHS is an \( 4 \times 4 \) identity matrix.

Start proof:

Let \( \Bx_\mu = {a_\mu}^\alpha \gamma_\alpha, \Bx^\nu = b^{\nu\beta} \gamma_\beta \), so that
\begin{equation}\label{eqn:reciprocalblog:140}
A =
\begin{bmatrix}
{a_\nu}^\mu
\end{bmatrix},
\end{equation}
and
\begin{equation}\label{eqn:reciprocalblog:160}
X =
\begin{bmatrix}
b^{\nu\mu}
\end{bmatrix},
\end{equation}
where \( \mu \in [0,3]\) are the row indexes and \( \nu \in [0,N-1]\) are the column indexes. The reciprocal frame satisfies \( \Bx_\mu \cdot \Bx^\nu = {\delta_\mu}^\nu \), which has the coordinate representation of
\begin{equation}\label{eqn:reciprocalblog:180}
\begin{aligned}
\Bx_\mu \cdot \Bx^\nu
&=
\lr{
{a_\mu}^\alpha \gamma_\alpha
}
\cdot
\lr{
b^{\nu\beta} \gamma_\beta
} \\
&=
{a_\mu}^\alpha
\eta_{\alpha\beta}
b^{\nu\beta} \\
&=
{[A^\T G B]_\mu}^\nu,
\end{aligned}
\end{equation}
where \( \mu \) is the row index and \( \nu \) is the column index.

End proof.

Problem: Matrix inversion reciprocals.

For the parameterization of \ref{eqn:reciprocalblog:2360}, find the reciprocal frame vectors by matrix inversion.

Answer

We expanded \( \Bx_1 \) explicitly in \ref{eqn:reciprocalblog:1200}. Doing the same for \( \Bx_2 \), we have
\begin{equation}\label{eqn:reciprocalblog:1201}
\Bx_2 =
-\rho \gamma_2 e^{i\theta}
= -\rho \gamma_2 \lr{ \cos\theta + \gamma_1 \gamma_2 \sin\theta }
= – \rho \lr{ \gamma_2 \cos\theta + \gamma_1 \sin\theta}.
\end{equation}
Reading off the coordinates of our frame vectors, we have
\begin{equation}\label{eqn:reciprocalblog:1400}
X =
\begin{bmatrix}
c & 0 & 0 & 0 \\
0 & C & -\rho S & 0 \\
0 & -S & -\rho C & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix},
\end{equation}
where \( C = \cos\theta \) and \( S = \sin\theta \). We want
\begin{equation}\label{eqn:reciprocalblog:1420}
Y =
{\begin{bmatrix}
c & 0 & 0 & 0 \\
0 & -C & S & 0 \\
0 & \rho S & \rho C & 0 \\
0 & 0 & 0 & -1 \\
\end{bmatrix}}^{-1}
=
\begin{bmatrix}
\inv{c} & 0 & 0 & 0 \\
0 & -C & \frac{S}{\rho} & 0 \\
0 & S & \frac{C}{\rho} & 0 \\
0 & 0 & 0 & -1 \\
\end{bmatrix}.
\end{equation}
We can read off the coordinates of the reciprocal frame vectors
\begin{equation}\label{eqn:reciprocalblog:1440}
\begin{aligned}
\Bx^0 &= \inv{c} \gamma_0 \\
\Bx^1 &= -\cos\theta \gamma_1 + \sin\theta \gamma_2 \\
\Bx^2 &= \inv{\rho} \lr{ \sin\theta \gamma_1 + \cos\theta \gamma_2 } \\
\Bx^3 &= -\gamma_3.
\end{aligned}
\end{equation}
Factoring out \( \gamma^1 \) from the \( \Bx^1 \) terms, we find
\begin{equation}\label{eqn:reciprocalblog:1460}
\begin{aligned}
\Bx^1
&= -\cos\theta \gamma_1 + \sin\theta \gamma_2 \\
&= \gamma^1 \lr{ \cos\theta + \gamma_1 \gamma_2 \sin\theta } \\
&= \gamma^1 e^{i\theta}.
\end{aligned}
\end{equation}
Similarly for \( \Bx^2 \),
\begin{equation}\label{eqn:reciprocalblog:1480}
\begin{aligned}
\Bx^2
&= \inv{\rho} \lr{ \sin\theta \gamma_1 + \cos\theta \gamma_2 } \\
&= \frac{\gamma^2}{\rho} \lr{ \sin\theta \gamma_2 \gamma_1 – \cos\theta } \\
&= -\frac{\gamma^2}{\rho} e^{i\theta}.
\end{aligned}
\end{equation}
This matches \ref{eqn:reciprocalblog:1380}, as expected, but required only algebraic work to compute.

There will be circumstances where we parameterize only a subset of spacetime, and are interested in calculating quantities associated with such a surface. For example, suppose that
\begin{equation}\label{eqn:reciprocalblog:1500}
x(\rho,\theta) = \gamma_1 \rho e^{i \theta},
\end{equation}
where \( i = \gamma_1 \gamma_2 \) as before. We are now parameterizing only the \(x-y\) plane. We will still find
\begin{equation}\label{eqn:reciprocalblog:1520}
\begin{aligned}
\Bx_1 &= \gamma_1 e^{i \theta} \\
\Bx_2 &= -\gamma_2 \rho e^{i \theta}.
\end{aligned}
\end{equation}
We can compute the reciprocals of these vectors using the gradient method. It’s possible to state matrix equations representing the reciprocal relationship of \ref{eqn:reciprocalblog:2200}, which, in this case, is \( X^\T G Y = 1 \), where the RHS is a \( 2 \times 2 \) identity matrix, and \( X, Y\) are \( 4\times 2\) matrices of coordinates, with
\begin{equation}\label{eqn:reciprocalblog:1540}
X =
\begin{bmatrix}
0 & 0 \\
C & -\rho S \\
-S & -\rho C \\
0 & 0
\end{bmatrix}.
\end{equation}
We no longer have a square matrix problem to solve, and our solution set is multivalued. In particular, this matrix equation has solutions
\begin{equation}\label{eqn:reciprocalblog:1560}
\begin{aligned}
\Bx^1 &= \gamma^1 e^{i\theta} + \alpha \gamma^0 + \beta \gamma^3 \\
\Bx^2 &= -\frac{\gamma^2}{\rho} e^{i\theta} + \alpha’ \gamma^0 + \beta’ \gamma^3.
\end{aligned}
\end{equation}
where \( \alpha, \alpha’, \beta, \beta’ \) are arbitrary constants. In the example we considered, we saw that our \( \rho, \theta \) parameters were functions of only \( x^1, x^2 \), so taking gradients could not introduce any \( \gamma^0, \gamma^3 \) dependence in \( \Bx^1, \Bx^2 \). It seems reasonable to assert that we seek an algebraic method of computing a set of vectors that satisfies the reciprocal relationships, where that set of vectors is restricted to the tangent space. We will need to figure out how to prove that this reciprocal construction is identical to the parameter gradients, but let’s start with figuring out what such a tangent space restricted solution looks like.

Theorem 1.7: Reciprocal frame for two parameter subspace.

Given two vectors, \( \Bx_1, \Bx_2 \), the vectors \( \Bx^1, \Bx^2 \in \mbox{Span}\setlr{ \Bx_1, \Bx_2 } \) such that \( \Bx^\mu \cdot \Bx_\nu = {\delta^\mu}_\nu \) are given by
\begin{equation}\label{eqn:reciprocalblog:2260}
\begin{aligned}
\Bx^1 &= \Bx_2 \cdot \inv{\Bx_1 \wedge \Bx_2} \\
\Bx^2 &= -\Bx_1 \cdot \inv{\Bx_1 \wedge \Bx_2},
\end{aligned}
\end{equation}
provided \( \Bx_1 \wedge \Bx_2 \ne 0 \) and
\( \lr{ \Bx_1 \wedge \Bx_2 }^2 \ne 0 \).

Start proof:

The most general set of vectors that satisfy the span constraint are
\begin{equation}\label{eqn:reciprocalblog:1580}
\begin{aligned}
\Bx^1 &= a \Bx_1 + b \Bx_2 \\
\Bx^2 &= c \Bx_1 + d \Bx_2.
\end{aligned}
\end{equation}
We can use wedge products with either \( \Bx_1 \) or \( \Bx_2 \) to eliminate the other from the RHS
\begin{equation}\label{eqn:reciprocalblog:1600}
\begin{aligned}
\Bx^1 \wedge \Bx_2 &= a \lr{ \Bx_1 \wedge \Bx_2 } \\
\Bx^1 \wedge \Bx_1 &= – b \lr{ \Bx_1 \wedge \Bx_2 } \\
\Bx^2 \wedge \Bx_2 &= c \lr{ \Bx_1 \wedge \Bx_2 } \\
\Bx^2 \wedge \Bx_1 &= – d \lr{ \Bx_1 \wedge \Bx_2 },
\end{aligned}
\end{equation}
and then dot both sides with \( \Bx_1 \wedge \Bx_2 \) to produce four scalar equations
\begin{equation}\label{eqn:reciprocalblog:1640}
\begin{aligned}
a \lr{ \Bx_1 \wedge \Bx_2 }^2
&= \lr{ \Bx^1 \wedge \Bx_2 } \cdot \lr{ \Bx_1 \wedge \Bx_2 } \\
&=
\lr{ \Bx_2 \cdot \Bx_1 } \lr{ \Bx^1 \cdot \Bx_2 }
–
\lr{ \Bx_2 \cdot \Bx_2 } \lr{ \Bx^1 \cdot \Bx_1 } \\
&=
\lr{ \Bx_2 \cdot \Bx_1 } (0)
–
\lr{ \Bx_2 \cdot \Bx_2 } (1) \\
&= – \Bx_2 \cdot \Bx_2
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:reciprocalblog:1660}
\begin{aligned}
– b \lr{ \Bx_1 \wedge \Bx_2 }^2
&=
\lr{ \Bx^1 \wedge \Bx_1 } \cdot \lr{ \Bx_1 \wedge \Bx_2 } \\
&=
\lr{ \Bx^1 \cdot \Bx_2 } \lr{ \Bx_1 \cdot \Bx_1 }
–
\lr{ \Bx^1 \cdot \Bx_1 } \lr{ \Bx_1 \cdot \Bx_2 } \\
&=
(0) \lr{ \Bx_1 \cdot \Bx_1 }
–
(1) \lr{ \Bx_1 \cdot \Bx_2 } \\
&= – \Bx_1 \cdot \Bx_2
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:reciprocalblog:1680}
\begin{aligned}
c \lr{ \Bx_1 \wedge \Bx_2 }^2
&= \lr{ \Bx^2 \wedge \Bx_2 } \cdot \lr{ \Bx_1 \wedge \Bx_2 } \\
&=
\lr{ \Bx_2 \cdot \Bx_1 } \lr{ \Bx^2 \cdot \Bx_2 }
–
\lr{ \Bx_2 \cdot \Bx_2 } \lr{ \Bx^2 \cdot \Bx_1 } \\
&=
\lr{ \Bx_2 \cdot \Bx_1 } (1)
–
\lr{ \Bx_2 \cdot \Bx_2 } (0) \\
&= \Bx_2 \cdot \Bx_1
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:reciprocalblog:1700}
\begin{aligned}
– d \lr{ \Bx_1 \wedge \Bx_2 }^2
&= \lr{ \Bx^2 \wedge \Bx_1 } \cdot \lr{ \Bx_1 \wedge \Bx_2 } \\
&=
\lr{ \Bx_1 \cdot \Bx_1 } \lr{ \Bx^2 \cdot \Bx_2 }
–
\lr{ \Bx_1 \cdot \Bx_2 } \lr{ \Bx^2 \cdot \Bx_1 } \\
&=
\lr{ \Bx_1 \cdot \Bx_1 } (1)
–
\lr{ \Bx_1 \cdot \Bx_2 } (0) \\
&= \Bx_1 \cdot \Bx_1.
\end{aligned}
\end{equation}
Putting the pieces together we have
\begin{equation}\label{eqn:reciprocalblog:1740}
\begin{aligned}
\Bx^1
&= \frac{ – \lr{ \Bx_2 \cdot \Bx_2 } \Bx_1 + \lr{ \Bx_1 \cdot \Bx_2 } \Bx_2
}{\lr{\Bx_1 \wedge \Bx_2}^2} \\
&=
\frac{
\Bx_2 \cdot \lr{ \Bx_1 \wedge \Bx_2 }
}{\lr{\Bx_1 \wedge \Bx_2}^2} \\
&=
\Bx_2 \cdot \inv{\Bx_1 \wedge \Bx_2}
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:reciprocalblog:1760}
\begin{aligned}
\Bx^2
&=
\frac{ \lr{ \Bx_1 \cdot \Bx_2 } \Bx_1 – \lr{ \Bx_1 \cdot \Bx_1 } \Bx_2
}{\lr{\Bx_1 \wedge \Bx_2}^2} \\
&=
\frac{ -\Bx_1 \cdot \lr{ \Bx_1 \wedge \Bx_2 } }
{\lr{\Bx_1 \wedge \Bx_2}^2} \\
&=
-\Bx_1 \cdot \inv{\Bx_1 \wedge \Bx_2}
\end{aligned}
\end{equation}

End proof.

Lemma 1.1: Distribution identity.

Given k-vectors \( B, C \) and a vector \( a \), where the grade of \( C \) is greater than that of \( B \), then
\begin{equation}\label{eqn:reciprocalblog:2280}
\lr{a \wedge B} \cdot C = a \cdot \lr{ B \cdot C }.
\end{equation}

See [1] for a proof.

Theorem 1.8: Higher order tangent space reciprocals.

Given an \(N\) parameter tangent space with basis \( \setlr{ \Bx_0, \Bx_1, \cdots \Bx_{N-1} } \), the reciprocals are given by
\begin{equation}\label{eqn:reciprocalblog:2300}
\Bx^\mu = (-1)^\mu
\lr{ \Bx_0 \wedge \cdots \check{\Bx_\mu} \cdots \wedge \Bx_{N-1} } \cdot I_N^{-1},
\end{equation}
where the checked term (\(\check{\Bx_\mu}\)) indicates that all terms are included in the wedges except the \( \Bx_\mu \) term, and \( I_N = \Bx_0 \wedge \cdots \Bx_{N-1} \) is the pseudoscalar for the tangent space.

Start proof:

I’ll outline the proof for the three parameter tangent space case, from which the pattern will be clear. The motivation for this proof is a reexamination of the algebraic structure of the two vector solution. Suppose we have a tangent space basis \( \setlr{\Bx_0, \Bx_1} \), for which we’ve shown that
\begin{equation}\label{eqn:reciprocalblog:1860}
\begin{aligned}
\Bx^0
&= \Bx_1 \cdot \inv{\Bx_0 \wedge \Bx_1} \\
&= \frac{\Bx_1 \cdot \lr{\Bx_0 \wedge \Bx_1} }{\lr{ \Bx_0 \wedge \Bx_1}^2 }.
\end{aligned}
\end{equation}
If we dot with \( \Bx_0 \) and \( \Bx_1 \) respectively, we find
\begin{equation}\label{eqn:reciprocalblog:1800}
\begin{aligned}
\Bx_0 \cdot \Bx^0
&=
\Bx_0 \cdot \frac{ \Bx_1 \cdot \lr{ \Bx_0 \wedge \Bx_1 } }{\lr{ \Bx_0 \wedge \Bx_1}^2 } \\
&=
\lr{ \Bx_0 \wedge \Bx_1 } \cdot \frac{ \Bx_0 \wedge \Bx_1 }{\lr{ \Bx_0 \wedge \Bx_1}^2 }.
\end{aligned}
\end{equation}
We end up with unity as expected. Here the
“factored” out vector is reincorporated into the pseudoscalar using the distribution identity \ref{eqn:reciprocalblog:2280}.
Similarly, dotting with \( \Bx_1 \), we find
\begin{equation}\label{eqn:reciprocalblog:0810}
\begin{aligned}
\Bx_1 \cdot \Bx^0
&=
\Bx_1 \cdot \frac{ \Bx_1 \cdot \lr{ \Bx_0 \wedge \Bx_1 } }{\lr{ \Bx_0 \wedge \Bx_1}^2 } \\
&=
\lr{ \Bx_1 \wedge \Bx_1 } \cdot \frac{ \Bx_0 \wedge \Bx_1 }{\lr{ \Bx_0 \wedge \Bx_1}^2 }.
\end{aligned}
\end{equation}
This is zero, since wedging a vector with itself is zero. We can perform such an operation in reverse, taking the square of the tangent space pseudoscalar, and factoring out one of the basis vectors. After this, division by that squared pseudoscalar will normalize things.

For a three parameter tangent space with basis \( \setlr{ \Bx_0, \Bx_1, \Bx_2 } \), we can factor out any of the tangent vectors like so
\begin{equation}\label{eqn:reciprocalblog:1880}
\begin{aligned}
\lr{ \Bx_0 \wedge \Bx_1 \wedge \Bx_2 }^2
&= \Bx_0 \cdot \lr{ \lr{ \Bx_1 \wedge \Bx_2 } \cdot \lr{ \Bx_0 \wedge \Bx_1 \wedge \Bx_2 } } \\
&= (-1) \Bx_1 \cdot \lr{ \lr{ \Bx_0 \wedge \Bx_2 } \cdot \lr{ \Bx_0 \wedge \Bx_1 \wedge \Bx_2 } } \\
&= (-1)^2 \Bx_2 \cdot \lr{ \lr{ \Bx_0 \wedge \Bx_1 } \cdot \lr{ \Bx_0 \wedge \Bx_1 \wedge \Bx_2 } }.
\end{aligned}
\end{equation}
The toggling of sign reflects the number of permutations required to move the vector of interest to the front of the wedge sequence. Having factored out any one of the vectors, we can rearrange to find that vector that is it’s inverse and perpendicular to all the others.
\begin{equation}\label{eqn:reciprocalblog:1900}
\begin{aligned}
\Bx^0 &= (-1)^0 \lr{ \Bx_1 \wedge \Bx_2 } \cdot \inv{ \Bx_0 \wedge \Bx_1 \wedge \Bx_2 } \\
\Bx^1 &= (-1)^1 \lr{ \Bx_0 \wedge \Bx_2 } \cdot \inv{ \Bx_0 \wedge \Bx_1 \wedge \Bx_2 } \\
\Bx^2 &= (-1)^2 \lr{ \Bx_0 \wedge \Bx_1 } \cdot \inv{ \Bx_0 \wedge \Bx_1 \wedge \Bx_2 }.
\end{aligned}
\end{equation}

End proof.

In the fashion above, should we want the reciprocal frame for all of spacetime given dimension 4 tangent space, we can state it trivially
\begin{equation}\label{eqn:reciprocalblog:1920}
\begin{aligned}
\Bx^0 &= (-1)^0 \lr{ \Bx_1 \wedge \Bx_2 \wedge \Bx_3 } \cdot \inv{ \Bx_0 \wedge \Bx_1 \wedge \Bx_2 \wedge \Bx_3 } \\
\Bx^1 &= (-1)^1 \lr{ \Bx_0 \wedge \Bx_2 \wedge \Bx_3 } \cdot \inv{ \Bx_0 \wedge \Bx_1 \wedge \Bx_2 \wedge \Bx_3 } \\
\Bx^2 &= (-1)^2 \lr{ \Bx_0 \wedge \Bx_1 \wedge \Bx_3 } \cdot \inv{ \Bx_0 \wedge \Bx_1 \wedge \Bx_2 \wedge \Bx_3 } \\
\Bx^3 &= (-1)^3 \lr{ \Bx_0 \wedge \Bx_1 \wedge \Bx_2 } \cdot \inv{ \Bx_0 \wedge \Bx_1 \wedge \Bx_2 \wedge \Bx_3 }.
\end{aligned}
\end{equation}
This is probably not an efficient way to compute all these reciprocals, since we can utilize a single matrix inversion to solve them in one shot. However, there are theoretical advantages to this construction that will be useful when we get to integration theory.

On degeneracy.

A small mention of degeneracy was mentioned above. Regardless of metric, \( \Bx_0 \wedge \Bx_1 = 0 \) means that this pair of vectors are colinear. A tangent space with such a pseudoscalar is clearly undesirable, and we must construct parameterizations for which the area element is non-zero in all regions of interest.

Things get more interesting in mixed signature spaces where we can have vectors that square to zero (i.e. lightlike). If the tangent space pseudoscalar has a lightlike factor, then that pseudoscalar will not be invertible. Such a degeneracy will will likely lead to many other troubles, and parameterizations of this sort should be avoided.

This following problem illustrates an example of this sort of degenerate parameterization.

Problem: Degenerate surface parameterization.

Given a spacetime plane parameterization \( x(u,v) = u a + v b \), where
\begin{equation}\label{eqn:reciprocalblog:480}
a = \gamma_0 + \gamma_1 + \gamma_2 + \gamma_3,
\end{equation}
\begin{equation}\label{eqn:reciprocalblog:500}
b = \gamma_0 – \gamma_1 + \gamma_2 – \gamma_3,
\end{equation}
show that this is a degenerate parameterization, and find the bivector that represents the tangent space. Are these vectors lightlike, spacelike, or timelike? Comment on whether this parameterization represents a physically relevant spacetime surface.

Answer

To characterize the vectors, we square them
\begin{equation}\label{eqn:reciprocalblog:1080}
a^2 = b^2 =
\gamma_0^2 +
\gamma_1^2 +
\gamma_2^2 +
\gamma_3^2
=
1 – 3
= -2,
\end{equation}
so \( a, b \) are both spacelike vectors. The tangent space is clearly just \( \mbox{Span}\setlr{ a, b } = \mbox{Span}\setlr{ e, f }\) where
\begin{equation}\label{eqn:reciprocalblog:1100}
\begin{aligned}
e &= \gamma_0 + \gamma_2 \\
f &= \gamma_1 + \gamma_3.
\end{aligned}
\end{equation}
Observe that \( a = e + f, b = e – f \), and \( e \) is lightlike (\( e^2 = 0 \)), whereas \( f \) is spacelike (\( f^2 = -2 \)), and \( e \cdot f = 0 \), so \( e f = – f e \). The bivector for the tangent plane is
\begin{equation}\label{eqn:reciprocalblog:1120}
\gpgradetwo{
a b
}
=
\gpgradetwo{
(e + f) (e – f)
}
=
\gpgradetwo{
e^2 – f^2 – 2 e f
}
= -2 e f,
\end{equation}
where
\begin{equation}\label{eqn:reciprocalblog:1140}
e f = \gamma_{01} + \gamma_{21} + \gamma_{23} + \gamma_{03}.
\end{equation}
Because \( e \) is lightlike (zero square), and \( e f = – f e \),
the bivector \( e f \) squares to zero
\begin{equation}\label{eqn:reciprocalblog:1780}
\lr{ e f }^2
= -e^2 f^2
= 0,
\end{equation}
which shows that the parameterization is degenerate.

This parameterization can also be expressed as
\begin{equation}\label{eqn:reciprocalblog:1160}
x(u,v)
= u ( e + f ) + v ( e – f )
= (u + v) e + (u – v) f,
\end{equation}
a linear combination of a lightlike and spacelike vector. Intuitively, we expect that a physically meaningful spacetime surface involves linear combinations spacelike vectors, or combinations of a timelike vector with spacelike vectors. This beastie is something entirely different.

Final notes.

There are a few loose ends above. In particular, we haven’t conclusively proven that the set of reciprocal vectors \( \Bx^\mu = \grad u^\mu \) are exactly those obtained through algebraic means. For a full parameterization of spacetime, they are necessarily the same, since both are unique. So we know that \ref{eqn:reciprocalblog:1920} must equal the reciprocals obtained by evaluating the gradient for a full parameterization (and this must also equal the reciprocals that we can obtain through matrix inversion.) We have also not proved explicitly that the three parameter construction of the reciprocals in \ref{eqn:reciprocalblog:1900} is in the tangent space, but that is a fairly trivial observation, so that can be left as an exercise for the reader dismissal. Some additional thought about this is probably required, but it seems reasonable to put that on the back burner and move on to some applications.

References

[1] Peeter Joot. Geometric Algebra for Electrical Engineers. Kindle Direct Publishing, 2019.

Lorentz boosts in Geometric Algebra paravector notation.

January 14, 2018 math and physics play , , , , , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

Motivation.

The notation I prefer for relativistic geometric algebra uses Hestenes’ space time algebra (STA) [2], where the basis is a four dimensional space \( \setlr{ \gamma_\mu } \), subject to Dirac matrix like relations \( \gamma_\mu \cdot \gamma_\nu = \eta_{\mu \nu} \).

In this formalism a four vector is just the sum of the products of coordinates and basis vectors, for example, using summation convention

\begin{equation}\label{eqn:boostToParavector:160}
x = x^\mu \gamma_\mu.
\end{equation}

The invariant for a four-vector in STA is just the square of that vector

\begin{equation}\label{eqn:boostToParavector:180}
\begin{aligned}
x^2
&= (x^\mu \gamma_\mu) \cdot (x^\nu \gamma_\nu) \\
&= \sum_\mu (x^\mu)^2 (\gamma_\mu)^2 \\
&= (x^0)^2 – \sum_{k = 1}^3 (x^k)^2 \\
&= (ct)^2 – \Bx^2.
\end{aligned}
\end{equation}

Recall that a four-vector is time-like if this squared-length is positive, spacelike if negative, and light-like when zero.

Time-like projections are possible by dotting with the “lab-frame” time like basis vector \( \gamma_0 \)

\begin{equation}\label{eqn:boostToParavector:200}
ct = x \cdot \gamma_0 = x^0,
\end{equation}

and space-like projections are wedges with the same

\begin{equation}\label{eqn:boostToParavector:220}
\Bx = x \cdot \gamma_0 = x^k \sigma_k,
\end{equation}

where sums over Latin indexes \( k \in \setlr{1,2,3} \) are implied, and where the elements \( \sigma_k \)

\begin{equation}\label{eqn:boostToParavector:80}
\sigma_k = \gamma_k \gamma_0.
\end{equation}

which are bivectors in STA, can be viewed as an Euclidean vector basis \( \setlr{ \sigma_k } \).

Rotations in STA involve exponentials of space like bivectors \( \theta = a_{ij} \gamma_i \wedge \gamma_j \)

\begin{equation}\label{eqn:boostToParavector:240}
x’ = e^{ \theta/2 } x e^{ -\theta/2 }.
\end{equation}

Boosts, on the other hand, have exactly the same form, but the exponentials are with respect to space-time bivectors arguments, such as \( \theta = a \wedge \gamma_0 \), where \( a \) is any four-vector.

Observe that both boosts and rotations necessarily conserve the space-time length of a four vector (or any multivector with a scalar square).

\begin{equation}\label{eqn:boostToParavector:260}
\begin{aligned}
\lr{x’}^2
&=
\lr{ e^{ \theta/2 } x e^{ -\theta/2 } } \lr{ e^{ \theta/2 } x e^{ -\theta/2 } } \\
&=
e^{ \theta/2 } x \lr{ e^{ -\theta/2 } e^{ \theta/2 } } x e^{ -\theta/2 } \\
&=
e^{ \theta/2 } x^2 e^{ -\theta/2 } \\
&=
x^2 e^{ \theta/2 } e^{ -\theta/2 } \\
&=
x^2.
\end{aligned}
\end{equation}

Paravectors.

Paravectors, as used by Baylis [1], represent four-vectors using a Euclidean multivector basis \( \setlr{ \Be_\mu } \), where \( \Be_0 = 1 \). The conversion between STA and paravector notation requires only multiplication with the timelike basis vector for the lab frame \( \gamma_0 \)

\begin{equation}\label{eqn:boostToParavector:40}
\begin{aligned}
X
&= x \gamma_0 \\
&= \lr{ x^0 \gamma_0 + x^k \gamma_k } \gamma_0 \\
&= x^0 + x^k \gamma_k \gamma_0 \\
&= x^0 + \Bx \\
&= c t + \Bx,
\end{aligned}
\end{equation}

We need a different structure for the invariant length in paravector form. That invariant length is
\begin{equation}\label{eqn:boostToParavector:280}
\begin{aligned}
x^2
&=
\lr{ \lr{ ct + \Bx } \gamma_0 }
\lr{ \lr{ ct + \Bx } \gamma_0 } \\
&=
\lr{ \lr{ ct + \Bx } \gamma_0 }
\lr{ \gamma_0 \lr{ ct – \Bx } } \\
&=
\lr{ ct + \Bx }
\lr{ ct – \Bx }.
\end{aligned}
\end{equation}

Baylis introduces an involution operator \( \overline{{M}} \) which toggles the sign of any vector or bivector grades of a multivector. For example, if \( M = a + \Ba + I \Bb + I c \), where \( a,c \in \mathbb{R} \) and \( \Ba, \Bb \in \mathbb{R}^3 \) is a multivector with all grades \( 0,1,2,3 \), then the involution of \( M \) is

\begin{equation}\label{eqn:boostToParavector:300}
\overline{{M}} = a – \Ba – I \Bb + I c.
\end{equation}

Utilizing this operator, the invariant length for a paravector \( X \) is \( X \overline{{X}} \).

Let’s consider how boosts and rotations can be expressed in the paravector form. The half angle operator for a boost along the spacelike \( \Bv = v \vcap \) direction has the form

\begin{equation}\label{eqn:boostToParavector:120}
L = e^{ -\vcap \phi/2 },
\end{equation}

\begin{equation}\label{eqn:boostToParavector:140}
\begin{aligned}
X’
&=
c t’ + \Bx’ \\
&=
x’ \gamma_0 \\
&=
L x L^\dagger \\
&=
e^{ -\vcap \phi/2 } x^\mu \gamma_\mu
e^{ \vcap \phi/2 } \gamma_0 \\
&=
e^{ -\vcap \phi/2 } x^\mu \gamma_\mu \gamma_0
e^{ -\vcap \phi/2 } \\
&=
e^{ -\vcap \phi/2 } \lr{ x^0 + \Bx } e^{ -\vcap \phi/2 } \\
&=
L X L.
\end{aligned}
\end{equation}

Because the involution operator toggles the sign of vector grades, it is easy to see that the required invariance is maintained

\begin{equation}\label{eqn:boostToParavector:320}
\begin{aligned}
X’ \overline{{X’}}
&=
L X L
\overline{{ L X L }} \\
&=
L X L
\overline{{ L }} \overline{{ X }} \overline{{ L }} \\
&=
L X \overline{{ X }} \overline{{ L }} \\
&=
X \overline{{ X }} L \overline{{ L }} \\
&=
X \overline{{ X }}.
\end{aligned}
\end{equation}

Let’s explicitly expand the transformation of \ref{eqn:boostToParavector:140}, so we can relate the rapidity angle \( \phi \) to the magnitude of the velocity. This is most easily done by splitting the spacelike component \( \Bx \) of the four vector into its projective and rejective components

\begin{equation}\label{eqn:boostToParavector:340}
\begin{aligned}
\Bx
&= \vcap \vcap \Bx \\
&= \vcap \lr{ \vcap \cdot \Bx + \vcap \wedge \Bx } \\
&= \vcap \lr{ \vcap \cdot \Bx } + \vcap \lr{ \vcap \wedge \Bx } \\
&= \Bx_\parallel + \Bx_\perp.
\end{aligned}
\end{equation}

The exponential

\begin{equation}\label{eqn:boostToParavector:360}
e^{-\vcap \phi/2}
=
\cosh\lr{ \phi/2 }
– \vcap \sinh\lr{ \phi/2 },
\end{equation}

commutes with any scalar grades and with \( \Bx_\parallel \), but anticommutes with \( \Bx_\perp \), so

\begin{equation}\label{eqn:boostToParavector:380}
\begin{aligned}
X’
&=
\lr{ c t + \Bx_\parallel } e^{ -\vcap \phi/2 } e^{ -\vcap \phi/2 }
+
\Bx_\perp e^{ \vcap \phi/2 } e^{ -\vcap \phi/2 } \\
&=
\lr{ c t + \Bx_\parallel } e^{ -\vcap \phi }
+
\Bx_\perp \\
&=
\lr{ c t + \vcap \lr{ \vcap \cdot \Bx } } \lr{ \cosh \phi – \vcap \sinh \phi }
+
\Bx_\perp \\
&=
\Bx_\perp
+
\lr{ c t \cosh\phi – \lr{ \vcap \cdot \Bx} \sinh \phi }
+
\vcap \lr{ \lr{ \vcap \cdot \Bx } \cosh\phi – c t \sinh \phi } \\
&=
\Bx_\perp
+
\cosh\phi \lr{ c t – \lr{ \vcap \cdot \Bx} \tanh \phi }
+
\vcap \cosh\phi \lr{ \vcap \cdot \Bx – c t \tanh \phi }.
\end{aligned}
\end{equation}

Employing the argument from [3],
we want \( \phi \) defined so that this has structure of a Galilean transformation in the limit where \( \phi \rightarrow 0 \). This means we equate

\begin{equation}\label{eqn:boostToParavector:400}
\tanh \phi = \frac{v}{c},
\end{equation}

so that for small \(\phi\)

\begin{equation}\label{eqn:boostToParavector:420}
\Bx’ = \Bx – \Bv t.
\end{equation}

We can solving for \( \sinh^2 \phi \) and \( \cosh^2 \phi \) in terms of \( v/c \) using

\begin{equation}\label{eqn:boostToParavector:440}
\tanh^2 \phi
= \frac{v^2}{c^2}
=
\frac{ \sinh^2 \phi }{1 + \sinh^2 \phi}
=
\frac{ \cosh^2 \phi – 1 }{\cosh^2 \phi}.
\end{equation}

which after picking the positive root required for Galilean equivalence gives
\begin{equation}\label{eqn:boostToParavector:460}
\begin{aligned}
\cosh \phi &= \frac{1}{\sqrt{1 – (\Bv/c)^2}} \equiv \gamma \\
\sinh \phi &= \frac{v/c}{\sqrt{1 – (\Bv/c)^2}} = \gamma v/c.
\end{aligned}
\end{equation}

The Lorentz boost, written out in full is

\begin{equation}\label{eqn:boostToParavector:480}
ct’ + \Bx’
=
\Bx_\perp
+
\gamma \lr{ c t – \frac{\Bv}{c} \cdot \Bx }
+
\gamma \lr{ \vcap \lr{ \vcap \cdot \Bx } – \Bv t }
.
\end{equation}

Authors like Chappelle, et al., that also use paravectors [4], specify the form of the Lorentz transformation for the electromagnetic field, but for that transformation reversion is used instead of involution.
I plan to explore that in a later post, starting from the STA formalism that I already understand, and see if I can make sense
of the underlying rationale.

References

[1] William Baylis. Electrodynamics: a modern geometric approach, volume 17. Springer Science \& Business Media, 2004.

[2] C. Doran and A.N. Lasenby. Geometric algebra for physicists. Cambridge University Press New York, Cambridge, UK, 1st edition, 2003.

[3] L. Landau and E. Lifshitz. The Classical theory of fields. Addison-Wesley, 1951.

[4] James M Chappell, Samuel P Drake, Cameron L Seidel, Lachlan J Gunn, and Derek Abbott. Geometric algebra for electrical and electronic engineers. Proceedings of the IEEE, 102 0(9), 2014.