parameterization

Area within closed boundary

August 11, 2024 math and physics play , , , , , ,

[Click here for a PDF version of this post]

Motivation.

On vacation I was reading some more of [1]. It was mentioned in passing that the area contained within a closed parameterized curve is given by
\begin{equation}\label{eqn:containedArea:20}
A = \inv{2} \int_{t_0}^{t_1} \lr{x y’ – y x’} dt,
\end{equation}
where \( x = x(t), y = y(t), t \in [t_0, t_1] \). This has the look of a Stokes theorem coordinate expansion (specifically, the Green’s theorem special case of Stokes’), but with somewhat mysterious looking factor of one half out in front. My aim in this post is to understand the origins of this area relationship, and play with it a bit.

Circular coordinates example.

The book suggests that the reader verify this for a circular parameterization, so we’ll do that here too.

Let
\begin{equation}\label{eqn:containedArea:40}
\begin{aligned}
x(t) &= r \cos t \\
y(t) &= r \sin t,
\end{aligned}
\end{equation}
where \( t \in [0, 2 \pi] \). Plugging in this, we have
\begin{equation}\label{eqn:containedArea:60}
\begin{aligned}
A
&= \inv{2} \int_0^{2 \pi} \lr{ r \cos t \lr{ r \cos t } – r \sin t \lr{ – r \sin t } } dt \\
&= \frac{r^2}{2} \int_0^{2 \pi} \lr{ \cos^2 t + \sin^2 t } dt \\
&= \frac{2 \pi r^2}{2} \\
&= \pi r^2.
\end{aligned}
\end{equation}
This simple example works out.

Piecewise linear parametrization example.

One parameterization of the unit parallelogram depicted in fig. 1 is

\begin{equation}\label{eqn:containedArea:340}
\begin{aligned}
(x,y) &= (t, 0),\quad t \in [0,1] \\
&= (t, t – 1),\quad t \in [1,2] \\
&= (4 – t, 1),\quad t \in [2,3] \\
&= (4 – t, 4 – t),\quad t \in [3,4]
\end{aligned}
\end{equation}

fig. 1. Parallelogram with unit area.

fig. 1. Parallelogram with unit area.

Respective evaluating of \( x y’ – y x’ \) in each of these regions gives
\begin{equation}\label{eqn:containedArea:360}
\begin{aligned}
(t) (0) – (0)(0) &= 0 \\
(t) (1) – (t-1)(1) &= 1 \\
(4-t)(0) – (1)(-1) &= 1 \\
(4-t)(-1) – (4-t)(-1) &= 0,
\end{aligned}
\end{equation}
and integrating
\begin{equation}\label{eqn:containedArea:380}
\inv{2} \int_0^4 \lr{ x y’ – y x’} dt = \frac{2}{2} = 1,
\end{equation}
as expected. In this example, the directional derivative is not continuous at the corners of the parallelogram, but that is not a requirement (as it should not be, as the area is well defined despite any corners.)

Can we discover this relationship using the Jacobian?

Graphically, I can imagine that we could find this area relationship, by considering a parameterization of a family of nested closed curves, as depicted in fig. 2.

fig. 2. Family of nested closed curves.

fig. 2. Family of nested closed curves.

For such a parameterization, calculating the area is just a Jacobian evaluation
\begin{equation}\label{eqn:containedArea:80}
\begin{aligned}
A
&= \iint \frac{\partial(x, y)}{\partial(u,t)} du dt \\
&= \iint \lr{ \PD{u}{x} \PD{t}{y} – \PD{u}{y} \PD{t}{x} } du dt \\
&= \iint \lr{ \PD{u}{x} y’ – \PD{u}{y} x’ } du dt.
\end{aligned}
\end{equation}
Let’s try to eliminate the \( u \) derivatives using integration by parts, and see what we get.
\begin{equation}\label{eqn:containedArea:100}
\begin{aligned}
A
&= \iint \lr{ \PD{u}{x} y’ – \PD{u}{y} x’ } du dt \\
&= \iint \frac{d}{du} \lr{ x y’ – y x’ } du dt – \iint \lr{ x \PD{u}{y’} – y \PD{u}{x’} } du dt \\
&= \int \lr{ x y’ – y x’ } dt – \iint \lr{ x \PD{u}{y’} – y \PD{u}{x’} } du dt.
\end{aligned}
\end{equation}
This is interesting, as we find the area equation that we are interested (times two), but we have a strange new area equation. Essentially, we have found, assuming we trust the claim in the book, that
\begin{equation}\label{eqn:containedArea:120}
A = 2 A – \iint \lr{ x \PD{u}{y’} – y \PD{u}{x’} } du dt,
\end{equation}
so it seems that the area can also be expressed as
\begin{equation}\label{eqn:containedArea:140}
A = \iint \lr{ x \frac{\partial^2 y}{\partial u \partial t} – y \frac{\partial^2 x}{\partial u \partial t} } du dt.
\end{equation}
Let’s again use the circular parameterization to verify that this works. I won’t try to prove this directly, but instead, we’ll use Stokes’ theorem to prove the stated result, from which we get this second derivative area formula as a side effect by virtue of our integration by parts expansion above.

For the circular parameterization, we have
\begin{equation}\label{eqn:containedArea:160}
\begin{aligned}
A
&= \int_{r = 0}^R dr \int_{t = 0}^{2 \pi} dt \lr{ x \frac{\partial^2 y}{\partial r \partial t} – y \frac{\partial^2 x}{\partial r \partial t} } \\
&= \int_{r = 0}^R dr \int_{t = 0}^{2 \pi} dt \lr{ r \cos t \frac{\partial \sin t}{\partial t} – r \sin t \frac{\partial \cos t}{\partial t} } \\
&= \int_{r = 0}^R r dr \int_{t = 0}^{2 \pi} dt \lr{ \cos^2 t + \sin^2 t } \\
&= \frac{R^2}{2} 2 \pi \\
&= \pi R^2.
\end{aligned}
\end{equation}
This checks out, at least for this one specific circular parameterization.

Area formula derivation using Stokes’ theorem.

Theorem 1.1: Green’s theorem.

\begin{equation}\label{eqn:containedArea:260}
\iint dx dy \lr{ \PD{x}{M} – \PD{y}{L} } = \oint L dx + M dy.
\end{equation}

Start proof:

We start with the general two parameter integration theorem
\begin{equation}\label{eqn:containedArea:180}
\iint F d^2 \Bx \lrpartial G = -\oint F d\Bx G,
\end{equation}
set \( F = 1, G = \Bf \), and apply scalar selection
\begin{equation}\label{eqn:containedArea:200}
\iint \gpgradezero{ d^2 \Bx \lrpartial \Bf } = -\oint d\Bx \cdot \Bf,
\end{equation}
to find the two parameter form of Stokes’ theorem
\begin{equation}\label{eqn:containedArea:220}
\iint d^2 \Bx \cdot \lr{ \spacegrad \wedge \Bf } = -\oint d\Bx \cdot \Bf,
\end{equation}

With a planar parameterization, say \( \Bf = L \Be_1 + M \Be_2 \), we have \( d\Bx \cdot \Bf = L dx + M dy \), and for the LHS
\begin{equation}\label{eqn:containedArea:240}
\begin{aligned}
\iint d^2 \Bx \cdot \lr{ \spacegrad \wedge \Bf }
&=
\iint dx dy \Be_{12}^2
\begin{vmatrix}
\partial_1 & \partial_2 \\
L & M
\end{vmatrix} \\
&=
-\iint dx dy \lr{ \PD{x}{M} – \PD{y}{L} }.
\end{aligned}
\end{equation}

End proof.

Parameterized area equation.

If we wish to evaluate an elementary area, we can pick \( L, M \) such that \( \PDi{x}{M} – \PDi{y}{L} = 1 \). One such selection is
\begin{equation}\label{eqn:containedArea:280}
\begin{aligned}
M &= \frac{x}{2} \\
L &= -\frac{y}{2},
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:containedArea:300}
A = \inv{2} \oint -y dx + x dy = \inv{2} \int \lr{ x y’ – y x’ } dt.
\end{equation}
Clearly, there are other possible choices of \( L, M \) that we could use to find alternate area equations, but this choice seems to be independent of the shape of the region.

References

[1] F.W. Byron and R.W. Fuller. Mathematics of Classical and Quantum Physics. Dover Publications, 1992.

More on time derivatives of integrals.

June 9, 2024 math and physics play , , , , , , , , , , , , ,

[Click here for a PDF version of this post]

Motivation.

I was asked about geometric algebra equivalents for a couple identities found in [1], one for line integrals
\begin{equation}\label{eqn:more_feynmans_trick:20}
\ddt{} \int_{C(t)} \Bf \cdot d\Bx =
\int_{C(t)} \lr{
\PD{t}{\Bf} + \spacegrad \lr{ \Bv \cdot \Bf } – \Bv \cross \lr{ \spacegrad \cross \Bf }
}
\cdot d\Bx,
\end{equation}
and one for area integrals
\begin{equation}\label{eqn:more_feynmans_trick:40}
\ddt{} \int_{S(t)} \Bf \cdot d\BA =
\int_{S(t)} \lr{
\PD{t}{\Bf} + \Bv \lr{ \spacegrad \cdot \Bf } – \spacegrad \cross \lr{ \Bv \cross \Bf }
}
\cdot d\BA.
\end{equation}

Both of these look questionable at first glance, because neither has boundary term. However, they can be transformed with Stokes theorem to
\begin{equation}\label{eqn:more_feynmans_trick:60}
\ddt{} \int_{C(t)} \Bf \cdot d\Bx
=
\int_{C(t)} \lr{
\PD{t}{\Bf} – \Bv \cross \lr{ \spacegrad \cross \Bf }
}
\cdot d\Bx
+
\evalbar{\Bv \cdot \Bf }{\Delta C},
\end{equation}
and
\begin{equation}\label{eqn:more_feynmans_trick:80}
\ddt{} \int_{S(t)} \Bf \cdot d\BA =
\int_{S(t)} \lr{
\PD{t}{\Bf} + \Bv \lr{ \spacegrad \cdot \Bf }
}
\cdot d\BA
–
\oint_{\partial S(t)} \lr{ \Bv \cross \Bf } \cdot d\Bx.
\end{equation}
The area integral derivative is now seen to be a variation of one of the special cases of the Leibniz integral rule, see for example [2]. The author admits that the line integral relationship is not well used, and doesn’t show up in the wikipedia page.

My end goal will be to evaluate the derivative of a general multivector line integral
\begin{equation}\label{eqn:more_feynmans_trick:100}
\ddt{} \int_{C(t)} F d\Bx G,
\end{equation}
and area integral
\begin{equation}\label{eqn:more_feynmans_trick:120}
\ddt{} \int_{S(t)} F d^2\Bx G.
\end{equation}
We’ve derived that line integral result in a different fashion previously, but it’s interesting to see a different approach. Perhaps this approach will lend itself nicely to non-scalar integrands?

Prerequisites.

Definition 1.1: Convective derivative.

The convective derivative,
of \( \phi(t, \Bx(t)) \) is defined as
\begin{equation*}
\frac{D \phi}{D t} = \lim_{\Delta t \rightarrow 0} \frac{ \phi(t + \Delta t, \Bx + \Delta t \Bv) – \phi(t, \Bx)}{\Delta t},
\end{equation*}
where \( \Bv = d\Bx/dt \).

Theorem 1.1: Convective derivative.

The convective derivative operator may be written
\begin{equation*}
\frac{D}{D t} = \PD{t}{} + \Bv \cdot \spacegrad.
\end{equation*}

Start proof:

Let’s write
\begin{equation}\label{eqn:more_feynmans_trick:140}
\begin{aligned}
v_0 &= 1 \\
u_0 &= t + v_0 h \\
u_k &= x_k + v_k h, k \in [1,3] \\
\end{aligned}
\end{equation}

The limit, if it exists, must equal the sum of the individual limits
\begin{equation}\label{eqn:more_feynmans_trick:160}
\frac{D \phi}{D t} = \sum_{\alpha = 0}^3 \lim_{\Delta t \rightarrow 0} \frac{ \phi(u_\alpha + v_\alpha h) – \phi(t, Bx)}{h},
\end{equation}
but that is just a sum of derivitives, which can be evaluated by chain rule
\begin{equation}\label{eqn:more_feynmans_trick:180}
\begin{aligned}
\frac{D \phi}{D t}
&= \sum_{\alpha = 0}^{3} \evalbar{ \PD{u_\alpha}{\phi(u_\alpha)} \PD{h}{u_\alpha} }{h = 0} \\
&= \PD{t}{\phi} + \sum_{k = 1}^3 v_k \PD{x_k}{\phi} \\
&= \lr{ \PD{t}{} + \Bv \cdot \spacegrad } \phi.
\end{aligned}
\end{equation}

End proof.

Definition 1.2: Hestenes overdot notation.

We may use a dot or a tick with a derivative operator, to designate the scope of that operator, allowing it to operate bidirectionally, or in a restricted fashion, holding specific multivector elements constant. This is called the Hestenes overdot notation.Illustrating by example, with multivectors \( F, G \), and allowing the gradient to act bidirectionally, we have
\begin{equation*}
\begin{aligned}
F \spacegrad G
&=
\dot{F} \dot{\spacegrad} G
+
F \dot{\spacegrad} \dot{G} \\
&=
\sum_i \lr{ \partial_i F } \Be_i G + \sum_i F \Be_i \lr{ \partial_i G }.
\end{aligned}
\end{equation*}
The last step is a precise statement of the meaning of the overdot notation, showing that we hold the position of the vector elements of the gradient constant, while the (scalar) partials are allowed to commute, acting on the designated elements.

We will need one additional identity

Lemma 1.1: Gradient of dot product (one constant vector.)

Given vectors \( \Ba, \Bb \) the gradient of their dot product is given by
\begin{equation*}
\spacegrad \lr{ \Ba \cdot \Bb }
= \lr{ \Bb \cdot \spacegrad } \Ba – \Bb \cdot \lr{ \spacegrad \wedge \Ba }
+ \lr{ \Ba \cdot \spacegrad } \Bb – \Ba \cdot \lr{ \spacegrad \wedge \Bb }.
\end{equation*}
If \( \Bb \) is constant, this reduces to
\begin{equation*}
\spacegrad \lr{ \Ba \cdot \Bb }
=
\dot{\spacegrad} \lr{ \dot{\Ba} \cdot \Bb }
= \lr{ \Bb \cdot \spacegrad } \Ba – \Bb \cdot \lr{ \spacegrad \wedge \Ba }.
\end{equation*}

Start proof:

The \( \Bb \) constant case is trivial to prove. We use \( \Ba \cdot \lr{ \Bb \wedge \Bc } = \lr{ \Ba \cdot \Bb} \Bc – \Bb \lr{ \Ba \cdot \Bc } \), and simply expand the vector, curl dot product
\begin{equation}\label{eqn:more_feynmans_trick:200}
\Bb \cdot \lr{ \spacegrad \wedge \Ba }
=
\Bb \cdot \lr{ \dot{\spacegrad} \wedge \dot{\Ba} }
= \lr{ \Bb \cdot \dot{\spacegrad} } \dot{\Ba} – \dot{\spacegrad} \lr{ \dot{\Ba} \cdot \Bb }. \end{equation}
Rearrangement proves that \( \Bb \) constant identity. The more general statement follows from a chain rule evaluation of the gradient, holding each vector constant in turn
\begin{equation}\label{eqn:more_feynmans_trick:320}
\spacegrad \lr{ \Ba \cdot \Bb }
=
\dot{\spacegrad} \lr{ \dot{\Ba} \cdot \Bb }
+
\dot{\spacegrad} \lr{ \dot{\Bb} \cdot \Ba }.
\end{equation}

End proof.

Time derivative of a line integral of a vector field.

We now have all our tools assembled, and can proceed to evaluate the derivative of the line integral. We want to show that

Theorem 1.2:

Given a path parameterized by \( \Bx(\lambda) \), where \( d\Bx = (\PDi{\lambda}{\Bx}) d\lambda \), with points along a \( C(t) \) moving through space at a velocity \( \Bv(\Bx(\lambda)) \), and a vector function \( \Bf = \Bf(t, \Bx(\lambda)) \),
\begin{equation*}
\ddt{} \int_{C(t)} \Bf \cdot d\Bx =
\int_{C(t)} \lr{
\PD{t}{\Bf} + \spacegrad \lr{ \Bf \cdot \Bv } + \Bv \cdot \lr{ \spacegrad \wedge \Bf}
} \cdot d\Bx
\end{equation*}

Start proof:

I’m going to avoid thinking about the rigorous details, like any requirements for curve continuity and smoothness. We will however, specify that the end points are given by \( [\lambda_1, \lambda_2] \). Expanding out the parameterization, we seek to evaluate
\begin{equation}\label{eqn:more_feynmans_trick:240}
\int_{C(t)} \Bf \cdot d\Bx
=
\int_{\lambda_1}^{\lambda_2} \Bf(t, \Bx(\lambda) ) \cdot \frac{\partial \Bx}{\partial \lambda} d\lambda.
\end{equation}
The parametric form nicely moves all the boundary time dependence into the integrand, allowing us to write
\begin{equation}\label{eqn:more_feynmans_trick:260}
\begin{aligned}
\ddt{} \int_{C(t)} \Bf \cdot d\Bx
&=
\lim_{\Delta t \rightarrow 0}
\inv{\Delta t}
\int_{\lambda_1}^{\lambda_2}
\lr{ \Bf(t + \Delta t, \Bx(\lambda) + \Delta t \Bv(\Bx(\lambda) ) \cdot \frac{\partial}{\partial \lambda} \lr{ \Bx + \Delta t \Bv(\Bx(\lambda)) } – \Bf(t, \Bx(\lambda)) \cdot \frac{\partial \Bx}{\partial \lambda} } d\lambda \\
&=
\lim_{\Delta t \rightarrow 0}
\inv{\Delta t}
\int_{\lambda_1}^{\lambda_2}
\lr{ \Bf(t + \Delta t, \Bx(\lambda) + \Delta t \Bv(\Bx(\lambda) ) – \Bf(t, \Bx)} \cdot \frac{\partial \Bx}{\partial \lambda} d\lambda \\
&\quad+
\lim_{\Delta t \rightarrow 0}
\int_{\lambda_1}^{\lambda_2}
\Bf(t + \Delta t, \Bx(\lambda) + \Delta t \Bv(\Bx(\lambda) )) \cdot \PD{\lambda}{}\Bv(\Bx(\lambda)) d\lambda \\
&=
\int_{\lambda_1}^{\lambda_2}
\frac{D \Bf}{Dt} \cdot \frac{\partial \Bx}{\partial \lambda} d\lambda +
\lim_{\Delta t \rightarrow 0}
\int_{\lambda_1}^{\lambda_2}
\Bf(t + \Delta t, \Bx(\lambda) + \Delta t \Bv(\Bx(\lambda) \cdot \frac{\partial}{\partial \lambda} \Bv(\Bx(\lambda)) d\lambda \\
&=
\int_{\lambda_1}^{\lambda_2}
\lr{ \PD{t}{\Bf} + \lr{ \Bv \cdot \spacegrad } \Bf } \cdot \frac{\partial \Bx}{\partial \lambda} d\lambda
+
\int_{\lambda_1}^{\lambda_2}
\Bf \cdot \frac{\partial \Bv}{\partial \lambda} d\lambda
\end{aligned}
\end{equation}
At this point, we have a \( d\Bx \) in the first integrand, and a \( d\Bv \) in the second. We can expand the second integrand, evaluating the derivative using chain rule to find
\begin{equation}\label{eqn:more_feynmans_trick:280}
\begin{aligned}
\Bf \cdot \PD{\lambda}{\Bv}
&=
\sum_i \Bf \cdot \PD{x_i}{\Bv} \PD{\lambda}{x_i} \\
&=
\sum_{i,j} f_j \PD{x_i}{v_j} \PD{\lambda}{x_i} \\
&=
\sum_{j} f_j \lr{ \spacegrad v_j } \cdot \PD{\lambda}{\Bx} \\
&=
\sum_{j} \lr{ \dot{\spacegrad} f_j \dot{v_j} } \cdot \PD{\lambda}{\Bx} \\
&=
\dot{\spacegrad} \lr{ \Bf \cdot \dot{\Bv} } \cdot \PD{\lambda}{\Bx}.
\end{aligned}
\end{equation}
Substitution gives
\begin{equation}\label{eqn:more_feynmans_trick:300}
\begin{aligned}
\ddt{} \int_{C(t)} \Bf \cdot d\Bx
&=
\int_{C(t)}
\lr{ \PD{t}{\Bf} + \lr{ \Bv \cdot \spacegrad } \Bf + \dot{\spacegrad} \lr{ \Bf \cdot \dot{\Bv} } } \cdot \frac{\partial \Bx}{\partial \lambda} d\lambda \\
&=
\int_{C(t)}
\lr{ \PD{t}{\Bf}
+ \spacegrad \lr{ \Bf \cdot \Bv }
+ \lr{ \Bv \cdot \spacegrad } \Bf
– \dot{\spacegrad} \lr{ \dot{\Bf} \cdot \Bv }
} \cdot d\Bx \\
&=
\int_{C(t)}
\lr{ \PD{t}{\Bf}
+ \spacegrad \lr{ \Bf \cdot \Bv }
+ \Bv \cdot \lr{ \spacegrad \wedge \Bf }
} \cdot d\Bx,
\end{aligned}
\end{equation}
where the last simplification utilizes lemma 1.1.

End proof.

Since \( \Ba \cdot \lr{ \Bb \wedge \Bc } = -\Ba \cross \lr{ \Bb \cross \Bc } \), observe that we have also recovered \ref{eqn:more_feynmans_trick:20}.

Time derivative of a line integral of a bivector field.

For a bivector line integral, we have

Theorem 1.3:

Given a path parameterized by \( \Bx(\lambda) \), where \( d\Bx = (\PDi{\lambda}{\Bx}) d\lambda \), with points along a \( C(t) \) moving through space at a velocity \( \Bv(\Bx(\lambda)) \), and a bivector function \( B = B(t, \Bx(\lambda)) \),
\begin{equation*}
\ddt{} \int_{C(t)} B \cdot d\Bx =
\int_{C(t)}
\PD{t}{B} \cdot d\Bx + \lr{ d\Bx \cdot \spacegrad } \lr{ B \cdot \Bv } + \lr{ \lr{ \Bv \wedge d\Bx } \cdot \spacegrad } \cdot B.
\end{equation*}

Start proof:

Skipping the steps that follow our previous proceedure exactly, we have
\begin{equation}\label{eqn:more_feynmans_trick:340}
\ddt{} \int_{C(t)} B \cdot d\Bx =
\int_{C(t)}
\PD{t}{B} \cdot d\Bx + \lr{ \Bv \cdot \spacegrad } B \cdot d\Bx + B \cdot d\Bv.
\end{equation}
Since
\begin{equation}\label{eqn:more_feynmans_trick:360}
\begin{aligned}
B \cdot d\Bv
&= B \cdot \PD{\lambda}{\Bv} d\lambda \\
&= B \cdot \PD{x_i}{\Bv} \PD{\lambda}{x_i} d\lambda \\
&= B \cdot \lr{ \lr{ d\Bx \cdot \spacegrad } \Bv },
\end{aligned}
\end{equation}
we have
\begin{equation}\label{eqn:more_feynmans_trick:380}
\ddt{} \int_{C(t)} B \cdot d\Bx
=
\int_{C(t)}
\PD{t}{B} \cdot d\Bx + \lr{ \Bv \cdot \spacegrad } B \cdot d\Bx + B \cdot \lr{ \lr{ d\Bx \cdot \spacegrad } \Bv } \\
\end{equation}
Let’s reduce the two last terms in this integrand
\begin{equation}\label{eqn:more_feynmans_trick:400}
\begin{aligned}
\lr{ \Bv \cdot \spacegrad } B \cdot d\Bx + B \cdot \lr{ \lr{ d\Bx \cdot \spacegrad } \Bv }
&=
\lr{ \Bv \cdot \spacegrad } B \cdot d\Bx –
\lr{ d\Bx \cdot \dot{\spacegrad} } \lr{ \dot{\Bv} \cdot B } \\
&=
\lr{ \Bv \cdot \spacegrad } B \cdot d\Bx
– \lr{ d\Bx \cdot \spacegrad} \lr{ \Bv \cdot B }
+ \lr{ d\Bx \cdot \dot{\spacegrad} } \lr{ \Bv \cdot \dot{B} } \\
&=
\lr{ d\Bx \cdot \spacegrad} \lr{ B \cdot \Bv }
+ \lr{ \Bv \cdot \dot{\spacegrad} } \dot{B} \cdot d\Bx
+ \lr{ d\Bx \cdot \dot{\spacegrad} } \lr{ \Bv \cdot \dot{B} } \\
&=
\lr{ d\Bx \cdot \spacegrad} \lr{ B \cdot \Bv }
+ \lr{ \Bv \lr{ d\Bx \cdot \spacegrad } – d\Bx \lr{ \Bv \cdot \spacegrad } } \cdot B \\
&=
\lr{ d\Bx \cdot \spacegrad} \lr{ B \cdot \Bv }
+ \lr{ \lr{ \Bv \wedge d\Bx } \cdot \spacegrad } \cdot B.
\end{aligned}
\end{equation}
Back substitution finishes the job.

End proof.

Time derivative of a multivector line integral.

Theorem 1.4: Time derivative of multivector line integral.

Given a path parameterized by \( \Bx(\lambda) \), where \( d\Bx = (\PDi{\lambda}{\Bx}) d\lambda \), with points along a \( C(t) \) moving through space at a velocity \( \Bv(\Bx(\lambda)) \), and multivector functions \( M = M(t, \Bx(\lambda)), N = N(t, \Bx(\lambda)) \),
\begin{equation*}
\ddt{} \int_{C(t)} M d\Bx N =
\int_{C(t)}
\frac{D}{D t} M d\Bx N + M \lr{ \lr{ d\Bx \cdot \dot{\spacegrad} } \dot{\Bv} } N.
\end{equation*}

It is useful to write this out explicitly for clarity
\begin{equation}\label{eqn:more_feynmans_trick:420}
\ddt{} \int_{C(t)} M d\Bx N =
\int_{C(t)}
\PD{t}{M} d\Bx N + M d\Bx \PD{t}{N}
+ \dot{M} \lr{ \Bv \cdot \dot{\spacegrad} } N
+ M \lr{ \Bv \cdot \dot{\spacegrad} } \dot{N}
+ M \lr{ \lr{ d\Bx \cdot \dot{\spacegrad} } \dot{\Bv} } N.
\end{equation}

Proof is left to the reader, but follows the patterns above.

It’s not obvious whether there is a nice way to reduce this, as we did for the scalar valued line integral of a vector function, and the vector valued line integral of a bivector function. In particular, our vector and bivector results had \( \spacegrad \lr{ \Bf \cdot \Bv } \), and \( \spacegrad \lr{ B \cdot \Bv } \) terms respectively, which allows for the boundary term to be evaluated using Stokes’ theorem. Is such a manipulation possible here?

Coming later: surface integrals!

References

[1] Nicholas Kemmer. Vector Analysis: A physicist’s guide to the mathematics of fields in three dimensions. CUP Archive, 1977.

[2] Wikipedia contributors. Leibniz integral rule — Wikipedia, the free encyclopedia. https://en.wikipedia.org/w/index.php?title=Leibniz_integral_rule&oldid=1223666713, 2024. [Online; accessed 22-May-2024].

Unpacking the fundamental theorem of multivector calculus in two dimensions

January 18, 2021 math and physics play , , , , , , , , , , , , , , , , , , ,

Notes.

Due to limitations in the MathJax-Latex package, all the oriented integrals in this blog post should be interpreted as having a clockwise orientation. [See the PDF version of this post for more sophisticated formatting.]

Guts.

Given a two dimensional generating vector space, there are two instances of the fundamental theorem for multivector integration
\begin{equation}\label{eqn:unpackingFundamentalTheorem:20}
\int_S F d\Bx \lrpartial G = \evalbar{F G}{\Delta S},
\end{equation}
and
\begin{equation}\label{eqn:unpackingFundamentalTheorem:40}
\int_S F d^2\Bx \lrpartial G = \oint_{\partial S} F d\Bx G.
\end{equation}
The first case is trivial. Given a parameterizated curve \( x = x(u) \), it just states
\begin{equation}\label{eqn:unpackingFundamentalTheorem:60}
\int_{u(0)}^{u(1)} du \PD{u}{}\lr{FG} = F(u(1))G(u(1)) – F(u(0))G(u(0)),
\end{equation}
for all multivectors \( F, G\), regardless of the signature of the underlying space.

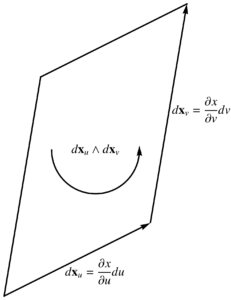
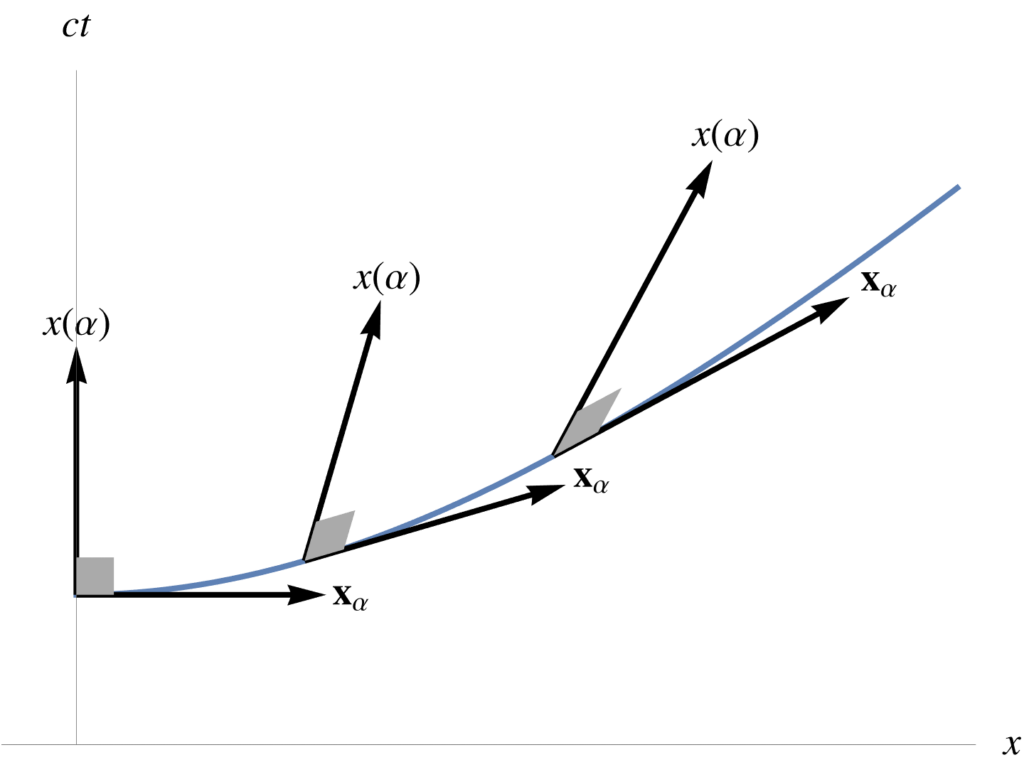
The surface integral is more interesting. Let’s first look at the area element for this surface integral, which is
\begin{equation}\label{eqn:unpackingFundamentalTheorem:80}
d^2 \Bx = d\Bx_u \wedge d \Bx_v.
\end{equation}
Geometrically, this has the area of the parallelogram spanned by \( d\Bx_u \) and \( d\Bx_v \), but weighted by the pseudoscalar of the space. This is explored algebraically in the following problem and illustrated in fig. 1.

fig. 1. 2D vector space and area element.

Problem: Expansion of 2D area bivector.

Let \( \setlr{e_1, e_2} \) be an orthonormal basis for a two dimensional space, with reciprocal frame \( \setlr{e^1, e^2} \). Expand the area bivector \( d^2 \Bx \) in coordinates relating the bivector to the Jacobian and the pseudoscalar.

Answer

With parameterization \( x = x(u,v) = x^\alpha e_\alpha = x_\alpha e^\alpha \), we have
\begin{equation}\label{eqn:unpackingFundamentalTheorem:120}
\Bx_u \wedge \Bx_v
=
\lr{ \PD{u}{x^\alpha} e_\alpha } \wedge
\lr{ \PD{v}{x^\beta} e_\beta }
=
\PD{u}{x^\alpha}
\PD{v}{x^\beta}
e_\alpha
e_\beta
=
\PD{(u,v)}{(x^1,x^2)} e_1 e_2,
\end{equation}
or
\begin{equation}\label{eqn:unpackingFundamentalTheorem:160}
\Bx_u \wedge \Bx_v
=
\lr{ \PD{u}{x_\alpha} e^\alpha } \wedge
\lr{ \PD{v}{x_\beta} e^\beta }
=
\PD{u}{x_\alpha}
\PD{v}{x_\beta}
e^\alpha
e^\beta
=
\PD{(u,v)}{(x_1,x_2)} e^1 e^2.
\end{equation}
The upper and lower index pseudoscalars are related by
\begin{equation}\label{eqn:unpackingFundamentalTheorem:180}
e^1 e^2 e_1 e_2 =
-e^1 e^2 e_2 e_1 =
-1,
\end{equation}
so with \( I = e_1 e_2 \),
\begin{equation}\label{eqn:unpackingFundamentalTheorem:200}
e^1 e^2 = -I^{-1},
\end{equation}
leaving us with
\begin{equation}\label{eqn:unpackingFundamentalTheorem:140}
d^2 \Bx
= \PD{(u,v)}{(x^1,x^2)} du dv\, I
= -\PD{(u,v)}{(x_1,x_2)} du dv\, I^{-1}.
\end{equation}
We see that the area bivector is proportional to either the upper or lower index Jacobian and to the pseudoscalar for the space.

We may write the fundamental theorem for a 2D space as
\begin{equation}\label{eqn:unpackingFundamentalTheorem:680}
\int_S du dv \, \PD{(u,v)}{(x^1,x^2)} F I \lrgrad G = \oint_{\partial S} F d\Bx G,
\end{equation}
where we have dispensed with the vector derivative and use the gradient instead, since they are identical in a two parameter two dimensional space. Of course, unless we are using \( x^1, x^2 \) as our parameterization, we still want the curvilinear representation of the gradient \( \grad = \Bx^u \PDi{u}{} + \Bx^v \PDi{v}{} \).

Problem: Standard basis expansion of fundamental surface relation.

For a parameterization \( x = x^1 e_1 + x^2 e_2 \), where \( \setlr{ e_1, e_2 } \) is a standard (orthogonal) basis, expand the fundamental theorem for surface integrals for the single sided \( F = 1 \) case. Consider functions \( G \) of each grade (scalar, vector, bivector.)

Answer

From \ref{eqn:unpackingFundamentalTheorem:140} we see that the fundamental theorem takes the form
\begin{equation}\label{eqn:unpackingFundamentalTheorem:220}
\int_S dx^1 dx^2\, F I \lrgrad G = \oint_{\partial S} F d\Bx G.
\end{equation}
In a Euclidean space, the operator \( I \lrgrad \), is a \( \pi/2 \) rotation of the gradient, but has a rotated like structure in all metrics:
\begin{equation}\label{eqn:unpackingFundamentalTheorem:240}
I \grad
=
e_1 e_2 \lr{ e^1 \partial_1 + e^2 \partial_2 }
=
-e_2 \partial_1 + e_1 \partial_2.
\end{equation}

  • \( F = 1 \) and \( G \in \bigwedge^0 \) or \( G \in \bigwedge^2 \). For \( F = 1 \) and scalar or bivector \( G \) we have
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:260}
    \int_S dx^1 dx^2\, \lr{ -e_2 \partial_1 + e_1 \partial_2 } G = \oint_{\partial S} d\Bx G,
    \end{equation}
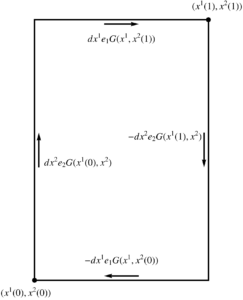
    where, for \( x^1 \in [x^1(0),x^1(1)] \) and \( x^2 \in [x^2(0),x^2(1)] \), the RHS written explicitly is
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:280}
    \oint_{\partial S} d\Bx G
    =
    \int dx^1 e_1
    \lr{ G(x^1, x^2(1)) – G(x^1, x^2(0)) }
    – dx^2 e_2
    \lr{ G(x^1(1),x^2) – G(x^1(0), x^2) }.
    \end{equation}
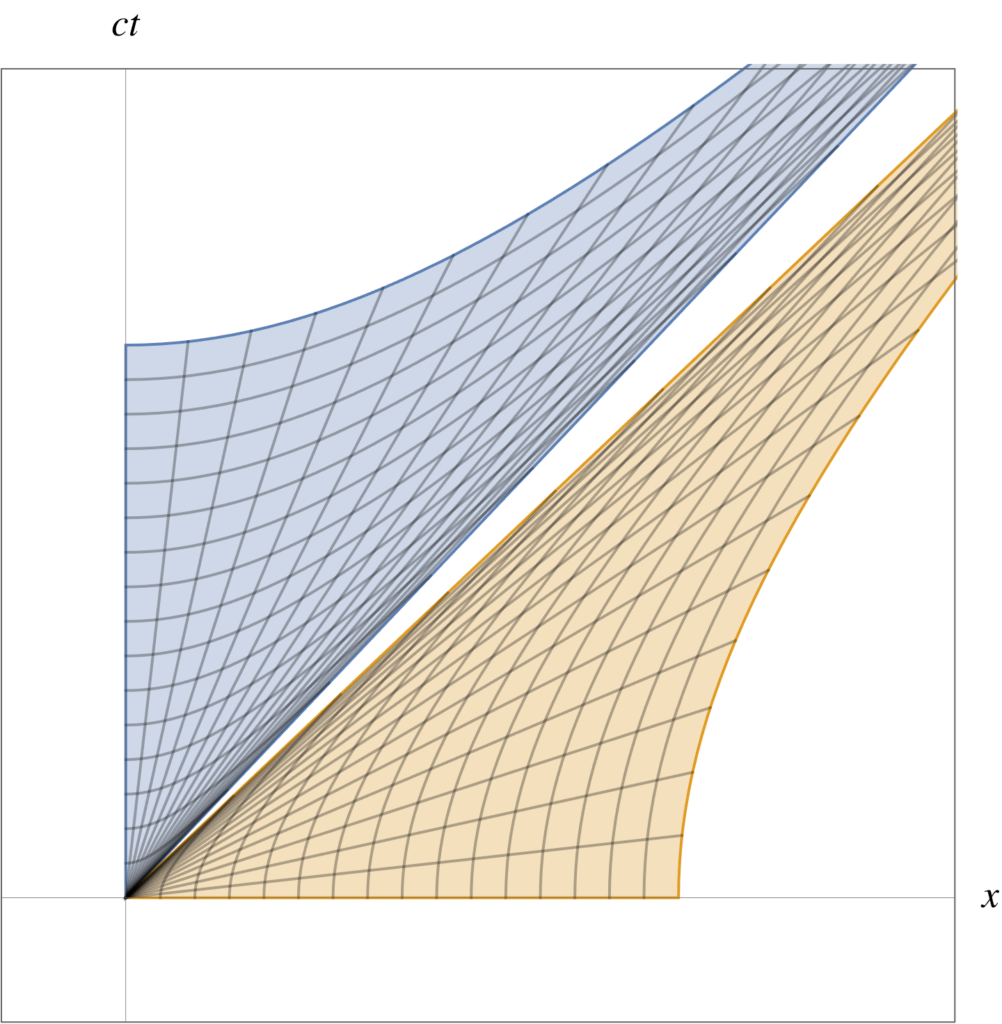
    This is sketched in fig. 2. Since a 2D bivector \( G \) can be written as \( G = I g \), where \( g \) is a scalar, we may write the pseudoscalar case as
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:300}
    \int_S dx^1 dx^2\, \lr{ -e_2 \partial_1 + e_1 \partial_2 } g = \oint_{\partial S} d\Bx g,
    \end{equation}
    after right multiplying both sides with \( I^{-1} \). Algebraically the scalar and pseudoscalar cases can be thought of as identical scalar relationships.
  • \( F = 1, G \in \bigwedge^1 \). For \( F = 1 \) and vector \( G \) the 2D fundamental theorem for surfaces can be split into scalar
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:320}
    \int_S dx^1 dx^2\, \lr{ -e_2 \partial_1 + e_1 \partial_2 } \cdot G = \oint_{\partial S} d\Bx \cdot G,
    \end{equation}
    and bivector relations
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:340}
    \int_S dx^1 dx^2\, \lr{ -e_2 \partial_1 + e_1 \partial_2 } \wedge G = \oint_{\partial S} d\Bx \wedge G.
    \end{equation}
    To expand \ref{eqn:unpackingFundamentalTheorem:320}, let
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:360}
    G = g_1 e^1 + g_2 e^2,
    \end{equation}
    for which
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:380}
    \lr{ -e_2 \partial_1 + e_1 \partial_2 } \cdot G
    =
    \lr{ -e_2 \partial_1 + e_1 \partial_2 } \cdot
    \lr{ g_1 e^1 + g_2 e^2 }
    =
    \partial_2 g_1 – \partial_1 g_2,
    \end{equation}
    and
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:400}
    d\Bx \cdot G
    =
    \lr{ dx^1 e_1 – dx^2 e_2 } \cdot \lr{ g_1 e^1 + g_2 e^2 }
    =
    dx^1 g_1 – dx^2 g_2,
    \end{equation}
    so \ref{eqn:unpackingFundamentalTheorem:320} expands to
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:500}
    \int_S dx^1 dx^2\, \lr{ \partial_2 g_1 – \partial_1 g_2 }
    =
    \int
    \evalbar{dx^1 g_1}{\Delta x^2} – \evalbar{ dx^2 g_2 }{\Delta x^1}.
    \end{equation}
    This coordinate expansion illustrates how the pseudoscalar nature of the area element results in a duality transformation, as we end up with a curl like operation on the LHS, despite the dot product nature of the decomposition that we used. That can also be seen directly for vector \( G \), since
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:560}
    dA (I \grad) \cdot G
    =
    dA \gpgradezero{ I \grad G }
    =
    dA I \lr{ \grad \wedge G },
    \end{equation}
    since the scalar selection of \( I \lr{ \grad \cdot G } \) is zero.In the grade-2 relation \ref{eqn:unpackingFundamentalTheorem:340}, we expect a pseudoscalar cancellation on both sides, leaving a scalar (divergence-like) relationship. This time, we use upper index coordinates for the vector \( G \), letting
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:440}
    G = g^1 e_1 + g^2 e_2,
    \end{equation}
    so
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:460}
    \lr{ -e_2 \partial_1 + e_1 \partial_2 } \wedge G
    =
    \lr{ -e_2 \partial_1 + e_1 \partial_2 } \wedge G
    \lr{ g^1 e_1 + g^2 e_2 }
    =
    e_1 e_2 \lr{ \partial_1 g^1 + \partial_2 g^2 },
    \end{equation}
    and
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:480}
    d\Bx \wedge G
    =
    \lr{ dx^1 e_1 – dx^2 e_2 } \wedge
    \lr{ g^1 e_1 + g^2 e_2 }
    =
    e_1 e_2 \lr{ dx^1 g^2 + dx^2 g^1 }.
    \end{equation}
    So \ref{eqn:unpackingFundamentalTheorem:340}, after multiplication of both sides by \( I^{-1} \), is
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:520}
    \int_S dx^1 dx^2\,
    \lr{ \partial_1 g^1 + \partial_2 g^2 }
    =
    \int
    \evalbar{dx^1 g^2}{\Delta x^2} + \evalbar{dx^2 g^1 }{\Delta x^1}.
    \end{equation}

As before, we’ve implicitly performed a duality transformation, and end up with a divergence operation. That can be seen directly without coordinate expansion, by rewriting the wedge as a grade two selection, and expanding the gradient action on the vector \( G \), as follows
\begin{equation}\label{eqn:unpackingFundamentalTheorem:580}
dA (I \grad) \wedge G
=
dA \gpgradetwo{ I \grad G }
=
dA I \lr{ \grad \cdot G },
\end{equation}
since \( I \lr{ \grad \wedge G } \) has only a scalar component.

 

fig. 2. Line integral around rectangular boundary.

Theorem 1.1: Green’s theorem [1].

Let \( S \) be a Jordan region with a piecewise-smooth boundary \( C \). If \( P, Q \) are continuously differentiable on an open set that contains \( S \), then
\begin{equation*}
\int dx dy \lr{ \PD{y}{P} – \PD{x}{Q} } = \oint P dx + Q dy.
\end{equation*}

Problem: Relationship to Green’s theorem.

If the space is Euclidean, show that \ref{eqn:unpackingFundamentalTheorem:500} and \ref{eqn:unpackingFundamentalTheorem:520} are both instances of Green’s theorem with suitable choices of \( P \) and \( Q \).

Answer

I will omit the subtleties related to general regions and consider just the case of an infinitesimal square region.

Start proof:

Let’s start with \ref{eqn:unpackingFundamentalTheorem:500}, with \( g_1 = P \) and \( g_2 = Q \), and \( x^1 = x, x^2 = y \), the RHS is
\begin{equation}\label{eqn:unpackingFundamentalTheorem:600}
\int dx dy \lr{ \PD{y}{P} – \PD{x}{Q} }.
\end{equation}
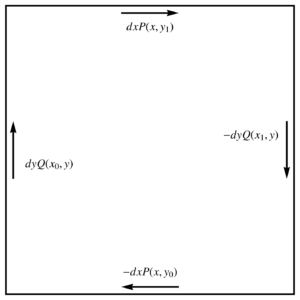
On the RHS we have
\begin{equation}\label{eqn:unpackingFundamentalTheorem:620}
\int \evalbar{dx P}{\Delta y} – \evalbar{ dy Q }{\Delta x}
=
\int dx \lr{ P(x, y_1) – P(x, y_0) } – \int dy \lr{ Q(x_1, y) – Q(x_0, y) }.
\end{equation}
This pair of integrals is plotted in fig. 3, from which we see that \ref{eqn:unpackingFundamentalTheorem:620} can be expressed as the line integral, leaving us with
\begin{equation}\label{eqn:unpackingFundamentalTheorem:640}
\int dx dy \lr{ \PD{y}{P} – \PD{x}{Q} }
=
\oint dx P + dy Q,
\end{equation}
which is Green’s theorem over the infinitesimal square integration region.

For the equivalence of \ref{eqn:unpackingFundamentalTheorem:520} to Green’s theorem, let \( g^2 = P \), and \( g^1 = -Q \). Plugging into the LHS, we find the Green’s theorem integrand. On the RHS, the integrand expands to
\begin{equation}\label{eqn:unpackingFundamentalTheorem:660}
\evalbar{dx g^2}{\Delta y} + \evalbar{dy g^1 }{\Delta x}
=
dx \lr{ P(x,y_1) – P(x, y_0)}
+
dy \lr{ -Q(x_1, y) + Q(x_0, y)},
\end{equation}
which is exactly what we found in \ref{eqn:unpackingFundamentalTheorem:620}.

End proof.

 

fig. 3. Path for Green’s theorem.

We may also relate multivector gradient integrals in 2D to the normal integral around the boundary of the bounding curve. That relationship is as follows.

Theorem 1.2: 2D gradient integrals.

\begin{equation*}
\begin{aligned}
\int J du dv \rgrad G &= \oint I^{-1} d\Bx G = \int J \lr{ \Bx^v du + \Bx^u dv } G \\
\int J du dv F \lgrad &= \oint F I^{-1} d\Bx = \int J F \lr{ \Bx^v du + \Bx^u dv },
\end{aligned}
\end{equation*}
where \( J = \partial(x^1, x^2)/\partial(u,v) \) is the Jacobian of the parameterization \( x = x(u,v) \). In terms of the coordinates \( x^1, x^2 \), this reduces to
\begin{equation*}
\begin{aligned}
\int dx^1 dx^2 \rgrad G &= \oint I^{-1} d\Bx G = \int \lr{ e^2 dx^1 + e^1 dx^2 } G \\
\int dx^1 dx^2 F \lgrad &= \oint G I^{-1} d\Bx = \int F \lr{ e^2 dx^1 + e^1 dx^2 }.
\end{aligned}
\end{equation*}
The vector \( I^{-1} d\Bx \) is orthogonal to the tangent vector along the boundary, and for Euclidean spaces it can be identified as the outwards normal.

Start proof:

Respectively setting \( F = 1 \), and \( G = 1\) in \ref{eqn:unpackingFundamentalTheorem:680}, we have
\begin{equation}\label{eqn:unpackingFundamentalTheorem:940}
\int I^{-1} d^2 \Bx \rgrad G = \oint I^{-1} d\Bx G,
\end{equation}
and
\begin{equation}\label{eqn:unpackingFundamentalTheorem:960}
\int F d^2 \Bx \lgrad I^{-1} = \oint F d\Bx I^{-1}.
\end{equation}
Starting with \ref{eqn:unpackingFundamentalTheorem:940} we find
\begin{equation}\label{eqn:unpackingFundamentalTheorem:700}
\int I^{-1} J du dv I \rgrad G = \oint d\Bx G,
\end{equation}
to find \( \int dx^1 dx^2 \rgrad G = \oint I^{-1} d\Bx G \), as desireed. In terms of a parameterization \( x = x(u,v) \), the pseudoscalar for the space is
\begin{equation}\label{eqn:unpackingFundamentalTheorem:720}
I = \frac{\Bx_u \wedge \Bx_v}{J},
\end{equation}
so
\begin{equation}\label{eqn:unpackingFundamentalTheorem:740}
I^{-1} = \frac{J}{\Bx_u \wedge \Bx_v}.
\end{equation}
Also note that \( \lr{\Bx_u \wedge \Bx_v}^{-1} = \Bx^v \wedge \Bx^u \), so
\begin{equation}\label{eqn:unpackingFundamentalTheorem:760}
I^{-1} = J \lr{ \Bx^v \wedge \Bx^u },
\end{equation}
and
\begin{equation}\label{eqn:unpackingFundamentalTheorem:780}
I^{-1} d\Bx
= I^{-1} \cdot d\Bx
= J \lr{ \Bx^v \wedge \Bx^u } \cdot \lr{ \Bx_u du – \Bx_v dv }
= J \lr{ \Bx^v du + \Bx^u dv },
\end{equation}
so the right acting gradient integral is
\begin{equation}\label{eqn:unpackingFundamentalTheorem:800}
\int J du dv \grad G =
\int
\evalbar{J \Bx^v G}{\Delta v} du + \evalbar{J \Bx^u G dv}{\Delta u},
\end{equation}
which we write in abbreviated form as \( \int J \lr{ \Bx^v du + \Bx^u dv} G \).

For the \( G = 1 \) case, from \ref{eqn:unpackingFundamentalTheorem:960} we find
\begin{equation}\label{eqn:unpackingFundamentalTheorem:820}
\int J du dv F I \lgrad I^{-1} = \oint F d\Bx I^{-1}.
\end{equation}
However, in a 2D space, regardless of metric, we have \( I a = – a I \) for any vector \( a \) (i.e. \( \grad \) or \( d\Bx\)), so we may commute the outer pseudoscalars in
\begin{equation}\label{eqn:unpackingFundamentalTheorem:840}
\int J du dv F I \lgrad I^{-1} = \oint F d\Bx I^{-1},
\end{equation}
so
\begin{equation}\label{eqn:unpackingFundamentalTheorem:850}
-\int J du dv F I I^{-1} \lgrad = -\oint F I^{-1} d\Bx.
\end{equation}
After cancelling the negative sign on both sides, we have the claimed result.

To see that \( I a \), for any vector \( a \) is normal to \( a \), we can compute the dot product
\begin{equation}\label{eqn:unpackingFundamentalTheorem:860}
\lr{ I a } \cdot a
=
\gpgradezero{ I a a }
=
a^2 \gpgradezero{ I }
= 0,
\end{equation}
since the scalar selection of a bivector is zero. Since \( I^{-1} = \pm I \), the same argument shows that \( I^{-1} d\Bx \) must be orthogonal to \( d\Bx \).

End proof.

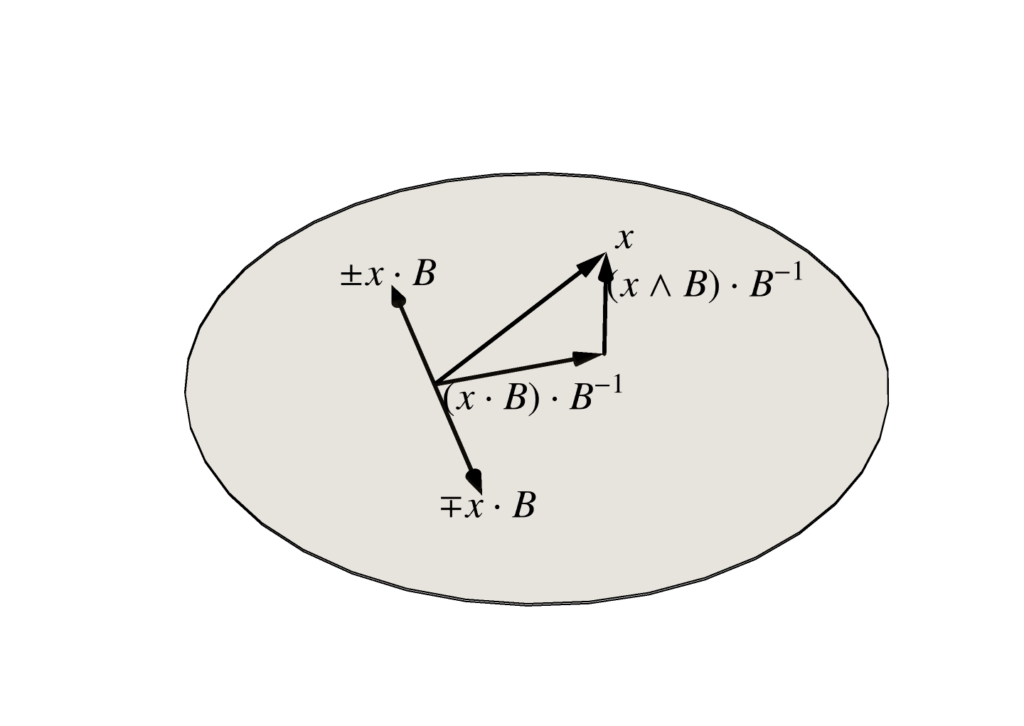
Let’s look at the geometry of the normal \( I^{-1} \Bx \) in a couple 2D vector spaces. We use an integration volume of a unit square to simplify the boundary term expressions.

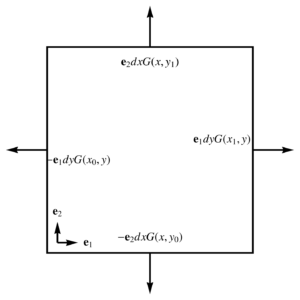
  • Euclidean: With a parameterization \( x(u,v) = u\Be_1 + v \Be_2 \), and Euclidean basis vectors \( (\Be_1)^2 = (\Be_2)^2 = 1 \), the fundamental theorem integrated over the rectangle \( [x_0,x_1] \times [y_0,y_1] \) is
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:880}
    \int dx dy \grad G =
    \int
    \Be_2 \lr{ G(x,y_1) – G(x,y_0) } dx +
    \Be_1 \lr{ G(x_1,y) – G(x_0,y) } dy,
    \end{equation}
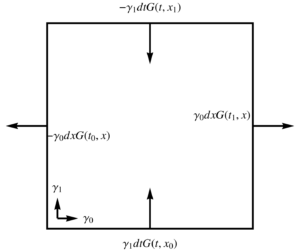
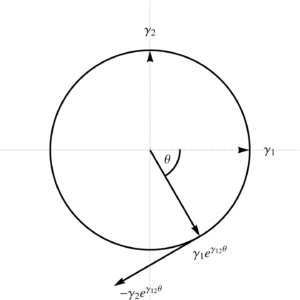
    Each of the terms in the integrand above are illustrated in fig. 4, and we see that this is a path integral weighted by the outwards normal.

    fig. 4. Outwards oriented normal for Euclidean space.

  • Spacetime: Let \( x(u,v) = u \gamma_0 + v \gamma_1 \), where \( (\gamma_0)^2 = -(\gamma_1)^2 = 1 \). With \( u = t, v = x \), the gradient integral over a \([t_0,t_1] \times [x_0,x_1]\) of spacetime is
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:900}
    \begin{aligned}
    \int dt dx \grad G
    &=
    \int
    \gamma^1 dt \lr{ G(t, x_1) – G(t, x_0) }
    +
    \gamma^0 dx \lr{ G(t_1, x) – G(t_1, x) } \\
    &=
    \int
    \gamma_1 dt \lr{ -G(t, x_1) + G(t, x_0) }
    +
    \gamma_0 dx \lr{ G(t_1, x) – G(t_1, x) }
    .
    \end{aligned}
    \end{equation}
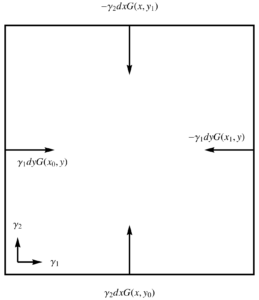
    With \( t \) plotted along the horizontal axis, and \( x \) along the vertical, each of the terms of this integrand is illustrated graphically in fig. 5. For this mixed signature space, there is no longer any good geometrical characterization of the normal.

    fig. 5. Orientation of the boundary normal for a spacetime basis.

  • Spacelike:
    Let \( x(u,v) = u \gamma_1 + v \gamma_2 \), where \( (\gamma_1)^2 = (\gamma_2)^2 = -1 \). With \( u = x, v = y \), the gradient integral over a \([x_0,x_1] \times [y_0,y_1]\) of this space is
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:920}
    \begin{aligned}
    \int dx dy \grad G
    &=
    \int
    \gamma^2 dx \lr{ G(x, y_1) – G(x, y_0) }
    +
    \gamma^1 dy \lr{ G(x_1, y) – G(x_1, y) } \\
    &=
    \int
    \gamma_2 dx \lr{ -G(x, y_1) + G(x, y_0) }
    +
    \gamma_1 dy \lr{ -G(x_1, y) + G(x_1, y) }
    .
    \end{aligned}
    \end{equation}
    Referring to fig. 6. where the elements of the integrand are illustrated, we see that the normal \( I^{-1} d\Bx \) for the boundary of this region can be characterized as inwards.

    fig. 6. Inwards oriented normal for a Dirac spacelike basis.

References

[1] S.L. Salas and E. Hille. Calculus: one and several variables. Wiley New York, 1990.

Fundamental theorem of geometric calculus for line integrals (relativistic.)

December 16, 2020 math and physics play , , , , , , , , , , , , , , , , , , , , , , , , , , ,

[This post is best viewed in PDF form, due to latex elements that I could not format with wordpress mathjax.]

Background for this particular post can be found in

  1. Curvilinear coordinates and gradient in spacetime, and reciprocal frames, and
  2. Lorentz transformations in Space Time Algebra (STA)
  3. A couple more reciprocal frame examples.

Motivation.

I’ve been slowly working my way towards a statement of the fundamental theorem of integral calculus, where the functions being integrated are elements of the Dirac algebra (space time multivectors in the geometric algebra parlance.)

This is interesting because we want to be able to do line, surface, 3-volume and 4-volume space time integrals. We have many \(\mathbb{R}^3\) integral theorems
\begin{equation}\label{eqn:fundamentalTheoremOfGC:40a}
\int_A^B d\Bl \cdot \spacegrad f = f(B) – f(A),
\end{equation}
\begin{equation}\label{eqn:fundamentalTheoremOfGC:60a}
\int_S dA\, \ncap \cross \spacegrad f = \int_{\partial S} d\Bx\, f,
\end{equation}
\begin{equation}\label{eqn:fundamentalTheoremOfGC:80a}
\int_S dA\, \ncap \cdot \lr{ \spacegrad \cross \Bf} = \int_{\partial S} d\Bx \cdot \Bf,
\end{equation}
\begin{equation}\label{eqn:fundamentalTheoremOfGC:100a}
\int_S dx dy \lr{ \PD{y}{P} – \PD{x}{Q} }
=
\int_{\partial S} P dx + Q dy,
\end{equation}
\begin{equation}\label{eqn:fundamentalTheoremOfGC:120a}
\int_V dV\, \spacegrad f = \int_{\partial V} dA\, \ncap f,
\end{equation}
\begin{equation}\label{eqn:fundamentalTheoremOfGC:140a}
\int_V dV\, \spacegrad \cross \Bf = \int_{\partial V} dA\, \ncap \cross \Bf,
\end{equation}
\begin{equation}\label{eqn:fundamentalTheoremOfGC:160a}
\int_V dV\, \spacegrad \cdot \Bf = \int_{\partial V} dA\, \ncap \cdot \Bf,
\end{equation}
and want to know how to generalize these to four dimensions and also make sure that we are handling the relativistic mixed signature correctly. If our starting point was the mess of equations above, we’d be in trouble, since it is not obvious how these generalize. All the theorems with unit normals have to be handled completely differently in four dimensions since we don’t have a unique normal to any given spacetime plane.
What comes to our rescue is the Fundamental Theorem of Geometric Calculus (FTGC), which has the form
\begin{equation}\label{eqn:fundamentalTheoremOfGC:40}
\int F d^n \Bx\, \lrpartial G = \int F d^{n-1} \Bx\, G,
\end{equation}
where \(F,G\) are multivectors functions (i.e. sums of products of vectors.) We’ve seen ([2], [1]) that all the identities above are special cases of the fundamental theorem.

Do we need any special care to state the FTGC correctly for our relativistic case? It turns out that the answer is no! Tangent and reciprocal frame vectors do all the heavy lifting, and we can use the fundamental theorem as is, even in our mixed signature space. The only real change that we need to make is use spacetime gradient and vector derivative operators instead of their spatial equivalents. We will see how this works below. Note that instead of starting with \ref{eqn:fundamentalTheoremOfGC:40} directly, I will attempt to build up to that point in a progressive fashion that is hopefully does not require the reader to make too many unjustified mental leaps.

Multivector line integrals.

We want to define multivector line integrals to start with. Recall that in \(\mathbb{R}^3\) we would say that for scalar functions \( f\), the integral
\begin{equation}\label{eqn:fundamentalTheoremOfGC:180b}
\int d\Bx\, f = \int f d\Bx,
\end{equation}
is a line integral. Also, for vector functions \( \Bf \) we call
\begin{equation}\label{eqn:fundamentalTheoremOfGC:200}
\int d\Bx \cdot \Bf = \inv{2} \int d\Bx\, \Bf + \Bf d\Bx.
\end{equation}
a line integral. In order to generalize line integrals to multivector functions, we will allow our multivector functions to be placed on either or both sides of the differential.

Definition 1.1: Line integral.

Given a single variable parameterization \( x = x(u) \), we write \( d^1\Bx = \Bx_u du \), and call
\begin{equation}\label{eqn:fundamentalTheoremOfGC:220a}
\int F d^1\Bx\, G,
\end{equation}
a line integral, where \( F,G \) are arbitrary multivector functions.

We must be careful not to reorder any of the factors in the integrand, since the differential may not commute with either \( F \) or \( G \). Here is a simple example where the integrand has a product of a vector and differential.

Problem: Circular parameterization.

Given a circular parameterization \( x(\theta) = \gamma_1 e^{-i\theta} \), where \( i = \gamma_1 \gamma_2 \), the unit bivector for the \(x,y\) plane. Compute the line integral
\begin{equation}\label{eqn:fundamentalTheoremOfGC:100}
\int_0^{\pi/4} F(\theta)\, d^1 \Bx\, G(\theta),
\end{equation}
where \( F(\theta) = \Bx^\theta + \gamma_3 + \gamma_1 \gamma_0 \) is a multivector valued function, and \( G(\theta) = \gamma_0 \) is vector valued.

Answer

The tangent vector for the curve is
\begin{equation}\label{eqn:fundamentalTheoremOfGC:60}
\Bx_\theta
= -\gamma_1 \gamma_1 \gamma_2 e^{-i\theta}
= \gamma_2 e^{-i\theta},
\end{equation}
with reciprocal vector \( \Bx^\theta = e^{i \theta} \gamma^2 \). The differential element is \( d^1 \Bx = \gamma_2 e^{-i\theta} d\theta \), so the integrand is
\begin{equation}\label{eqn:fundamentalTheoremOfGC:80}
\begin{aligned}
\int_0^{\pi/4} \lr{ \Bx^\theta + \gamma_3 + \gamma_1 \gamma_0 } d^1 \Bx\, \gamma_0
&=
\int_0^{\pi/4} \lr{ e^{i\theta} \gamma^2 + \gamma_3 + \gamma_1 \gamma_0 } \gamma_2 e^{-i\theta} d\theta\, \gamma_0 \\
&=
\frac{\pi}{4} \gamma_0 + \lr{ \gamma_{32} + \gamma_{102} } \inv{-i} \lr{ e^{-i\pi/4} – 1 } \gamma_0 \\
&=
\frac{\pi}{4} \gamma_0 + \inv{\sqrt{2}} \lr{ \gamma_{32} + \gamma_{102} } \gamma_{120} \lr{ 1 – \gamma_{12} } \\
&=
\frac{\pi}{4} \gamma_0 + \inv{\sqrt{2}} \lr{ \gamma_{310} + 1 } \lr{ 1 – \gamma_{12} }.
\end{aligned}
\end{equation}
Observe how care is required not to reorder any terms. This particular end result is a multivector with scalar, vector, bivector, and trivector grades, but no pseudoscalar component. The grades in the end result depend on both the function in the integrand and on the path. For example, had we integrated all the way around the circle, the end result would have been the vector \( 2 \pi \gamma_0 \) (i.e. a \( \gamma_0 \) weighted unit circle circumference), as all the other grades would have been killed by the complex exponential integrated over a full period.

Problem: Line integral for boosted time direction vector.

Let \( x = e^{\vcap \alpha/2} \gamma_0 e^{-\vcap \alpha/2} \) represent the spacetime curve of all the boosts of \( \gamma_0 \) along a specific velocity direction vector, where \( \vcap = (v \wedge \gamma_0)/\Norm{v \wedge \gamma_0} \) is a unit spatial bivector for any constant vector \( v \). Compute the line integral
\begin{equation}\label{eqn:fundamentalTheoremOfGC:240}
\int x\, d^1 \Bx.
\end{equation}

Answer

Observe that \( \vcap \) and \( \gamma_0 \) anticommute, so we may write our boost as a one sided exponential
\begin{equation}\label{eqn:fundamentalTheoremOfGC:260}
x(\alpha) = \gamma_0 e^{-\vcap \alpha} = e^{\vcap \alpha} \gamma_0 = \lr{ \cosh\alpha + \vcap \sinh\alpha } \gamma_0.
\end{equation}
The tangent vector is just
\begin{equation}\label{eqn:fundamentalTheoremOfGC:280}
\Bx_\alpha = \PD{\alpha}{x} = e^{\vcap\alpha} \vcap \gamma_0.
\end{equation}
Let’s get a bit of intuition about the nature of this vector. It’s square is
\begin{equation}\label{eqn:fundamentalTheoremOfGC:300}
\begin{aligned}
\Bx_\alpha^2
&=
e^{\vcap\alpha} \vcap \gamma_0
e^{\vcap\alpha} \vcap \gamma_0 \\
&=
-e^{\vcap\alpha} \vcap e^{-\vcap\alpha} \vcap (\gamma_0)^2 \\
&=
-1,
\end{aligned}
\end{equation}
so we see that the tangent vector is a spacelike unit vector. As the vector representing points on the curve is necessarily timelike (due to Lorentz invariance), these two must be orthogonal at all points. Let’s confirm this algebraically
\begin{equation}\label{eqn:fundamentalTheoremOfGC:320}
\begin{aligned}
x \cdot \Bx_\alpha
&=
\gpgradezero{ e^{\vcap \alpha} \gamma_0 e^{\vcap \alpha} \vcap \gamma_0 } \\
&=
\gpgradezero{ e^{-\vcap \alpha} e^{\vcap \alpha} \vcap (\gamma_0)^2 } \\
&=
\gpgradezero{ \vcap } \\
&= 0.
\end{aligned}
\end{equation}
Here we used \( e^{\vcap \alpha} \gamma_0 = \gamma_0 e^{-\vcap \alpha} \), and \( \gpgradezero{A B} = \gpgradezero{B A} \). Geometrically, we have the curious fact that the direction vectors to points on the curve are perpendicular (with respect to our relativistic dot product) to the tangent vectors on the curve, as illustrated in fig. 1.

fig. 1. Tangent perpendicularity in mixed metric.

Perfect differentials.

Having seen a couple examples of multivector line integrals, let’s now move on to figure out the structure of a line integral that has a “perfect” differential integrand. We can take a hint from the \(\mathbb{R}^3\) vector result that we already know, namely
\begin{equation}\label{eqn:fundamentalTheoremOfGC:120}
\int_A^B d\Bl \cdot \spacegrad f = f(B) – f(A).
\end{equation}
It seems reasonable to guess that the relativistic generalization of this is
\begin{equation}\label{eqn:fundamentalTheoremOfGC:140}
\int_A^B dx \cdot \grad f = f(B) – f(A).
\end{equation}
Let’s check that, by expanding in coordinates
\begin{equation}\label{eqn:fundamentalTheoremOfGC:160}
\begin{aligned}
\int_A^B dx \cdot \grad f
&=
\int_A^B d\tau \frac{dx^\mu}{d\tau} \partial_\mu f \\
&=
\int_A^B d\tau \frac{dx^\mu}{d\tau} \PD{x^\mu}{f} \\
&=
\int_A^B d\tau \frac{df}{d\tau} \\
&=
f(B) – f(A).
\end{aligned}
\end{equation}
If we drop the dot product, will we have such a nice result? Let’s see:
\begin{equation}\label{eqn:fundamentalTheoremOfGC:180}
\begin{aligned}
\int_A^B dx \grad f
&=
\int_A^B d\tau \frac{dx^\mu}{d\tau} \gamma_\mu \gamma^\nu \partial_\nu f \\
&=
\int_A^B d\tau \frac{dx^\mu}{d\tau} \PD{x^\mu}{f}
+
\int_A^B
d\tau
\sum_{\mu \ne \nu} \gamma_\mu \gamma^\nu
\frac{dx^\mu}{d\tau} \PD{x^\nu}{f}.
\end{aligned}
\end{equation}
This scalar component of this integrand is a perfect differential, but the bivector part of the integrand is a complete mess, that we have no hope of generally integrating. It happens that if we consider one of the simplest parameterization examples, we can get a strong hint of how to generalize the differential operator to one that ends up providing a perfect differential. In particular, let’s integrate over a linear constant path, such as \( x(\tau) = \tau \gamma_0 \). For this path, we have
\begin{equation}\label{eqn:fundamentalTheoremOfGC:200a}
\begin{aligned}
\int_A^B dx \grad f
&=
\int_A^B \gamma_0 d\tau \lr{
\gamma^0 \partial_0 +
\gamma^1 \partial_1 +
\gamma^2 \partial_2 +
\gamma^3 \partial_3 } f \\
&=
\int_A^B d\tau \lr{
\PD{\tau}{f} +
\gamma_0 \gamma^1 \PD{x^1}{f} +
\gamma_0 \gamma^2 \PD{x^2}{f} +
\gamma_0 \gamma^3 \PD{x^3}{f}
}.
\end{aligned}
\end{equation}
Just because the path does not have any \( x^1, x^2, x^3 \) component dependencies does not mean that these last three partials are neccessarily zero. For example \( f = f(x(\tau)) = \lr{ x^0 }^2 \gamma_0 + x^1 \gamma_1 \) will have a non-zero contribution from the \( \partial_1 \) operator. In that particular case, we can easily integrate \( f \), but we have to know the specifics of the function to do the integral. However, if we had a differential operator that did not include any component off the integration path, we would ahve a perfect differential. That is, if we were to replace the gradient with the projection of the gradient onto the tangent space, we would have a perfect differential. We see that the function of the dot product in \ref{eqn:fundamentalTheoremOfGC:140} has the same effect, as it rejects any component of the gradient that does not lie on the tangent space.

Definition 1.2: Vector derivative.

Given a spacetime manifold parameterized by \( x = x(u^0, \cdots u^{N-1}) \), with tangent vectors \( \Bx_\mu = \PDi{u^\mu}{x} \), and reciprocal vectors \( \Bx^\mu \in \textrm{Span}\setlr{\Bx_\nu} \), such that \( \Bx^\mu \cdot \Bx_\nu = {\delta^\mu}_\nu \), the vector derivative is defined as
\begin{equation}\label{eqn:fundamentalTheoremOfGC:240a}
\partial = \sum_{\mu = 0}^{N-1} \Bx^\mu \PD{u^\mu}{}.
\end{equation}
Observe that if this is a full parameterization of the space (\(N = 4\)), then the vector derivative is identical to the gradient. The vector derivative is the projection of the gradient onto the tangent space at the point of evaluation.Furthermore, we designate \( \lrpartial \) as the vector derivative allowed to act bidirectionally, as follows
\begin{equation}\label{eqn:fundamentalTheoremOfGC:260a}
R \lrpartial S
=
R \Bx^\mu \PD{u^\mu}{S}
+
\PD{u^\mu}{R} \Bx^\mu S,
\end{equation}
where \( R, S \) are multivectors, and summation convention is implied. In this bidirectional action,
the vector factors of the vector derivative must stay in place (as they do not neccessarily commute with \( R,S\)), but the derivative operators apply in a chain rule like fashion to both functions.

Noting that \( \Bx_u \cdot \grad = \Bx_u \cdot \partial \), we may rewrite the scalar line integral identity \ref{eqn:fundamentalTheoremOfGC:140} as
\begin{equation}\label{eqn:fundamentalTheoremOfGC:220}
\int_A^B dx \cdot \partial f = f(B) – f(A).
\end{equation}
However, as our example hinted at, the fundamental theorem for line integrals has a multivector generalization that does not rely on a dot product to do the tangent space filtering, and is more powerful. That generalization has the following form.

Theorem 1.1: Fundamental theorem for line integrals.

Given multivector functions \( F, G \), and a single parameter curve \( x(u) \) with line element \( d^1 \Bx = \Bx_u du \), then
\begin{equation}\label{eqn:fundamentalTheoremOfGC:280a}
\int_A^B F d^1\Bx \lrpartial G = F(B) G(B) – F(A) G(A).
\end{equation}

Start proof:

Writing out the integrand explicitly, we find
\begin{equation}\label{eqn:fundamentalTheoremOfGC:340}
\int_A^B F d^1\Bx \lrpartial G
=
\int_A^B \lr{
\PD{\alpha}{F} d\alpha\, \Bx_\alpha \Bx^\alpha G
+
F d\alpha\, \Bx_\alpha \Bx^\alpha \PD{\alpha}{G }
}
\end{equation}
However for a single parameter curve, we have \( \Bx^\alpha = 1/\Bx_\alpha \), so we are left with
\begin{equation}\label{eqn:fundamentalTheoremOfGC:360}
\begin{aligned}
\int_A^B F d^1\Bx \lrpartial G
&=
\int_A^B d\alpha\, \PD{\alpha}{(F G)} \\
&=
\evalbar{F G}{B}
–
\evalbar{F G}{A}.
\end{aligned}
\end{equation}

End proof.

More to come.

In the next installment we will explore surface integrals in spacetime, and the generalization of the fundamental theorem to multivector space time integrals.

References

[1] Peeter Joot. Geometric Algebra for Electrical Engineers. Kindle Direct Publishing, 2019.

[2] A. Macdonald. Vector and Geometric Calculus. CreateSpace Independent Publishing Platform, 2012.

A couple more reciprocal frame examples.

December 14, 2020 math and physics play , , , , , , , , , , , , ,

[If mathjax doesn’t display properly for you, click here for a PDF of this post]

This post logically follows both of the following:

  1. Curvilinear coordinates and gradient in spacetime, and reciprocal frames, and
  2. Lorentz transformations in Space Time Algebra (STA)

The PDF linked above above contains all the content from this post plus (1.) above [to be edited later into a more logical sequence.]

More examples.

Here are a few additional examples of reciprocal frame calculations.

Problem: Unidirectional arbitrary functional dependence.

Let
\begin{equation}\label{eqn:reciprocal:2540}
x = a f(u),
\end{equation}
where \( a \) is a constant vector and \( f(u)\) is some arbitrary differentiable function with a non-zero derivative in the region of interest.

Answer

Here we have just a single tangent space direction (a line in spacetime) with tangent vector
\begin{equation}\label{eqn:reciprocal:2400}
\Bx_u = a \PD{u}{f} = a f_u,
\end{equation}
so we see that the tangent space vectors are just rescaled values of the direction vector \( a \).
This is a simple enough parameterization that we can compute the reciprocal frame vector explicitly using the gradient. We expect that \( \Bx^u = 1/\Bx_u \), and find
\begin{equation}\label{eqn:reciprocal:2420}
\inv{a} \cdot x = f(u),
\end{equation}
but for constant \( a \), we know that \( \grad a \cdot x = a \), so taking gradients of both sides we find
\begin{equation}\label{eqn:reciprocal:2440}
\inv{a} = \grad f = \PD{u}{f} \grad u,
\end{equation}
so the reciprocal vector is
\begin{equation}\label{eqn:reciprocal:2460}
\Bx^u = \grad u = \inv{a f_u},
\end{equation}
as expected.

Problem: Linear two variable parameterization.

Let \( x = a u + b v \), where \( x \wedge a \wedge b = 0 \) represents spacetime plane (also the tangent space.) Find the curvilinear coordinates and their reciprocals.

Answer

The frame vectors are easy to compute, as they are just
\begin{equation}\label{eqn:reciprocal:1960}
\begin{aligned}
\Bx_u &= \PD{u}{x} = a \\
\Bx_v &= \PD{v}{x} = b.
\end{aligned}
\end{equation}
This is an example of a parametric equation that we can easily invert, as we have
\begin{equation}\label{eqn:reciprocal:1980}
\begin{aligned}
x \wedge a &= – v \lr{ a \wedge b } \\
x \wedge b &= u \lr{ a \wedge b },
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:reciprocal:2000}
\begin{aligned}
u
&= \inv{ a \wedge b } \cdot \lr{ x \wedge b } \\
&= \inv{ \lr{a \wedge b}^2 } \lr{ a \wedge b } \cdot \lr{ x \wedge b } \\
&=
\frac{
\lr{b \cdot x} \lr{ a \cdot b }
–
\lr{a \cdot x} \lr{ b \cdot b }
}{ \lr{a \wedge b}^2 }
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:reciprocal:2020}
\begin{aligned}
v &= -\inv{ a \wedge b } \cdot \lr{ x \wedge a } \\
&= -\inv{ \lr{a \wedge b}^2 } \lr{ a \wedge b } \cdot \lr{ x \wedge a } \\
&=
-\frac{
\lr{b \cdot x} \lr{ a \cdot a }
–
\lr{a \cdot x} \lr{ a \cdot b }
}{ \lr{a \wedge b}^2 }
\end{aligned}
\end{equation}
Recall that \( \grad \lr{ a \cdot x} = a \), if \( a \) is a constant, so our gradients are just
\begin{equation}\label{eqn:reciprocal:2040}
\begin{aligned}
\grad u
&=
\frac{
b \lr{ a \cdot b }
–
a
\lr{ b \cdot b }
}{ \lr{a \wedge b}^2 } \\
&=
b \cdot \inv{ a \wedge b },
\end{aligned}
\end{equation}
and
\begin{equation}\label{eqn:reciprocal:2060}
\begin{aligned}
\grad v
&=
-\frac{
b \lr{ a \cdot a }
–
a \lr{ a \cdot b }
}{ \lr{a \wedge b}^2 } \\
&=
-a \cdot \inv{ a \wedge b }.
\end{aligned}
\end{equation}
Expressed in terms of the frame vectors, this is just
\begin{equation}\label{eqn:reciprocal:2080}
\begin{aligned}
\Bx^u &= \Bx_v \cdot \inv{ \Bx_u \wedge \Bx_v } \\
\Bx^v &= -\Bx_u \cdot \inv{ \Bx_u \wedge \Bx_v },
\end{aligned}
\end{equation}
so we were able to show, for this special two parameter linear case, that the explicit evaluation of the gradients has the exact structure that we intuited that the reciprocals must have, provided they are constrained to the spacetime plane \( a \wedge b \). It is interesting to observe how this structure falls out of the linear system solution so directly. Also note that these reciprocals are not defined at the origin of the \( (u,v) \) parameter space.

Problem: Quadratic two variable parameterization.

Now consider a variation of the previous problem, with \( x = a u^2 + b v^2 \). Find the curvilinear coordinates and their reciprocals.

Answer

\begin{equation}\label{eqn:reciprocal:2100}
\begin{aligned}
\Bx_u &= \PD{u}{x} = 2 u a \\
\Bx_v &= \PD{v}{x} = 2 v b.
\end{aligned}
\end{equation}
Our tangent space is still the \( a \wedge b \) plane (as is the surface itself), but the spacing of the cells starts getting wider in proportion to \( u, v \).
Utilizing the work from the previous problem, we have
\begin{equation}\label{eqn:reciprocal:2120}
\begin{aligned}
2 u \grad u &=
b \cdot \inv{ a \wedge b } \\
2 v \grad v &=
-a \cdot \inv{ a \wedge b }.
\end{aligned}
\end{equation}
A bit of rearrangement can show that this is equivalent to the reciprocal frame identities. This is a second demonstration that the gradient and the algebraic formulations for the reciprocals match, at least for these special cases of linear non-coupled parameterizations.

Problem: Reciprocal frame for generalized cylindrical parameterization.

Let the vector parameterization be \( x(\rho,\theta) = \rho e^{-i\theta/2} x(\rho_0, \theta_0) e^{i \theta} \), where \( i^2 = \pm 1 \) is a unit bivector (\(+1\) for a boost, and \(-1\) for a rotation), and where \(\theta, \rho\) are scalars. Find the tangent space vectors and their reciprocals.

fig. 1. “Cylindrical” boost parameterization.

Note that this is cylindrical parameterization for the rotation case, and traces out hyperbolic regions for the boost case. The boost case is illustrated in fig. 1 where hyperbolas in the light cone are found for boosts of \( \gamma_0\) with various values of \(\rho\), and the spacelike hyperbolas are boosts of \( \gamma_1 \), again for various values of \( \rho \).

Answer

The tangent space vectors are
\begin{equation}\label{eqn:reciprocal:2480}
\Bx_\rho = \frac{x}{\rho},
\end{equation}
and

\begin{equation}\label{eqn:reciprocal:2500}
\begin{aligned}
\Bx_\theta
&= -\frac{i}{2} x + x \frac{i}{2} \\
&= x \cdot i.
\end{aligned}
\end{equation}
Recall that \( x \cdot i \) lies perpendicular to \( x \) (in the plane \( i \)), as illustrated in fig. 2. This means that \( \Bx_\rho \) and \( \Bx_\theta \) are orthogonal, so we can find the reciprocal vectors by just inverting them
\begin{equation}\label{eqn:reciprocal:2520}
\begin{aligned}
\Bx^\rho &= \frac{\rho}{x} \\
\Bx^\theta &= \frac{1}{x \cdot i}.
\end{aligned}
\end{equation}

fig. 2. Projection and rejection geometry.

Parameterization of a general linear transformation.

Given \( N \) parameters \( u^0, u^1, \cdots u^{N-1} \), a general linear transformation from the parameter space to the vector space has the form
\begin{equation}\label{eqn:reciprocal:2160}
x =
{a^\alpha}_\beta \gamma_\alpha u^\beta,
\end{equation}
where \( \beta \in [0, \cdots, N-1] \) and \( \alpha \in [0,3] \).
For such a general transformation, observe that the curvilinear basis vectors are
\begin{equation}\label{eqn:reciprocal:2180}
\begin{aligned}
\Bx_\mu
&= \PD{u^\mu}{x} \\
&= \PD{u^\mu}{}
{a^\alpha}_\beta \gamma_\alpha u^\beta \\
&=
{a^\alpha}_\mu \gamma_\alpha.
\end{aligned}
\end{equation}
We find an interpretation of \( {a^\alpha}_\mu \) by dotting \( \Bx_\mu \) with the reciprocal frame vectors of the standard basis
\begin{equation}\label{eqn:reciprocal:2200}
\begin{aligned}
\Bx_\mu \cdot \gamma^\nu
&=
{a^\alpha}_\mu \lr{ \gamma_\alpha \cdot \gamma^\nu } \\
&=
{a^\nu}_\mu,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:reciprocal:2220}
x = \Bx_\mu u^\mu.
\end{equation}
We are able to reinterpret \ref{eqn:reciprocal:2160} as a contraction of the tangent space vectors with the parameters, scaling and summing these direction vectors to characterize all the points in the tangent plane.

Theorem 1.1: Projecting onto the tangent space.

Let \( T \) represent the tangent space. The projection of a vector onto the tangent space has the form
\begin{equation}\label{eqn:reciprocal:2560}
\textrm{Proj}_{\textrm{T}} y = \lr{ y \cdot \Bx^\mu } \Bx_\mu = \lr{ y \cdot \Bx_\mu } \Bx^\mu.
\end{equation}

Start proof:

Let’s designate \( a \) as the portion of the vector \( y \) that lies outside of the tangent space
\begin{equation}\label{eqn:reciprocal:2260}
y = y^\mu \Bx_\mu + a.
\end{equation}
If we knew the coordinates \( y^\mu \), we would have a recipe for the projection.
Algebraically, requiring that \( a \) lies outside of the tangent space, is equivalent to stating \( a \cdot \Bx_\mu = a \cdot \Bx^\mu = 0 \). We use that fact, and then take dot products
\begin{equation}\label{eqn:reciprocal:2280}
\begin{aligned}
y \cdot \Bx^\nu
&= \lr{ y^\mu \Bx_\mu + a } \cdot \Bx^\nu \\
&= y^\nu,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:reciprocal:2300}
y = \lr{ y \cdot \Bx^\mu } \Bx_\mu + a.
\end{equation}
Similarly, the tangent space projection can be expressed as a linear combination of reciprocal basis elements
\begin{equation}\label{eqn:reciprocal:2320}
y = y_\mu \Bx^\mu + a.
\end{equation}
Dotting with \( \Bx_\mu \), we have
\begin{equation}\label{eqn:reciprocal:2340}
\begin{aligned}
y \cdot \Bx^\mu
&= \lr{ y_\alpha \Bx^\alpha + a } \cdot \Bx_\mu \\
&= y_\mu,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:reciprocal:2360}
y = \lr{ y \cdot \Bx^\mu } \Bx_\mu + a.
\end{equation}
We find the two stated ways of computing the projection.

Observe that, for the special case that all of \( \setlr{ \Bx_\mu } \) are orthogonal, the equivalence of these two projection methods follows directly, since
\begin{equation}\label{eqn:reciprocal:2380}
\begin{aligned}
\lr{ y \cdot \Bx^\mu } \Bx_\mu
&=
\lr{ y \cdot \inv{\Bx_\mu} } \inv{\Bx^\mu} \\
&=
\lr{ y \cdot \frac{\Bx_\mu}{\lr{\Bx_\mu}^2 } } \frac{\Bx^\mu}{\lr{\Bx^\mu}^2} \\
&=
\lr{ y \cdot \Bx_\mu } \Bx^\mu.
\end{aligned}
\end{equation}

End proof.