gradient

Vector gradients in dyadic notation and geometric algebra.

March 5, 2022 math and physics play , , , ,

[If mathjax doesn’t display properly for you, click here for a PDF of this post]

This is an exploration of the dyadic representation of the gradient acting on a vector in \(\mathbb{R}^3\), where we determine a tensor product formulation of a vector differential. Such a tensor product formulation can be split into symmetric and antisymmetric components. The geometric algebra (GA) equivalents of such a split are determined.

There is an error in part of the analysis below, which is addressed in a followup post made the next day.

GA gradient of a vector.

In GA we are free to express the product of the gradient and a vector field by adjacency. In coordinates (summation over repeated indexes assumed), such a product has the form
\begin{equation}\label{eqn:dyadicVsGa:20}
\spacegrad \Bv
= \lr{ \Be_i \partial_i } \lr{ v_j \Be_j }
= \lr{ \partial_i v_j } \Be_i \Be_j.
\end{equation}
In this sum, any terms with \( i = j \) are scalars since \( \Be_i^2 = 1 \), and the remaining terms are bivectors. This can be written compactly as
\begin{equation}\label{eqn:dyadicVsGa:40}
\spacegrad \Bv = \spacegrad \cdot \Bv + \spacegrad \wedge \Bv,
\end{equation}
or for \(\mathbb{R}^3\)
\begin{equation}\label{eqn:dyadicVsGa:60}
\spacegrad \Bv = \spacegrad \cdot \Bv + I \lr{ \spacegrad \cross \Bv},
\end{equation}
either of which breaks the gradient into into divergence and curl components. In \ref{eqn:dyadicVsGa:40} this vector gradient is expressed using the bivector valued curl operator \( (\spacegrad \wedge \Bv) \), whereas \ref{eqn:dyadicVsGa:60} is expressed using the vector valued dual form of the curl \( (\spacegrad \cross \Bv) \) from convential vector algebra.

It is worth noting that order matters in the GA coordinate expansion of \ref{eqn:dyadicVsGa:20}. It is not correct to write
\begin{equation}\label{eqn:dyadicVsGa:80}
\spacegrad \Bv
= \lr{ \partial_i v_j } \Be_j \Be_i,
\end{equation}
which is only true when the curl, \( \spacegrad \wedge \Bv = 0 \), is zero.

Dyadic representation.

Given a vector field \( \Bv = \Bv(\Bx) \), the differential of that field can be computed by chain rule
\begin{equation}\label{eqn:dyadicVsGa:100}
d\Bv = \PD{x_i}{\Bv} dx_i = \lr{ d\Bx \cdot \spacegrad} \Bv,
\end{equation}
where \( d\Bx = \Be_i dx_i \). This is a representation invariant form of the differential, where we have a scalar operator \( d\Bx \cdot \spacegrad \) acting on the vector field \( \Bv \). The matrix representation of this differential can be written as
\begin{equation}\label{eqn:dyadicVsGa:120}
d\Bv = \lr{
{\begin{bmatrix}
d\Bx
\end{bmatrix}}^\dagger
\begin{bmatrix}
\spacegrad
\end{bmatrix}
}
\begin{bmatrix}
\Bv
\end{bmatrix}
,
\end{equation}
where we are using the dagger to designate transposition, and each of the terms on the right are the coordinate matrixes of the vectors with respect to the standard basis
\begin{equation}\label{eqn:dyadicVsGa:140}
\begin{bmatrix}
d\Bx
\end{bmatrix}
=
\begin{bmatrix}
dx_1 \\
dx_2 \\
dx_3
\end{bmatrix},\quad
\begin{bmatrix}
\Bv
\end{bmatrix}
=
\begin{bmatrix}
v_1 \\
v_2 \\
v_3
\end{bmatrix},\quad
\begin{bmatrix}
\spacegrad
\end{bmatrix}
=
\begin{bmatrix}
\partial_1 \\
\partial_2 \\
\partial_3
\end{bmatrix}.
\end{equation}

In \ref{eqn:dyadicVsGa:120} the parens are very important, as the expression is meaningless without them. With the parens we have a \((1 \times 3)(3 \times 1)\) matrix (i.e. a scalar) multiplied with a \(3\times 1\) matrix. That becomes ill-formed if we drop the parens since we are left with an incompatible product of a \((3\times1)(3\times1)\) matrix on the right. The dyadic notation, which introducing a tensor product into the mix, is a mechanism to make sense of the possibility of such a product. Can we make sense of an expression like \( \spacegrad \Bv \) without the geometric product in our toolbox?

Stepping towards that question, let’s examine the coordinate expansion of our vector differential \ref{eqn:dyadicVsGa:100}, which is
\begin{equation}\label{eqn:dyadicVsGa:160}
d\Bv = dx_i \lr{ \partial_i v_j } \Be_j.
\end{equation}
If we allow a matrix of vectors, this has a block matrix form
\begin{equation}\label{eqn:dyadicVsGa:180}
d\Bv =
{\begin{bmatrix}
d\Bx
\end{bmatrix}}^\dagger
\begin{bmatrix}
\spacegrad \otimes \Bv
\end{bmatrix}
\begin{bmatrix}
\Be_1 \\
\Be_2 \\
\Be_3
\end{bmatrix}
.
\end{equation}
Here we introduce the tensor product
\begin{equation}\label{eqn:dyadicVsGa:200}
\spacegrad \otimes \Bv
= \partial_i v_j \, \Be_i \otimes \Be_j,
\end{equation}
and designate the matrix of coordinates \( \partial_i v_j \), a second order tensor, by \(
\begin{bmatrix}
\spacegrad \otimes \Bv
\end{bmatrix}
\).

We have succeeded in factoring out a vector gradient. We can introduce dot product between vectors and a direct product of vectors, by observing that \ref{eqn:dyadicVsGa:180} has the structure of a quadradic form, and define
\begin{equation}\label{eqn:dyadicVsGa:220}
\Bx \cdot (\Ba \otimes \Bb) \equiv
{\begin{bmatrix}
\Bx
\end{bmatrix}}^\dagger
\begin{bmatrix}
\Ba \otimes \Bb
\end{bmatrix}
\begin{bmatrix}
\Be_1 \\
\Be_2 \\
\Be_3
\end{bmatrix},
\end{equation}
so that \ref{eqn:dyadicVsGa:180} takes the form
\begin{equation}\label{eqn:dyadicVsGa:240}
d\Bv = d\Bx \cdot \lr{ \spacegrad \otimes \Bv }.
\end{equation}
Such a dot product gives operational meaning to the gradient-vector tensor product.

Symmetrization and antisymmetrization of the vector differential in GA.

Using the dyadic notation, it’s possible to split a vector derivative into symmetric and antisymmetric components with respect to the gradient-vector direct product
\begin{equation}\label{eqn:dyadicVsGa:260}
d\Bv
= d\Bx \cdot
\lr{
\inv{2} \lr{ \spacegrad \otimes \Bv + \lr{ \spacegrad \otimes \Bv }^\dagger }
+
\inv{2} \lr{ \spacegrad \otimes \Bv – \lr{ \spacegrad \otimes \Bv }^\dagger }
},
\end{equation}
or \( d\Bv = d\Bx \cdot \lr{ \Bd + \BOmega } \), where \( \Bd \) is a symmetric tensor, and \( \BOmega \) is a traceless antisymmetric tensor.

A question of potential interest is “what GA equvivalent of this expression?”. There are two identities that are helpful for extracting this equivalence, the first of which is the k-blade vector product identities. Given a k-blade \( B_k \) (i.e.: a product of \( k \) orthogonal vectors, or the wedge of \( k \) vectors), and a vector \( \Ba \), the dot product of the two is
\begin{equation}\label{eqn:dyadicVsGa:280}
B_k \cdot \Ba = \inv{2} \lr{ B_k \Ba + (-1)^{k+1} \Ba B_k }
\end{equation}
Specifically, given two vectors \( \Ba, \Bb \), the vector dot product can be written as a symmetric sum
\begin{equation}\label{eqn:dyadicVsGa:300}
\Ba \cdot \Bb = \inv{2} \lr{ \Ba \Bb + \Bb \Ba } = \Bb \cdot \Ba,
\end{equation}
and given a bivector \( B \) and a vector \( \Ba \), the bivector-vector dot product can be written as an antisymmetric sum
\begin{equation}\label{eqn:dyadicVsGa:320}
B \cdot \Ba = \inv{2} \lr{ B \Ba – \Ba B } = – \Ba \cdot B.
\end{equation}

We may apply these to expressions where one of the vector terms is the gradient, but must allow for the gradient to act bidirectionally. That is, given multivectors \( M, N \)
\begin{equation}\label{eqn:dyadicVsGa:340}
M \spacegrad N
=
\partial_i (M \Be_i N)
=
(\partial_i M) \Be_i N + M \Be_i (\partial_i N),
\end{equation}
where parens have been used to indicate the scope of applicibility of the partials. In particular, this means that we may write the divergence as a GA symmetric sum
\begin{equation}\label{eqn:dyadicVsGa:360}
\spacegrad \cdot \Bv = \inv{2} \lr{
\spacegrad \Bv + \Bv \spacegrad },
\end{equation}
which clearly corresponds to the symmetric term \( \Bd = (1/2) \lr{ \spacegrad \otimes \Bv + \lr{ \spacegrad \otimes \Bv }^\dagger } \) from \ref{eqn:dyadicVsGa:260}.

Let’s assume that we can write our vector differential in terms of a divergence term isomorphic to the symmetric sum in \ref{eqn:dyadicVsGa:260}, and a “something else”, \(\BX\). That is
\begin{equation}\label{eqn:dyadicVsGa:380}
\begin{aligned}
d\Bv
&= \lr{ d\Bx \cdot \spacegrad } \Bv \\
&= d\Bx (\spacegrad \cdot \Bv) + \BX,
\end{aligned}
\end{equation}
where
\begin{equation}\label{eqn:dyadicVsGa:400}
\BX = \lr{ d\Bx \cdot \spacegrad } \Bv – d\Bx (\spacegrad \cdot \Bv),
\end{equation}
is a vector expression to be reduced to something simpler. That reduction is possible using the distribution identity
\begin{equation}\label{eqn:dyadicVsGa:420}
\Bc \cdot (\Ba \wedge \Bb)
=
(\Bc \cdot \Ba) \Bb
– (\Bc \cdot \Bb) \Ba,
\end{equation}
so we find
\begin{equation}\label{eqn:dyadicVsGa:440}
\BX = \spacegrad \cdot \lr{ d\Bx \wedge \Bv }.
\end{equation}

We find the following GA split of the vector differential into symmetric and antisymmetric terms
\begin{equation}\label{eqn:dyadicVsGa:460}
\boxed{
d\Bv
= (d\Bx \cdot \spacegrad) \Bv
= d\Bx (\spacegrad \cdot \Bv)
+
\spacegrad \cdot \lr{ d\Bx \wedge \Bv }.
}
\end{equation}
Such a split avoids the indeterminant nature of the tensor product, which we only give meaning by introducing the quadratic form based dot product given by \ref{eqn:dyadicVsGa:220}.

Unpacking the fundamental theorem of multivector calculus in two dimensions

January 18, 2021 math and physics play , , , , , , , , , , , , , , , , , , ,

Notes.

Due to limitations in the MathJax-Latex package, all the oriented integrals in this blog post should be interpreted as having a clockwise orientation. [See the PDF version of this post for more sophisticated formatting.]

Guts.

Given a two dimensional generating vector space, there are two instances of the fundamental theorem for multivector integration
\begin{equation}\label{eqn:unpackingFundamentalTheorem:20}
\int_S F d\Bx \lrpartial G = \evalbar{F G}{\Delta S},
\end{equation}
and
\begin{equation}\label{eqn:unpackingFundamentalTheorem:40}
\int_S F d^2\Bx \lrpartial G = \oint_{\partial S} F d\Bx G.
\end{equation}
The first case is trivial. Given a parameterizated curve \( x = x(u) \), it just states
\begin{equation}\label{eqn:unpackingFundamentalTheorem:60}
\int_{u(0)}^{u(1)} du \PD{u}{}\lr{FG} = F(u(1))G(u(1)) – F(u(0))G(u(0)),
\end{equation}
for all multivectors \( F, G\), regardless of the signature of the underlying space.

The surface integral is more interesting. Let’s first look at the area element for this surface integral, which is
\begin{equation}\label{eqn:unpackingFundamentalTheorem:80}
d^2 \Bx = d\Bx_u \wedge d \Bx_v.
\end{equation}
Geometrically, this has the area of the parallelogram spanned by \( d\Bx_u \) and \( d\Bx_v \), but weighted by the pseudoscalar of the space. This is explored algebraically in the following problem and illustrated in fig. 1.

fig. 1. 2D vector space and area element.

Problem: Expansion of 2D area bivector.

Let \( \setlr{e_1, e_2} \) be an orthonormal basis for a two dimensional space, with reciprocal frame \( \setlr{e^1, e^2} \). Expand the area bivector \( d^2 \Bx \) in coordinates relating the bivector to the Jacobian and the pseudoscalar.

Answer

With parameterization \( x = x(u,v) = x^\alpha e_\alpha = x_\alpha e^\alpha \), we have
\begin{equation}\label{eqn:unpackingFundamentalTheorem:120}
\Bx_u \wedge \Bx_v
=
\lr{ \PD{u}{x^\alpha} e_\alpha } \wedge
\lr{ \PD{v}{x^\beta} e_\beta }
=
\PD{u}{x^\alpha}
\PD{v}{x^\beta}
e_\alpha
e_\beta
=
\PD{(u,v)}{(x^1,x^2)} e_1 e_2,
\end{equation}
or
\begin{equation}\label{eqn:unpackingFundamentalTheorem:160}
\Bx_u \wedge \Bx_v
=
\lr{ \PD{u}{x_\alpha} e^\alpha } \wedge
\lr{ \PD{v}{x_\beta} e^\beta }
=
\PD{u}{x_\alpha}
\PD{v}{x_\beta}
e^\alpha
e^\beta
=
\PD{(u,v)}{(x_1,x_2)} e^1 e^2.
\end{equation}
The upper and lower index pseudoscalars are related by
\begin{equation}\label{eqn:unpackingFundamentalTheorem:180}
e^1 e^2 e_1 e_2 =
-e^1 e^2 e_2 e_1 =
-1,
\end{equation}
so with \( I = e_1 e_2 \),
\begin{equation}\label{eqn:unpackingFundamentalTheorem:200}
e^1 e^2 = -I^{-1},
\end{equation}
leaving us with
\begin{equation}\label{eqn:unpackingFundamentalTheorem:140}
d^2 \Bx
= \PD{(u,v)}{(x^1,x^2)} du dv\, I
= -\PD{(u,v)}{(x_1,x_2)} du dv\, I^{-1}.
\end{equation}
We see that the area bivector is proportional to either the upper or lower index Jacobian and to the pseudoscalar for the space.

We may write the fundamental theorem for a 2D space as
\begin{equation}\label{eqn:unpackingFundamentalTheorem:680}
\int_S du dv \, \PD{(u,v)}{(x^1,x^2)} F I \lrgrad G = \oint_{\partial S} F d\Bx G,
\end{equation}
where we have dispensed with the vector derivative and use the gradient instead, since they are identical in a two parameter two dimensional space. Of course, unless we are using \( x^1, x^2 \) as our parameterization, we still want the curvilinear representation of the gradient \( \grad = \Bx^u \PDi{u}{} + \Bx^v \PDi{v}{} \).

Problem: Standard basis expansion of fundamental surface relation.

For a parameterization \( x = x^1 e_1 + x^2 e_2 \), where \( \setlr{ e_1, e_2 } \) is a standard (orthogonal) basis, expand the fundamental theorem for surface integrals for the single sided \( F = 1 \) case. Consider functions \( G \) of each grade (scalar, vector, bivector.)

Answer

From \ref{eqn:unpackingFundamentalTheorem:140} we see that the fundamental theorem takes the form
\begin{equation}\label{eqn:unpackingFundamentalTheorem:220}
\int_S dx^1 dx^2\, F I \lrgrad G = \oint_{\partial S} F d\Bx G.
\end{equation}
In a Euclidean space, the operator \( I \lrgrad \), is a \( \pi/2 \) rotation of the gradient, but has a rotated like structure in all metrics:
\begin{equation}\label{eqn:unpackingFundamentalTheorem:240}
I \grad
=
e_1 e_2 \lr{ e^1 \partial_1 + e^2 \partial_2 }
=
-e_2 \partial_1 + e_1 \partial_2.
\end{equation}

  • \( F = 1 \) and \( G \in \bigwedge^0 \) or \( G \in \bigwedge^2 \). For \( F = 1 \) and scalar or bivector \( G \) we have
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:260}
    \int_S dx^1 dx^2\, \lr{ -e_2 \partial_1 + e_1 \partial_2 } G = \oint_{\partial S} d\Bx G,
    \end{equation}
    where, for \( x^1 \in [x^1(0),x^1(1)] \) and \( x^2 \in [x^2(0),x^2(1)] \), the RHS written explicitly is
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:280}
    \oint_{\partial S} d\Bx G
    =
    \int dx^1 e_1
    \lr{ G(x^1, x^2(1)) – G(x^1, x^2(0)) }
    – dx^2 e_2
    \lr{ G(x^1(1),x^2) – G(x^1(0), x^2) }.
    \end{equation}
    This is sketched in fig. 2. Since a 2D bivector \( G \) can be written as \( G = I g \), where \( g \) is a scalar, we may write the pseudoscalar case as
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:300}
    \int_S dx^1 dx^2\, \lr{ -e_2 \partial_1 + e_1 \partial_2 } g = \oint_{\partial S} d\Bx g,
    \end{equation}
    after right multiplying both sides with \( I^{-1} \). Algebraically the scalar and pseudoscalar cases can be thought of as identical scalar relationships.
  • \( F = 1, G \in \bigwedge^1 \). For \( F = 1 \) and vector \( G \) the 2D fundamental theorem for surfaces can be split into scalar
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:320}
    \int_S dx^1 dx^2\, \lr{ -e_2 \partial_1 + e_1 \partial_2 } \cdot G = \oint_{\partial S} d\Bx \cdot G,
    \end{equation}
    and bivector relations
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:340}
    \int_S dx^1 dx^2\, \lr{ -e_2 \partial_1 + e_1 \partial_2 } \wedge G = \oint_{\partial S} d\Bx \wedge G.
    \end{equation}
    To expand \ref{eqn:unpackingFundamentalTheorem:320}, let
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:360}
    G = g_1 e^1 + g_2 e^2,
    \end{equation}
    for which
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:380}
    \lr{ -e_2 \partial_1 + e_1 \partial_2 } \cdot G
    =
    \lr{ -e_2 \partial_1 + e_1 \partial_2 } \cdot
    \lr{ g_1 e^1 + g_2 e^2 }
    =
    \partial_2 g_1 – \partial_1 g_2,
    \end{equation}
    and
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:400}
    d\Bx \cdot G
    =
    \lr{ dx^1 e_1 – dx^2 e_2 } \cdot \lr{ g_1 e^1 + g_2 e^2 }
    =
    dx^1 g_1 – dx^2 g_2,
    \end{equation}
    so \ref{eqn:unpackingFundamentalTheorem:320} expands to
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:500}
    \int_S dx^1 dx^2\, \lr{ \partial_2 g_1 – \partial_1 g_2 }
    =
    \int
    \evalbar{dx^1 g_1}{\Delta x^2} – \evalbar{ dx^2 g_2 }{\Delta x^1}.
    \end{equation}
    This coordinate expansion illustrates how the pseudoscalar nature of the area element results in a duality transformation, as we end up with a curl like operation on the LHS, despite the dot product nature of the decomposition that we used. That can also be seen directly for vector \( G \), since
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:560}
    dA (I \grad) \cdot G
    =
    dA \gpgradezero{ I \grad G }
    =
    dA I \lr{ \grad \wedge G },
    \end{equation}
    since the scalar selection of \( I \lr{ \grad \cdot G } \) is zero.In the grade-2 relation \ref{eqn:unpackingFundamentalTheorem:340}, we expect a pseudoscalar cancellation on both sides, leaving a scalar (divergence-like) relationship. This time, we use upper index coordinates for the vector \( G \), letting
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:440}
    G = g^1 e_1 + g^2 e_2,
    \end{equation}
    so
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:460}
    \lr{ -e_2 \partial_1 + e_1 \partial_2 } \wedge G
    =
    \lr{ -e_2 \partial_1 + e_1 \partial_2 } \wedge G
    \lr{ g^1 e_1 + g^2 e_2 }
    =
    e_1 e_2 \lr{ \partial_1 g^1 + \partial_2 g^2 },
    \end{equation}
    and
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:480}
    d\Bx \wedge G
    =
    \lr{ dx^1 e_1 – dx^2 e_2 } \wedge
    \lr{ g^1 e_1 + g^2 e_2 }
    =
    e_1 e_2 \lr{ dx^1 g^2 + dx^2 g^1 }.
    \end{equation}
    So \ref{eqn:unpackingFundamentalTheorem:340}, after multiplication of both sides by \( I^{-1} \), is
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:520}
    \int_S dx^1 dx^2\,
    \lr{ \partial_1 g^1 + \partial_2 g^2 }
    =
    \int
    \evalbar{dx^1 g^2}{\Delta x^2} + \evalbar{dx^2 g^1 }{\Delta x^1}.
    \end{equation}

As before, we’ve implicitly performed a duality transformation, and end up with a divergence operation. That can be seen directly without coordinate expansion, by rewriting the wedge as a grade two selection, and expanding the gradient action on the vector \( G \), as follows
\begin{equation}\label{eqn:unpackingFundamentalTheorem:580}
dA (I \grad) \wedge G
=
dA \gpgradetwo{ I \grad G }
=
dA I \lr{ \grad \cdot G },
\end{equation}
since \( I \lr{ \grad \wedge G } \) has only a scalar component.

 

fig. 2. Line integral around rectangular boundary.

Theorem 1.1: Green’s theorem [1].

Let \( S \) be a Jordan region with a piecewise-smooth boundary \( C \). If \( P, Q \) are continuously differentiable on an open set that contains \( S \), then
\begin{equation*}
\int dx dy \lr{ \PD{y}{P} – \PD{x}{Q} } = \oint P dx + Q dy.
\end{equation*}

Problem: Relationship to Green’s theorem.

If the space is Euclidean, show that \ref{eqn:unpackingFundamentalTheorem:500} and \ref{eqn:unpackingFundamentalTheorem:520} are both instances of Green’s theorem with suitable choices of \( P \) and \( Q \).

Answer

I will omit the subtleties related to general regions and consider just the case of an infinitesimal square region.

Start proof:

Let’s start with \ref{eqn:unpackingFundamentalTheorem:500}, with \( g_1 = P \) and \( g_2 = Q \), and \( x^1 = x, x^2 = y \), the RHS is
\begin{equation}\label{eqn:unpackingFundamentalTheorem:600}
\int dx dy \lr{ \PD{y}{P} – \PD{x}{Q} }.
\end{equation}
On the RHS we have
\begin{equation}\label{eqn:unpackingFundamentalTheorem:620}
\int \evalbar{dx P}{\Delta y} – \evalbar{ dy Q }{\Delta x}
=
\int dx \lr{ P(x, y_1) – P(x, y_0) } – \int dy \lr{ Q(x_1, y) – Q(x_0, y) }.
\end{equation}
This pair of integrals is plotted in fig. 3, from which we see that \ref{eqn:unpackingFundamentalTheorem:620} can be expressed as the line integral, leaving us with
\begin{equation}\label{eqn:unpackingFundamentalTheorem:640}
\int dx dy \lr{ \PD{y}{P} – \PD{x}{Q} }
=
\oint dx P + dy Q,
\end{equation}
which is Green’s theorem over the infinitesimal square integration region.

For the equivalence of \ref{eqn:unpackingFundamentalTheorem:520} to Green’s theorem, let \( g^2 = P \), and \( g^1 = -Q \). Plugging into the LHS, we find the Green’s theorem integrand. On the RHS, the integrand expands to
\begin{equation}\label{eqn:unpackingFundamentalTheorem:660}
\evalbar{dx g^2}{\Delta y} + \evalbar{dy g^1 }{\Delta x}
=
dx \lr{ P(x,y_1) – P(x, y_0)}
+
dy \lr{ -Q(x_1, y) + Q(x_0, y)},
\end{equation}
which is exactly what we found in \ref{eqn:unpackingFundamentalTheorem:620}.

End proof.

 

fig. 3. Path for Green’s theorem.

We may also relate multivector gradient integrals in 2D to the normal integral around the boundary of the bounding curve. That relationship is as follows.

Theorem 1.2: 2D gradient integrals.

\begin{equation*}
\begin{aligned}
\int J du dv \rgrad G &= \oint I^{-1} d\Bx G = \int J \lr{ \Bx^v du + \Bx^u dv } G \\
\int J du dv F \lgrad &= \oint F I^{-1} d\Bx = \int J F \lr{ \Bx^v du + \Bx^u dv },
\end{aligned}
\end{equation*}
where \( J = \partial(x^1, x^2)/\partial(u,v) \) is the Jacobian of the parameterization \( x = x(u,v) \). In terms of the coordinates \( x^1, x^2 \), this reduces to
\begin{equation*}
\begin{aligned}
\int dx^1 dx^2 \rgrad G &= \oint I^{-1} d\Bx G = \int \lr{ e^2 dx^1 + e^1 dx^2 } G \\
\int dx^1 dx^2 F \lgrad &= \oint G I^{-1} d\Bx = \int F \lr{ e^2 dx^1 + e^1 dx^2 }.
\end{aligned}
\end{equation*}
The vector \( I^{-1} d\Bx \) is orthogonal to the tangent vector along the boundary, and for Euclidean spaces it can be identified as the outwards normal.

Start proof:

Respectively setting \( F = 1 \), and \( G = 1\) in \ref{eqn:unpackingFundamentalTheorem:680}, we have
\begin{equation}\label{eqn:unpackingFundamentalTheorem:940}
\int I^{-1} d^2 \Bx \rgrad G = \oint I^{-1} d\Bx G,
\end{equation}
and
\begin{equation}\label{eqn:unpackingFundamentalTheorem:960}
\int F d^2 \Bx \lgrad I^{-1} = \oint F d\Bx I^{-1}.
\end{equation}
Starting with \ref{eqn:unpackingFundamentalTheorem:940} we find
\begin{equation}\label{eqn:unpackingFundamentalTheorem:700}
\int I^{-1} J du dv I \rgrad G = \oint d\Bx G,
\end{equation}
to find \( \int dx^1 dx^2 \rgrad G = \oint I^{-1} d\Bx G \), as desireed. In terms of a parameterization \( x = x(u,v) \), the pseudoscalar for the space is
\begin{equation}\label{eqn:unpackingFundamentalTheorem:720}
I = \frac{\Bx_u \wedge \Bx_v}{J},
\end{equation}
so
\begin{equation}\label{eqn:unpackingFundamentalTheorem:740}
I^{-1} = \frac{J}{\Bx_u \wedge \Bx_v}.
\end{equation}
Also note that \( \lr{\Bx_u \wedge \Bx_v}^{-1} = \Bx^v \wedge \Bx^u \), so
\begin{equation}\label{eqn:unpackingFundamentalTheorem:760}
I^{-1} = J \lr{ \Bx^v \wedge \Bx^u },
\end{equation}
and
\begin{equation}\label{eqn:unpackingFundamentalTheorem:780}
I^{-1} d\Bx
= I^{-1} \cdot d\Bx
= J \lr{ \Bx^v \wedge \Bx^u } \cdot \lr{ \Bx_u du – \Bx_v dv }
= J \lr{ \Bx^v du + \Bx^u dv },
\end{equation}
so the right acting gradient integral is
\begin{equation}\label{eqn:unpackingFundamentalTheorem:800}
\int J du dv \grad G =
\int
\evalbar{J \Bx^v G}{\Delta v} du + \evalbar{J \Bx^u G dv}{\Delta u},
\end{equation}
which we write in abbreviated form as \( \int J \lr{ \Bx^v du + \Bx^u dv} G \).

For the \( G = 1 \) case, from \ref{eqn:unpackingFundamentalTheorem:960} we find
\begin{equation}\label{eqn:unpackingFundamentalTheorem:820}
\int J du dv F I \lgrad I^{-1} = \oint F d\Bx I^{-1}.
\end{equation}
However, in a 2D space, regardless of metric, we have \( I a = – a I \) for any vector \( a \) (i.e. \( \grad \) or \( d\Bx\)), so we may commute the outer pseudoscalars in
\begin{equation}\label{eqn:unpackingFundamentalTheorem:840}
\int J du dv F I \lgrad I^{-1} = \oint F d\Bx I^{-1},
\end{equation}
so
\begin{equation}\label{eqn:unpackingFundamentalTheorem:850}
-\int J du dv F I I^{-1} \lgrad = -\oint F I^{-1} d\Bx.
\end{equation}
After cancelling the negative sign on both sides, we have the claimed result.

To see that \( I a \), for any vector \( a \) is normal to \( a \), we can compute the dot product
\begin{equation}\label{eqn:unpackingFundamentalTheorem:860}
\lr{ I a } \cdot a
=
\gpgradezero{ I a a }
=
a^2 \gpgradezero{ I }
= 0,
\end{equation}
since the scalar selection of a bivector is zero. Since \( I^{-1} = \pm I \), the same argument shows that \( I^{-1} d\Bx \) must be orthogonal to \( d\Bx \).

End proof.

Let’s look at the geometry of the normal \( I^{-1} \Bx \) in a couple 2D vector spaces. We use an integration volume of a unit square to simplify the boundary term expressions.

  • Euclidean: With a parameterization \( x(u,v) = u\Be_1 + v \Be_2 \), and Euclidean basis vectors \( (\Be_1)^2 = (\Be_2)^2 = 1 \), the fundamental theorem integrated over the rectangle \( [x_0,x_1] \times [y_0,y_1] \) is
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:880}
    \int dx dy \grad G =
    \int
    \Be_2 \lr{ G(x,y_1) – G(x,y_0) } dx +
    \Be_1 \lr{ G(x_1,y) – G(x_0,y) } dy,
    \end{equation}
    Each of the terms in the integrand above are illustrated in fig. 4, and we see that this is a path integral weighted by the outwards normal.

    fig. 4. Outwards oriented normal for Euclidean space.

  • Spacetime: Let \( x(u,v) = u \gamma_0 + v \gamma_1 \), where \( (\gamma_0)^2 = -(\gamma_1)^2 = 1 \). With \( u = t, v = x \), the gradient integral over a \([t_0,t_1] \times [x_0,x_1]\) of spacetime is
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:900}
    \begin{aligned}
    \int dt dx \grad G
    &=
    \int
    \gamma^1 dt \lr{ G(t, x_1) – G(t, x_0) }
    +
    \gamma^0 dx \lr{ G(t_1, x) – G(t_1, x) } \\
    &=
    \int
    \gamma_1 dt \lr{ -G(t, x_1) + G(t, x_0) }
    +
    \gamma_0 dx \lr{ G(t_1, x) – G(t_1, x) }
    .
    \end{aligned}
    \end{equation}
    With \( t \) plotted along the horizontal axis, and \( x \) along the vertical, each of the terms of this integrand is illustrated graphically in fig. 5. For this mixed signature space, there is no longer any good geometrical characterization of the normal.

    fig. 5. Orientation of the boundary normal for a spacetime basis.

  • Spacelike:
    Let \( x(u,v) = u \gamma_1 + v \gamma_2 \), where \( (\gamma_1)^2 = (\gamma_2)^2 = -1 \). With \( u = x, v = y \), the gradient integral over a \([x_0,x_1] \times [y_0,y_1]\) of this space is
    \begin{equation}\label{eqn:unpackingFundamentalTheorem:920}
    \begin{aligned}
    \int dx dy \grad G
    &=
    \int
    \gamma^2 dx \lr{ G(x, y_1) – G(x, y_0) }
    +
    \gamma^1 dy \lr{ G(x_1, y) – G(x_1, y) } \\
    &=
    \int
    \gamma_2 dx \lr{ -G(x, y_1) + G(x, y_0) }
    +
    \gamma_1 dy \lr{ -G(x_1, y) + G(x_1, y) }
    .
    \end{aligned}
    \end{equation}
    Referring to fig. 6. where the elements of the integrand are illustrated, we see that the normal \( I^{-1} d\Bx \) for the boundary of this region can be characterized as inwards.

    fig. 6. Inwards oriented normal for a Dirac spacelike basis.

References

[1] S.L. Salas and E. Hille. Calculus: one and several variables. Wiley New York, 1990.

New version of classical mechanics notes

January 1, 2021 Uncategorized , , , , , , , , ,

I’ve posted a new version of my classical mechanics notes compilation.  This version is not yet live on amazon, but you shouldn’t buy a copy of this “book” anyways, as it is horribly rough (if you want a copy, grab the free PDF instead.)  [I am going to buy a copy so that I can continue to edit a paper copy of it, but nobody else should.]

This version includes additional background material on Space Time Algebra (STA), i.e. the geometric algebra name for the Dirac/Clifford-algebra in 3+1 dimensions.  In particular, I’ve added material on reciprocal frames, the gradient and vector derivatives, line and surface integrals and the fundamental theorem for both.  Some of the integration theory content might make sense to move to a different book, but I’ll keep it with the rest of these STA notes for now.

Relativistic multivector surface integrals

December 31, 2020 math and physics play , , , , , , ,

[Click here for a PDF of this post]

Background.

This post is a continuation of:

Surface integrals.

[If mathjax doesn’t display properly for you, click here for a PDF of this post]

We’ve now covered line integrals and the fundamental theorem for line integrals, so it’s now time to move on to surface integrals.

Definition 1.1: Surface integral.

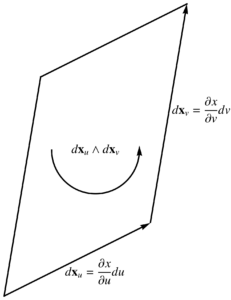
Given a two variable parameterization \( x = x(u,v) \), we write \( d^2\Bx = \Bx_u \wedge \Bx_v du dv \), and call
\begin{equation*}
\int F d^2\Bx\, G,
\end{equation*}
a surface integral, where \( F,G \) are arbitrary multivector functions.

Like our multivector line integral, this is intrinsically multivector valued, with a product of \( F \) with arbitrary grades, a bivector \( d^2 \Bx \), and \( G \), also potentially with arbitrary grades. Let’s consider an example.

Problem: Surface area integral example.

Given the hyperbolic surface parameterization \( x(\rho,\alpha) = \rho \gamma_0 e^{-\vcap \alpha} \), where \( \vcap = \gamma_{20} \) evaluate the indefinite integral
\begin{equation}\label{eqn:relativisticSurface:40}
\int \gamma_1 e^{\gamma_{21}\alpha} d^2 \Bx\, \gamma_2.
\end{equation}

Answer

We have \( \Bx_\rho = \gamma_0 e^{-\vcap \alpha} \) and \( \Bx_\alpha = \rho\gamma_{2} e^{-\vcap \alpha} \), so
\begin{equation}\label{eqn:relativisticSurface:60}
\begin{aligned}
d^2 \Bx
&=
(\Bx_\rho \wedge \Bx_\alpha) d\rho d\alpha \\
&=
\gpgradetwo{
\gamma_{0} e^{-\vcap \alpha} \rho\gamma_{2} e^{-\vcap \alpha}
}
d\rho d\alpha \\
&=
\rho \gamma_{02} d\rho d\alpha,
\end{aligned}
\end{equation}
so the integral is
\begin{equation}\label{eqn:relativisticSurface:80}
\begin{aligned}
\int \rho \gamma_1 e^{\gamma_{21}\alpha} \gamma_{022} d\rho d\alpha
&=
-\inv{2} \rho^2 \int \gamma_1 e^{\gamma_{21}\alpha} \gamma_{0} d\alpha \\
&=
\frac{\gamma_{01}}{2} \rho^2 \int e^{\gamma_{21}\alpha} d\alpha \\
&=
\frac{\gamma_{01}}{2} \rho^2 \gamma^{12} e^{\gamma_{21}\alpha} \\
&=
\frac{\rho^2 \gamma_{20}}{2} e^{\gamma_{21}\alpha}.
\end{aligned}
\end{equation}
Because \( F \) and \( G \) were both vectors, the resulting integral could only have been a multivector with grades 0,2,4. As it happens, there were no scalar nor pseudoscalar grades in the end result, and we ended up with the spacetime plane between \( \gamma_0 \), and \( \gamma_2 e^{\gamma_{21}\alpha} \), which are rotations of \(\gamma_2\) in the x,y plane. This is illustrated in fig. 1 (omitting scale and sign factors.)

fig. 1. Spacetime plane.

Fundamental theorem for surfaces.

For line integrals we saw that \( d\Bx \cdot \grad = \gpgradezero{ d\Bx \partial } \), and obtained the fundamental theorem for multivector line integrals by omitting the grade selection and using the multivector operator \( d\Bx \partial \) in the integrand directly. We have the same situation for surface integrals. In particular, we know that the \(\mathbb{R}^3\) Stokes theorem can be expressed in terms of \( d^2 \Bx \cdot \spacegrad \)

Problem: GA form of 3D Stokes’ theorem integrand.

Given an \(\mathbb{R}^3\) vector field \( \Bf \), show that
\begin{equation}\label{eqn:relativisticSurface:180}
\int dA \ncap \cdot \lr{ \spacegrad \cross \Bf }
=
-\int \lr{d^2\Bx \cdot \spacegrad } \cdot \Bf.
\end{equation}

Answer

Let \( d^2 \Bx = I \ncap dA \), implicitly fixing the relative orientation of the bivector area element compared to the chosen surface normal direction.
\begin{equation}\label{eqn:relativisticSurface:200}
\begin{aligned}
\int \lr{d^2\Bx \cdot \spacegrad } \cdot \Bf
&=
\int dA \gpgradeone{I \ncap \spacegrad } \cdot \Bf \\
&=
\int dA \lr{ I \lr{ \ncap \wedge \spacegrad} } \cdot \Bf \\
&=
\int dA \gpgradezero{ I^2 \lr{ \ncap \cross \spacegrad} \Bf } \\
&=
-\int dA \lr{ \ncap \cross \spacegrad} \cdot \Bf \\
&=
-\int dA \ncap \cdot \lr{ \spacegrad \cross \Bf }.
\end{aligned}
\end{equation}

The moral of the story is that the conventional dual form of the \(\mathbb{R}^3\) Stokes’ theorem can be written directly by projecting the gradient onto the surface area element. Geometrically, this projection operation has a rotational effect as well, since for bivector \( B \), and vector \( x \), the bivector-vector dot product \( B \cdot x \) is the component of \( x \) that lies in the plane \( B \wedge x = 0 \), but also rotated 90 degrees.

For multivector integration, we do not want an integral operator that includes such dot products. In the line integral case, we were able to achieve the same projective operation by using vector derivative instead of a dot product, and can do the same for the surface integral case. In particular

Theorem 1.1: Projection of gradient onto the tangent space.

Given a curvilinear representation of the gradient with respect to parameters \( u^0, u^1, u^2, u^3 \)
\begin{equation*}
\grad = \sum_\mu \Bx^\mu \PD{u^\mu}{},
\end{equation*}
the surface projection onto the tangent space associated with any two of those parameters, satisfies
\begin{equation*}
d^2 \Bx \cdot \grad = \gpgradeone{ d^2 \Bx \partial }.
\end{equation*}

Start proof:

Without loss of generality, we may pick \( u^0, u^1 \) as the parameters associated with the tangent space. The area element for the surface is
\begin{equation}\label{eqn:relativisticSurface:100}
d^2 \Bx = \Bx_0 \wedge \Bx_1 \,
du^0 du^1.
\end{equation}
Dotting this with the gradient gives
\begin{equation}\label{eqn:relativisticSurface:120}
\begin{aligned}
d^2 \Bx \cdot \grad
&=
du^0 du^1
\lr{ \Bx_0 \wedge \Bx_1 } \cdot \Bx^\mu \PD{u^\mu}{} \\
&=
du^0 du^1
\lr{
\Bx_0
\lr{\Bx_1 \cdot \Bx^\mu }
–
\Bx_1
\lr{\Bx_0 \cdot \Bx^\mu }
}
\PD{u^\mu}{} \\
&=
du^0 du^1
\lr{
\Bx_0 \PD{u^1}{}
–
\Bx_0 \PD{u^1}{}
}.
\end{aligned}
\end{equation}
On the other hand, the vector derivative for this surface is
\begin{equation}\label{eqn:relativisticSurface:140}
\partial
=
\Bx^0 \PD{u^0}{}
+
\Bx^1 \PD{u^1}{},
\end{equation}
so
\begin{equation}\label{eqn:relativisticSurface:160}
\begin{aligned}
\gpgradeone{d^2 \Bx \partial}
&=
du^0 du^1\,
\lr{ \Bx_0 \wedge \Bx_1 } \cdot
\lr{
\Bx^0 \PD{u^0}{}
+
\Bx^1 \PD{u^1}{}
} \\
&=
du^0 du^1
\lr{
\Bx_0 \PD{u^1}{}
–
\Bx_1 \PD{u^0}{}
}.
\end{aligned}
\end{equation}

End proof.

We now want to formulate the geometric algebra form of the fundamental theorem for surface integrals.

Theorem 1.2: Fundamental theorem for surface integrals.

Given multivector functions \( F, G \), and surface area element \( d^2 \Bx = \lr{ \Bx_u \wedge \Bx_v }\, du dv \), associated with a two parameter curve \( x(u,v) \), then
\begin{equation*}
\int_S F d^2\Bx \lrpartial G = \int_{\partial S} F d^1\Bx G,
\end{equation*}
where \( S \) is the integration surface, and \( \partial S \) designates its boundary, and the line integral on the RHS is really short hand for
\begin{equation*}
\int
\evalbar{ \lr{ F (-d\Bx_v) G } }{\Delta u}
+
\int
\evalbar{ \lr{ F (d\Bx_u) G } }{\Delta v},
\end{equation*}
which is a line integral that traverses the boundary of the surface with the opposite orientation to the circulation of the area element.

Start proof:

The vector derivative for this surface is
\begin{equation}\label{eqn:relativisticSurface:220}
\partial =
\Bx^u \PD{u}{}
+
\Bx^v \PD{v}{},
\end{equation}
so
\begin{equation}\label{eqn:relativisticSurface:240}
F d^2\Bx \lrpartial G
=
\PD{u}{} \lr{ F d^2\Bx\, \Bx^u G }
+
\PD{v}{} \lr{ F d^2\Bx\, \Bx^v G },
\end{equation}
where \( d^2\Bx\, \Bx^u \) is held constant with respect to \( u \), and \( d^2\Bx\, \Bx^v \) is held constant with respect to \( v \) (since the partials of the vector derivative act on \( F, G \), but not on the area element, nor on the reciprocal vectors of \( \lrpartial \) itself.) Note that
\begin{equation}\label{eqn:relativisticSurface:260}
d^2\Bx \wedge \Bx^u
=
du dv\, \lr{ \Bx_u \wedge \Bx_v } \wedge \Bx^u = 0,
\end{equation}
since \( \Bx^u \in sectionpan \setlr{ \Bx_u\, \Bx_v } \), so
\begin{equation}\label{eqn:relativisticSurface:280}
\begin{aligned}
d^2\Bx\, \Bx^u
&=
d^2\Bx \cdot \Bx^u
+
d^2\Bx \wedge \Bx^u \\
&=
d^2\Bx \cdot \Bx^u \\
&=
du dv\, \lr{ \Bx_u \wedge \Bx_v } \cdot \Bx^u \\
&=
-du dv\, \Bx_v.
\end{aligned}
\end{equation}
Similarly
\begin{equation}\label{eqn:relativisticSurface:300}
\begin{aligned}
d^2\Bx\, \Bx^v
&=
d^2\Bx \cdot \Bx^v \\
&=
du dv\, \lr{ \Bx_u \wedge \Bx_v } \cdot \Bx^v \\
&=
du dv\, \Bx_u.
\end{aligned}
\end{equation}
This leaves us with
\begin{equation}\label{eqn:relativisticSurface:320}
F d^2\Bx \lrpartial G
=
-du dv\,
\PD{u}{} \lr{ F \Bx_v G }
+
du dv\,
\PD{v}{} \lr{ F \Bx_u G },
\end{equation}
where \( \Bx_v, \Bx_u \) are held constant with respect to \( u,v \) respectively. Fortuitously, this constant condition can be dropped, since the antisymmetry of the wedge in the area element results in perfect cancellation. If these line elements are not held constant then
\begin{equation}\label{eqn:relativisticSurface:340}
\PD{u}{} \lr{ F \Bx_v G }
–
\PD{v}{} \lr{ F \Bx_u G }
=
F \lr{
\PD{v}{\Bx_u}
–
\PD{u}{\Bx_v}
} G
+
\lr{
\PD{u}{F} \Bx_v G
+
F \Bx_v \PD{u}{G}
}
+
\lr{
\PD{v}{F} \Bx_u G
+
F \Bx_u \PD{v}{G}
}
,
\end{equation}
but the mixed partial contribution is zero
\begin{equation}\label{eqn:relativisticSurface:360}
\begin{aligned}
\PD{v}{\Bx_u}
–
\PD{u}{\Bx_v}
&=
\PD{v}{} \PD{u}{x}
–
\PD{u}{} \PD{v}{x} \\
&=
0,
\end{aligned}
\end{equation}
by equality of mixed partials. We have two perfect differentials, and can evaluate each of these integrals
\begin{equation}\label{eqn:relativisticSurface:380}
\begin{aligned}
\int F d^2\Bx \lrpartial G
&=
-\int
du dv\,
\PD{u}{} \lr{ F \Bx_v G }
+
\int
du dv\,
\PD{v}{} \lr{ F \Bx_u G } \\
&=
-\int
dv\,
\evalbar{ \lr{ F \Bx_v G } }{\Delta u}
+
\int
du\,
\evalbar{ \lr{ F \Bx_u G } }{\Delta v} \\
&=
\int
\evalbar{ \lr{ F (-d\Bx_v) G } }{\Delta u}
+
\int
\evalbar{ \lr{ F (d\Bx_u) G } }{\Delta v}.
\end{aligned}
\end{equation}
We use the shorthand \( d^1 \Bx = d\Bx_u – d\Bx_v \) to write
\begin{equation}\label{eqn:relativisticSurface:400}
\int_S F d^2\Bx \lrpartial G = \int_{\partial S} F d^1\Bx G,
\end{equation}
with the understanding that this is really instructions to evaluate the line integrals in the last step of \ref{eqn:relativisticSurface:380}.

End proof.

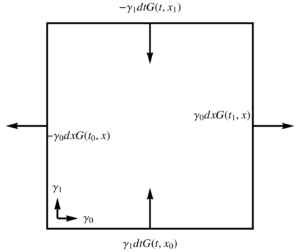
Problem: Integration in the t,y plane.

Let \( x(t,y) = c t \gamma_0 + y \gamma_2 \). Write out both sides of the fundamental theorem explicitly.

Answer

Let’s designate the tangent basis vectors as
\begin{equation}\label{eqn:relativisticSurface:420}
\Bx_0 = \PD{t}{x} = c \gamma_0,
\end{equation}
and
\begin{equation}\label{eqn:relativisticSurface:440}
\Bx_2 = \PD{y}{x} = \gamma_2,
\end{equation}
so the vector derivative is
\begin{equation}\label{eqn:relativisticSurface:460}
\partial
= \inv{c} \gamma^0 \PD{t}{}
+ \gamma^2 \PD{y}{},
\end{equation}
and the area element is
\begin{equation}\label{eqn:relativisticSurface:480}
d^2 \Bx = c \gamma_0 \gamma_2.
\end{equation}
The fundamental theorem of surface integrals is just a statement that
\begin{equation}\label{eqn:relativisticSurface:500}
\int_{t_0}^{t_1} c dt
\int_{y_0}^{y_1} dy
F \gamma_0 \gamma_2 \lr{
\inv{c} \gamma^0 \PD{t}{}
+ \gamma^2 \PD{y}{}
} G
=
\int F \lr{ c \gamma_0 dt – \gamma_2 dy } G,
\end{equation}
where the RHS, when stated explicitly, really means
\begin{equation}\label{eqn:relativisticSurface:520}
\begin{aligned}
\int &F \lr{ c \gamma_0 dt – \gamma_2 dy } G
=
\int_{t_0}^{t_1} c dt \lr{ F(t,y_1) \gamma_0 G(t, y_1) – F(t,y_0) \gamma_0 G(t, y_0) } \\
&\qquad –
\int_{y_0}^{y_1} dy \lr{ F(t_1,y) \gamma_2 G(t_1, y) – F(t_0,y) \gamma_0 G(t_0, y) }.
\end{aligned}
\end{equation}
In this particular case, since \( \Bx_0 = c \gamma_0, \Bx_2 = \gamma_2 \) are both constant functions that depend on neither \( t \) nor \( y \), it is easy to derive the full expansion of \ref{eqn:relativisticSurface:520} directly from the LHS of \ref{eqn:relativisticSurface:500}.

Problem: A cylindrical hyperbolic surface.

Generalizing the example surface integral from \ref{eqn:relativisticSurface:40}, let
\begin{equation}\label{eqn:relativisticSurface:540}
x(\rho, \alpha) = \rho e^{-\vcap \alpha/2} x(0,1) e^{\vcap \alpha/2},
\end{equation}
where \( \rho \) is a scalar, and \( \vcap = \cos\theta_k\gamma_{k0} \) is a unit spatial bivector, and \( \cos\theta_k \) are direction cosines of that vector. This is a composite transformation, where the \( \alpha \) variation boosts the \( x(0,1) \) four-vector, and the \( \rho \) parameter contracts or increases the magnitude of this vector, resulting in \( x \) spanning a hyperbolic region of spacetime.

Compute the tangent and reciprocal basis, the area element for the surface, and explicitly state both sides of the fundamental theorem.

Answer

For the tangent basis vectors we have
\begin{equation}\label{eqn:relativisticSurface:560}
\Bx_\rho = \PD{\rho}{x} =
e^{-\vcap \alpha/2} x(0,1) e^{\vcap \alpha/2} = \frac{x}{\rho},
\end{equation}
and
\begin{equation}\label{eqn:relativisticSurface:580}
\Bx_\alpha = \PD{\alpha}{x} =
\lr{-\vcap/2} x
+
x \lr{ \vcap/2 }
=
x \cdot \vcap.
\end{equation}
These vectors \( \Bx_\rho, \Bx_\alpha \) are orthogonal, as \( x \cdot \vcap \) is the projection of \( x \) onto the spacetime plane \( x \wedge \vcap = 0 \), but rotated so that \( x \cdot \lr{ x \cdot \vcap } = 0 \). Because of this orthogonality, the vector derivative for this tangent space is
\begin{equation}\label{eqn:relativisticSurface:600}
\partial =
\inv{x \cdot \vcap} \PD{\alpha}{}
+
\frac{\rho}{x}
\PD{\rho}{}
.
\end{equation}
The area element is
\begin{equation}\label{eqn:relativisticSurface:620}
\begin{aligned}
d^2 \Bx
&=
d\rho d\alpha\,
\frac{x}{\rho} \wedge \lr{ x \cdot \vcap } \\
&=
\inv{\rho} d\rho d\alpha\,
x \lr{ x \cdot \vcap }
.
\end{aligned}
\end{equation}
The full statement of the fundamental theorem for this surface is
\begin{equation}\label{eqn:relativisticSurface:640}
\int_S
d\rho d\alpha\,
F
\lr{
\inv{\rho} x \lr{ x \cdot \vcap }
}
\lr{
\inv{x \cdot \vcap} \PD{\alpha}{}
+
\frac{\rho}{x}
\PD{\rho}{}
}
G
=
\int_{\partial S}
F \lr{ d\rho \frac{x}{\rho} – d\alpha \lr{ x \cdot \vcap } } G.
\end{equation}
As in the previous example, due to the orthogonality of the tangent basis vectors, it’s easy to show find the RHS directly from the LHS.

Problem: Simple example with non-orthogonal tangent space basis vectors.

Let \( x(u,v) = u a + v b \), where \( u,v \) are scalar parameters, and \( a, b \) are non-null and non-colinear constant four-vectors. Write out the fundamental theorem for surfaces with respect to this parameterization.

Answer

The tangent basis vectors are just \( \Bx_u = a, \Bx_v = b \), with reciprocals
\begin{equation}\label{eqn:relativisticSurface:660}
\Bx^u = \Bx_v \cdot \inv{ \Bx_u \wedge \Bx_v } = b \cdot \inv{ a \wedge b },
\end{equation}
and
\begin{equation}\label{eqn:relativisticSurface:680}
\Bx^v = -\Bx_u \cdot \inv{ \Bx_u \wedge \Bx_v } = -a \cdot \inv{ a \wedge b }.
\end{equation}
The fundamental theorem, with respect to this surface, when written out explicitly takes the form
\begin{equation}\label{eqn:relativisticSurface:700}
\int F \, du dv\, \lr{ a \wedge b } \inv{ a \wedge b } \cdot \lr{ a \PD{u}{} – b \PD{v}{} } G
=
\int F \lr{ a du – b dv } G.
\end{equation}
This is a good example to illustrate the geometry of the line integral circulation.
Suppose that we are integrating over \( u \in [0,1], v \in [0,1] \). In this case, the line integral really means
\begin{equation}\label{eqn:relativisticSurface:720}
\begin{aligned}
\int &F \lr{ a du – b dv } G
=
+
\int F(u,1) (+a du) G(u,1)
+
\int F(u,0) (-a du) G(u,0) \\
&\quad+
\int F(1,v) (-b dv) G(1,v)
+
\int F(0,v) (+b dv) G(0,v),
\end{aligned}
\end{equation}
which is a path around the spacetime parallelogram spanned by \( u, v \), as illustrated in fig. 1, which illustrates the orientation of the bivector area element with the arrows around the exterior of the parallelogram: \( 0 \rightarrow a \rightarrow a + b \rightarrow b \rightarrow 0 \).

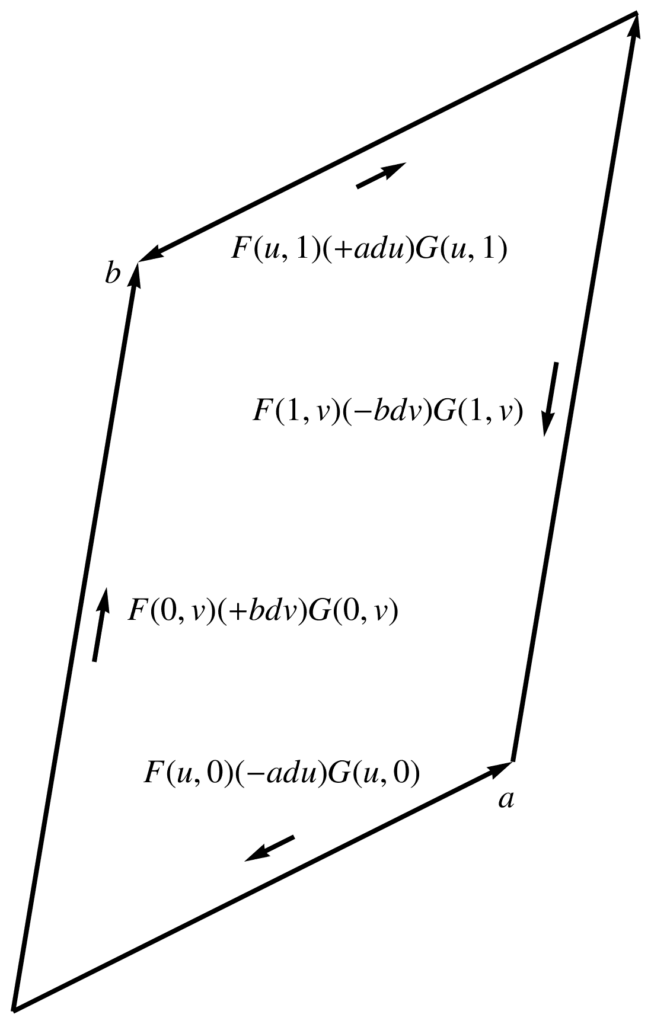
fig. 2. Line integral orientation.

A couple more reciprocal frame examples.

December 14, 2020 math and physics play , , , , , , , , , , , , ,

[If mathjax doesn’t display properly for you, click here for a PDF of this post]

This post logically follows both of the following:

  1. Curvilinear coordinates and gradient in spacetime, and reciprocal frames, and
  2. Lorentz transformations in Space Time Algebra (STA)

The PDF linked above above contains all the content from this post plus (1.) above [to be edited later into a more logical sequence.]

More examples.

Here are a few additional examples of reciprocal frame calculations.

Problem: Unidirectional arbitrary functional dependence.

Let
\begin{equation}\label{eqn:reciprocal:2540}
x = a f(u),
\end{equation}
where \( a \) is a constant vector and \( f(u)\) is some arbitrary differentiable function with a non-zero derivative in the region of interest.

Answer

Here we have just a single tangent space direction (a line in spacetime) with tangent vector
\begin{equation}\label{eqn:reciprocal:2400}
\Bx_u = a \PD{u}{f} = a f_u,
\end{equation}
so we see that the tangent space vectors are just rescaled values of the direction vector \( a \).
This is a simple enough parameterization that we can compute the reciprocal frame vector explicitly using the gradient. We expect that \( \Bx^u = 1/\Bx_u \), and find
\begin{equation}\label{eqn:reciprocal:2420}
\inv{a} \cdot x = f(u),
\end{equation}
but for constant \( a \), we know that \( \grad a \cdot x = a \), so taking gradients of both sides we find
\begin{equation}\label{eqn:reciprocal:2440}
\inv{a} = \grad f = \PD{u}{f} \grad u,
\end{equation}
so the reciprocal vector is
\begin{equation}\label{eqn:reciprocal:2460}
\Bx^u = \grad u = \inv{a f_u},
\end{equation}
as expected.

Problem: Linear two variable parameterization.

Let \( x = a u + b v \), where \( x \wedge a \wedge b = 0 \) represents spacetime plane (also the tangent space.) Find the curvilinear coordinates and their reciprocals.

Answer

The frame vectors are easy to compute, as they are just
\begin{equation}\label{eqn:reciprocal:1960}
\begin{aligned}
\Bx_u &= \PD{u}{x} = a \\
\Bx_v &= \PD{v}{x} = b.
\end{aligned}
\end{equation}
This is an example of a parametric equation that we can easily invert, as we have
\begin{equation}\label{eqn:reciprocal:1980}
\begin{aligned}
x \wedge a &= – v \lr{ a \wedge b } \\
x \wedge b &= u \lr{ a \wedge b },
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:reciprocal:2000}
\begin{aligned}
u
&= \inv{ a \wedge b } \cdot \lr{ x \wedge b } \\
&= \inv{ \lr{a \wedge b}^2 } \lr{ a \wedge b } \cdot \lr{ x \wedge b } \\
&=
\frac{
\lr{b \cdot x} \lr{ a \cdot b }
–
\lr{a \cdot x} \lr{ b \cdot b }
}{ \lr{a \wedge b}^2 }
\end{aligned}
\end{equation}
\begin{equation}\label{eqn:reciprocal:2020}
\begin{aligned}
v &= -\inv{ a \wedge b } \cdot \lr{ x \wedge a } \\
&= -\inv{ \lr{a \wedge b}^2 } \lr{ a \wedge b } \cdot \lr{ x \wedge a } \\
&=
-\frac{
\lr{b \cdot x} \lr{ a \cdot a }
–
\lr{a \cdot x} \lr{ a \cdot b }
}{ \lr{a \wedge b}^2 }
\end{aligned}
\end{equation}
Recall that \( \grad \lr{ a \cdot x} = a \), if \( a \) is a constant, so our gradients are just
\begin{equation}\label{eqn:reciprocal:2040}
\begin{aligned}
\grad u
&=
\frac{
b \lr{ a \cdot b }
–
a
\lr{ b \cdot b }
}{ \lr{a \wedge b}^2 } \\
&=
b \cdot \inv{ a \wedge b },
\end{aligned}
\end{equation}
and
\begin{equation}\label{eqn:reciprocal:2060}
\begin{aligned}
\grad v
&=
-\frac{
b \lr{ a \cdot a }
–
a \lr{ a \cdot b }
}{ \lr{a \wedge b}^2 } \\
&=
-a \cdot \inv{ a \wedge b }.
\end{aligned}
\end{equation}
Expressed in terms of the frame vectors, this is just
\begin{equation}\label{eqn:reciprocal:2080}
\begin{aligned}
\Bx^u &= \Bx_v \cdot \inv{ \Bx_u \wedge \Bx_v } \\
\Bx^v &= -\Bx_u \cdot \inv{ \Bx_u \wedge \Bx_v },
\end{aligned}
\end{equation}
so we were able to show, for this special two parameter linear case, that the explicit evaluation of the gradients has the exact structure that we intuited that the reciprocals must have, provided they are constrained to the spacetime plane \( a \wedge b \). It is interesting to observe how this structure falls out of the linear system solution so directly. Also note that these reciprocals are not defined at the origin of the \( (u,v) \) parameter space.

Problem: Quadratic two variable parameterization.

Now consider a variation of the previous problem, with \( x = a u^2 + b v^2 \). Find the curvilinear coordinates and their reciprocals.

Answer

\begin{equation}\label{eqn:reciprocal:2100}
\begin{aligned}
\Bx_u &= \PD{u}{x} = 2 u a \\
\Bx_v &= \PD{v}{x} = 2 v b.
\end{aligned}
\end{equation}
Our tangent space is still the \( a \wedge b \) plane (as is the surface itself), but the spacing of the cells starts getting wider in proportion to \( u, v \).
Utilizing the work from the previous problem, we have
\begin{equation}\label{eqn:reciprocal:2120}
\begin{aligned}
2 u \grad u &=
b \cdot \inv{ a \wedge b } \\
2 v \grad v &=
-a \cdot \inv{ a \wedge b }.
\end{aligned}
\end{equation}
A bit of rearrangement can show that this is equivalent to the reciprocal frame identities. This is a second demonstration that the gradient and the algebraic formulations for the reciprocals match, at least for these special cases of linear non-coupled parameterizations.

Problem: Reciprocal frame for generalized cylindrical parameterization.

Let the vector parameterization be \( x(\rho,\theta) = \rho e^{-i\theta/2} x(\rho_0, \theta_0) e^{i \theta} \), where \( i^2 = \pm 1 \) is a unit bivector (\(+1\) for a boost, and \(-1\) for a rotation), and where \(\theta, \rho\) are scalars. Find the tangent space vectors and their reciprocals.

fig. 1. “Cylindrical” boost parameterization.

Note that this is cylindrical parameterization for the rotation case, and traces out hyperbolic regions for the boost case. The boost case is illustrated in fig. 1 where hyperbolas in the light cone are found for boosts of \( \gamma_0\) with various values of \(\rho\), and the spacelike hyperbolas are boosts of \( \gamma_1 \), again for various values of \( \rho \).

Answer

The tangent space vectors are
\begin{equation}\label{eqn:reciprocal:2480}
\Bx_\rho = \frac{x}{\rho},
\end{equation}
and

\begin{equation}\label{eqn:reciprocal:2500}
\begin{aligned}
\Bx_\theta
&= -\frac{i}{2} x + x \frac{i}{2} \\
&= x \cdot i.
\end{aligned}
\end{equation}
Recall that \( x \cdot i \) lies perpendicular to \( x \) (in the plane \( i \)), as illustrated in fig. 2. This means that \( \Bx_\rho \) and \( \Bx_\theta \) are orthogonal, so we can find the reciprocal vectors by just inverting them
\begin{equation}\label{eqn:reciprocal:2520}
\begin{aligned}
\Bx^\rho &= \frac{\rho}{x} \\
\Bx^\theta &= \frac{1}{x \cdot i}.
\end{aligned}
\end{equation}

fig. 2. Projection and rejection geometry.

Parameterization of a general linear transformation.

Given \( N \) parameters \( u^0, u^1, \cdots u^{N-1} \), a general linear transformation from the parameter space to the vector space has the form
\begin{equation}\label{eqn:reciprocal:2160}
x =
{a^\alpha}_\beta \gamma_\alpha u^\beta,
\end{equation}
where \( \beta \in [0, \cdots, N-1] \) and \( \alpha \in [0,3] \).
For such a general transformation, observe that the curvilinear basis vectors are
\begin{equation}\label{eqn:reciprocal:2180}
\begin{aligned}
\Bx_\mu
&= \PD{u^\mu}{x} \\
&= \PD{u^\mu}{}
{a^\alpha}_\beta \gamma_\alpha u^\beta \\
&=
{a^\alpha}_\mu \gamma_\alpha.
\end{aligned}
\end{equation}
We find an interpretation of \( {a^\alpha}_\mu \) by dotting \( \Bx_\mu \) with the reciprocal frame vectors of the standard basis
\begin{equation}\label{eqn:reciprocal:2200}
\begin{aligned}
\Bx_\mu \cdot \gamma^\nu
&=
{a^\alpha}_\mu \lr{ \gamma_\alpha \cdot \gamma^\nu } \\
&=
{a^\nu}_\mu,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:reciprocal:2220}
x = \Bx_\mu u^\mu.
\end{equation}
We are able to reinterpret \ref{eqn:reciprocal:2160} as a contraction of the tangent space vectors with the parameters, scaling and summing these direction vectors to characterize all the points in the tangent plane.

Theorem 1.1: Projecting onto the tangent space.

Let \( T \) represent the tangent space. The projection of a vector onto the tangent space has the form
\begin{equation}\label{eqn:reciprocal:2560}
\textrm{Proj}_{\textrm{T}} y = \lr{ y \cdot \Bx^\mu } \Bx_\mu = \lr{ y \cdot \Bx_\mu } \Bx^\mu.
\end{equation}

Start proof:

Let’s designate \( a \) as the portion of the vector \( y \) that lies outside of the tangent space
\begin{equation}\label{eqn:reciprocal:2260}
y = y^\mu \Bx_\mu + a.
\end{equation}
If we knew the coordinates \( y^\mu \), we would have a recipe for the projection.
Algebraically, requiring that \( a \) lies outside of the tangent space, is equivalent to stating \( a \cdot \Bx_\mu = a \cdot \Bx^\mu = 0 \). We use that fact, and then take dot products
\begin{equation}\label{eqn:reciprocal:2280}
\begin{aligned}
y \cdot \Bx^\nu
&= \lr{ y^\mu \Bx_\mu + a } \cdot \Bx^\nu \\
&= y^\nu,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:reciprocal:2300}
y = \lr{ y \cdot \Bx^\mu } \Bx_\mu + a.
\end{equation}
Similarly, the tangent space projection can be expressed as a linear combination of reciprocal basis elements
\begin{equation}\label{eqn:reciprocal:2320}
y = y_\mu \Bx^\mu + a.
\end{equation}
Dotting with \( \Bx_\mu \), we have
\begin{equation}\label{eqn:reciprocal:2340}
\begin{aligned}
y \cdot \Bx^\mu
&= \lr{ y_\alpha \Bx^\alpha + a } \cdot \Bx_\mu \\
&= y_\mu,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:reciprocal:2360}
y = \lr{ y \cdot \Bx^\mu } \Bx_\mu + a.
\end{equation}
We find the two stated ways of computing the projection.

Observe that, for the special case that all of \( \setlr{ \Bx_\mu } \) are orthogonal, the equivalence of these two projection methods follows directly, since
\begin{equation}\label{eqn:reciprocal:2380}
\begin{aligned}
\lr{ y \cdot \Bx^\mu } \Bx_\mu
&=
\lr{ y \cdot \inv{\Bx_\mu} } \inv{\Bx^\mu} \\
&=
\lr{ y \cdot \frac{\Bx_\mu}{\lr{\Bx_\mu}^2 } } \frac{\Bx^\mu}{\lr{\Bx^\mu}^2} \\
&=
\lr{ y \cdot \Bx_\mu } \Bx^\mu.
\end{aligned}
\end{equation}

End proof.