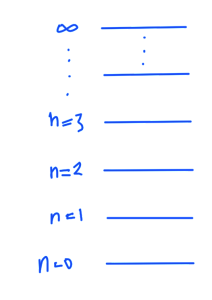Heisenberg-picture operator

PHY1520H Graduate Quantum Mechanics. Lecture 5: time evolution of coherent states, and charged particles in a magnetic field. Taught by Prof. Arun Paramekanti

October 1, 2015 phy1520 , , , , , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course PHY1520, Graduate Quantum Mechanics, taught by Prof. Paramekanti, covering \textchapref{{1}} [1] content.

Coherent states (cont.)

A coherent state for the SHO \( H = \lr{ N + \inv{2} } \Hbar \omega \) was given by

\begin{equation}\label{eqn:qmLecture5:20}
a \ket{z} = z \ket{z},
\end{equation}

where we showed that

\begin{equation}\label{eqn:qmLecture5:40}
\ket{z} = c_0 e^{ z a^\dagger } \ket{0}.
\end{equation}

In the Heisenberg picture we found

\begin{equation}\label{eqn:qmLecture5:60}
\begin{aligned}
a_{\textrm{H}}(t) &= e^{i H t/\Hbar} a e^{-i H t/\Hbar} = a e^{-i\omega t} \\
a_{\textrm{H}}^\dagger(t) &= e^{i H t/\Hbar} a^\dagger e^{-i H t/\Hbar} = a^\dagger e^{i\omega t}.
\end{aligned}
\end{equation}

Recall that the position and momentum representation of the ladder operators was

\begin{equation}\label{eqn:qmLecture5:80}
\begin{aligned}
a &= \inv{\sqrt{2}} \lr{ \hat{x} \sqrt{\frac{m \omega}{\Hbar}} + i \hat{p} \sqrt{\inv{m \Hbar \omega}} } \\
a^\dagger &= \inv{\sqrt{2}} \lr{ \hat{x} \sqrt{\frac{m \omega}{\Hbar}} – i \hat{p} \sqrt{\inv{m \Hbar \omega}} },
\end{aligned}
\end{equation}

or equivalently
\begin{equation}\label{eqn:qmLecture5:100}
\begin{aligned}
\hat{x} &= \lr{ a + a^\dagger } \sqrt{\frac{\Hbar}{ 2 m \omega}} \\
\hat{p} &= i \lr{ a^\dagger – a } \sqrt{\frac{m \Hbar \omega}{2}}.
\end{aligned}
\end{equation}

Given this we can compute expectation value of position operator

\begin{equation}\label{eqn:qmLecture5:120}
\begin{aligned}
\bra{z} \hat{x} \ket{z}
&=
\sqrt{\frac{\Hbar}{ 2 m \omega}}
\bra{z}
\lr{ a + a^\dagger }
\ket{z} \\
&=
\lr{ z + z^\conj } \sqrt{\frac{\Hbar}{ 2 m \omega}} \\
&=
2 \textrm{Re} z \sqrt{\frac{\Hbar}{ 2 m \omega}} .
\end{aligned}
\end{equation}

Similarly

\begin{equation}\label{eqn:qmLecture5:140}
\begin{aligned}
\bra{z} \hat{p} \ket{z}
&=
i \sqrt{\frac{m \Hbar \omega}{2}}
\bra{z}
\lr{ a^\dagger – a }
\ket{z} \\
&=
\sqrt{\frac{m \Hbar \omega}{2}}
2 \textrm{Im} z.
\end{aligned}
\end{equation}

How about the expectation of the Heisenberg position operator? That is

\begin{equation}\label{eqn:qmLecture5:160}
\begin{aligned}
\bra{z} \hat{x}_{\textrm{H}}(t) \ket{z}
&=
\sqrt{\frac{\Hbar}{2 m \omega}} \bra{z} \lr{ a + a^\dagger } \ket{z} \\
&=
\sqrt{\frac{\Hbar}{2 m \omega}} \lr{ z e^{-i \omega t} + z^\conj e^{i \omega t}} \\
&=
\sqrt{\frac{\Hbar}{2 m \omega}} \lr{ \lr{z + z^\conj} \cos( \omega t ) -i \lr{ z – z^\conj } \sin( \omega t) } \\
&=
\sqrt{\frac{\Hbar}{2 m \omega}} \lr{ \expectation{x(0)} \sqrt{ \frac{2 m \omega}{\Hbar}} \cos( \omega t ) -i \expectation{p(0)} i \sqrt{\frac{2 m \omega}{\Hbar} } \sin( \omega t) } \\
&=
\expectation{x(0)} \cos( \omega t ) + \frac{\expectation{p(0)}}{m \omega} \sin( \omega t) .
\end{aligned}
\end{equation}

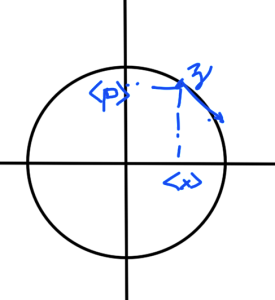
We find that the average of the Heisenberg position operator evolves in time in exactly the same fashion as position in the classical Harmonic oscillator. This phase space like trajectory is sketched in fig. 1.

fig. 1. phase space like trajectory

fig. 1. phase space like trajectory

In the text it is shown that we have the same structure for the Heisenberg operator itself, before taking expectations

\begin{equation}\label{eqn:qmLecture5:220}
\hat{x}_{\textrm{H}}(t)
=
{x(0)} \cos( \omega t ) + \frac{{p(0)}}{m \omega} \sin( \omega t).
\end{equation}

Where the coherent states become useful is that we will see that the second moments of position and momentum are not time dependent with respect to the coherent states. Such states remain localized.

Uncertainty

First note that using the commutator relationship we have

\begin{equation}\label{eqn:qmLecture5:180}
\begin{aligned}
\bra{z} a a^\dagger \ket{z}
&=
\bra{z} \lr{ \antisymmetric{a}{a^\dagger} + a^\dagger a } \ket{z} \\
&=
\bra{z} \lr{ 1 + a^\dagger a } \ket{z}.
\end{aligned}
\end{equation}

For the second moment we have

\begin{equation}\label{eqn:qmLecture5:200}
\begin{aligned}
\bra{z} \hat{x}^2 \ket{z}
&=
\frac{\Hbar}{ 2 m \omega}
\bra{z} \lr{a + a^\dagger } \lr{a + a^\dagger } \ket{z} \\
&=
\frac{\Hbar}{ 2 m \omega}
\bra{z} \lr{
a^2 + {(a^\dagger)}^2 + a a^\dagger + a^\dagger a
} \ket{z} \\
&=
\frac{\Hbar}{ 2 m \omega}
\bra{z} \lr{
a^2 + {(a^\dagger)}^2 + 2 a^\dagger a + 1
} \ket{z} \\
&=
\frac{\Hbar}{ 2 m \omega}
\lr{ z^2 + {(z^\conj)}^2 + 2 z^\conj z + 1} \ket{z} \\
&=
\frac{\Hbar}{ 2 m \omega}
\lr{ z + z^\conj }^2
+
\frac{\Hbar}{ 2 m \omega}.
\end{aligned}
\end{equation}

We find

\begin{equation}\label{eqn:qmLecture5:240}
\sigma_x^2 = \frac{\Hbar}{ 2 m \omega},
\end{equation}

and

\begin{equation}\label{eqn:qmLecture5:260}
\sigma_p^2 = \frac{m \Hbar \omega}{2}
\end{equation}

so

\begin{equation}\label{eqn:qmLecture5:280}
\sigma_x^2 \sigma_p^2 = \frac{\Hbar^2}{4},
\end{equation}

or

\begin{equation}\label{eqn:qmLecture5:300}
\sigma_x \sigma_p = \frac{\Hbar}{2}.
\end{equation}

This is the minimum uncertainty.

Quantum Field theory

In Quantum Field theory the ideas of isolated oscillators is used to model particle creation. The lowest energy state (a no particle, vacuum state) is given the lowest energy level, with each additional quantum level modeling a new particle creation state as sketched in fig. 2.

fig. 2. QFT energy levels

fig. 2. QFT energy levels

We have to imagine many oscillators, each with a distinct vacuum energy \( \sim \Bk^2 \) . The Harmonic oscillator can be used to model the creation of particles with \( \Hbar \omega \) energy differences from that “vacuum energy”.

Charged particle in a magnetic field

In the classical case ( with SI units or \( c = 1 \) ) we have

\begin{equation}\label{eqn:qmLecture5:320}
\BF = q \BE + q \Bv \cross \BB.
\end{equation}

Alternately, we can look at the Hamiltonian view of the system, written in terms of potentials

\begin{equation}\label{eqn:qmLecture5:340}
\BB = \spacegrad \cross \BA,
\end{equation}
\begin{equation}\label{eqn:qmLecture5:360}
\BE = – \spacegrad \phi – \PD{t}{\BA}.
\end{equation}

Note that the curl form for the magnetic field implies one of the required Maxwell’s equations \( \spacegrad \cdot \BB = 0 \).

Ignoring time dependence of the potentials, the Hamiltonian can be expressed as

\begin{equation}\label{eqn:qmLecture5:380}
H = \inv{2 m} \lr{ \Bp – q \BA }^2 + q \phi.
\end{equation}

In this Hamiltonian the vector \( \Bp \) is called the canonical momentum, the momentum conjugate to position in phase space.

It is left as an exercise to show that the Lorentz force equation results from application of the Hamiltonian equations of motion, and that the velocity is given by \( \Bv = (\Bp – q \BA)/m \).

For quantum mechanics, we use the same Hamiltonian, but promote our position, momentum and potentials to operators.

\begin{equation}\label{eqn:qmLecture5:400}
\hat{H} = \inv{2 m} \lr{ \hat{\Bp} – q \hat{\BA}(\Br, t) }^2 + q \hat{\phi}(\Br, t).
\end{equation}

Gauge invariance

Can we say anything about this before looking at the question of a particle in a magnetic field?

Recall that the we can make a gauge transformation of the form

\label{eqn:qmLecture5:420a}
\begin{equation}\label{eqn:qmLecture5:420}
\BA \rightarrow \BA + \spacegrad \chi
\end{equation}
\begin{equation}\label{eqn:qmLecture5:440}
\phi \rightarrow \phi – \PD{t}{\chi}
\end{equation}

Does this notion of gauge invariance also carry over to the Quantum Hamiltonian. After gauge transformation we have

\begin{equation}\label{eqn:qmLecture5:460}
\hat{H}’
= \inv{2 m} \lr{ \hat{\Bp} – q \BA – q \spacegrad \chi }^2 + q \lr{ \phi – \PD{t}{\chi} }
\end{equation}

Now we are in a mess, since this function \( \chi \) can make the Hamiltonian horribly complicated. We don’t see how gauge invariance can easily be applied to the quantum problem. Next time we will introduce a transformation that resolves some of this mess.

Question: Lorentz force from classical electrodynamic Hamiltonian

Given the classical Hamiltonian

\begin{equation}\label{eqn:qmLecture5:381}
H = \inv{2 m} \lr{ \Bp – q \BA }^2 + q \phi.
\end{equation}

apply the Hamiltonian equations of motion

\begin{equation}\label{eqn:qmLecture5:480}
\begin{aligned}
\ddt{\Bp} &= – \PD{\Bq}{H} \\
\ddt{\Bq} &= \PD{\Bp}{H},
\end{aligned}
\end{equation}

to show that this is the Hamiltonian that describes the Lorentz force equation, and to find the velocity in terms of the canonical momentum and vector potential.

Answer

The particle velocity follows easily

\begin{equation}\label{eqn:qmLecture5:500}
\begin{aligned}
\Bv
&= \ddt{\Br} \\
&= \PD{\Bp}{H} \\
&= \inv{m} \lr{ \Bp – a \BA }.
\end{aligned}
\end{equation}

For the Lorentz force we can proceed in the coordinate representation

\begin{equation}\label{eqn:qmLecture5:520}
\begin{aligned}
\ddt{p_k}
&= – \PD{x_k}{H} \\
&= – \frac{2}{2m} \lr{ p_m – q A_m } \PD{x_k}{}\lr{ p_m – q A_m } – q \PD{x_k}{\phi} \\
&= q v_m \PD{x_k}{A_m} – q \PD{x_k}{\phi},
\end{aligned}
\end{equation}

We also have

\begin{equation}\label{eqn:qmLecture5:540}
\begin{aligned}
\ddt{p_k}
&=
\ddt{} \lr{m x_k + q A_k } \\
&=
m \frac{d^2 x_k}{dt^2} + q \PD{x_m}{A_k} \frac{d x_m}{dt} + q \PD{t}{A_k}.
\end{aligned}
\end{equation}

Putting these together we’ve got

\begin{equation}\label{eqn:qmLecture5:560}
\begin{aligned}
m \frac{d^2 x_k}{dt^2}
&= q v_m \PD{x_k}{A_m} – q \PD{x_k}{\phi},
– q \PD{x_m}{A_k} \frac{d x_m}{dt} – q \PD{t}{A_k} \\
&=
q v_m \lr{ \PD{x_k}{A_m} – \PD{x_m}{A_k} } + q E_k \\
&=
q v_m \epsilon_{k m s} B_s + q E_k,
\end{aligned}
\end{equation}

or

\begin{equation}\label{eqn:qmLecture5:580}
\begin{aligned}
m \frac{d^2 \Bx}{dt^2}
&=
q \Be_k v_m \epsilon_{k m s} B_s + q E_k \\
&= q \Bv \cross \BB + q \BE.
\end{aligned}
\end{equation}

Question: Show gauge invariance of the magnetic and electric fields

After the gauge transformation of \ref{eqn:qmLecture5:420} show that the electric and magnetic fields are unaltered.

Answer

For the magnetic field the transformed field is

\begin{equation}\label{eqn:qmLecture5:600}
\begin{aligned}
\BB’
&= \spacegrad \cross \lr{ \BA + \spacegrad \chi } \\
&= \spacegrad \cross \BA + \spacegrad \cross \lr{ \spacegrad \chi } \\
&= \spacegrad \cross \BA \\
&= \BB.
\end{aligned}
\end{equation}

\begin{equation}\label{eqn:qmLecture5:620}
\begin{aligned}
\BE’
&=
– \PD{t}{\BA’} – \spacegrad \phi’ \\
&=
– \PD{t}{}\lr{\BA + \spacegrad \chi} – \spacegrad \lr{ \phi – \PD{t}{\chi}} \\
&=
– \PD{t}{\BA} – \spacegrad \phi \\
&=
\BE.
\end{aligned}
\end{equation}

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

Gauge transformation of free particle Hamiltonian

September 15, 2015 math and physics play , , , , , ,


[Click here for a PDF of this post with nicer formatting]

Question:

Given a gauge transformation of the free particle Hamiltonian to

\begin{equation}\label{eqn:gaugeTx:20}
H = \inv{2 m} \BPi \cdot \BPi + e \phi,
\end{equation}

where

\begin{equation}\label{eqn:gaugeTx:40}
\BPi = \Bp – \frac{e}{c} \BA,
\end{equation}

calculate \( m d\Bx/dt \), \( \antisymmetric{\Pi_i}{\Pi_j} \), and \( m d^2\Bx/dt^2 \), where \( \Bx \) is the Heisenberg picture position operator, and the fields are functions only of position \( \phi = \phi(\Bx), \BA = \BA(\Bx) \).

Answer

The final results for these calculations are found in [1], but seem worth deriving to exercise our commutator muscles.

Heisenberg picture velocity operator

The first order of business is the Heisenberg picture velocity operator, but first note

\begin{equation}\label{eqn:gaugeTx:60}
\begin{aligned}
\BPi \cdot \BPi
&= \lr{ \Bp – \frac{e}{c} \BA} \cdot \lr{ \Bp – \frac{e}{c} \BA} \\
&= \Bp^2 – \frac{e}{c} \lr{ \BA \cdot \Bp + \Bp \cdot \BA } + \frac{e^2}{c^2} \BA^2.
\end{aligned}
\end{equation}

The time evolution of the Heisenberg picture position operator is therefore

\begin{equation}\label{eqn:gaugeTx:80}
\begin{aligned}
\ddt{\Bx}
&= \inv{i\Hbar} \antisymmetric{\Bx}{H} \\
&= \inv{i\Hbar 2 m} \antisymmetric{\Bx}{\BPi^2} \\
&= \inv{i\Hbar 2 m} \antisymmetric{\Bx}{\Bp^2 – \frac{e}{c} \lr{ \BA \cdot \Bp
+ \Bp \cdot \BA } + \frac{e^2}{c^2} \BA^2 } \\
&= \inv{i\Hbar 2 m}
\lr{
\antisymmetric{\Bx}{\Bp^2}
– \frac{e}{c} \antisymmetric{\Bx}{ \BA \cdot \Bp + \Bp \cdot \BA }
}
.
\end{aligned}
\end{equation}

For the \( \Bp^2 \) commutator we have

\begin{equation}\label{eqn:gaugeTx:100}
\antisymmetric{x_r}{\Bp^2}
=
i \Hbar \PD{p_r}{\Bp^2}
=
2 i \Hbar p_r,
\end{equation}

or
\begin{equation}\label{eqn:gaugeTx:120}
\antisymmetric{\Bx}{\Bp^2}
=
2 i \Hbar \Bp.
\end{equation}

Computing the remaining commutator, we’ve got

\begin{equation}\label{eqn:gaugeTx:140}
\begin{aligned}
\antisymmetric{x_r}{\Bp \cdot \BA + \BA \cdot \Bp}
&= x_r p_s A_s – p_s A_s x_r \\
&\quad+ x_r A_s p_s – A_s p_s x_r \\
&= \lr{ \antisymmetric{x_r}{p_s} + p_s x_r } A_s – p_s A_s x_r \\
&\quad+ x_r A_s p_s – A_s \lr{ \antisymmetric{p_s}{x_r} + x_r p_s } \\
&= \antisymmetric{x_r}{p_s} A_s + {p_s A_s x_r – p_s A_s x_r} \\
&\quad+ {x_r A_s p_s – x_r A_s p_s} + A_s \antisymmetric{x_r}{p_s} \\
&= 2 i \Hbar \delta_{r s} A_s \\
&= 2 i \Hbar A_r,
\end{aligned}
\end{equation}

so

\begin{equation}\label{eqn:gaugeTx:160}
\antisymmetric{\Bx}{\Bp \cdot \BA + \BA \cdot \Bp} = 2 i \Hbar \BA.
\end{equation}

Assembling these results gives

\begin{equation}\label{eqn:gaugeTx:180}
\boxed{
\ddt{\Bx} = \inv{m} \lr{ \Bp – \frac{e}{c} \BA } = \inv{m} \BPi,
}
\end{equation}

as asserted in the text.

Kinetic Momentum commutators

\begin{equation}\label{eqn:gaugeTx:200}
\begin{aligned}
\antisymmetric{\Pi_r}{\Pi_s}
&=
\antisymmetric{p_r – e A_r/c}{p_s – e A_s/c} \\
&=
{\antisymmetric{p_r}{p_s}}
– \frac{e}{c} \lr{ \antisymmetric{p_r}{A_s} + \antisymmetric{A_r}{p_s}}
+ \frac{e^2}{c^2} {\antisymmetric{A_r}{A_s}} \\
&=
– \frac{e}{c} \lr{ (-i\Hbar) \PD{x_r}{A_s} + (i\Hbar) \PD{x_s}{A_r} } \\
&=
– \frac{i e \Hbar}{c} \lr{ -\PD{x_r}{A_s} + \PD{x_s}{A_r} } \\
&=
– \frac{i e \Hbar}{c} \epsilon_{t s r} B_t,
\end{aligned}
\end{equation}

or
\begin{equation}\label{eqn:gaugeTx:220}
\boxed{
\antisymmetric{\Pi_r}{\Pi_s}
=
\frac{i e \Hbar}{c} \epsilon_{r s t} B_t.
}
\end{equation}

Quantum Lorentz force

For the force equation we have

\begin{equation}\label{eqn:gaugeTx:240}
\begin{aligned}
m \frac{d^2 \Bx}{dt^2}
&= \ddt{\BPi} \\
&= \inv{i \Hbar} \antisymmetric{\BPi}{H} \\
&= \inv{i \Hbar 2 m } \antisymmetric{\BPi}{\BPi^2}
+ \inv{i \Hbar } \antisymmetric{\BPi}{e \phi}.
\end{aligned}
\end{equation}

For the \( \phi \) commutator consider one component

\begin{equation}\label{eqn:gaugeTx:260}
\begin{aligned}
\antisymmetric{\Pi_r}{e \phi}
&=
e \antisymmetric{p_r – \frac{e}{c} A_r}{\phi} \\
&=
e \antisymmetric{p_r}{\phi} \\
&=
e (-i\Hbar) \PD{x_r}{\phi},
\end{aligned}
\end{equation}

or
\begin{equation}\label{eqn:gaugeTx:280}
\inv{i \Hbar} \antisymmetric{\BPi}{e \phi}
=
– e \spacegrad \phi
=
e \BE.
\end{equation}

For the \( \BPi^2 \) commutator I initially did this the hard way (it took four notebook pages, plus two for a false start.) Realizing that I didn’t use \ref{eqn:gaugeTx:220} for that expansion was the clue to doing this more expediently.

Considering a single component

\begin{equation}\label{eqn:gaugeTx:300}
\begin{aligned}
\antisymmetric{\Pi_r}{\BPi^2}
&=
\antisymmetric{\Pi_r}{\Pi_s \Pi_s} \\
&=
\Pi_r \Pi_s \Pi_s – \Pi_s \Pi_s \Pi_r \\
&=
\lr{ \antisymmetric{\Pi_r}{\Pi_s} + {\Pi_s \Pi_r} }
\Pi_s
– \Pi_s
\lr{ \antisymmetric{\Pi_s}{\Pi_r} + {\Pi_r \Pi_s} } \\
&= i \Hbar \frac{e}{c} \epsilon_{r s t}
\lr{ B_t \Pi_s + \Pi_s B_t },
\end{aligned}
\end{equation}

or

\begin{equation}\label{eqn:gaugeTx:320}
\begin{aligned}
\inv{ i \Hbar 2 m} \antisymmetric{\BPi}{\BPi^2}
&= \frac{e}{2 m c } \epsilon_{r s t} \Be_r
\lr{ B_t \Pi_s + \Pi_s B_t } \\
&= \frac{e}{ 2 m c }
\lr{
\BPi \cross \BB
– \BB \cross \BPi
}.
\end{aligned}
\end{equation}

Putting all the pieces together we’ve got the quantum equivalent of the Lorentz force equation

\begin{equation}\label{eqn:gaugeTx:340}
\boxed{
m \frac{d^2 \Bx}{dt^2} = e \BE + \frac{e}{2 c} \lr{
\frac{d\Bx}{dt} \cross \BB
– \BB \cross \frac{d\Bx}{dt}
}.
}
\end{equation}

While this looks equivalent to the classical result, all the vectors here are Heisenberg picture operators dependent on position.

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

Quantum SHO ladder operators as a diagonal change of basis for the Heisenberg EOMs

August 19, 2015 phy1520 , , , , , , , , , , , , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

Many authors pull the definitions of the raising and lowering (or ladder) operators out of their butt with no attempt at motivation. This is pointed out nicely in [1] by Eli along with one justification based on factoring the Hamiltonian.

In [2] is a small exception to the usual presentation. In that text, these operators are defined as usual with no motivation. However, after the utility of these operators has been shown, the raising and lowering operators show up in a context that does provide that missing motivation as a side effect.
It doesn’t look like the author was trying to provide a motivation, but it can be interpreted that way.

When seeking the time evolution of Heisenberg-picture position and momentum operators, we will see that those solutions can be trivially expressed using the raising and lowering operators. No special tools nor black magic is required to find the structure of these operators. Unfortunately, we must first switch to both the Heisenberg picture representation of the position and momentum operators, and also employ the Heisenberg equations of motion. Neither of these last two fit into standard narrative of most introductory quantum mechanics treatments. We will also see that these raising and lowering “operators” could also be introduced in classical mechanics, provided we were attempting to solve the SHO system using the Hamiltonian equations of motion.

I’ll outline this route to finding the structure of the ladder operators below. Because these are encountered trying to solve the time evolution problem, I’ll first show a simpler way to solve that problem. Because that simpler method depends a bit on lucky observation and is somewhat unstructured, I’ll then outline a more structured procedure that leads to the ladder operators directly, also providing the solution to the time evolution problem as a side effect.

The starting point is the Heisenberg equations of motion. For a time independent Hamiltonian \( H \), and a Heisenberg operator \( A^{(H)} \), those equations are

\begin{equation}\label{eqn:harmonicOscDiagonalize:20}
\ddt{A^{(H)}} = \inv{i \Hbar} \antisymmetric{A^{(H)}}{H}.
\end{equation}

Here the Heisenberg operator \( A^{(H)} \) is related to the Schrodinger operator \( A^{(S)} \) by

\begin{equation}\label{eqn:harmonicOscDiagonalize:60}
A^{(H)} = U^\dagger A^{(S)} U,
\end{equation}

where \( U \) is the time evolution operator. For this discussion, we need only know that \( U \) commutes with \( H \), and do not need to know the specific structure of that operator. In particular, the Heisenberg equations of motion take the form

\begin{equation}\label{eqn:harmonicOscDiagonalize:80}
\begin{aligned}
\ddt{A^{(H)}}
&= \inv{i \Hbar}
\antisymmetric{A^{(H)}}{H} \\
&= \inv{i \Hbar}
\antisymmetric{U^\dagger A^{(S)} U}{H} \\
&= \inv{i \Hbar}
\lr{
U^\dagger A^{(S)} U H
– H U^\dagger A^{(S)} U
} \\
&= \inv{i \Hbar}
\lr{
U^\dagger A^{(S)} H U
– U^\dagger H A^{(S)} U
} \\
&= \inv{i \Hbar} U^\dagger \antisymmetric{A^{(S)}}{H} U.
\end{aligned}
\end{equation}

The Hamiltonian for the harmonic oscillator, with Schrodinger-picture position and momentum operators \( x, p \) is

\begin{equation}\label{eqn:harmonicOscDiagonalize:40}
H = \frac{p^2}{2m} + \inv{2} m \omega^2 x^2,
\end{equation}

so the equations of motions are

\begin{equation}\label{eqn:harmonicOscDiagonalize:100}
\begin{aligned}
\ddt{x^{(H)}}
&= \inv{i \Hbar} U^\dagger \antisymmetric{x}{H} U \\
&= \inv{i \Hbar} U^\dagger \antisymmetric{x}{\frac{p^2}{2m}} U \\
&= \inv{2 m i \Hbar} U^\dagger \lr{ i \Hbar \PD{p}{p^2} } U \\
&= \inv{m } U^\dagger p U \\
&= \inv{m } p^{(H)},
\end{aligned}
\end{equation}

and
\begin{equation}\label{eqn:harmonicOscDiagonalize:120}
\begin{aligned}
\ddt{p^{(H)}}
&= \inv{i \Hbar} U^\dagger \antisymmetric{p}{H} U \\
&= \inv{i \Hbar} U^\dagger \antisymmetric{p}{\inv{2} m \omega^2 x^2 } U \\
&= \frac{m \omega^2}{2 i \Hbar} U^\dagger \lr{ -i \Hbar \PD{x}{x^2} } U \\
&= -m \omega^2 U^\dagger x U \\
&= -m \omega^2 x^{(H)}.
\end{aligned}
\end{equation}

In the Heisenberg picture the equations of motion are precisely those of classical Hamiltonian mechanics, except that we are dealing with operators instead of scalars

\begin{equation}\label{eqn:harmonicOscDiagonalize:140}
\begin{aligned}
\ddt{p^{(H)}} &= -m \omega^2 x^{(H)} \\
\ddt{x^{(H)}} &= \inv{m } p^{(H)}.
\end{aligned}
\end{equation}

In the text the ladder operators are used to simplify the solution of these coupled equations, since they can decouple them. That’s not really required since we can solve them directly in matrix form with little work

\begin{equation}\label{eqn:harmonicOscDiagonalize:160}
\ddt{}
\begin{bmatrix}
p^{(H)} \\
x^{(H)}
\end{bmatrix}
=
\begin{bmatrix}
0 & -m \omega^2 \\
\inv{m} & 0
\end{bmatrix}
\begin{bmatrix}
p^{(H)} \\
x^{(H)}
\end{bmatrix},
\end{equation}

or, with length scaled variables

\begin{equation}\label{eqn:harmonicOscDiagonalize:180}
\begin{aligned}
\ddt{}
\begin{bmatrix}
\frac{p^{(H)}}{m \omega} \\
x^{(H)}
\end{bmatrix}
&=
\begin{bmatrix}
0 & -\omega \\
\omega & 0
\end{bmatrix}
\begin{bmatrix}
\frac{p^{(H)}}{m \omega} \\
x^{(H)}
\end{bmatrix} \\
&=
-i \omega
\begin{bmatrix} 0 & -i \\ i & 0 \\ \end{bmatrix}
\begin{bmatrix}
\frac{p^{(H)}}{m \omega} \\
x^{(H)}
\end{bmatrix} \\
&=
-i \omega
\sigma_y
\begin{bmatrix}
\frac{p^{(H)}}{m \omega} \\
x^{(H)}
\end{bmatrix}.
\end{aligned}
\end{equation}

Writing \( y = \begin{bmatrix} \frac{p^{(H)}}{m \omega} \\ x^{(H)} \end{bmatrix} \), the solution can then be written immediately as

\begin{equation}\label{eqn:harmonicOscDiagonalize:200}
\begin{aligned}
y(t)
&=
\exp\lr{ -i \omega \sigma_y t } y(0) \\
&=
\lr{ \cos \lr{ \omega t } I – i \sigma_y \sin\lr{ \omega t } } y(0) \\
&=
\begin{bmatrix}
\cos\lr{ \omega t } & \sin\lr{ \omega t } \\
-\sin\lr{ \omega t } & \cos\lr{ \omega t }
\end{bmatrix}
y(0),
\end{aligned}
\end{equation}

or

\begin{equation}\label{eqn:harmonicOscDiagonalize:220}
\begin{aligned}
\frac{p^{(H)}(t)}{m \omega} &= \cos\lr{ \omega t } \frac{p^{(H)}(0)}{m \omega} + \sin\lr{ \omega t } x^{(H)}(0) \\
x^{(H)}(t) &= -\sin\lr{ \omega t } \frac{p^{(H)}(0)}{m \omega} + \cos\lr{ \omega t } x^{(H)}(0).
\end{aligned}
\end{equation}

This solution depends on being lucky enough to recognize that the matrix has a Pauli matrix as a factor (which squares to unity, and allows the exponential to be evaluated easily.)

If we hadn’t been that observant, then the first tool we’d have used instead would have been to diagonalize the matrix. For such diagonalization, it’s natural to work in completely dimensionless variables. Such a non-dimensionalisation can be had by defining

\begin{equation}\label{eqn:harmonicOscDiagonalize:240}
x_0 = \sqrt{\frac{\Hbar}{m \omega}},
\end{equation}

and dividing the working (operator) variables through by those values. Let \( z = \inv{x_0} y \), and \( \tau = \omega t \) so that the equations of motion are

\begin{equation}\label{eqn:harmonicOscDiagonalize:260}
\frac{dz}{d\tau}
=
\begin{bmatrix}
0 & -1 \\
1 & 0
\end{bmatrix}
z.
\end{equation}

This matrix can be diagonalized as

\begin{equation}\label{eqn:harmonicOscDiagonalize:280}
A
=
\begin{bmatrix}
0 & -1 \\
1 & 0
\end{bmatrix}
=
V
\begin{bmatrix}
i & 0 \\
0 & -i
\end{bmatrix}
V^{-1},
\end{equation}

where

\begin{equation}\label{eqn:harmonicOscDiagonalize:300}
V =
\inv{\sqrt{2}}
\begin{bmatrix}
i & -i \\
1 & 1
\end{bmatrix}.
\end{equation}

The equations of motion can now be written

\begin{equation}\label{eqn:harmonicOscDiagonalize:320}
\frac{d}{d\tau} \lr{ V^{-1} z } =
\begin{bmatrix}
i & 0 \\
0 & -i
\end{bmatrix}
\lr{ V^{-1} z }.
\end{equation}

This final change of variables \( V^{-1} z \) decouples the system as desired. Expanding that gives

\begin{equation}\label{eqn:harmonicOscDiagonalize:340}
\begin{aligned}
V^{-1} z
&=
\inv{\sqrt{2}}
\begin{bmatrix}
-i & 1 \\
i & 1
\end{bmatrix}
\begin{bmatrix}
\frac{p^{(H)}}{x_0 m \omega} \\
\frac{x^{(H)}}{x_0}
\end{bmatrix} \\
&=
\inv{\sqrt{2} x_0}
\begin{bmatrix}
-i \frac{p^{(H)}}{m \omega} + x^{(H)} \\
i \frac{p^{(H)}}{m \omega} + x^{(H)}
\end{bmatrix} \\
&=
\begin{bmatrix}
a^\dagger \\
a
\end{bmatrix},
\end{aligned}
\end{equation}

where
\begin{equation}\label{eqn:harmonicOscDiagonalize:n}
\begin{aligned}
a^\dagger &= \sqrt{\frac{m \omega}{2 \Hbar}} \lr{ -i \frac{p^{(H)}}{m \omega} + x^{(H)} } \\
a &= \sqrt{\frac{m \omega}{2 \Hbar}} \lr{ i \frac{p^{(H)}}{m \omega} + x^{(H)} }.
\end{aligned}
\end{equation}

Lo and behold, we have the standard form of the raising and lowering operators, and can write the system equations as

\begin{equation}\label{eqn:harmonicOscDiagonalize:360}
\begin{aligned}
\ddt{a^\dagger} &= i \omega a^\dagger \\
\ddt{a} &= -i \omega a.
\end{aligned}
\end{equation}

It is actually a bit fluky that this matched exactly, since we could have chosen eigenvectors that differ by constant phase factors, like

\begin{equation}\label{eqn:harmonicOscDiagonalize:380}
V = \inv{\sqrt{2}}
\begin{bmatrix}
i e^{i\phi} & -i e^{i \psi} \\
1 e^{i\phi} & e^{i \psi}
\end{bmatrix},
\end{equation}

so

\begin{equation}\label{eqn:harmonicOscDiagonalize:341}
\begin{aligned}
V^{-1} z
&=
\frac{e^{-i(\phi + \psi)}}{\sqrt{2}}
\begin{bmatrix}
-i e^{i\psi} & e^{i \psi} \\
i e^{i\phi} & e^{i \phi}
\end{bmatrix}
\begin{bmatrix}
\frac{p^{(H)}}{x_0 m \omega} \\
\frac{x^{(H)}}{x_0}
\end{bmatrix} \\
&=
\inv{\sqrt{2} x_0}
\begin{bmatrix}
-i e^{i\phi} \frac{p^{(H)}}{m \omega} + e^{i\phi} x^{(H)} \\
i e^{i\psi} \frac{p^{(H)}}{m \omega} + e^{i\psi} x^{(H)}
\end{bmatrix} \\
&=
\begin{bmatrix}
e^{i\phi} a^\dagger \\
e^{i\psi} a
\end{bmatrix}.
\end{aligned}
\end{equation}

To make the resulting pairs of operators Hermitian conjugates, we’d want to constrain those constant phase factors by setting \( \phi = -\psi \). If we were only interested in solving the time evolution problem no such additional constraints are required.

The raising and lowering operators are seen to naturally occur when seeking the solution of the Heisenberg equations of motion. This is found using the standard technique of non-dimensionalisation and then seeking a change of basis that diagonalizes the system matrix. Because the Heisenberg equations of motion are identical to the classical Hamiltonian equations of motion in this case, what we call the raising and lowering operators in quantum mechanics could also be utilized in the classical simple harmonic oscillator problem. However, in a classical context we wouldn’t have a justification to call this more than a change of basis.

References

[1] Eli Lansey. The Quantum Harmonic Oscillator Ladder Operators, 2009. URL http://behindtheguesses.blogspot.ca/2009/03/quantum-harmonic-oscillator-ladder.html. [Online; accessed 18-August-2015].

[2] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics, chapter {Time Development of the Oscillator}. Pearson Higher Ed, 2014.