math and physics play

PHY2403H Quantum Field Theory. Lecture 4: Scalar action, least action principle, Euler-Lagrange equations for a field, canonical quantization. Taught by Prof. Erich Poppitz

September 23, 2018 phy2403 , , , , , , , , , , , , , , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

DISCLAIMER: Very rough notes from class. May have some additional side notes, but otherwise probably barely edited.

These are notes for the UofT course PHY2403H, Quantum Field Theory I, taught by Prof. Erich Poppitz fall 2018.

Principles (cont.)

  • Lorentz (Poincar\’e : Lorentz and spacetime translations)
  • locality
  • dimensional analysis
  • gauge invariance

These are the requirements for an action. We postulated an action that had the form
\begin{equation}\label{eqn:qftLecture4:20}
\int d^d x \partial_\mu \phi \partial^\mu \phi,
\end{equation}
called the “Kinetic term”, which mimics \( \int dt \dot{q}^2 \) that we’d see in quantum or classical mechanics. In principle there exists an infinite number of local Poincar\’e invariant terms that we can write. Examples:

  • \( \partial_\mu \phi \partial^\mu \phi \)
  • \( \partial_\mu \phi \partial_\nu \partial^\nu \partial^\mu \phi \)
  • \( \lr{\partial_\mu \phi \partial^\mu \phi}^2 \)
  • \( f(\phi) \partial_\mu \phi \partial^\mu \phi \)
  • \( f(\phi, \partial_\mu \phi \partial^\mu \phi) \)
  • \( V(\phi) \)

It turns out that nature (i.e. three spatial dimensions and one time dimension) is described by a finite number of terms. We will now utilize dimensional analysis to determine some of the allowed forms of the action for scalar field theories in \( d = 2, 3, 4, 5 \) dimensions. Even though the real world is only \( d = 4 \), some of the \( d < 4 \) theories are relevant in condensed matter studies, and \( d = 5 \) is just for fun (but also applies to string theories.)

With \( [x] \sim \inv{M} \) in natural units, we must define \([\phi]\) such that the kinetic term is dimensionless in d spacetime dimensions

\begin{equation}\label{eqn:qftLecture4:40}
\begin{aligned}
[d^d x] &\sim \inv{M^d} \\
[\partial_\mu] &\sim M
\end{aligned}
\end{equation}

so it must be that
\begin{equation}\label{eqn:qftLecture4:60}
[\phi] = M^{(d-2)/2}
\end{equation}

It will be easier to characterize the dimensionality of any given term by the power of the mass units, that is

\begin{equation}\label{eqn:qftLecture4:80}
\begin{aligned}
[\text{mass}] &= 1 \\
[d^d x] &= -d \\
[\partial_\mu] &= 1 \\
[\phi] &= (d-2)/2 \\
[S] &= 0.
\end{aligned}
\end{equation}
Since the action is
\begin{equation}\label{eqn:qftLecture4:100}
S = \int d^d x \lr{ \LL(\phi, \partial_\mu \phi) },
\end{equation}
and because action had dimensions of \( \Hbar \), so in natural units, it must be dimensionless, the Lagrangian density dimensions must be \( [d] \). We will abuse language in QFT and call the Lagrangian density the Lagrangian.

\( d = 2 \)

Because \( [\partial_\mu \phi \partial^\mu \phi ] = 2 \), the scalar field must be dimension zero, or in symbols
\begin{equation}\label{eqn:qftLecture4:120}
[\phi] = 0.
\end{equation}
This means that introducing any function \( f(\phi) = 1 + a \phi + b\phi^2 + c \phi^3 + \cdots \) is also dimensionless, and
\begin{equation}\label{eqn:qftLecture4:140}
[f(\phi) \partial_\mu \phi \partial^\mu \phi ] = 2,
\end{equation}
for any \( f(\phi) \). Another implication of this is that the a potential term in the Lagrangian \( [V(\phi)] = 0 \) needs a coupling constant of dimension 2. Letting \( \mu \) have mass dimensions, our Lagrangian must have the form
\begin{equation}\label{eqn:qftLecture4:160}
f(\phi) \partial_\mu \phi \partial^\mu \phi + \mu^2 V(\phi).
\end{equation}
An infinite number of coupling constants of positive mass dimensions for \( V(\phi) \) are also allowed. If we have higher order derivative terms, then we need to compensate for the negative mass dimensions. Example (still for \( d = 2 \)).
\begin{equation}\label{eqn:qftLecture4:180}
\LL =
f(\phi) \partial_\mu \phi \partial^\mu \phi + \mu^2 V(\phi) + \inv{{\mu’}^2}\partial_\mu \phi \partial_\nu \partial^\nu \partial^\mu \phi + \lr{ \partial_\mu \phi \partial^\mu \phi }^2 \inv{\tilde{\mu}^2}.
\end{equation}
The last two terms, called \underline{couplings} (i.e. any non-kinetic term), are examples of terms with negative mass dimension. There is an infinite number of those in any theory in any dimension.

Definitions

  • Couplings that are dimensionless are called (classically) marginal.
  • Couplings that have positive mass dimension are called (classically) relevant.
  • Couplings that have negative mass dimension are called (classically) irrelevant.

In QFT we are generally interested in the couplings that are measurable at long distances for some given energy. Classically irrelevant theories are generally not interesting in \( d > 2 \), so we are very lucky that we don’t live in three dimensional space. This means that we can get away with a finite number of classically marginal and relevant couplings in 3 or 4 dimensions. This was mentioned in the Wilczek’s article referenced in the class forum [1]\footnote{There’s currently more in that article that I don’t understand than I do, so it is hard to find it terribly illuminating.}

Long distance physics in any dimension is described by the marginal and relevant couplings. The irrelevant couplings die off at low energy. In two dimensions, a priori, an infinite number of marginal and relevant couplings are possible. 2D is a bad place to live!

\( d = 3 \)

Now we have
\begin{equation}\label{eqn:qftLecture4:200}
[\phi] = \inv{2}
\end{equation}
so that
\begin{equation}\label{eqn:qftLecture4:220}
[\partial_\mu \phi \partial^\mu \phi] = 3.
\end{equation}

A 3D Lagrangian could have local terms such as
\begin{equation}\label{eqn:qftLecture4:240}
\LL = \partial_\mu \phi \partial^\mu \phi + m^2 \phi^2 + \mu^{3/2} \phi^3 + \mu’ \phi^4
+ \lr{\mu”}{1/2} \phi^5
+ \lambda \phi^6.
\end{equation}
where \( m, \mu, \mu” \) all have mass dimensions, and \( \lambda \) is dimensionless. i.e. \( m, \mu, \mu” \) are relevant, and \( \lambda \) marginal. We stop at the sixth power, since any power after that will be irrelevant.

\( d = 4 \)

Now we have
\begin{equation}\label{eqn:qftLecture4:260}
[\phi] = 1
\end{equation}
so that
\begin{equation}\label{eqn:qftLecture4:280}
[\partial_\mu \phi \partial^\mu \phi] = 4.
\end{equation}

In this number of dimensions \( \phi^k \partial_\mu \phi \partial^\mu \) is an irrelevant coupling.

A 4D Lagrangian could have local terms such as
\begin{equation}\label{eqn:qftLecture4:300}
\LL = \partial_\mu \phi \partial^\mu \phi + m^2 \phi^2 + \mu \phi^3 + \lambda \phi^4.
\end{equation}
where \( m, \mu \) have mass dimensions, and \( \lambda \) is dimensionless. i.e. \( m, \mu \) are relevant, and \( \lambda \) is marginal.

\( d = 5 \)

Now we have
\begin{equation}\label{eqn:qftLecture4:320}
[\phi] = \frac{3}{2},
\end{equation}
so that
\begin{equation}\label{eqn:qftLecture4:340}
[\partial_\mu \phi \partial^\mu \phi] = 5.
\end{equation}

A 5D Lagrangian could have local terms such as
\begin{equation}\label{eqn:qftLecture4:360}
\LL = \partial_\mu \phi \partial^\mu \phi + m^2 \phi^2 + \sqrt{\mu} \phi^3 + \inv{\mu’} \phi^4.
\end{equation}
where \( m, \mu, \mu’ \) all have mass dimensions. In 5D there are no marginal couplings. Dimension 4 is the last dimension where marginal couplings exist. In condensed matter physics 4D is called the “upper critical dimension”.

From the point of view of particle physics, all the terms in the Lagrangian must be the ones that are relevant at long distances.

Least action principle (classical field theory).

Now we want to study 4D scalar theories. We have some action
\begin{equation}\label{eqn:qftLecture4:380}
S[\phi] = \int d^4 x \LL(\phi, \partial_\mu \phi).
\end{equation}

Let’s keep an example such as the following in mind
\begin{equation}\label{eqn:qftLecture4:400}
\LL = \underbrace{\inv{2} \partial_\mu \phi \partial^\mu \phi}_{\text{Kinetic term}} – \underbrace{m^2 \phi – \lambda \phi^4}_{\text{all relevant and marginal couplings}}.
\end{equation}
The even powers can be justified by assuming there is some symmetry that kills the odd powered terms.

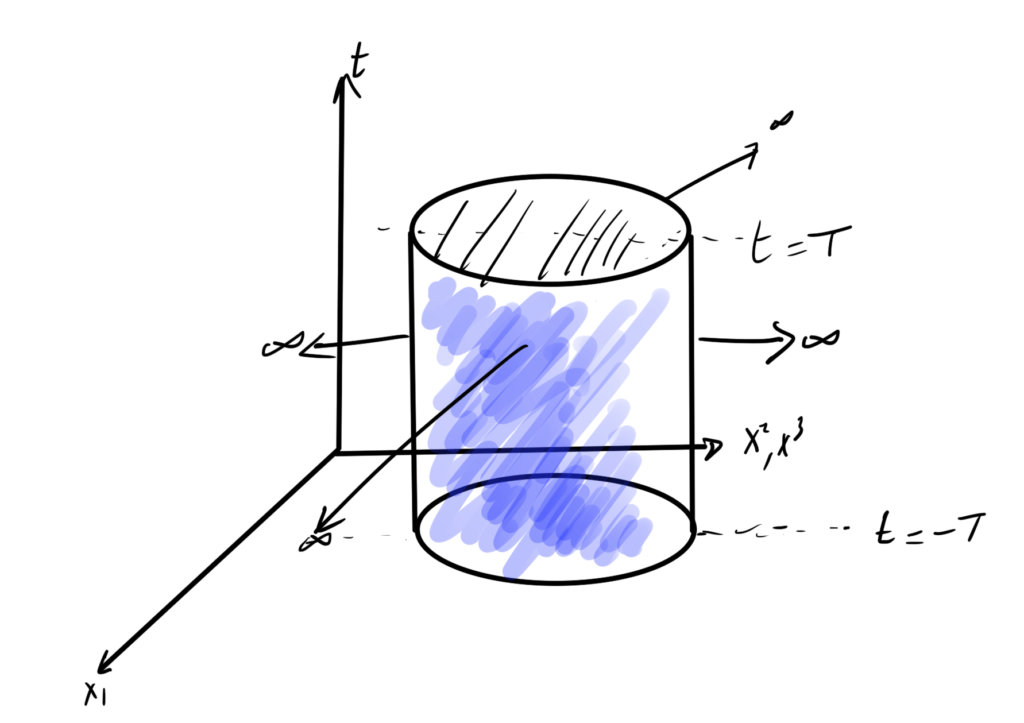
fig. 1. Cylindrical spacetime boundary.

We will be integrating over a space time region such as that depicted in fig. 1, where a cylindrical spatial cross section is depicted that we allow to tend towards infinity. We demand that the field is fixed on the infinite spatial boundaries. The easiest way to demand that the field dies off on the spatial boundaries, that is
\begin{equation}\label{eqn:qftLecture4:420}
\lim_{\Abs{\Bx} \rightarrow \infty} \phi(\Bx) \rightarrow 0.
\end{equation}
The functional \( \phi(\Bx, t) \) that obeys the boundary condition as stated extremizes \( S[\phi] \).

Extremizing the action means that we seek \( \phi(\Bx, t) \)
\begin{equation}\label{eqn:qftLecture4:440}
\delta S[\phi] = 0 = S[\phi + \delta \phi] – S[\phi].
\end{equation}

How do we compute the variation?
\begin{equation}\label{eqn:qftLecture4:460}
\begin{aligned}
\delta S
&= \int d^d x \lr{ \LL(\phi + \delta \phi, \partial_\mu \phi + \partial_\mu \delta \phi) – \LL(\phi, \partial_\mu \phi) } \\
&= \int d^d x \lr{ \PD{\phi}{\LL} \delta \phi + \PD{(\partial_mu \phi)}{\LL} (\partial_\mu \delta \phi) } \\
&= \int d^d x \lr{ \PD{\phi}{\LL} \delta \phi
+ \partial_\mu \lr{ \PD{(\partial_mu \phi)}{\LL} \delta \phi}
– \lr{ \partial_\mu \PD{(\partial_mu \phi)}{\LL} } \delta \phi
} \\
&=
\int d^d x
\delta \phi
\lr{ \PD{\phi}{\LL}
– \partial_\mu \PD{(\partial_mu \phi)}{\LL} }
+ \int d^3 \sigma_\mu \lr{ \PD{(\partial_\mu \phi)}{\LL} \delta \phi }
\end{aligned}
\end{equation}

If we are explicit about the boundary term, we write it as
\begin{equation}\label{eqn:qftLecture4:480}
\int dt d^3 \Bx \partial_t \lr{ \PD{(\partial_t \phi)}{\LL} \delta \phi }
– \spacegrad \cdot \lr{ \PD{(\spacegrad \phi)}{\LL} \delta \phi }
=
\int d^3 \Bx \evalrange{ \PD{(\partial_t \phi)}{\LL} \delta \phi }{t = -T}{t = T}
– \int dt d^2 \BS \cdot \lr{ \PD{(\spacegrad \phi)}{\LL} \delta \phi }.
\end{equation}
but \( \delta \phi = 0 \) at \( t = \pm T \) and also at the spatial boundaries of the integration region.

This leaves
\begin{equation}\label{eqn:qftLecture4:500}
\delta S[\phi] = \int d^d x \delta \phi
\lr{ \PD{\phi}{\LL} – \partial_\mu \PD{(\partial_mu \phi)}{\LL} } = 0 \forall \delta \phi.
\end{equation}
That is

\begin{equation}\label{eqn:qftLecture4:540}
\boxed{
\PD{\phi}{\LL} – \partial_\mu \PD{(\partial_mu \phi)}{\LL} = 0.
}
\end{equation}

This are the Euler-Lagrange equations for a single scalar field.

Returning to our sample scalar Lagrangian
\begin{equation}\label{eqn:qftLecture4:560}
\LL = \inv{2} \partial_\mu \phi \partial^\mu \phi – \inv{2} m^2 \phi^2 – \frac{\lambda}{4} \phi^4.
\end{equation}
This example is related to the Ising model which has a \( \phi \rightarrow -\phi \) symmetry. Applying the Euler-Lagrange equations, we have
\begin{equation}\label{eqn:qftLecture4:580}
\PD{\phi}{\LL} = -m^2 \phi – \lambda \phi^3,
\end{equation}
and
\begin{equation}\label{eqn:qftLecture4:600}
\begin{aligned}
\PD{(\partial_\mu \phi)}{\LL}
&=
\PD{(\partial_\mu \phi)}{} \lr{
\inv{2} \partial_\nu \phi \partial^\nu \phi } \\
&=
\inv{2} \partial^\nu \phi
\PD{(\partial_\mu \phi)}{}
\partial_\nu \phi
+
\inv{2} \partial_\nu \phi
\PD{(\partial_\mu \phi)}{}
\partial_\alpha \phi g^{\nu\alpha} \\
&=
\inv{2} \partial^\mu \phi
+
\inv{2} \partial_\nu \phi g^{\nu\mu} \\
&=
\partial^\mu \phi
\end{aligned}
\end{equation}
so we have
\begin{equation}\label{eqn:qftLecture4:620}
\begin{aligned}
0
&=
\PD{\phi}{\LL} -\partial_\mu
\PD{(\partial_\mu \phi)}{\LL} \\
&=
-m^2 \phi – \lambda \phi^3 – \partial_\mu \partial^\mu \phi.
\end{aligned}
\end{equation}

For \( \lambda = 0 \), the free field theory limit, this is just
\begin{equation}\label{eqn:qftLecture4:640}
\partial_\mu \partial^\mu \phi + m^2 \phi = 0.
\end{equation}
Written out from the observer frame, this is
\begin{equation}\label{eqn:qftLecture4:660}
(\partial_t)^2 \phi – \spacegrad^2 \phi + m^2 \phi = 0.
\end{equation}

With a non-zero mass term
\begin{equation}\label{eqn:qftLecture4:680}
\lr{ \partial_t^2 – \spacegrad^2 + m^2 } \phi = 0,
\end{equation}
is called the Klein-Gordan equation.

If we also had \( m = 0 \) we’d have
\begin{equation}\label{eqn:qftLecture4:700}
\lr{ \partial_t^2 – \spacegrad^2 } \phi = 0,
\end{equation}
which is the wave equation (for a massless free field). This is also called the D’Alembert equation, which is familiar from electromagnetism where we have
\begin{equation}\label{eqn:qftLecture4:720}
\begin{aligned}
\lr{ \partial_t^2 – \spacegrad^2 } \BE &= 0 \\
\lr{ \partial_t^2 – \spacegrad^2 } \BB &= 0,
\end{aligned}
\end{equation}
in a source free region.

Canonical quantization.

\begin{equation}\label{eqn:qftLecture4:740}
\LL = \inv{2} \dot{q} – \frac{\omega^2}{2} q^2
\end{equation}
This has solution \(\ddot{q} = – \omega^2 q\).

Let
\begin{equation}\label{eqn:qftLecture4:760}
p = \PD{\dot{q}}{\LL} = \dot{q}
\end{equation}
\begin{equation}\label{eqn:qftLecture4:780}
H(p,q) = \evalbar{p \dot{q} – \LL}{\dot{q}(p, q)}
= p p – \inv{2} p^2 + \frac{\omega^2}{2} q^2 = \frac{p^2}{2} + \frac{\omega^2}{2} q^2
\end{equation}

In QM we quantize by mapping Poisson brackets to commutators.
\begin{equation}\label{eqn:qftLecture4:800}
\antisymmetric{\hatp}{\hat{q}} = -i
\end{equation}
One way to represent is to say that states are \( \Psi(\hat{q}) \), a wave function, \( \hat{q} \) acts by \( q \)
\begin{equation}\label{eqn:qftLecture4:820}
\hat{q} \Psi = q \Psi(q)
\end{equation}
With
\begin{equation}\label{eqn:qftLecture4:840}
\hatp = -i \PD{q}{},
\end{equation}
so
\begin{equation}\label{eqn:qftLecture4:860}
\antisymmetric{ -i \PD{q}{} } { q} = -i
\end{equation}

Let’s introduce an explicit space time split. We’ll write
\begin{equation}\label{eqn:qftLecture4:880}
L = \int d^3 x \lr{
\inv{2} (\partial_0 \phi(\Bx, t))^2 – \inv{2} \lr{ \spacegrad \phi(\Bx, t) }^2 – \frac{m^2}{2} \phi
},
\end{equation}
so that the action is
\begin{equation}\label{eqn:qftLecture4:900}
S = \int dt L.
\end{equation}
The dynamical variables are \( \phi(\Bx) \). We define
\begin{equation}\label{eqn:qftLecture4:920}
\begin{aligned}
\pi(\Bx, t) = \frac{\delta L}{\delta (\partial_0 \phi(\Bx, t))}
&=
\partial_0 \phi(\Bx, t) \\
&=
\dot{\phi}(\Bx, t),
\end{aligned}
\end{equation}
called the canonical momentum, or the momentum conjugate to \( \phi(\Bx, t) \). Why \( \delta \)? Has to do with an implicit Dirac function to eliminate the integral?

\begin{equation}\label{eqn:qftLecture4:940}
\begin{aligned}
H
&= \int d^3 x \evalbar{\lr{ \pi(\bar{\Bx}, t) \dot{\phi}(\bar{\Bx}, t) – L }}{\dot{\phi}(\bar{\Bx}, t) = \pi(x, t) } \\
&= \int d^3 x \lr{ (\pi(\Bx, t))^2 – \inv{2} (\pi(\Bx, t))^2 + \inv{2} (\spacegrad \phi)^2 + \frac{m}{2} \phi^2 },
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:qftLecture4:960}
H
= \int d^3 x \lr{ \inv{2} (\pi(\Bx, t))^2 + \inv{2} (\spacegrad \phi(\Bx, t))^2 + \frac{m}{2} (\phi(\Bx, t))^2 }
\end{equation}

In analogy to the momentum, position commutator in QM
\begin{equation}\label{eqn:qftLecture4:1000}
\antisymmetric{\hat{p}_i}{\hat{q}_j} = -i \delta_{ij},
\end{equation}
we “quantize” the scalar field theory by promoting \( \pi, \phi \) to operators and insisting that they also obey a commutator relationship
\begin{equation}\label{eqn:qftLecture4:980}
\antisymmetric{\pi(\Bx, t)}{\phi(\By, t)} = -i \delta^3(\Bx – \By).
\end{equation}

References

[1] Frank Wilczek. Fundamental constants. arXiv preprint arXiv:0708.4361, 2007. URL https://arxiv.org/abs/0708.4361.

PHY2403H Quantum Field Theory. Lecture 3: Lorentz transformations and a scalar action. Taught by Prof. Erich Poppitz

September 18, 2018 phy2403 , ,

[Click here for a PDF of this post with nicer formatting]

DISCLAIMER: Very rough notes from class. Some additional side notes, but otherwise barely edited.

These are notes for the UofT course PHY2403H, Quantum Field Theory, taught by Prof. Erich Poppitz.

Determinant of Lorentz transformations

We require that Lorentz transformations leave the dot product invariant, that is \( x \cdot y = x’ \cdot y’ \), or
\begin{equation}\label{eqn:qftLecture3:20}
x^\mu g_{\mu\nu} y^\nu = {x’}^\mu g_{\mu\nu} {y’}^\nu.
\end{equation}
Explicitly, with coordinate transformations
\begin{equation}\label{eqn:qftLecture3:40}
\begin{aligned}
{x’}^\mu &= {\Lambda^\mu}_\rho x^\rho \\
{y’}^\mu &= {\Lambda^\mu}_\rho y^\rho
\end{aligned}
\end{equation}
such a requirement is equivalent to demanding that
\begin{equation}\label{eqn:qftLecture3:500}
\begin{aligned}
x^\mu g_{\mu\nu} y^\nu
&=
{\Lambda^\mu}_\rho x^\rho
g_{\mu\nu}
{\Lambda^\nu}_\kappa y^\kappa \\
&=
x^\mu
{\Lambda^\alpha}_\mu
g_{\alpha\beta}
{\Lambda^\beta}_\nu
y^\nu,
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:qftLecture3:60}
g_{\mu\nu}
=
{\Lambda^\alpha}_\mu
g_{\alpha\beta}
{\Lambda^\beta}_\nu
\end{equation}

multiplying by the inverse we find
\begin{equation}\label{eqn:qftLecture3:200}
\begin{aligned}
g_{\mu\nu}
{\lr{\Lambda^{-1}}^\nu}_\lambda
&=
{\Lambda^\alpha}_\mu
g_{\alpha\beta}
{\Lambda^\beta}_\nu
{\lr{\Lambda^{-1}}^\nu}_\lambda \\
&=
{\Lambda^\alpha}_\mu
g_{\alpha\lambda} \\
&=
g_{\lambda\alpha}
{\Lambda^\alpha}_\mu.
\end{aligned}
\end{equation}
This is now amenable to expressing in matrix form
\begin{equation}\label{eqn:qftLecture3:220}
\begin{aligned}
(G \Lambda^{-1})_{\mu\lambda}
&=
(G \Lambda)_{\lambda\mu} \\
&=
((G \Lambda)^\T)_{\mu\lambda} \\
&=
(\Lambda^\T G)_{\mu\lambda},
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:qftLecture3:80}
G \Lambda^{-1}
=
(G \Lambda)^\T.
\end{equation}

Taking determinants (using the normal identities for products of determinants, determinants of transposes and inverses), we find
\begin{equation}\label{eqn:qftLecture3:100}
det(G)
det(\Lambda^{-1})
=
det(G) det(\Lambda),
\end{equation}
or
\begin{equation}\label{eqn:qftLecture3:120}
det(\Lambda)^2 = 1,
\end{equation}
or
\( det(\Lambda)^2 = \pm 1 \). We will generally ignore the case of reflections in spacetime that have a negative determinant.

Smart-alec Peeter pointed out after class last time that we can do the same thing easier in matrix notation
\begin{equation}\label{eqn:qftLecture3:140}
\begin{aligned}
x’ &= \Lambda x \\
y’ &= \Lambda y
\end{aligned}
\end{equation}
where
\begin{equation}\label{eqn:qftLecture3:160}
\begin{aligned}
x’ \cdot y’
&=
(x’)^\T G y’ \\
&=
x^\T \Lambda^\T G \Lambda y,
\end{aligned}
\end{equation}
which we require to be \( x \cdot y = x^\T G y \) for all four vectors \( x, y \), that is
\begin{equation}\label{eqn:qftLecture3:180}
\Lambda^\T G \Lambda = G.
\end{equation}
We can find the result \ref{eqn:qftLecture3:120} immediately without having to first translate from index notation to matrices.

Field theory

The electrostatic potential is an example of a scalar field \( \phi(\Bx) \) unchanged by SO(3) rotations
\begin{equation}\label{eqn:qftLecture3:240}
\Bx \rightarrow \Bx’ = O \Bx,
\end{equation}
that is
\begin{equation}\label{eqn:qftLecture3:260}
\phi'(\Bx’) = \phi(\Bx).
\end{equation}
Here \( \phi'(\Bx’) \) is the value of the (electrostatic) scalar potential in a primed frame.

However, the electrostatic field is not invariant under Lorentz transformation.
We postulate that there is some scalar field
\begin{equation}\label{eqn:qftLecture3:280}
\phi'(x’) = \phi(x),
\end{equation}
where \( x’ = \Lambda x \) is an SO(1,3) transformation. There are actually no stable particles (fields that persist at long distances) described by Lorentz scalar fields, although there are some unstable scalar fields such as the Higgs, Pions, and Kaons. However, much of our homework and discussion will be focused on scalar fields, since they are the easiest to start with.

We need to first understand how derivatives \( \partial_\mu \phi(x) \) transform. Using the chain rule
\begin{equation}\label{eqn:qftLecture3:300}
\begin{aligned}
\PD{x^\mu}{\phi(x)}
&=
\PD{x^\mu}{\phi'(x’)} \\
&=
\PD{{x’}^\nu}{\phi'(x’)}
\PD{{x}^\mu}{{x’}^\nu} \\
&=
\PD{{x’}^\nu}{\phi'(x’)}
\partial_\mu \lr{
{\Lambda^\nu}_\rho x^\rho
} \\
&=
\PD{{x’}^\nu}{\phi'(x’)}
{\Lambda^\nu}_\mu \\
&=
\PD{{x’}^\nu}{\phi(x)}
{\Lambda^\nu}_\mu.
\end{aligned}
\end{equation}
Multiplying by the inverse \( {\lr{\Lambda^{-1}}^\mu}_\kappa \) we get
\begin{equation}\label{eqn:qftLecture3:320}
\PD{{x’}^\kappa}{}
=
{\lr{\Lambda^{-1}}^\mu}_\kappa \PD{x^\mu}{}
\end{equation}

This should be familiar to you, and is an analogue of the transformation of the
\begin{equation}\label{eqn:qftLecture3:340}
d\Br \cdot \spacegrad_\Br
=
d\Br’ \cdot \spacegrad_{\Br’}.
\end{equation}

Actions

We will start with a classical action, and quantize to determine a QFT. In mechanics we have the particle position \( q(t) \), which is a classical field in 1+0 time and space dimensions. Our action is
\begin{equation}\label{eqn:qftLecture3:360}
S
= \int dt \LL(t)
= \int dt \lr{
\inv{2} \dot{q}^2 – V(q)
}.
\end{equation}
This action depends on the position of the particle that is local in time. You could imagine that we have a more complex action where the action depends on future or past times
\begin{equation}\label{eqn:qftLecture3:380}
S
= \int dt’ q(t’) K( t’ – t ),
\end{equation}
but we don’t seem to find such actions in classical mechanics.

Principles determining the form of the action.

  • relativity (action is invariant under Lorentz transformation)
  • locality (action depends on fields and the derivatives at given \((t, \Bx)\).
  • Gauge principle (the action should be invariant under gauge transformation). We won’t discuss this in detail right now since we will start with studying scalar fields.
    Recall that for Maxwell’s equations a gauge transformation has the form
    \begin{equation}\label{eqn:qftLecture3:520}
    \phi \rightarrow \phi + \dot{\chi}, \BA \rightarrow \BA – \spacegrad \chi.
    \end{equation}

Suppose we have a real scalar field \( \phi(x) \) where \( x \in \mathbb{R}^{1,d-1} \). We will be integrating over space and time \( \int dt d^{d-1} x \) which we will write as \( \int d^d x \). Our action is
\begin{equation}\label{eqn:qftLecture3:400}
S = \int d^d x \lr{ \text{Some action density to be determined } }
\end{equation}
The analogue of \( \dot{q}^2 \) is
\begin{equation}\label{eqn:qftLecture3:420}
\begin{aligned}
\lr{ \PD{x^\mu}{\phi} }
\lr{ \PD{x^\nu}{\phi} }
g^{\mu\nu}
&=
(\partial_\mu \phi) (\partial_\nu \phi) g^{\mu\nu} \\
&= \partial^\mu \phi \partial_\mu \phi.
\end{aligned}
\end{equation}
This has both time and spatial components, that is
\begin{equation}\label{eqn:qftLecture3:440}
\partial^\mu \phi \partial_\mu \phi =
\dotphi^2 – (\spacegrad \phi)^2,
\end{equation}
so the desired simplest scalar action is
\begin{equation}\label{eqn:qftLecture3:460}
S = \int d^d x \lr{ \dotphi^2 – (\spacegrad \phi)^2 }.
\end{equation}
The measure transforms using a Jacobian, which we have seen is the Lorentz transform matrix, and has unit determinant
\begin{equation}\label{eqn:qftLecture3:480}
d^d x’ = d^d x \Abs{ det( \Lambda^{-1} ) } = d^d x.
\end{equation}

Problems.

Question: Four vector form of the Maxwell gauge transformation.

Show that the transformation
\begin{equation}\label{eqn:qftLecture3:580}
A^\mu \rightarrow A^\mu + \partial^\mu \chi
\end{equation}
is the desired four-vector form of the gauge transformation \ref{eqn:qftLecture3:520}, that is
\begin{equation}\label{eqn:qftLecture3:540}
\begin{aligned}
j^\nu
&= \partial_\mu {F’}^{\mu\nu} \\
&= \partial_\mu F^{\mu\nu}.
\end{aligned}
\end{equation}
Also relate this four-vector gauge transformation to the spacetime split.

Answer

\begin{equation}\label{eqn:qftLecture3:560}
\begin{aligned}
\partial_\mu {F’}^{\mu\nu}
&=
\partial_\mu \lr{ \partial^\mu {A’}^\nu – \partial_\nu {A’}^\mu } \\
&=
\partial_\mu \lr{
\partial^\mu \lr{ A^\nu + \partial^\nu \chi }
– \partial_\nu \lr{ A^\mu + \partial^\mu \chi }
} \\
&=
\partial_\mu {F}^{\mu\nu}
+
\partial_\mu \partial^\mu \partial^\nu \chi
–
\partial_\mu \partial^\nu \partial^\mu \chi \\
&=
\partial_\mu {F}^{\mu\nu},
\end{aligned}
\end{equation}
by equality of mixed partials. Expanding \ref{eqn:qftLecture3:580} explicitly we find
\begin{equation}\label{eqn:qftLecture3:600}
{A’}^\mu = A^\mu + \partial^\mu \chi,
\end{equation}
which is
\begin{equation}\label{eqn:qftLecture3:620}
\begin{aligned}
\phi’ = {A’}^0 &= A^0 + \partial^0 \chi = \phi + \dot{\chi} \\
\BA’ \cdot \Be_k = {A’}^k &= A^k + \partial^k \chi = \lr{ \BA – \spacegrad \chi } \cdot \Be_k.
\end{aligned}
\end{equation}
The last of which can be written in vector notation as \( \BA’ = \BA – \spacegrad \chi \).

UofT QFT Fall 2018 Lecture 2. Units, scales, and Lorentz transformations. Taught by Prof. Erich Poppitz

September 17, 2018 phy2403 , , ,

[Click here for a PDF of this post with nicer formatting]

DISCLAIMER: Very rough notes from class. Some additional side notes, but otherwise barely edited.

Natural units.

\begin{equation}\label{eqn:qftLecture2:20}
\begin{aligned}
[\Hbar] &= [\text{action}] = M \frac{L^2}{T^2} T = \frac{M L^2}{T} \\
&= [\text{velocity}] = \frac{L}{T} \\
& [\text{energy}] = M \frac{L^2}{T^2}.
\end{aligned}
\end{equation}

Setting \( c = 1 \) means
\begin{equation}\label{eqn:qftLecture2:240}
\frac{L}{T} = 1
\end{equation}
and setting \( \Hbar = 1 \) means
\begin{equation}\label{eqn:qftLecture2:260}
[\Hbar] = [\text{action}] = M L {\frac{L}{T}} = M L
\end{equation}
therefore
\begin{equation}\label{eqn:qftLecture2:280}
[L] = \inv{\text{mass}}
\end{equation}
and
\begin{equation}\label{eqn:qftLecture2:300}
[\text{energy}] = M {\frac{L^2}{T^2}} = \text{mass}\, \text{eV}
\end{equation}

Summary

  • \( \text{energy} \sim \text{eV} \)
  • \( \text{distance} \sim \inv{M} \)
  • \( \text{time} \sim \inv{M} \)

From:
\begin{equation}\label{eqn:qftLecture2:320}
\alpha = \frac{e^2}{4 \pi {\Hbar c}}
\end{equation}
which is dimensionless (\(1/137\)), so electric charge is dimensionless.

Some useful numbers in natural units

\begin{equation}\label{eqn:qftLecture2:40}
\begin{aligned}
m_\txte &\sim 10^{-27} \text{g} \sim 0.5 \text{MeV} \\
m_\txtp &\sim 2000 m_\txte \sim 1 \text{GeV} \\
m_\pi &\sim 140 \text{MeV} \\
m_\mu &\sim 105 \text{MeV} \\
\Hbar c &\sim 200 \text{MeV} \,\text{fm} = 1
\end{aligned}
\end{equation}

Gravity

Interaction energy of two particles

\begin{equation}\label{eqn:qftLecture2:60}
G_\txtN \frac{m_1 m_2}{r}
\end{equation}

\begin{equation}\label{eqn:qftLecture2:80}
[\text{energy}] \sim [G_\txtN] \frac{M^2}{L}
\end{equation}

\begin{equation}\label{eqn:qftLecture2:100}
[G_\txtN]
\sim
[\text{energy}] \frac{L}{M^2}
\end{equation}

but energy x distance is dimensionless (action) in our units

\begin{equation}\label{eqn:qftLecture2:120}
[G_\txtN]
\sim
{\text{dimensionless}}{M^2}
\end{equation}

\begin{equation}\label{eqn:qftLecture2:140}
\frac{G_\txtN}{\Hbar c} \sim \inv{M^2} \sim \frac{1}{10^{20} \text{GeV}}
\end{equation}

Planck mass

\begin{equation}\label{eqn:qftLecture2:160}
M_{\text{Planck}} \sim \sqrt{\frac{\Hbar c}{G_\txtN}}
\sim 10^{-4} g \sim \inv{\lr{10^{20} \text{GeV}}^2}
\end{equation}

We can revisit the scale diagram from last lecture in terms of MeV mass/energy values, as sketched in fig. 1.

fig. 1. Scales, take II.

At the classical electron radius scale, we consider phenomena such as back reaction of radiation, the self energy of electrons. At the Compton wavelength we have to allow for production of multiple particle pairs. At Bohr radius scales we must start using QM instead of classical mechanics.

Cross section.

Verbal discussion of cross section, not captured in these notes. Roughly, the cross section sounds like the number of events per unit time, related to the flux of some source through an area.

We’ll compute the cross section of a number of different systems in this course. The cross section is relevant in scattering such as the electron-electron scattering sketched in fig. 2.

fig. 2. Electron electron scattering.

We assume that QED is highly relativistic. In natural units, our scale factor is basically the square of the electric charge
\begin{equation}\label{eqn:qftLecture2:180}
\alpha \sim e^2,
\end{equation}
so the cross section has the form
\begin{equation}\label{eqn:qftLecture2:200}
\sigma \sim \frac{\alpha^2}{E^2} \lr{ 1 + O(\alpha) + O(\alpha^2) + \cdots }
\end{equation}

In gravity we could consider scattering of electrons, where \( G_\txtN \) takes the place of \( \alpha \). However, \( G_\txtN \) has dimensions.

For electron-electron scattering due to gravitons

\begin{equation}\label{eqn:qftLecture2:220}
\sigma \sim \frac{G_\txtN^2 E^2}{1 + G_\txtN E^2 + \cdots }
\end{equation}

Now the cross section grows with energy. This will cause some problems (violating unitarity: probabilities greater than 1!) when \( O(G_\txtN E^2) = 1 \).

In any quantum field theories when the coupling constant is not-dimensionless we have the same sort of problems at some scale.

The point is that we can get far considering just dimensional analysis.

If the coupling constant has a dimension \((1/\text{mass})^N\,, N > 0\), then unitarity will be violated at high energy. One such theory is the Fermi theory of beta decay (electro-weak theory), which had a coupling constant with dimensions inverse-mass-squared. The relevant scale for beta decay was 4 Fermi, or \( G_\txtF \sim (1/{100 \text{GeV}})^2 \). This was the motivation for introducing the Higgs theory, which was motivated by restoring unitarity.

Lorentz transformations.

The goal, perhaps not for today, is to study the simplest (relativistic) scalar field theory. First studied classically, and then consider such a quantum field theory.

How is relativity implemented when we write the Lagrangian and action?

Our first step must be to consider Lorentz transformations and the Lorentz group.

Spacetime (Minkowski space) is \R{3,1} (or \R{d-1,1}). Our coordinates are

\begin{equation}\label{eqn:qftLecture2:340}
(c t, x^1, x^2, x^3) = (c t, \Br).
\end{equation}

Here, we’ve scaled the time scale by \( c \) so that we measure time and space in the same dimensions. We write this as

\begin{equation}\label{eqn:qftLecture2:360}
x^\mu = (x^0, x^1, x^2, x^3),
\end{equation}

where \( \mu = 0, 1, 2, 3 \), and call this a “4-vector”. These are called the space-time coordinates of an event, which tell us where and when an event occurs.

For two events whose spacetime coordinates differ by \( dx^0, dx^1, dx^2, dx^3 \) we introduce the notion of a space time \underline{interval}

\begin{equation}\label{eqn:qftLecture2:380}
\begin{aligned}
ds^2
&= c^2 dt^2
– (dx^1)^2
– (dx^2)^2
– (dx^3)^2 \\
&=
\sum_{\mu, \nu = 0}^3 g_{\mu\nu} dx^\mu dx^\nu
\end{aligned}
\end{equation}

Here \( g_{\mu\nu} \) is the Minkowski space metric, an object with two indexes that run from 0-3. i.e. this is a diagonal matrix

\begin{equation}\label{eqn:qftLecture2:400}
g_{\mu\nu} \sim
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & -1 \\
\end{bmatrix}
\end{equation}

i.e.
\begin{equation}\label{eqn:qftLecture2:420}
\begin{aligned}
g_{00} &= 1 \\
g_{11} &= -1 \\
g_{22} &= -1 \\
g_{33} &= -1 \\
\end{aligned}
\end{equation}

We will use the Einstein summation convention, where any repeated upper and lower indexes are considered summed over. That is \ref{eqn:qftLecture2:380} is written with an implied sum
\begin{equation}\label{eqn:qftLecture2:440}
ds^2 = g_{\mu\nu} dx^\mu dx^\nu.
\end{equation}

Explicit expansion:
\begin{equation}\label{eqn:qftLecture2:460}
\begin{aligned}
ds^2
&= g_{\mu\nu} dx^\mu dx^\nu \\
&=
g_{00} dx^0 dx^0
+g_{11} dx^1 dx^1
+g_{22} dx^2 dx^2
+g_{33} dx^3 dx^3
&=
(1) dx^0 dx^0
+ (-1) dx^1 dx^1
+ (-1) dx^2 dx^2
+ (-1) dx^3 dx^3.
\end{aligned}
\end{equation}

Recall that rotations (with orthogonal matrix representations) are transformations that leave the dot product unchanged, that is

\begin{equation}\label{eqn:qftLecture2:480}
\begin{aligned}
(R \Bx) \cdot (R \By)
&= \Bx^\T R^\T R \By \\
&= \Bx^\T \By \\
&= \Bx \cdot \By,
\end{aligned}
\end{equation}

where \( R \) is a rotation orthogonal 3×3 matrix. The set of such transformations that leave the dot product unchanged have orthonormal matrix representations \( R^\T R = 1 \). We call the set of such transformations that have unit determinant the SO(3) group.

We call a Lorentz transformation, if it is a linear transformation acting on 4 vectors that leaves the spacetime interval (i.e. the inner product of 4 vectors) invariant. That is, a transformation that leaves
\begin{equation}\label{eqn:qftLecture2:500}
x^\mu y^\nu g_{\mu\nu} = x^0 y^0 – x^1 y^1 – x^2 y^2 – x^3 y^3
\end{equation}
unchanged.

Suppose that transformation has a 4×4 matrix form

\begin{equation}\label{eqn:qftLecture2:520}
{x’}^\mu = {\Lambda^\mu}_\nu x^\nu
\end{equation}

For an example of a possible \( \Lambda \), consider the transformation sketched in fig. 3.

fig. 3. Boost transformation.

We know that boost has the form
\begin{equation}\label{eqn:qftLecture2:540}
\begin{aligned}
x &= \frac{x’ + v t’}{\sqrt{1 – v^2/c^2}} \\
y &= y’ \\
z &= z’ \\
t &= \frac{t’ + (v/c^2) x’}{\sqrt{1 – v^2/c^2}} \\
\end{aligned}
\end{equation}
(this is a boost along the x-axis, not y as I’d drawn),
or
\begin{equation}\label{eqn:qftLecture2:560}
\begin{bmatrix}
c t \\
x \\
y \\
z
\end{bmatrix}
=
\begin{bmatrix}
\inv{\sqrt{1 – v^2/c^2}} & \frac{v/c}{\sqrt{1 – v^2/c^2}} & 0 & 0 \\
\frac{v/c}{\sqrt{1 – v^2/c^2}} & \frac{1}{\sqrt{1 – v^2/c^2}} & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
c t’ \\
x’ \\
y’ \\
z’
\end{bmatrix}
\end{equation}

Other examples include rotations (\({\lambda^0}_0 = 1\) zeros in \( {\lambda^0}_k, {\lambda^k}_0 \), and a rotation matrix in the remainder.)

Back to Lorentz transformations (\(\text{SO}(1,3)^+\)), let
\begin{equation}\label{eqn:qftLecture2:600}
\begin{aligned}
{x’}^\mu &= {\Lambda^\mu}_\nu x^\nu \\
{y’}^\kappa &= {\Lambda^\kappa}_\rho y^\rho
\end{aligned}
\end{equation}

The dot product
\begin{equation}\label{eqn:qftLecture2:620}
g_{\mu \kappa}
{x’}^\mu
{y’}^\kappa
=
g_{\mu \kappa}
{\Lambda^\mu}_\nu
{\Lambda^\kappa}_\rho
x^\nu
y^\rho
=
g_{\nu\rho}
x^\nu
y^\rho,
\end{equation}
where the last step introduces the invariance requirement of the transformation. That is

\begin{equation}\label{eqn:qftLecture2:640}
\boxed{
g_{\nu\rho}
=
g_{\mu \kappa}
{\Lambda^\mu}_\nu
{\Lambda^\kappa}_\rho.
}
\end{equation}

Upper and lower indexes

We’ve defined

\begin{equation}\label{eqn:qftLecture2:660}
x^\mu = (t, x^1, x^2, x^3)
\end{equation}

We could also define a four vector with lower indexes
\begin{equation}\label{eqn:qftLecture2:680}
x_\nu = g_{\nu\mu} x^\mu = (t, -x^1, -x^2, -x^3).
\end{equation}
That is
\begin{equation}\label{eqn:qftLecture2:700}
\begin{aligned}
x_0 &= x^0 \\
x_1 &= -x^1 \\
x_2 &= -x^2 \\
x_3 &= -x^3.
\end{aligned}
\end{equation}

which allows us to write the dot product as simply \( x^\mu y_\mu \).

We can also define a metric tensor with upper indexes

\begin{equation}\label{eqn:qftLecture2:401}
g^{\mu\nu} \sim
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & -1 \\
\end{bmatrix}
\end{equation}
This is the inverse matrix of \( g_{\mu\nu} \), and it satisfies
\begin{equation}\label{eqn:qftLecture2:720}
g^{\mu \nu} g_{\nu\rho} = {\delta^\mu}_\rho
\end{equation}

Exercise: Check:
\begin{equation}\label{eqn:qftLecture2:740}
\begin{aligned}
g_{\mu\nu} x^\mu y^\nu
&= x_\nu y^\nu \\
&= x^\nu y_\nu \\
&= g^{\mu\nu} x_\mu y_\nu \\
&= {\delta^\mu}_\nu x_\mu y^\nu.
\end{aligned}
\end{equation}

Class ended around this point, but it appeared that we were heading this direction:

Returning to the Lorentz invariant and multiplying both sides of
\ref{eqn:qftLecture2:640} with an inverse Lorentz transformation \( \Lambda^{-1} \), we find
\begin{equation}\label{eqn:qftLecture2:760}
\begin{aligned}
g_{\nu\rho}
{\lr{\Lambda^{-1}}^\rho}_\alpha
&=
g_{\mu \kappa}
{\Lambda^\mu}_\nu
{\Lambda^\kappa}_\rho
{\lr{\Lambda^{-1}}^\rho}_\alpha \\
&=
g_{\mu \kappa}
{\Lambda^\mu}_\nu
{\delta^\kappa}_\alpha \\
&=
g_{\mu \alpha}
{\Lambda^\mu}_\nu,
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:qftLecture2:780}
\lr{\Lambda^{-1}}_{\nu \alpha} = \Lambda_{\alpha \nu}.
\end{equation}
This is clearly analogous to \( R^\T = R^{-1} \), although the index notation obscures things considerably. Prof. Poppitz said that next week this would all lead to showing that the determinant of any Lorentz transformation was \( \pm 1 \).

For what it’s worth, it seems to me that this index notation makes life a lot harder than it needs to be, at least for a matrix related question (i.e. determinant of the transformation). In matrix/column-(4)-vector notation, let \(x’ = \Lambda x, y’ = \Lambda y\) be two four vector transformations, then
\begin{equation}\label{eqn:qftLecture2:800}
x’ \cdot y’ = {x’}^T G y’ = (\Lambda x)^T G \Lambda y = x^T ( \Lambda^T G \Lambda) y = x^T G y.
\end{equation}
so
\begin{equation}\label{eqn:qftLecture2:820}
\boxed{
\Lambda^T G \Lambda = G.
}
\end{equation}
Taking determinants of both sides gives \(-(det(\Lambda))^2 = -1\), and thus \(det(\Lambda) = \pm 1\).

UofT QFT Fall 2018 phy2403 ; Lecture 1, What is a field? Taught by Prof. Erich Poppitz

September 14, 2018 math and physics play

[Click here for a PDF of this post with nicer formatting]

DISCLAIMER: Very rough notes from class. Some additional side notes, but otherwise barely edited.

What is a field?

A field is a map from space(time) to some set of numbers. These set of numbers may be organized some how, possibly scalars, or vectors, …

One example is the familiar spacetime vector, where \( \Bx \in \mathbb{R}^{d} \)

\begin{equation}\label{eqn:qftLecture1:20}
(\Bx, t) \rightarrow \mathbb{R}^{\lr{d,1}}
\end{equation}

Examples of fields:

  1. \( 0 + 1 \) dimensional “QFT”, where the spatial dimension is zero dimensional and we have one time dimension. Fields in this case are just functions of time \( x(t) \). That is, particle mechanics is a 0 + 1 dimensional classical field theory. We know that classical mechanics is described by the action
    \begin{equation}\label{eqn:qftLecture1:40}
    S = \frac{m}{2} \int dt \xdot^2.
    \end{equation}
    This is non-relativistic. We can make this relativistic by saying this is the first order term in the Taylor expansion
    \begin{equation}\label{eqn:qftLecture1:60}
    S = – m c^2 \int dt \sqrt{ 1 – \xdot^2/c^2 }.
    \end{equation}
    Classical field theory (of \( x(t) \)). The “QFT” of \( x(t) \). i.e. QM.
    All of you know quantum mechanics. If you don’t just leave. Not this way (pointing to the window), but this way (pointing to the door).
    The solution of a quantum mechanical state is
    \begin{equation}\label{eqn:qftLecture1:80}
    \bra{x} e^{-i H t/\,\hbar } \ket{x’},
    \end{equation}
    which can be found by evaluating the “Feynman path integral”
    \begin{equation}\label{eqn:qftLecture1:100}
    \sum_{\text{all paths x}} e^{i S[x]/\,\hbar}
    \end{equation}
    This will be particularly useful for QFT, despite the fact that such a sum is really hard to evaluate (try it for the Hydrogen atom for example).
  2. \( 3 + 0 \) dimensional field theory, where we have 3 spatial dimensions and 0 time dimensions. Classical equilibrium static systems. The field may have a structure like
    \begin{equation}\label{eqn:qftLecture1:120}
    \Bx \rightarrow \BM(\Bx),
    \end{equation}
    for example, magnetization.
    We can write the solution to such a system using the partition function
    \begin{equation}\label{eqn:qftLecture1:140}
    Z \sim \sum_{\text{all} \BM(x)} e^{-E[\BM]/\kB T}.
    \end{equation}
    For such a system the energy function may be like
    \begin{equation}\label{eqn:qftLecture1:160}
    E[\BM] = \int d^3 \Bx \lr{ a \BM^2(\Bx) + b \BM^4(\Bx) + c \sum_{i = 1}^3 \lr{ \PD{x_i}{} \BM }
    \cdot \lr{ \PD{x_i}{} \BM }
    }.
    \end{equation}
    There is an analogy between the partition function and the Feynman path integral, as both are summing over all possible energy states in both cases.
    This will be probably be the last time that we mention the partition function and condensed matter physics in this term for this class.
  3. \( 3 + 1 \) dimensional field theories, with 3 spatial dimensions and 1 time dimension.
    Example, electromagnetism with \( \BE(\Bx, t), \BB(\Bx, t) \) or better use \( \BA(\Bx, t), \phi(\Bx, t) \). The action is
    \begin{equation}\label{eqn:qftLecture1:180}
    S = -\inv{16 \pi c} \int d^3 \Bx dt \lr{ \BE^2 – \BB^2 }.
    \end{equation}
    This is our first example of a relativistic field theory in \( 3 + 1 \) dimensions. It will take us a while to get there.

These are examples of classical field theories, such as fluid dynamics and general relativity. We want to consider electromagnetism because this is the place that we everything starts to fall apart (i.e. blackbody radiation, relating to the equilibrium states of radiating matter). Part of the resolution of this was the quantization of the energy states, where we studied the normal modes of electromagnetic radiation in a box. These modes can be considered an infinite number of radiating oscillators (the ultraviolet catastrophe). This was resolved by Planck by requiring those energy states to be quantized (an excellent discussion of this can be found in [1]. In that sense you have already seen quantum field theory.

For electromagnetism the classical description is not always good. Examples:

  1. blackbody radiation.
  2. electron energy \( e^2/r_\txte \) of a point charge diverges as \( r_\txte \rightarrow 0 \).
    We can define the classical radius of the electron by
    \begin{equation}\label{eqn:qftLecture1:200}
    \frac{e^2}{r^{\textrm{cl}}_{\txte}} \sim m_\txte c^2,
    \end{equation}
    or
    \begin{equation}\label{eqn:qftLecture1:220}
    r^{\textrm{cl}}_{\txte} \sim \frac{m_\txte c^2}{e^2} \sim 10^{-15} \text{m}
    \end{equation}
    Don’t treat this very seriously, but it becomes useful at frequencies \( \omega \sim c/r_\txte \), where \( r_\txte/c \) is approximately the time for light to cross a distance \( r_\txte \).
    At frequencies like this, we should not believe the solutions that are obtained by classical electrodynamics.
    In particular, self-accelerating solutions appear at these frequencies in classical EM. This is approximately \( \omega_\conj \sim 10^{23} Hz \), or
    \begin{equation}\label{eqn:qftLecture1:240}
    \begin{aligned}
    \,\hbar \omega_\conj
    &\sim \lr{ 10^{-21} \,\text{MeV s}} \lr{ 10^{23} \,\text{1/s} }\\
    &\sim 100 \text{MeV}.
    \end{aligned}
    \end{equation}

At such frequencies particle creation becomes possible.

Scales

A (dimensionless) value that is very useful in determining scale is
\begin{equation}\label{eqn:qftLecture1:260}
\alpha = \frac{e^2}{4 \pi \,\hbar c} \sim \inv{137},
\end{equation}
called the fine scale constant, which relates three important scales relevant to quantum mechanics, as sketched in fig. 1.

fig. 1. Interesting scales in quantum mechanics.

fig. 1. Interesting scales in quantum mechanics.

 

  • The Bohr radius (large end of the scale).
  • The Compton wavelength of the electron.
  • The classical radius of the electron.

Bohr radius

A quick motivation for the Bohr radius was mentioned in passing in class while discussing scale, following the high school method of deriving the Balmer series ([2]).

That method assumes a circular electron trajectory (\(i = \Be_1 \Be_2\))
\begin{equation}\label{eqn:qftLecture1:280}
\begin{aligned}
\Br &= r \Be_1 e^{i \omega t} \\
\Bv &= \omega r \Be_2 e^{i \omega t} \\
\Ba &= -\omega^2 r \Be_1 e^{i \omega t} \\
\end{aligned}
\end{equation}
The Coulomb force (in cgs units) on the electron is
\begin{equation}\label{eqn:qftLecture1:300}
\BF = m\Ba = -m \omega^2 r \Be_1 e^{i \omega t} = \frac{-e (e)}{r^2} \Be_1 e^{i \omega t},
\end{equation}
or
\begin{equation}\label{eqn:qftLecture1:320}
m \lr{ \frac{v}{r}}^2 r = \frac{e^2}{r^2},
\end{equation}
giving
\begin{equation}\label{eqn:qftLecture1:340}
m v^2 = \frac{e^2}{r}.
\end{equation}
The energy of the system, including both Kinetic and potential (from an infinite reference point) is
\begin{equation}\label{eqn:qftLecture1:360}
\begin{aligned}
E
&= \inv{2} m v^2 – \frac{e^2}{r} \\
&= – \inv{2} m v^2 \sim \,\hbar \omega = \,\hbar \frac{v}{r},
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:qftLecture1:380}
m v r \sim \,\hbar.
\end{equation}
Eliminating \( v \) using \ref{eqn:qftLecture1:340}, assuming a ground state radius \( r = a_0 \) gives

\begin{equation}\label{eqn:qftLecture1:400}
a_0 \sim \frac{\hbar^2}{m e^2}.
\end{equation}
The Bohr radius is of the order \( 10^{-10} \text{m} \).

Compton wavelength.

When particle momentum starts approaching the speed of light, by the uncertainty relation (\(\Delta x \Delta p \sim \,\hbar\)) the variation in position must be of the order
\begin{equation}\label{eqn:qftLecture1:420}
\lambda_\txtc \sim \frac{\hbar}{m_\txte c},
\end{equation}
called the Compton wavelength.
Similarly, when the length scales are reduced to the Compton wavelength, the momentum increases to relativistic levels.
Because of the relativistic velocities at the Compton wavelength, particle creation and annihilation occurs and any theory has to account for multiple particle states.

Relations.

Scaling the Bohr radius once by the fine structure constant, we obtain the Compton wavelength (after dropping factors of \( 4\pi \))
\begin{equation}\label{eqn:qftLecture1:440}
\begin{aligned}
a_0 \alpha
&= \frac{\hbar^2}{m e^2}
\frac{e^2}{4 \pi \,\hbar c} \\
&= \frac{\hbar}{4 \pi m c} \\
&\sim
\frac{\hbar}{m c} \\
&= \lambda_\txtc.
\end{aligned}
\end{equation}
Scaling once more, we obtain (after dropping another \( 4\pi\)) the classical electron radius
\begin{equation}\label{eqn:qftLecture1:n}
\begin{aligned}
\lambda_\txtc \alpha
&=
\frac{e^2}{4 \pi m c^2} \\
&\sim
\frac{e^2}{m c^2}.
\end{aligned}
\end{equation}

References

[1] D. Bohm. Quantum Theory. Courier Dover Publications, 1989.

[2] A.P. French and E.F. Taylor. An Introduction to Quantum Physics. CRC Press, 1998.

Applied vanity press

April 9, 2018 math and physics play , , , ,

Amazon’s createspace turns out to be a very cost effective way to get a personal color copy of large pdf (>250 pages) to markup for review. The only hassle was having to use their app to create cover art (although that took less time than commuting downtown to one of the cheap copy shops near the university.)

As a side effect, after I edit it, I’d have something I could actually list for sale.  Worldwide, I’d guess at least three people would buy it, that is, if they weren’t happy with the pdf version already available.