angular momentum

Totally asymmetric potential

December 16, 2015 phy1520 , , ,

[Click here for a PDF of this post with nicer formatting]

Q: [1] pr 4.11

(a) Given a time reversal invariant Hamiltonian, show that for any energy eigenket

\begin{equation}\label{eqn:totallyAsymmetricPotential:20}
\expectation{\BL} = 0.
\end{equation}

(b) If the wave function of such a state is expanded as

\begin{equation}\label{eqn:totallyAsymmetricPotential:40}
\sum_{l,m} F_{l m} Y_{l m}(\theta, \phi),
\end{equation}

what are the phase restrictions on \( F_{lm} \)?

A: part (a)

For a time reversal invariant Hamiltonian \( H \) we have

\begin{equation}\label{eqn:totallyAsymmetricPotential:60}
H \Theta = \Theta H.
\end{equation}

If \( \ket{\psi} \) is an energy eigenstate with eigenvalue \( E \), we have

\begin{equation}\label{eqn:totallyAsymmetricPotential:80}
\begin{aligned}
H \Theta \ket{\psi}
&= \Theta H \ket{\psi} \\
&= \lambda \Theta \ket{\psi},
\end{aligned}
\end{equation}

so \( \Theta \ket{\psi} \) is also an eigenvalue of \( H \), so can only differ from \( \ket{\psi} \) by a phase factor. That is

\begin{equation}\label{eqn:totallyAsymmetricPotential:100}
\begin{aligned}
\ket{\psi’}
&=
\Theta \ket{\psi} \\
&= e^{i\delta} \ket{\psi}.
\end{aligned}
\end{equation}

Now consider the expectation of \( \BL \) with respect to a time reversed state

\begin{equation}\label{eqn:totallyAsymmetricPotential:120}
\begin{aligned}
\bra{ \psi’} \BL \ket{\psi’}
&=
\bra{ \psi} \Theta^{-1} \BL \Theta \ket{\psi} \\
&=
\bra{ \psi} (-\BL) \ket{\psi},
\end{aligned}
\end{equation}

however, we also have

\begin{equation}\label{eqn:totallyAsymmetricPotential:140}
\begin{aligned}
\bra{ \psi’} \BL \ket{\psi’}
&=
\lr{ \bra{ \psi} e^{-i\delta} } \BL \lr{ e^{i\delta} \ket{\psi} } \\
&=
\bra{\psi} \BL \ket{\psi},
\end{aligned}
\end{equation}

so we have \( \bra{\psi} \BL \ket{\psi} = -\bra{\psi} \BL \ket{\psi} \) which is only possible if \( \expectation{\BL} = \bra{\psi} \BL \ket{\psi} = 0\).

A: part (b)

Consider the expansion of the wave function of a time reversed energy eigenstate

\begin{equation}\label{eqn:totallyAsymmetricPotential:160}
\begin{aligned}
\bra{\Bx} \Theta \ket{\psi}
&=
\bra{\Bx} e^{i\delta} \ket{\psi} \\
&=
e^{i\delta} \braket{\Bx}{\psi},
\end{aligned}
\end{equation}

and then consider the same state expanded in the position basis

\begin{equation}\label{eqn:totallyAsymmetricPotential:180}
\begin{aligned}
\bra{\Bx} \Theta \ket{\psi}
&=
\bra{\Bx} \Theta \int d^3 \Bx’ \lr{ \ket{\Bx’}\bra{\Bx’} } \ket{\psi} \\
&=
\bra{\Bx} \Theta \int d^3 \Bx’ \lr{ \braket{\Bx’}{\psi} } \ket{\Bx’} \\
&=
\bra{\Bx} \int d^3 \Bx’ \lr{ \braket{\Bx’}{\psi} }^\conj \Theta \ket{\Bx’} \\
&=
\bra{\Bx} \int d^3 \Bx’ \lr{ \braket{\Bx’}{\psi} }^\conj \ket{\Bx’} \\
&=
\int d^3 \Bx’ \lr{ \braket{\Bx’}{\psi} }^\conj \braket{\Bx}{\Bx’} \\
&=
\int d^3 \Bx’ \braket{\psi}{\Bx’} \delta(\Bx- \Bx’) \\
&=
\braket{\psi}{\Bx}.
\end{aligned}
\end{equation}

This demonstrates a relationship between the wave function and its complex conjugate

\begin{equation}\label{eqn:totallyAsymmetricPotential:200}
\braket{\Bx}{\psi} = e^{-i\delta} \braket{\psi}{\Bx}.
\end{equation}

Now expand the wave function in the spherical harmonic basis

\begin{equation}\label{eqn:totallyAsymmetricPotential:220}
\begin{aligned}
\braket{\Bx}{\psi}
&=
\int d\Omega \braket{\Bx}{\ncap}\braket{\ncap}{\psi} \\
&=
\sum_{lm} F_{lm}(r) Y_{lm}(\theta, \phi) \\
&=
e^{-i\delta}
\lr{
\sum_{lm} F_{lm}(r) Y_{lm}(\theta, \phi) }^\conj \\
&=
e^{-i\delta}
\sum_{lm} \lr{ F_{lm}(r)}^\conj Y_{lm}^\conj(\theta, \phi) \\
&=
e^{-i\delta}
\sum_{lm} \lr{ F_{lm}(r)}^\conj (-1)^m Y_{l,-m}(\theta, \phi) \\
&=
e^{-i\delta}
\sum_{lm} \lr{ F_{l,-m}(r)}^\conj (-1)^m Y_{l,m}(\theta, \phi),
\end{aligned}
\end{equation}

so the \( F_{lm} \) functions are constrained by

\begin{equation}\label{eqn:totallyAsymmetricPotential:240}
F_{lm}(r) = e^{-i\delta} \lr{ F_{l,-m}(r)}^\conj (-1)^m.
\end{equation}

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

Angular momentum expectation values

December 14, 2015 phy1520 ,

[Click here for a PDF of this post with nicer formatting]

Q: [1] pr 3.18

Compute the expectation values for the first and second powers of the angular momentum operators with respect to states \( \ket{lm} \).

A:

We can write the expectation values for the \( L_z \) powers immediately

\begin{equation}\label{eqn:angularMomentumExpectation:20}
\expectation{L_z}
= m \Hbar,
\end{equation}

and

\begin{equation}\label{eqn:angularMomentumExpectation:40}
\expectation{L_z^2} = (m \Hbar)^2.
\end{equation}

For the x and y components first express the operators in terms of the ladder operators.

\begin{equation}\label{eqn:angularMomentumExpectation:60}
\begin{aligned}
L_{+} &= L_x + i L_y \\
L_{-} &= L_x – i L_y.
\end{aligned}
\end{equation}

Rearranging gives

\begin{equation}\label{eqn:angularMomentumExpectation:80}
\begin{aligned}
L_x &= \inv{2} \lr{ L_{+} + L_{-} } \\
L_y &= \inv{2i} \lr{ L_{+} – L_{-} }.
\end{aligned}
\end{equation}

The first order expectations \( \expectation{L_x}, \expectation{L_y} \) are both zero since \( \expectation{L_{+}} = \expectation{L_{-}} \). For the second order expectation values we have

\begin{equation}\label{eqn:angularMomentumExpectation:100}
\begin{aligned}
L_x^2
&= \inv{4} \lr{ L_{+} + L_{-} } \lr{ L_{+} + L_{-} } \\
&= \inv{4} \lr{ L_{+} L_{+} + L_{-} L_{-} + L_{+} L_{-} + L_{-} L_{+} } \\
&= \inv{4} \lr{ L_{+} L_{+} + L_{-} L_{-} + 2 (L_x^2 + L_y^2) } \\
&= \inv{4} \lr{ L_{+} L_{+} + L_{-} L_{-} + 2 (\BL^2 – L_z^2) },
\end{aligned}
\end{equation}

and
\begin{equation}\label{eqn:angularMomentumExpectation:120}
\begin{aligned}
L_y^2
&= -\inv{4} \lr{ L_{+} – L_{-} } \lr{ L_{+} – L_{-} } \\
&= -\inv{4} \lr{ L_{+} L_{+} + L_{-} L_{-} – L_{+} L_{-} – L_{-} L_{+} } \\
&= -\inv{4} \lr{ L_{+} L_{+} + L_{-} L_{-} – 2 (L_x^2 + L_y^2) } \\
&= -\inv{4} \lr{ L_{+} L_{+} + L_{-} L_{-} – 2 (\BL^2 – L_z^2) }.
\end{aligned}
\end{equation}

Any expectation value \( \bra{lm} L_{+} L_{+} \ket{lm} \) or \( \bra{lm} L_{-} L_{-} \ket{lm} \) will be zero, leaving

\begin{equation}\label{eqn:angularMomentumExpectation:140}
\begin{aligned}
\expectation{L_x^2}
&=
\expectation{L_y^2} \\
&=
\inv{4} \expectation{2 (\BL^2 – L_z^2) } \\
&=
\inv{2} \lr{ \Hbar^2 l(l+1) – (\Hbar m)^2 }.
\end{aligned}
\end{equation}

Observe that we have
\begin{equation}\label{eqn:angularMomentumExpectation:160}
\expectation{L_x^2}
+
\expectation{L_y^2}
+
\expectation{L_z^2}
=
\Hbar^2 l(l+1)
=
\expectation{\BL^2},
\end{equation}

which is the quantum mechanical analogue of the classical scalar equation \( \BL^2 = L_x^2 + L_y^2 + L_z^2 \).

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

L_z and L^2 eigenvalues and probabilities for a given wave function

December 13, 2015 phy1520 , , , , ,

[Click here for a PDF of this post with nicer formatting]

Q: [1] 3.17

Given a wave function

\begin{equation}\label{eqn:LsquaredLzProblem:20}
\psi(r,\theta, \phi) = f(r) \lr{ x + y + 3 z },
\end{equation}

  • (a) Determine if this wave function is an eigenfunction of \( \BL^2 \), and the value of \( l \) if it is an eigenfunction.

  • (b) Determine the probabilities for the particle to be found in any given \( \ket{l, m} \) state,
  • (c) If it is known that \( \psi \) is an energy eigenfunction with energy \( E \) indicate how we can find \( V(r) \).

A: (a)

Using
\begin{equation}\label{eqn:LsquaredLzProblem:40}
\BL^2
=
-\Hbar^2 \lr{ \inv{\sin^2\theta} \partial_{\phi\phi} + \inv{\sin\theta} \partial_\theta \lr{ \sin\theta \partial_\theta} },
\end{equation}

and

\begin{equation}\label{eqn:LsquaredLzProblem:60}
\begin{aligned}
x &= r \sin\theta \cos\phi \\
y &= r \sin\theta \sin\phi \\
z &= r \cos\theta
\end{aligned}
\end{equation}

it’s a quick computation to show that

\begin{equation}\label{eqn:LsquaredLzProblem:80}
\BL^2 \psi = 2 \Hbar^2 \psi = 1(1 + 1) \Hbar^2 \psi,
\end{equation}

so this function is an eigenket of \( \BL^2 \) with an eigenvalue of \( 2 \Hbar^2 \), which corresponds to \( l = 1 \), a p-orbital state.

(b)

Recall that the angular representation of \( L_z \) is

\begin{equation}\label{eqn:LsquaredLzProblem:100}
L_z = -i \Hbar \PD{\phi},
\end{equation}

so we have

\begin{equation}\label{eqn:LsquaredLzProblem:120}
\begin{aligned}
L_z x &= i \Hbar y \\
L_z y &= – i \Hbar x \\
L_z z &= 0,
\end{aligned}
\end{equation}

The \( L_z \) action on \( \psi \) is

\begin{equation}\label{eqn:LsquaredLzProblem:140}
L_z \psi = -i \Hbar r f(r) \lr{ – y + x }.
\end{equation}

This wave function is not an eigenket of \( L_z \). Expressed in terms of the \( L_z \) basis states \( e^{i m \phi} \), this wave function is

\begin{equation}\label{eqn:LsquaredLzProblem:160}
\begin{aligned}
\psi
&= r f(r) \lr{ \sin\theta \lr{ \cos\phi + \sin\phi} + \cos\theta } \\
&= r f(r) \lr{ \frac{\sin\theta}{2} \lr{ e^{i \phi} \lr{ 1 + \inv{i}} + e^{-i\phi} \lr{ 1 – \inv{i} } } + \cos\theta } \\
&= r f(r) \lr{
\frac{(1-i)\sin\theta}{2} e^{1 i \phi}
+
\frac{(1+i)\sin\theta}{2} e^{- 1 i \phi}
+ \cos\theta e^{0 i \phi}
}
\end{aligned}
\end{equation}

Assuming that \( \psi \) is normalized, the probabilities for measuring \( m = 1,-1,0 \) respectively are

\begin{equation}\label{eqn:LsquaredLzProblem:180}
\begin{aligned}
P_{\pm 1}
&= 2 \pi \rho \Abs{\frac{1\mp i}{2}}^2 \int_0^\pi \sin\theta d\theta \sin^2 \theta \\
&= -2 \pi \rho \int_1^{-1} du (1-u^2) \\
&= 2 \pi \rho \evalrange{ \lr{ u – \frac{u^3}{3} } }{-1}{1} \\
&= 2 \pi \rho \lr{ 2 – \frac{2}{3}} \\
&= \frac{ 8 \pi \rho}{3},
\end{aligned}
\end{equation}

and

\begin{equation}\label{eqn:LsquaredLzProblem:200}
P_{0} = 2 \pi \rho \int_0^\pi \sin\theta \cos\theta = 0,
\end{equation}

where

\begin{equation}\label{eqn:LsquaredLzProblem:220}
\rho = \int_0^\infty r^4 \Abs{f(r)}^2 dr.
\end{equation}

Because the probabilities must sum to 1, this means the \( m = \pm 1 \) states are equiprobable with \( P_{\pm} = 1/2 \), fixing \( \rho = 3/16\pi \), even without knowing \( f(r) \).

(c)

The operator \( r^2 \Bp^2 \) can be decomposed into a \( \BL^2 \) component and some other portions, from which we can write

\begin{equation}\label{eqn:LsquaredLzProblem:240}
\begin{aligned}
H \psi
&= \lr{ \frac{\Bp^2}{2m} + V(r) } \psi \\
&=
\lr{
– \frac{\Hbar^2}{2m} \lr{ \partial_{rr} + \frac{2}{r} \partial_r – \inv{\Hbar^2 r^2} \BL^2 } + V(r) } \psi.
\end{aligned}
\end{equation}

(See: [1] eq. 6.21)

In this case where \( \BL^2 \psi = 2 \Hbar^2 \psi \) we can rearrange for \( V(r) \)

\begin{equation}\label{eqn:LsquaredLzProblem:260}
\begin{aligned}
V(r)
&= E + \inv{\psi} \frac{\Hbar^2}{2m} \lr{ \partial_{rr} + \frac{2}{r} \partial_r – \frac{2}{r^2} } \psi \\
&= E + \inv{f(r)} \frac{\Hbar^2}{2m} \lr{ \partial_{rr} + \frac{2}{r} \partial_r – \frac{2}{r^2} } f(r).
\end{aligned}
\end{equation}

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

PHY1520H Graduate Quantum Mechanics. Lecture 15: angular momentum rotation representation, and angular momentum addition. Taught by Prof. Arun Paramekanti

November 12, 2015 phy1520 , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course PHY1520, Graduate Quantum Mechanics, taught by Prof. Paramekanti, covering chap 3. content from [1].

Angular momentum (wrap up.)

We found

\begin{equation}\label{eqn:qmLecture15:20}
\begin{aligned}
\hat{\BL^2} \ket{j, m} &= j(j+1) \Hbar^2 \ket{j,m} \\
\hat{L}_z \ket{j, m} &= \Hbar m \ket{j,m} \\
\hat{L}_{\pm} \ket{j, m } &= \Hbar \sqrt{(j \mp m)(j \pm m + 1)} \ket{j, m \pm 1 }
\end{aligned}
\end{equation}

or Schwinger

\begin{equation}\label{eqn:qmLecture15:40}
\begin{aligned}
\hat{L}_z &= \inv{2} \lr{ \hat{n}_1 – \hat{n}_2 } \Hbar \\
\hat{L}_{+} &= a_1^\dagger a_2 \Hbar \\
\hat{L}_{-} &= a_1 a_2^\dagger \Hbar \\
j &= \inv{2} \lr{ \hat{n}_1 + \hat{n}_2 },
\end{aligned}
\end{equation}

where each of the \( a_1, a_2 \) operators obey

\begin{equation}\label{eqn:qmLecture15:60}
\begin{aligned}
\antisymmetric{a_1}{a_1^\dagger} &= 1 \\
\antisymmetric{a_2}{a_2^\dagger} &= 1
\end{aligned}
\end{equation}

and any pair of different index \( a \) operators commute, as in

\begin{equation}\label{eqn:qmLecture15:80}
\antisymmetric{a_1}{a_2^\dagger} = 0.
\end{equation}

Representations

It’s possible to compute matrix representations of the rotation operators

\begin{equation}\label{eqn:qmLecture15:100}
\hat{R}_\ncap(\phi) = e^{i \hat{\BL} \cdot \ncap \phi/\Hbar}.
\end{equation}

With respect to a ket it’s possible to find

\begin{equation}\label{eqn:qmLecture15:120}
e^{i \hat{\BL} \cdot \ncap \phi/\Hbar} \ket{j, m}
=
\sum_{m’} d^j_{m m’}(\ncap, \phi) \ket{ j, m’ }.
\end{equation}

This has a block diagonal form that’s sketched in fig. 1.

fig. 1. Block diagonal form for angular momentum matrix representation.

fig. 1. Block diagonal form for angular momentum matrix representation.

We can view \( d^j_{m m’}(\ncap, \phi) \) as a matrix, representing the rotation. The problem of determining these matrices can be reduced to that of determining the matrix for \( \hat{\BL} \), because once we have that we can exponentiate that.

Example: spin 1/2

From the eigenvalue relationships, with basis states

\begin{equation}\label{eqn:qmLecture15:160}
\begin{aligned}
\ket{\uparrow} &=
\begin{bmatrix}
1 \\
0
\end{bmatrix} \\
\ket{\downarrow} &=
\begin{bmatrix}
0 \\
1 \\
\end{bmatrix}
\end{aligned}
\end{equation}

we find

\begin{equation}\label{eqn:qmLecture15:180}
\begin{aligned}
\hat{L}_z &= \frac{\Hbar}{2} \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} \\
\hat{L}_{+} &= \frac{\Hbar}{2}
\begin{bmatrix}
0 & 1 \\
0 & 0
\end{bmatrix} \\
\hat{L}_{-} &= \frac{\Hbar}{2}
\begin{bmatrix}
0 & 0 \\
1 & 0
\end{bmatrix}.
\end{aligned}
\end{equation}

Rearranging we find the Pauli matrices

\begin{equation}\label{eqn:qmLecture15:200}
\hat{L}_k = \inv{2} \Hbar \sigma_i.
\end{equation}

Noting that \( \lr{ \Bsigma \cdot \ncap }^2 = 1 \), and \( \lr{\Bsigma \cdot \ncap }^3 = \Bsigma \cdot \ncap \), the rotation matrix is

\begin{equation}\label{eqn:qmLecture15:220}
e^{ i \Bsigma \cdot \ncap \phi/2 } \ket{\inv{2}, m} = \lr{ \cos( \phi/2 ) + i \Bsigma \cdot \ncap \sin(\phi/2) } \ket{\inv{2}, m}.
\end{equation}

The steps are

  1. Enumerate the states.
    \begin{equation}\label{eqn:qmLecture15:140}
    j_1 = \inv{2} \leftrightarrow\, \mbox{2 states (dimension of irrep = 2)}
    \end{equation}

  2. Construct the \( \hat{\BL} \) matrices.
  3. Construct \( d_{m m’}^j(\ncap, \phi) \).

Angular momentum operator in space representation

For \( L = 1 \) it turns out that the rotation matrices turn out to be the 3D rotation matrices. In the space representation

\begin{equation}\label{eqn:qmLecture15:240}
\BL = \Br \cross \Bp,
\end{equation}

the coordinates of the operator are

\begin{equation}\label{eqn:qmLecture15:260}
\hat{L}_k = i \epsilon_{k m n} r_m \lr{ -i \Hbar \PD{r_n}{} }
\end{equation}

We see that scaling \( \Br \rightarrow \alpha \Br \) does not change this operator, allowing for an angular representation \( \hat{L}_k(\theta, \phi) \) that have the form

\begin{equation}\label{eqn:qmLecture15:280}
\begin{aligned}
\hat{L}_z &= -i \Hbar \PD{\phi}{} \\
\hat{L}_{\pm} &= \Hbar \lr{ \pm \PD{\theta}{} + i \cot \theta \PD{\phi}{} }.
\end{aligned}
\end{equation}

Here \( \theta \) and \( \phi \) are the polar and azimuthal angles respectively as illustrated in fig. 2.

fig. 2. Spherical coordinate convention.

fig. 2. Spherical coordinate convention.

The equivalent wave function representation of the problem is

\begin{equation}\label{eqn:qmLecture15:300}
\begin{aligned}
\hat{\BL} Y_{lm}(\theta, \phi) &= \Hbar^2 l (l + 1) Y_{lm}(\theta, \phi) \\
\hat{L}_z Y_{lm}(\theta, \phi) &= \Hbar m Y_{lm}(\theta, \phi) \\
\end{aligned}
\end{equation}

One can find these functions

\begin{equation}\label{eqn:qmLecture15:320}
Y_{lm}(\theta, \phi) = P_{l, m}(\cos \theta) e^{i m \phi},
\end{equation}

where \( P_{l, m}(\cos \theta) \) are called the associated Legendre polynomials. This can be applied whenever we have

\begin{equation}\label{eqn:qmLecture15:340}
\antisymmetric{H}{\hat{L}_k} = 0.
\end{equation}

where all the eigenfunctions will have the form

\begin{equation}\label{eqn:qmLecture15:360}
\Psi(r, \theta, \phi) = R(r) Y_{lm}(\theta, \phi).
\end{equation}

Addition of angular momentum

Since \( \hat{\BL} \) is a vector we expect to be able to add angular momentum in some way similar to the addition of classical vectors as illustrated in fig. 3.

fig. 3. Classical vector addition.

fig. 3. Classical vector addition.

When we have a potential that depends only on the difference in position \( V(\Br_1 – \Br_2) \) then we know from classical problems it is effective to work in center of mass coordinates

\begin{equation}\label{eqn:qmLecture15:380}
\begin{aligned}
\hat{\BR}_{\textrm{cm}} &= \frac{\hat{\Br}_1 + \hat{\Br}_2}{2} \\
\hat{\BP}_{\textrm{cm}} &= \hat{\Bp}_1 + \hat{\Bp}_2
\end{aligned}
\end{equation}

where

\begin{equation}\label{eqn:qmLecture15:400}
\antisymmetric{\hat{R}_i}{\hat{P}_j} = i \Hbar \delta_{ij}.
\end{equation}

Given

\begin{equation}\label{eqn:qmLecture15:420}
\hat{\BL}_1 + \hat{\BL}_2 = \hat{\BL}_{\textrm{tot}},
\end{equation}

do we have
\begin{equation}\label{eqn:qmLecture15:440}
\antisymmetric{
\hat{L}_{\textrm{tot}, i}
}{
\hat{L}_{\textrm{tot}, j}
}
= i \Hbar \epsilon_{i j k} \hat{L}_{\textrm{tot}, k} ?
\end{equation}

That is

\begin{equation}\label{eqn:qmLecture15:460}
\antisymmetric{\hat{L}_{1,i} + \hat{L}_{1,j}}{\hat{L}_{2,i} + \hat{L}_{2,j}} = i \Hbar \epsilon_{i j k} \lr{ \hat{L}_{1,k} + \hat{L}_{1,k} }
\end{equation}

FIXME: Right at the end of the lecture, there was a mention of something about whether or not \( \hat{\BL}_1^2 \) and \( \hat{L}_{1,z} \) were sharply defined, but I missed it. Ask about this if not covered in the next lecture.

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

PHY1520H Graduate Quantum Mechanics. Lecture 14: Angular momentum (cont.). Taught by Prof. Arun Paramekanti

November 11, 2015 phy1520 , , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course PHY1520, Graduate Quantum Mechanics, taught by Prof. Paramekanti, covering [1] chap. 3 content.

Review: Angular momentum

Given eigenket \( \ket{a, b} \), where

\begin{equation}\label{eqn:qmLecture14:20}
\begin{aligned}
\hat{\BL}^2 \ket{a, b} &= \Hbar^2 a \ket{a,b} \\
\hat{L}_z \ket{a, b} &= \Hbar b \ket{a,b}
\end{aligned}
\end{equation}

We were looking for

\begin{equation}\label{eqn:qmLecture14:40}
\hat{L}_{x,y} \ket{a,b} = \sum_{b’} \mathcal{A}^{x,y}_{a; b, b’} \ket{a,b’},
\end{equation}

by applying

\begin{equation}\label{eqn:qmLecture14:60}
\hat{L}_{\pm} = \hat{L}_x \pm i \hat{L}_y.
\end{equation}

We found

\begin{equation}\label{eqn:qmLecture14:80}
\hat{L}_{\pm} \propto \ket{a, b \pm 1}.
\end{equation}

Let

\begin{equation}\label{eqn:qmLecture14:100}
\ket{\phi_\pm} = \hat{L}_{\pm} \ket{a, b}.
\end{equation}

We want

\begin{equation}\label{eqn:qmLecture14:120}
\braket{\phi_\pm}{\phi_\pm} \ge 0,
\end{equation}

or
\begin{equation}\label{eqn:qmLecture14:140}
\begin{aligned}
\bra{a,b} \hat{L}_{+} \hat{L}_{-} \ket{a, b} &\ge 0 \\
\bra{a,b} \hat{L}_{-} \hat{L}_{+} \ket{a, b} &\ge 0
\end{aligned}
\end{equation}

We found

\begin{equation}\label{eqn:qmLecture14:160}
\begin{aligned}
\hat{L}_{+} \hat{L}_{-} =
\lr{ \hat{L}_x + i \hat{L}_y } \lr{ \hat{L}_x – i \hat{L}_y }
&= \lr{ \hat{\BL}^2 – \hat{L}_z^2 } -i \antisymmetric{\hat{L}_x}{\hat{L}_y} \\
&= \lr{ \hat{\BL}^2 – \hat{L}_z^2 } -i \lr{ i \Hbar \hat{L}_z } \\
&= \lr{ \hat{\BL}^2 – \hat{L}_z^2 } + \Hbar \hat{L}_z,
\end{aligned}
\end{equation}

so

\begin{equation}\label{eqn:qmLecture14:180}
\bra{a,b} \hat{L}_{+} \hat{L}_{-} \ket{a, b}
=
\expectation{ \hat{\BL}^2 – \hat{L}_z^2 + \Hbar \hat{L}_z }.
\end{equation}

Similarly
\begin{equation}\label{eqn:qmLecture14:200}
\bra{a,b} \hat{L}_{-} \hat{L}_{+} \ket{a, b}
=
\expectation{ \hat{\BL}^2 – \hat{L}_z^2 – \Hbar \hat{L}_z }.
\end{equation}

Constraints

\begin{equation}\label{eqn:qmLecture14:220}
\begin{aligned}
a – b^2 + b &\ge 0 \\
a – b^2 – b &\ge 0
\end{aligned}
\end{equation}

If these are satisfied at the equality extreme we have

\begin{equation}\label{eqn:qmLecture14:240}
\begin{aligned}
b_{\textrm{max}} \lr{ b_{\textrm{max}} + 1 } &= a \\
b_{\textrm{min}} \lr{ b_{\textrm{min}} – 1 } &= a.
\end{aligned}
\end{equation}

Rearranging this to solve, we can rewrite the equality as

\begin{equation}\label{eqn:qmLecture14:680}
\lr{ b_{\textrm{max}} + \inv{2} }^2 – \inv{4} = \lr{ b_{\textrm{min}} – \inv{2} }^2 – \inv{4},
\end{equation}

which has solutions at

\begin{equation}\label{eqn:qmLecture14:700}
b_{\textrm{max}} + \inv{2} = \pm \lr{ b_{\textrm{min}} – \inv{2} }.
\end{equation}

One of the solutions is

\begin{equation}\label{eqn:qmLecture14:260}
-b_{\textrm{min}} = b_{\textrm{max}}.
\end{equation}

The other solution is \( b_{\textrm{max}} = b_{\textrm{min}} – 1 \), which we discard.

The final constraint is therefore

\begin{equation}\label{eqn:qmLecture14:280}
\boxed{
– b_{\textrm{max}} \le b \le b_{\textrm{max}},
}
\end{equation}

and

\begin{equation}\label{eqn:qmLecture14:320}
\begin{aligned}
\hat{L}_{+} \ket{a, b_{\textrm{max}}} &= 0 \\
\hat{L}_{-} \ket{a, b_{\textrm{min}}} &= 0
\end{aligned}
\end{equation}

If we had the sequence, which must terminate at \( b_{\textrm{min}} \) or else it will go on forever

\begin{equation}\label{eqn:qmLecture14:340}
\ket{a, b_{\textrm{max}}}
\overset{\hat{L}_{-}}{\rightarrow}
\ket{a, b_{\textrm{max}} – 1}
\overset{\hat{L}_{-}}{\rightarrow}
\ket{a, b_{\textrm{max}} – 2}
\cdots
\overset{\hat{L}_{-}}{\rightarrow}
\ket{a, b_{\textrm{min}}},
\end{equation}

then we know that \( b_{\textrm{max}} – b_{\textrm{min}} \in \mathbb{Z} \), or

\begin{equation}\label{eqn:qmLecture14:360}
b_{\textrm{max}} – n = b_{\textrm{min}} = -b_{\textrm{max}}
\end{equation}

or

\begin{equation}\label{eqn:qmLecture14:380}
b_{\textrm{max}} = \frac{n}{2},
\end{equation}

this is either an integer or a \( 1/2 \) odd integer, depending on whether \( n \) is even or odd. These are called “orbital” or “spin” respectively.

The convention is to write

\begin{equation}\label{eqn:qmLecture14:400}
\begin{aligned}
b_{\textrm{max}} &= j \\
a &= j(j + 1).
\end{aligned}
\end{equation}

so for \( m \in -j, -j + 1, \cdots, +j \)

\begin{equation}\label{eqn:qmLecture14:420}
\boxed{
\begin{aligned}
\hat{\BL}^2 \ket{j, m} &= \Hbar^2 j (j + 1) \ket{j, m} \\
L_z \ket{j, m} &= \Hbar m \ket{j, m}.
\end{aligned}
}
\end{equation}

Schwinger’s Harmonic oscillator representation of angular momentum operators.

In [2] a powerful method for describing angular momentum with harmonic oscillators was introduced, which will be outlined here. The question is whether we can construct a set of harmonic oscillators that allows a mapping from

\begin{equation}\label{eqn:qmLecture14:460}
\hat{L}_{+} \leftrightarrow a^{+}?
\end{equation}

Picture two harmonic oscillators, one with states counted from one zero towards \( \infty \) and another with states counted from a different zero towards \( -\infty \), as pictured in fig. 1.

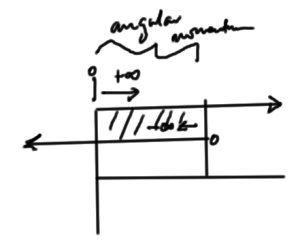
fig. 1. Overlapping SHO domains

fig. 1. Overlapping SHO domains

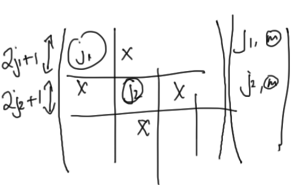
Is it possible that such an overlapping set of harmonic oscillators can provide the properties of the angular momentum operators? Let’s relabel the counting so that we have two sets of positive counted SHO systems, each counted in a positive direction as sketched in fig. 2.

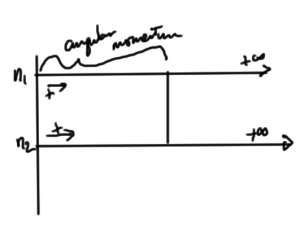
fig. 2. Relabeling the counting for overlapping SHO systems

fig. 2. Relabeling the counting for overlapping SHO systems

It turns out that given a constraint there the number of ways to distribute particles between a pair of SHO systems, the process that can be viewed as reproducing the angular momentum action is a transfer of particles from one harmonic oscillator to the other. For \( \hat{L}_z = +j \)

\begin{equation}\label{eqn:qmLecture14:480}
\begin{aligned}
n_1 &= n_{\textrm{max}} \\
n_2 &= 0,
\end{aligned}
\end{equation}

and for \( \hat{L}_z = -j \)

\begin{equation}\label{eqn:qmLecture14:500}
\begin{aligned}
n_1 &= 0 \\
n_2 &= n_{\textrm{max}}.
\end{aligned}
\end{equation}

We can make the identifications

\begin{equation}\label{eqn:qmLecture14:520}
\hat{L}_z = \lr{ n_1 – n_2 } \frac{\Hbar}{2},
\end{equation}

and
\begin{equation}\label{eqn:qmLecture14:540}
j = \inv{2} n_{\textrm{max}},
\end{equation}

or

\begin{equation}\label{eqn:qmLecture14:560}
n_1 + n_2 = \text{fixed} = n_{\textrm{max}}
\end{equation}

Changes that keep \( n_1 + n_2 \) fixed are those that change \( n_1 \), \( n_2 \) by \( +1 \) or \( -1 \) respectively, as sketched in fig. 3.

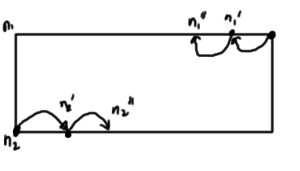
fig. 3. Number conservation constraint.

fig. 3. Number conservation constraint.

Can we make an identification that takes

\begin{equation}\label{eqn:qmLecture14:580}
\ket{n_1, n_2} \overset{\hat{L}_{-}}{\rightarrow} \ket{n_1 – 1, n_2 + 1}?
\end{equation}

What operator in the SHO problem has this effect? Let’s try

\boxedEquation{eqn:qmLecture14:620}{
\begin{aligned}
\hat{L}_{-} &= \Hbar a_2^\dagger a_1 \\
\hat{L}_{+} &= \Hbar a_1^\dagger a_2 \\
\hat{L}_z &= \frac{\Hbar}{2} \lr{ n_1 – n_2 }
\end{aligned}
}

Is this correct? Do we need to make any scalar adjustments? We want

\begin{equation}\label{eqn:qmLecture14:640}
\antisymmetric{\hat{L}_z}{\hat{L}_{\pm}} = \pm \Hbar \hat{L}_{\pm}.
\end{equation}

First check this with the \( \hat{L}_{+} \) commutator

\begin{equation}\label{eqn:qmLecture14:660}
\begin{aligned}
\antisymmetric{\hat{L}_z}{\hat{L}_{+}}
&=
\inv{2} \Hbar^2 \antisymmetric{ n_1 – n_2}{a_1^\dagger a_2 } \\
&=
\inv{2} \Hbar^2 \antisymmetric{ a_1^\dagger a_1 – a_2^\dagger a_2 }{a_1^\dagger a_2 } \\
&=
\inv{2} \Hbar^2
\lr{
\antisymmetric{ a_1^\dagger a_1 }{a_1^\dagger a_2 }
-\antisymmetric{ a_2^\dagger a_2 }{a_1^\dagger a_2 }
} \\
&=
\inv{2} \Hbar^2
\lr{
a_2 \antisymmetric{ a_1^\dagger a_1 }{a_1^\dagger }
-a_1^\dagger \antisymmetric{ a_2^\dagger a_2 }{a_2 }
}.
\end{aligned}
\end{equation}

But

\begin{equation}\label{eqn:qmLecture14:720}
\begin{aligned}
\antisymmetric{ a^\dagger a }{a^\dagger }
&=
a^\dagger a
a^\dagger
–
a^\dagger
a^\dagger a \\
&=
a^\dagger \lr{ 1 +
a^\dagger a}
–
a^\dagger
a^\dagger a \\
&=
a^\dagger,
\end{aligned}
\end{equation}

and
\begin{equation}\label{eqn:qmLecture14:740}
\begin{aligned}
\antisymmetric{ a^\dagger a }{a}
&=
a^\dagger a a
-a a^\dagger a \\
&=
a^\dagger a a
-\lr{ 1 + a^\dagger a } a \\
&=
-a,
\end{aligned}
\end{equation}

so
\begin{equation}\label{eqn:qmLecture14:760}
\antisymmetric{\hat{L}_z}{\hat{L}_{+}} = \Hbar^2 a_2 a_1^\dagger = \Hbar \hat{L}_{+},
\end{equation}

as desired. Similarly

\begin{equation}\label{eqn:qmLecture14:780}
\begin{aligned}
\antisymmetric{\hat{L}_z}{\hat{L}_{-}}
&=
\inv{2} \Hbar^2 \antisymmetric{ n_1 – n_2}{a_2^\dagger a_1 } \\
&=
\inv{2} \Hbar^2 \antisymmetric{ a_1^\dagger a_1 – a_2^\dagger a_2 }{a_2^\dagger a_1 } \\
&=
\inv{2} \Hbar^2 \lr{
a_2^\dagger \antisymmetric{ a_1^\dagger a_1 }{a_1 }
– a_1 \antisymmetric{ a_2^\dagger a_2 }{a_2^\dagger }
} \\
&=
\inv{2} \Hbar^2 \lr{
a_2^\dagger (-a_1)
– a_1 a_2^\dagger
} \\
&=
– \Hbar^2 a_2^\dagger a_1 \\
&=
– \Hbar \hat{L}_{-}.
\end{aligned}
\end{equation}

With

\begin{equation}\label{eqn:qmLecture14:800}
\begin{aligned}
j &= \frac{n_1 + n_2}{2} \\
m &= \frac{n_1 – n_2}{2} \\
\end{aligned}
\end{equation}

We can make the identification

\begin{equation}\label{eqn:qmLecture14:820}
\ket{n_1, n_2} = \ket{ j+ m , j – m}.
\end{equation}

Another way

With

\begin{equation}\label{eqn:qmLecture14:840}
\hat{L}_{+} \ket{j, m} = d_{j,m}^{+} \ket{j, m+1}
\end{equation}

or

\begin{equation}\label{eqn:qmLecture14:860}
\Hbar a_1^\dagger a_2 \ket{j + m, j-m} = d_{j,m}^{+} \ket{ j + m + 1, j- m-1},
\end{equation}

we can seek this factor \( d_{j,m}^{+} \) by operating with \( \hat{L}_{+} \)

\begin{equation}\label{eqn:qmLecture14:880}
\begin{aligned}
\hat{L}_{+} \ket{j, m}
&=
\Hbar a_1^\dagger a_2 \ket{n_1, n_2} \\
&=
\Hbar a_1^\dagger a_2 \ket{j+m,j-m} \\
&=
\Hbar \sqrt{ n + 1 } \sqrt{n_2} \ket{j+m +1,j-m-1} \\
&=
\Hbar \sqrt{ \lr{ j+ m + 1}\lr{ j – m } } \ket{j+m +1,j-m-1}
\end{aligned}
\end{equation}

That gives
\begin{equation}\label{eqn:qmLecture14:900}
\begin{aligned}
d_{j,m}^{+} &= \Hbar \sqrt{\lr{ j – m } \lr{ j+ m + 1} } \\
d_{j,m}^{-} &= \Hbar \sqrt{\lr{ j + m } \lr{ j- m + 1} }.
\end{aligned}
\end{equation}

This equivalence can be used to model spin interaction in crystals as harmonic oscillators. This equivalence of lattice vibrations and spin oscillations is called “spin waves”.

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

[2] J Schwinger. Quantum theory of angular momentum. biedenharn l., van dam h., editors, 1955. URL http://www.ifi.unicamp.br/ cabrera/teaching/paper_schwinger.pdf.