Lagrangian

A multivector Lagrangian for Maxwell’s equation, w/ electric and magnetic current density four-vector sources

June 29, 2022 math and physics play , , , , , , , ,

[Click here for a PDF version of this and previous related posts .]

Initially I had trouble generalizing the multivector Lagrangian to include both the electric and magnetic sources without using two independent potentials. However, this can be done, provided one is careful enough. Recall that we found that a useful formulation for the field in terms of two potentials is
\begin{equation}\label{eqn:maxwellLagrangian:2050}
F = F_{\mathrm{e}} + I F_{\mathrm{m}},
\end{equation}
where
\begin{equation}\label{eqn:maxwellLagrangian:2070}
\begin{aligned}
F_{\mathrm{e}} = \grad \wedge A \\
F_{\mathrm{m}} = \grad \wedge K,
\end{aligned}
\end{equation}
and where \( A, K \) are arbitrary four-vector potentials.
Use of two potentials allowed us to decouple Maxwell’s equations into two separate gradient equations. We don’t want to do that now, but let’s see how we can combine the two fields into a single multivector potential. Letting the gradient act bidirectionally, and introducing a dummy grade-two selection into the mix, we have
\begin{equation}\label{eqn:maxwellLagrangian:2090}
\begin{aligned}
F
&= \rgrad \wedge A + I \lr{ \rgrad \wedge K } \\
&= – A \wedge \lgrad – I \lr{ K \wedge \lgrad } \\
&= -\gpgradetwo{ A \wedge \lgrad + I \lr{ K \wedge \lgrad } } \\
&= -\gpgradetwo{ A \lgrad + I K \lgrad } \\
&= -\gpgradetwo{ \lr{ A + I K } \lgrad }.
\end{aligned}
\end{equation}
Now, we call
\begin{equation}\label{eqn:maxwellLagrangian:2110}
N = A + I K,
\end{equation}
(a 1,3 multivector), the multivector potential, and write the electromagnetic field not in terms of curls explicitly, but using a grade-2 selection filter
\begin{equation}\label{eqn:maxwellLagrangian:2130}
F = -\gpgradetwo{ N \lgrad }.
\end{equation}

We can now form the following multivector Lagrangian
\begin{equation}\label{eqn:maxwellLagrangian:2150}
\LL = \inv{2} F^2 – \gpgrade{ N \lr{ J – I M } }{0,4},
\end{equation}
and vary the action to (eventually) find our multivector Maxwell’s equation, without ever resorting to coordinates. We have
\begin{equation}\label{eqn:maxwellLagrangian:2170}
\begin{aligned}
\delta S
&= \int d^4 x \inv{2} \lr{ \lr{ \delta F } F + F \lr{ \delta F } } – \gpgrade{ \delta N \lr{ J – I M } }{0,4} \\
&= \int d^4 x \gpgrade{ \lr{ \delta F } F – \lr{ \delta N } \lr{ J – I M } }{0,4} \\
&= \int d^4 x \gpgrade{ -\gpgradetwo{ \lr{ \delta N} \lgrad } F – \lr{ \delta N } \lr{ J – I M } }{0,4} \\
&= \int d^4 x \gpgrade{ -\gpgradetwo{ \lr{ \delta N} \lrgrad } F +\gpgradetwo{ \lr{ \delta N} \rgrad } F – \lr{ \delta N } \lr{ J – I M } }{0,4}.
\end{aligned}
\end{equation}
The \( \lrgrad \) term can be evaluated using the fundamential theorem of GC, and will be zero, as \( \delta N = 0 \) on the boundary. Let’s look at the next integrand term a bit more carefully
\begin{equation}\label{eqn:maxwellLagrangian:2190}
\begin{aligned}
\gpgrade{ \gpgradetwo{ \lr{ \delta N} \rgrad } F }{0,4}
&=
\gpgrade{ \gpgradetwo{ \lr{ \lr{ \delta A } + I \lr{ \delta K } } \rgrad } F }{0,4} \\
&=
\gpgrade{ \lr{ \lr{\delta A} \wedge \rgrad + I \lr{ \lr{ \delta K } \wedge \rgrad }} F }{0,4} \\
&=
\gpgrade{ \lr{\delta A} \rgrad F – \lr{ \lr{\delta A} \cdot \rgrad} F + I \lr{ \delta K } \rgrad F – I \lr{ \lr{ \delta K } \cdot \rgrad} F }{0,4} \\
&=
\gpgrade{ \lr{\delta A} \rgrad F + I \lr{ \delta K } \rgrad F }{0,4} \\
&=
\gpgrade{ \lr{ \lr{\delta A} + I \lr{ \delta K} } \rgrad F }{0,4} \\
&=
\gpgrade{ \lr{ \delta N} \rgrad F }{0,4},
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:maxwellLagrangian:2210}
\begin{aligned}
\delta S
&= \int d^4 x \gpgrade{ \lr{ \delta N} \rgrad F – \lr{ \delta N } \lr{ J – I M } }{0,4} \\
&= \int d^4 x \gpgrade{ \lr{ \delta N} \lr{ \rgrad F – \lr{ J – I M } } }{0,4}.
\end{aligned}
\end{equation}
for this to be zero for all variations \( \delta N \) of the 1,3-multivector potential \( N \), we must have
\begin{equation}\label{eqn:maxwellLagrangian:2230}
\grad F = J – I M.
\end{equation}
This is Maxwell’s equation, as desired, including both electric and (if desired) magnetic sources.

A multivector Lagrangian for Maxwell’s equation: A summary of previous exploration.

June 21, 2022 math and physics play , , , , , , , , , , , , , , , , , , , ,

This summarizes the significant parts of the last 8 blog posts.

[Click here for a PDF version of this post]

STA form of Maxwell’s equation.

Maxwell’s equations, with electric and fictional magnetic sources (useful for antenna theory and other engineering applications), are
\begin{equation}\label{eqn:maxwellLagrangian:220}
\begin{aligned}
\spacegrad \cdot \BE &= \frac{\rho}{\epsilon} \\
\spacegrad \cross \BE &= – \BM – \mu \PD{t}{\BH} \\
\spacegrad \cdot \BH &= \frac{\rho_\txtm}{\mu} \\
\spacegrad \cross \BH &= \BJ + \epsilon \PD{t}{\BE}.
\end{aligned}
\end{equation}
We can assemble these into a single geometric algebra equation,
\begin{equation}\label{eqn:maxwellLagrangian:240}
\lr{ \spacegrad + \inv{c} \PD{t}{} } F = \eta \lr{ c \rho – \BJ } + I \lr{ c \rho_{\mathrm{m}} – \BM },
\end{equation}
where \( F = \BE + \eta I \BH = \BE + I c \BB \), \( c = 1/\sqrt{\mu\epsilon}, \eta = \sqrt{(\mu/\epsilon)} \).

By multiplying through by \( \gamma_0 \), making the identification \( \Be_k = \gamma_k \gamma_0 \), and
\begin{equation}\label{eqn:maxwellLagrangian:300}
\begin{aligned}
J^0 &= \frac{\rho}{\epsilon}, \quad J^k = \eta \lr{ \BJ \cdot \Be_k }, \quad J = J^\mu \gamma_\mu \\
M^0 &= c \rho_{\mathrm{m}}, \quad M^k = \BM \cdot \Be_k, \quad M = M^\mu \gamma_\mu \\
\grad &= \gamma^\mu \partial_\mu,
\end{aligned}
\end{equation}
we find the STA form of Maxwell’s equation, including magnetic sources
\begin{equation}\label{eqn:maxwellLagrangian:320}
\grad F = J – I M.
\end{equation}

Decoupling the electric and magnetic fields and sources.

We can utilize two separate four-vector potential fields to split Maxwell’s equation into two parts. Let
\begin{equation}\label{eqn:maxwellLagrangian:1740}
F = F_{\mathrm{e}} + I F_{\mathrm{m}},
\end{equation}
where
\begin{equation}\label{eqn:maxwellLagrangian:1760}
\begin{aligned}
F_{\mathrm{e}} &= \grad \wedge A \\
F_{\mathrm{m}} &= \grad \wedge K,
\end{aligned}
\end{equation}
and \( A, K \) are independent four-vector potential fields. Plugging this into Maxwell’s equation, and employing a duality transformation, gives us two coupled vector grade equations
\begin{equation}\label{eqn:maxwellLagrangian:1780}
\begin{aligned}
\grad \cdot F_{\mathrm{e}} – I \lr{ \grad \wedge F_{\mathrm{m}} } &= J \\
\grad \cdot F_{\mathrm{m}} + I \lr{ \grad \wedge F_{\mathrm{e}} } &= M.
\end{aligned}
\end{equation}
However, since \( \grad \wedge F_{\mathrm{m}} = \grad \wedge F_{\mathrm{e}} = 0 \), by construction, the curls above are killed. We may also add in \( \grad \wedge F_{\mathrm{e}} = 0 \) and \( \grad \wedge F_{\mathrm{m}} = 0 \) respectively, yielding two independent gradient equations
\begin{equation}\label{eqn:maxwellLagrangian:1810}
\begin{aligned}
\grad F_{\mathrm{e}} &= J \\
\grad F_{\mathrm{m}} &= M,
\end{aligned}
\end{equation}
one for each of the electric and magnetic sources and their associated fields.

Tensor formulation.

The electromagnetic field \( F \), is a vector-bivector multivector in the multivector representation of Maxwell’s equation, but is a bivector in the STA representation. The split of \( F \) into it’s electric and magnetic field components is observer dependent, but we may write it without reference to a specific observer frame as
\begin{equation}\label{eqn:maxwellLagrangian:1830}
F = \inv{2} \gamma_\mu \wedge \gamma_\nu F^{\mu\nu},
\end{equation}
where \( F^{\mu\nu} \) is an arbitrary antisymmetric 2nd rank tensor. Maxwell’s equation has a vector and trivector component, which may be split out explicitly using grade selection, to find
\begin{equation}\label{eqn:maxwellLagrangian:360}
\begin{aligned}
\grad \cdot F &= J \\
\grad \wedge F &= -I M.
\end{aligned}
\end{equation}
Further dotting and wedging these equations with \( \gamma^\mu \) allows for extraction of scalar relations
\begin{equation}\label{eqn:maxwellLagrangian:460}
\partial_\nu F^{\nu\mu} = J^{\mu}, \quad \partial_\nu G^{\nu\mu} = M^{\mu},
\end{equation}
where \( G^{\mu\nu} = -(1/2) \epsilon^{\mu\nu\alpha\beta} F_{\alpha\beta} \) is also an antisymmetric 2nd rank tensor.

If we treat \( F^{\mu\nu} \) and \( G^{\mu\nu} \) as independent fields, this pair of equations is the coordinate equivalent to \ref{eqn:maxwellLagrangian:1760}, also decoupling the electric and magnetic source contributions to Maxwell’s equation.

Coordinate representation of the Lagrangian.

As observed above, we may choose to express the decoupled fields as curls \( F_{\mathrm{e}} = \grad \wedge A \) or \( F_{\mathrm{m}} = \grad \wedge K \). The coordinate expansion of either field component, given such a representation, is straight forward. For example
\begin{equation}\label{eqn:maxwellLagrangian:1850}
\begin{aligned}
F_{\mathrm{e}}
&= \lr{ \gamma_\mu \partial^\mu } \wedge \lr{ \gamma_\nu A^\nu } \\
&= \inv{2} \lr{ \gamma_\mu \wedge \gamma_\nu } \lr{ \partial^\mu A^\nu – \partial^\nu A^\mu }.
\end{aligned}
\end{equation}

We make the identification \( F^{\mu\nu} = \partial^\mu A^\nu – \partial^\nu A^\mu \), the usual definition of \( F^{\mu\nu} \) in the tensor formalism. In that tensor formalism, the Maxwell Lagrangian is
\begin{equation}\label{eqn:maxwellLagrangian:1870}
\LL = – \inv{4} F_{\mu\nu} F^{\mu\nu} – A_\mu J^\mu.
\end{equation}
We may show this though application of the Euler-Lagrange equations
\begin{equation}\label{eqn:maxwellLagrangian:600}
\PD{A_\mu}{\LL} = \partial_\nu \PD{(\partial_\nu A_\mu)}{\LL}.
\end{equation}
\begin{equation}\label{eqn:maxwellLagrangian:1930}
\begin{aligned}
\PD{(\partial_\nu A_\mu)}{\LL}
&= -\inv{4} (2) \lr{ \PD{(\partial_\nu A_\mu)}{F_{\alpha\beta}} } F^{\alpha\beta} \\
&= -\inv{2} \delta^{[\nu\mu]}_{\alpha\beta} F^{\alpha\beta} \\
&= -\inv{2} \lr{ F^{\nu\mu} – F^{\mu\nu} } \\
&= F^{\mu\nu}.
\end{aligned}
\end{equation}
So \( \partial_\nu F^{\nu\mu} = J^\mu \), the equivalent of \( \grad \cdot F = J \), as expected.

Coordinate-free representation and variation of the Lagrangian.

Because
\begin{equation}\label{eqn:maxwellLagrangian:200}
F^2 =
-\inv{2}
F^{\mu\nu} F_{\mu\nu}
+
\lr{ \gamma_\alpha \wedge \gamma^\beta }
F_{\alpha\mu}
F^{\beta\mu}
+
\frac{I}{4}
\epsilon_{\mu\nu\alpha\beta} F^{\mu\nu} F^{\alpha\beta},
\end{equation}
we may express the Lagrangian \ref{eqn:maxwellLagrangian:1870} in a coordinate free representation
\begin{equation}\label{eqn:maxwellLagrangian:1890}
\LL = \inv{2} F \cdot F – A \cdot J,
\end{equation}
where \( F = \grad \wedge A \).

We will now show that it is also possible to apply the variational principle to the following multivector Lagrangian
\begin{equation}\label{eqn:maxwellLagrangian:1910}
\LL = \inv{2} F^2 – A \cdot J,
\end{equation}
and recover the geometric algebra form \( \grad F = J \) of Maxwell’s equation in it’s entirety, including both vector and trivector components in one shot.

We will need a few geometric algebra tools to do this.

The first such tool is the notational freedom to let the gradient act bidirectionally on multivectors to the left and right. We will designate such action with over-arrows, sometimes also using braces to limit the scope of the action in question. If \( Q, R \) are multivectors, then the bidirectional action of the gradient in a \( Q, R \) sandwich is
\begin{equation}\label{eqn:maxwellLagrangian:1950}
\begin{aligned}
Q \lrgrad R
&= Q \lgrad R + Q \rgrad R \\
&= \lr{ Q \gamma^\mu \lpartial_\mu } R + Q \lr{ \gamma^\mu \rpartial_\mu R } \\
&= \lr{ \partial_\mu Q } \gamma^\mu R + Q \gamma^\mu \lr{ \partial_\mu R }.
\end{aligned}
\end{equation}
In the final statement, the partials are acting exclusively on \( Q \) and \( R \) respectively, but the \( \gamma^\mu \) factors must remain in place, as they do not necessarily commute with any of the multivector factors.

This bidirectional action is a critical aspect of the Fundamental Theorem of Geometric calculus, another tool that we will require. The specific form of that theorem that we will utilize here is
\begin{equation}\label{eqn:maxwellLagrangian:1970}
\int_V Q d^4 \Bx \lrgrad R = \int_{\partial V} Q d^3 \Bx R,
\end{equation}
where \( d^4 \Bx = I d^4 x \) is the pseudoscalar four-volume element associated with a parameterization of space time. For our purposes, we may assume that parameterization are standard basis coordinates associated with the basis \( \setlr{ \gamma_0, \gamma_1, \gamma_2, \gamma_3 } \). The surface differential form \( d^3 \Bx \) can be given specific meaning, but we do not actually care what that form is here, as all our surface integrals will be zero due to the boundary constraints of the variational principle.

Finally, we will utilize the fact that bivector products can be split into grade \(0,4\) and \( 2 \) components using anticommutator and commutator products, namely, given two bivectors \( F, G \), we have
\begin{equation}\label{eqn:maxwellLagrangian:1990}
\begin{aligned}
\gpgrade{ F G }{0,4} &= \inv{2} \lr{ F G + G F } \\
\gpgrade{ F G }{2} &= \inv{2} \lr{ F G – G F }.
\end{aligned}
\end{equation}

We may now proceed to evaluate the variation of the action for our presumed Lagrangian
\begin{equation}\label{eqn:maxwellLagrangian:2010}
S = \int d^4 x \lr{ \inv{2} F^2 – A \cdot J }.
\end{equation}
We seek solutions of the variational equation \( \delta S = 0 \), that are satisfied for all variations \( \delta A \), where the four-potential variations \( \delta A \) are zero on the boundaries of this action volume (i.e. an infinite spherical surface.)

We may start our variation in terms of \( F \) and \( A \)
\begin{equation}\label{eqn:maxwellLagrangian:1540}
\begin{aligned}
\delta S
&=
\int d^4 x \lr{ \inv{2} \lr{ \delta F } F + F \lr{ \delta F } } – \lr{ \delta A } \cdot J \\
&=
\int d^4 x \gpgrade{ \lr{ \delta F } F – \lr{ \delta A } J }{0,4} \\
&=
\int d^4 x \gpgrade{ \lr{ \grad \wedge \lr{\delta A} } F – \lr{ \delta A } J }{0,4} \\
&=
-\int d^4 x \gpgrade{ \lr{ \lr{\delta A} \lgrad } F – \lr{ \lr{ \delta A } \cdot \lgrad } F + \lr{ \delta A } J }{0,4} \\
&=
-\int d^4 x \gpgrade{ \lr{ \lr{\delta A} \lgrad } F + \lr{ \delta A } J }{0,4} \\
&=
-\int d^4 x \gpgrade{ \lr{\delta A} \lrgrad F – \lr{\delta A} \rgrad F + \lr{ \delta A } J }{0,4},
\end{aligned}
\end{equation}
where we have used arrows, when required, to indicate the directional action of the gradient.

Writing \( d^4 x = -I d^4 \Bx \), we have
\begin{equation}\label{eqn:maxwellLagrangian:1600}
\begin{aligned}
\delta S
&=
-\int_V d^4 x \gpgrade{ \lr{\delta A} \lrgrad F – \lr{\delta A} \rgrad F + \lr{ \delta A } J }{0,4} \\
&=
-\int_V \gpgrade{ -\lr{\delta A} I d^4 \Bx \lrgrad F – d^4 x \lr{\delta A} \rgrad F + d^4 x \lr{ \delta A } J }{0,4} \\
&=
\int_{\partial V} \gpgrade{ \lr{\delta A} I d^3 \Bx F }{0,4}
+ \int_V d^4 x \gpgrade{ \lr{\delta A} \lr{ \rgrad F – J } }{0,4}.
\end{aligned}
\end{equation}
The first integral is killed since \( \delta A = 0 \) on the boundary. The remaining integrand can be simplified to
\begin{equation}\label{eqn:maxwellLagrangian:1660}
\gpgrade{ \lr{\delta A} \lr{ \rgrad F – J } }{0,4} =
\gpgrade{ \lr{\delta A} \lr{ \grad F – J } }{0},
\end{equation}
where the grade-4 filter has also been discarded since \( \grad F = \grad \cdot F + \grad \wedge F = \grad \cdot F \) since \( \grad \wedge F = \grad \wedge \grad \wedge A = 0 \) by construction, which implies that the only non-zero grades in the multivector \( \grad F – J \) are vector grades. Also, the directional indicator on the gradient has been dropped, since there is no longer any ambiguity. We seek solutions of \( \gpgrade{ \lr{\delta A} \lr{ \grad F – J } }{0} = 0 \) for all variations \( \delta A \), namely
\begin{equation}\label{eqn:maxwellLagrangian:1620}
\boxed{
\grad F = J.
}
\end{equation}
This is Maxwell’s equation in it’s coordinate free STA form, found using the variational principle from a coordinate free multivector Maxwell Lagrangian, without having to resort to a coordinate expansion of that Lagrangian.

Lagrangian for fictitious magnetic sources.

The generalization of the Lagrangian to include magnetic charge and current densities can be as simple as utilizing two independent four-potential fields
\begin{equation}\label{eqn:maxwellLagrangian:n}
\LL = \inv{2} \lr{ \grad \wedge A }^2 – A \cdot J + \alpha \lr{ \inv{2} \lr{ \grad \wedge K }^2 – K \cdot M },
\end{equation}
where \( \alpha \) is an arbitrary multivector constant.

Variation of this Lagrangian provides two independent equations
\begin{equation}\label{eqn:maxwellLagrangian:1840}
\begin{aligned}
\grad \lr{ \grad \wedge A } &= J \\
\grad \lr{ \grad \wedge K } &= M.
\end{aligned}
\end{equation}
We may add these, scaling the second by \( -I \) (recall that \( I, \grad \) anticommute), to find
\begin{equation}\label{eqn:maxwellLagrangian:1860}
\grad \lr{ F_{\mathrm{e}} + I F_{\mathrm{m}} } = J – I M,
\end{equation}
which is \( \grad F = J – I M \), as desired.

It would be interesting to explore whether it is possible find Lagrangian that is dependent on a multivector potential, that would yield \( \grad F = J – I M \) directly, instead of requiring a superposition operation from the two independent solutions. One such possible potential is \( \tilde{A} = A – I K \), for which \( F = \gpgradetwo{ \grad \tilde{A} } = \grad \wedge A + I \lr{ \grad \wedge K } \). The author was not successful constructing such a Lagrangian.

More satisfying editing of classical mechanics notes.

November 3, 2020 math and physics play , , , , ,

I’ve purged about 30 pages of material related to field Lagrangian densities and Maxwell’s equation, replacing it with about 8 pages of new less incoherent material.

As before, I’ve physically ripped out all the pages that have been replaced, which is satisfying, and makes it easier to see what is left to review.

The new version is now reduced to 333 pages, close to a 100 page reduction from the original mess.  I may print myself a new physical copy, as I’ve moved things around so much that I have to search the latex to figure out where to make changes.

Gauge transformation in the Lorentz force Lagrangian.

November 2, 2020 Uncategorized , , ,

[Click here for a PDF of this post with nicer formatting]

Problem: Lorentz force gauge transformation.

Show that the gauge transformation \( A \rightarrow A + \grad \psi \) applied to the Lorentz force Lagrangian
\begin{equation}\label{eqn:gaugeLorentzSTA:20}
L = \inv{2} m v^2 + q A \cdot v/c,
\end{equation}
does not change the equations of motion.

Answer

The gauge transformed Lagrangian is
\begin{equation}\label{eqn:gaugeLorentzSTA:40}
L = \inv{2} m v^2 + q A \cdot v/c + \frac{q v}{c} \cdot \grad \phi.
\end{equation}
We know that the Lorentz force equations are obtained from the first two terms, so need only consider the effects of the new \( \phi \) dependent term on the action. First observe that
\begin{equation}\label{eqn:gaugeLorentzSTA:60}
v \cdot \grad \phi
=
\frac{dx^\mu}{d\tau} \PD{x^\mu}{\phi}
=
\frac{d \phi}{d\tau}.
\end{equation}
This means that the action is transformed to
\begin{equation}\label{eqn:gaugeLorentzSTA:80}
S
\rightarrow S + \frac{q}{c} \int d\tau \frac{d\phi}{d\tau}
= S + \frac{q}{c} \evalbar{\phi}{\Delta \tau}.
\end{equation}
As the action is evaluated over a fixed interval, the gauge transformation only changes the action by a constant, so the equations of motion are unchanged.

References

PHY2403H Quantum Field Theory. Lecture 4: Scalar action, least action principle, Euler-Lagrange equations for a field, canonical quantization. Taught by Prof. Erich Poppitz

September 23, 2018 phy2403 , , , , , , , , , , , , , , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

DISCLAIMER: Very rough notes from class. May have some additional side notes, but otherwise probably barely edited.

These are notes for the UofT course PHY2403H, Quantum Field Theory I, taught by Prof. Erich Poppitz fall 2018.

Principles (cont.)

  • Lorentz (Poincar\’e : Lorentz and spacetime translations)
  • locality
  • dimensional analysis
  • gauge invariance

These are the requirements for an action. We postulated an action that had the form
\begin{equation}\label{eqn:qftLecture4:20}
\int d^d x \partial_\mu \phi \partial^\mu \phi,
\end{equation}
called the “Kinetic term”, which mimics \( \int dt \dot{q}^2 \) that we’d see in quantum or classical mechanics. In principle there exists an infinite number of local Poincar\’e invariant terms that we can write. Examples:

  • \( \partial_\mu \phi \partial^\mu \phi \)
  • \( \partial_\mu \phi \partial_\nu \partial^\nu \partial^\mu \phi \)
  • \( \lr{\partial_\mu \phi \partial^\mu \phi}^2 \)
  • \( f(\phi) \partial_\mu \phi \partial^\mu \phi \)
  • \( f(\phi, \partial_\mu \phi \partial^\mu \phi) \)
  • \( V(\phi) \)

It turns out that nature (i.e. three spatial dimensions and one time dimension) is described by a finite number of terms. We will now utilize dimensional analysis to determine some of the allowed forms of the action for scalar field theories in \( d = 2, 3, 4, 5 \) dimensions. Even though the real world is only \( d = 4 \), some of the \( d < 4 \) theories are relevant in condensed matter studies, and \( d = 5 \) is just for fun (but also applies to string theories.)

With \( [x] \sim \inv{M} \) in natural units, we must define \([\phi]\) such that the kinetic term is dimensionless in d spacetime dimensions

\begin{equation}\label{eqn:qftLecture4:40}
\begin{aligned}
[d^d x] &\sim \inv{M^d} \\
[\partial_\mu] &\sim M
\end{aligned}
\end{equation}

so it must be that
\begin{equation}\label{eqn:qftLecture4:60}
[\phi] = M^{(d-2)/2}
\end{equation}

It will be easier to characterize the dimensionality of any given term by the power of the mass units, that is

\begin{equation}\label{eqn:qftLecture4:80}
\begin{aligned}
[\text{mass}] &= 1 \\
[d^d x] &= -d \\
[\partial_\mu] &= 1 \\
[\phi] &= (d-2)/2 \\
[S] &= 0.
\end{aligned}
\end{equation}
Since the action is
\begin{equation}\label{eqn:qftLecture4:100}
S = \int d^d x \lr{ \LL(\phi, \partial_\mu \phi) },
\end{equation}
and because action had dimensions of \( \Hbar \), so in natural units, it must be dimensionless, the Lagrangian density dimensions must be \( [d] \). We will abuse language in QFT and call the Lagrangian density the Lagrangian.

\( d = 2 \)

Because \( [\partial_\mu \phi \partial^\mu \phi ] = 2 \), the scalar field must be dimension zero, or in symbols
\begin{equation}\label{eqn:qftLecture4:120}
[\phi] = 0.
\end{equation}
This means that introducing any function \( f(\phi) = 1 + a \phi + b\phi^2 + c \phi^3 + \cdots \) is also dimensionless, and
\begin{equation}\label{eqn:qftLecture4:140}
[f(\phi) \partial_\mu \phi \partial^\mu \phi ] = 2,
\end{equation}
for any \( f(\phi) \). Another implication of this is that the a potential term in the Lagrangian \( [V(\phi)] = 0 \) needs a coupling constant of dimension 2. Letting \( \mu \) have mass dimensions, our Lagrangian must have the form
\begin{equation}\label{eqn:qftLecture4:160}
f(\phi) \partial_\mu \phi \partial^\mu \phi + \mu^2 V(\phi).
\end{equation}
An infinite number of coupling constants of positive mass dimensions for \( V(\phi) \) are also allowed. If we have higher order derivative terms, then we need to compensate for the negative mass dimensions. Example (still for \( d = 2 \)).
\begin{equation}\label{eqn:qftLecture4:180}
\LL =
f(\phi) \partial_\mu \phi \partial^\mu \phi + \mu^2 V(\phi) + \inv{{\mu’}^2}\partial_\mu \phi \partial_\nu \partial^\nu \partial^\mu \phi + \lr{ \partial_\mu \phi \partial^\mu \phi }^2 \inv{\tilde{\mu}^2}.
\end{equation}
The last two terms, called \underline{couplings} (i.e. any non-kinetic term), are examples of terms with negative mass dimension. There is an infinite number of those in any theory in any dimension.

Definitions

  • Couplings that are dimensionless are called (classically) marginal.
  • Couplings that have positive mass dimension are called (classically) relevant.
  • Couplings that have negative mass dimension are called (classically) irrelevant.

In QFT we are generally interested in the couplings that are measurable at long distances for some given energy. Classically irrelevant theories are generally not interesting in \( d > 2 \), so we are very lucky that we don’t live in three dimensional space. This means that we can get away with a finite number of classically marginal and relevant couplings in 3 or 4 dimensions. This was mentioned in the Wilczek’s article referenced in the class forum [1]\footnote{There’s currently more in that article that I don’t understand than I do, so it is hard to find it terribly illuminating.}

Long distance physics in any dimension is described by the marginal and relevant couplings. The irrelevant couplings die off at low energy. In two dimensions, a priori, an infinite number of marginal and relevant couplings are possible. 2D is a bad place to live!

\( d = 3 \)

Now we have
\begin{equation}\label{eqn:qftLecture4:200}
[\phi] = \inv{2}
\end{equation}
so that
\begin{equation}\label{eqn:qftLecture4:220}
[\partial_\mu \phi \partial^\mu \phi] = 3.
\end{equation}

A 3D Lagrangian could have local terms such as
\begin{equation}\label{eqn:qftLecture4:240}
\LL = \partial_\mu \phi \partial^\mu \phi + m^2 \phi^2 + \mu^{3/2} \phi^3 + \mu’ \phi^4
+ \lr{\mu”}{1/2} \phi^5
+ \lambda \phi^6.
\end{equation}
where \( m, \mu, \mu” \) all have mass dimensions, and \( \lambda \) is dimensionless. i.e. \( m, \mu, \mu” \) are relevant, and \( \lambda \) marginal. We stop at the sixth power, since any power after that will be irrelevant.

\( d = 4 \)

Now we have
\begin{equation}\label{eqn:qftLecture4:260}
[\phi] = 1
\end{equation}
so that
\begin{equation}\label{eqn:qftLecture4:280}
[\partial_\mu \phi \partial^\mu \phi] = 4.
\end{equation}

In this number of dimensions \( \phi^k \partial_\mu \phi \partial^\mu \) is an irrelevant coupling.

A 4D Lagrangian could have local terms such as
\begin{equation}\label{eqn:qftLecture4:300}
\LL = \partial_\mu \phi \partial^\mu \phi + m^2 \phi^2 + \mu \phi^3 + \lambda \phi^4.
\end{equation}
where \( m, \mu \) have mass dimensions, and \( \lambda \) is dimensionless. i.e. \( m, \mu \) are relevant, and \( \lambda \) is marginal.

\( d = 5 \)

Now we have
\begin{equation}\label{eqn:qftLecture4:320}
[\phi] = \frac{3}{2},
\end{equation}
so that
\begin{equation}\label{eqn:qftLecture4:340}
[\partial_\mu \phi \partial^\mu \phi] = 5.
\end{equation}

A 5D Lagrangian could have local terms such as
\begin{equation}\label{eqn:qftLecture4:360}
\LL = \partial_\mu \phi \partial^\mu \phi + m^2 \phi^2 + \sqrt{\mu} \phi^3 + \inv{\mu’} \phi^4.
\end{equation}
where \( m, \mu, \mu’ \) all have mass dimensions. In 5D there are no marginal couplings. Dimension 4 is the last dimension where marginal couplings exist. In condensed matter physics 4D is called the “upper critical dimension”.

From the point of view of particle physics, all the terms in the Lagrangian must be the ones that are relevant at long distances.

Least action principle (classical field theory).

Now we want to study 4D scalar theories. We have some action
\begin{equation}\label{eqn:qftLecture4:380}
S[\phi] = \int d^4 x \LL(\phi, \partial_\mu \phi).
\end{equation}

Let’s keep an example such as the following in mind
\begin{equation}\label{eqn:qftLecture4:400}
\LL = \underbrace{\inv{2} \partial_\mu \phi \partial^\mu \phi}_{\text{Kinetic term}} – \underbrace{m^2 \phi – \lambda \phi^4}_{\text{all relevant and marginal couplings}}.
\end{equation}
The even powers can be justified by assuming there is some symmetry that kills the odd powered terms.

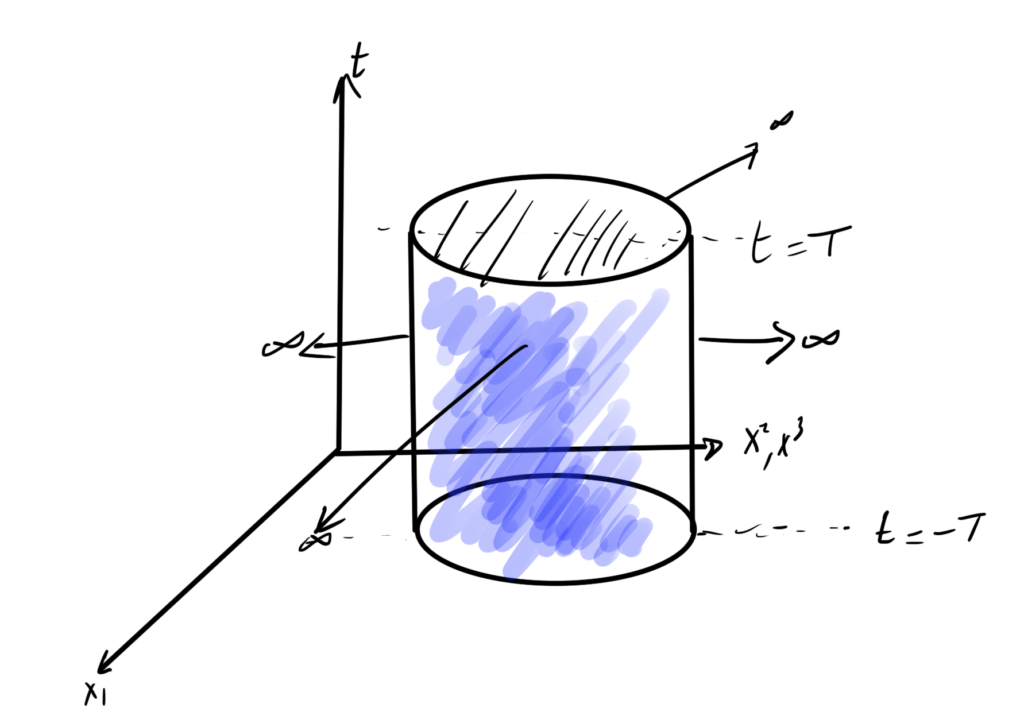
fig. 1. Cylindrical spacetime boundary.

We will be integrating over a space time region such as that depicted in fig. 1, where a cylindrical spatial cross section is depicted that we allow to tend towards infinity. We demand that the field is fixed on the infinite spatial boundaries. The easiest way to demand that the field dies off on the spatial boundaries, that is
\begin{equation}\label{eqn:qftLecture4:420}
\lim_{\Abs{\Bx} \rightarrow \infty} \phi(\Bx) \rightarrow 0.
\end{equation}
The functional \( \phi(\Bx, t) \) that obeys the boundary condition as stated extremizes \( S[\phi] \).

Extremizing the action means that we seek \( \phi(\Bx, t) \)
\begin{equation}\label{eqn:qftLecture4:440}
\delta S[\phi] = 0 = S[\phi + \delta \phi] – S[\phi].
\end{equation}

How do we compute the variation?
\begin{equation}\label{eqn:qftLecture4:460}
\begin{aligned}
\delta S
&= \int d^d x \lr{ \LL(\phi + \delta \phi, \partial_\mu \phi + \partial_\mu \delta \phi) – \LL(\phi, \partial_\mu \phi) } \\
&= \int d^d x \lr{ \PD{\phi}{\LL} \delta \phi + \PD{(\partial_mu \phi)}{\LL} (\partial_\mu \delta \phi) } \\
&= \int d^d x \lr{ \PD{\phi}{\LL} \delta \phi
+ \partial_\mu \lr{ \PD{(\partial_mu \phi)}{\LL} \delta \phi}
– \lr{ \partial_\mu \PD{(\partial_mu \phi)}{\LL} } \delta \phi
} \\
&=
\int d^d x
\delta \phi
\lr{ \PD{\phi}{\LL}
– \partial_\mu \PD{(\partial_mu \phi)}{\LL} }
+ \int d^3 \sigma_\mu \lr{ \PD{(\partial_\mu \phi)}{\LL} \delta \phi }
\end{aligned}
\end{equation}

If we are explicit about the boundary term, we write it as
\begin{equation}\label{eqn:qftLecture4:480}
\int dt d^3 \Bx \partial_t \lr{ \PD{(\partial_t \phi)}{\LL} \delta \phi }
– \spacegrad \cdot \lr{ \PD{(\spacegrad \phi)}{\LL} \delta \phi }
=
\int d^3 \Bx \evalrange{ \PD{(\partial_t \phi)}{\LL} \delta \phi }{t = -T}{t = T}
– \int dt d^2 \BS \cdot \lr{ \PD{(\spacegrad \phi)}{\LL} \delta \phi }.
\end{equation}
but \( \delta \phi = 0 \) at \( t = \pm T \) and also at the spatial boundaries of the integration region.

This leaves
\begin{equation}\label{eqn:qftLecture4:500}
\delta S[\phi] = \int d^d x \delta \phi
\lr{ \PD{\phi}{\LL} – \partial_\mu \PD{(\partial_mu \phi)}{\LL} } = 0 \forall \delta \phi.
\end{equation}
That is

\begin{equation}\label{eqn:qftLecture4:540}
\boxed{
\PD{\phi}{\LL} – \partial_\mu \PD{(\partial_mu \phi)}{\LL} = 0.
}
\end{equation}

This are the Euler-Lagrange equations for a single scalar field.

Returning to our sample scalar Lagrangian
\begin{equation}\label{eqn:qftLecture4:560}
\LL = \inv{2} \partial_\mu \phi \partial^\mu \phi – \inv{2} m^2 \phi^2 – \frac{\lambda}{4} \phi^4.
\end{equation}
This example is related to the Ising model which has a \( \phi \rightarrow -\phi \) symmetry. Applying the Euler-Lagrange equations, we have
\begin{equation}\label{eqn:qftLecture4:580}
\PD{\phi}{\LL} = -m^2 \phi – \lambda \phi^3,
\end{equation}
and
\begin{equation}\label{eqn:qftLecture4:600}
\begin{aligned}
\PD{(\partial_\mu \phi)}{\LL}
&=
\PD{(\partial_\mu \phi)}{} \lr{
\inv{2} \partial_\nu \phi \partial^\nu \phi } \\
&=
\inv{2} \partial^\nu \phi
\PD{(\partial_\mu \phi)}{}
\partial_\nu \phi
+
\inv{2} \partial_\nu \phi
\PD{(\partial_\mu \phi)}{}
\partial_\alpha \phi g^{\nu\alpha} \\
&=
\inv{2} \partial^\mu \phi
+
\inv{2} \partial_\nu \phi g^{\nu\mu} \\
&=
\partial^\mu \phi
\end{aligned}
\end{equation}
so we have
\begin{equation}\label{eqn:qftLecture4:620}
\begin{aligned}
0
&=
\PD{\phi}{\LL} -\partial_\mu
\PD{(\partial_\mu \phi)}{\LL} \\
&=
-m^2 \phi – \lambda \phi^3 – \partial_\mu \partial^\mu \phi.
\end{aligned}
\end{equation}

For \( \lambda = 0 \), the free field theory limit, this is just
\begin{equation}\label{eqn:qftLecture4:640}
\partial_\mu \partial^\mu \phi + m^2 \phi = 0.
\end{equation}
Written out from the observer frame, this is
\begin{equation}\label{eqn:qftLecture4:660}
(\partial_t)^2 \phi – \spacegrad^2 \phi + m^2 \phi = 0.
\end{equation}

With a non-zero mass term
\begin{equation}\label{eqn:qftLecture4:680}
\lr{ \partial_t^2 – \spacegrad^2 + m^2 } \phi = 0,
\end{equation}
is called the Klein-Gordan equation.

If we also had \( m = 0 \) we’d have
\begin{equation}\label{eqn:qftLecture4:700}
\lr{ \partial_t^2 – \spacegrad^2 } \phi = 0,
\end{equation}
which is the wave equation (for a massless free field). This is also called the D’Alembert equation, which is familiar from electromagnetism where we have
\begin{equation}\label{eqn:qftLecture4:720}
\begin{aligned}
\lr{ \partial_t^2 – \spacegrad^2 } \BE &= 0 \\
\lr{ \partial_t^2 – \spacegrad^2 } \BB &= 0,
\end{aligned}
\end{equation}
in a source free region.

Canonical quantization.

\begin{equation}\label{eqn:qftLecture4:740}
\LL = \inv{2} \dot{q} – \frac{\omega^2}{2} q^2
\end{equation}
This has solution \(\ddot{q} = – \omega^2 q\).

Let
\begin{equation}\label{eqn:qftLecture4:760}
p = \PD{\dot{q}}{\LL} = \dot{q}
\end{equation}
\begin{equation}\label{eqn:qftLecture4:780}
H(p,q) = \evalbar{p \dot{q} – \LL}{\dot{q}(p, q)}
= p p – \inv{2} p^2 + \frac{\omega^2}{2} q^2 = \frac{p^2}{2} + \frac{\omega^2}{2} q^2
\end{equation}

In QM we quantize by mapping Poisson brackets to commutators.
\begin{equation}\label{eqn:qftLecture4:800}
\antisymmetric{\hatp}{\hat{q}} = -i
\end{equation}
One way to represent is to say that states are \( \Psi(\hat{q}) \), a wave function, \( \hat{q} \) acts by \( q \)
\begin{equation}\label{eqn:qftLecture4:820}
\hat{q} \Psi = q \Psi(q)
\end{equation}
With
\begin{equation}\label{eqn:qftLecture4:840}
\hatp = -i \PD{q}{},
\end{equation}
so
\begin{equation}\label{eqn:qftLecture4:860}
\antisymmetric{ -i \PD{q}{} } { q} = -i
\end{equation}

Let’s introduce an explicit space time split. We’ll write
\begin{equation}\label{eqn:qftLecture4:880}
L = \int d^3 x \lr{
\inv{2} (\partial_0 \phi(\Bx, t))^2 – \inv{2} \lr{ \spacegrad \phi(\Bx, t) }^2 – \frac{m^2}{2} \phi
},
\end{equation}
so that the action is
\begin{equation}\label{eqn:qftLecture4:900}
S = \int dt L.
\end{equation}
The dynamical variables are \( \phi(\Bx) \). We define
\begin{equation}\label{eqn:qftLecture4:920}
\begin{aligned}
\pi(\Bx, t) = \frac{\delta L}{\delta (\partial_0 \phi(\Bx, t))}
&=
\partial_0 \phi(\Bx, t) \\
&=
\dot{\phi}(\Bx, t),
\end{aligned}
\end{equation}
called the canonical momentum, or the momentum conjugate to \( \phi(\Bx, t) \). Why \( \delta \)? Has to do with an implicit Dirac function to eliminate the integral?

\begin{equation}\label{eqn:qftLecture4:940}
\begin{aligned}
H
&= \int d^3 x \evalbar{\lr{ \pi(\bar{\Bx}, t) \dot{\phi}(\bar{\Bx}, t) – L }}{\dot{\phi}(\bar{\Bx}, t) = \pi(x, t) } \\
&= \int d^3 x \lr{ (\pi(\Bx, t))^2 – \inv{2} (\pi(\Bx, t))^2 + \inv{2} (\spacegrad \phi)^2 + \frac{m}{2} \phi^2 },
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:qftLecture4:960}
H
= \int d^3 x \lr{ \inv{2} (\pi(\Bx, t))^2 + \inv{2} (\spacegrad \phi(\Bx, t))^2 + \frac{m}{2} (\phi(\Bx, t))^2 }
\end{equation}

In analogy to the momentum, position commutator in QM
\begin{equation}\label{eqn:qftLecture4:1000}
\antisymmetric{\hat{p}_i}{\hat{q}_j} = -i \delta_{ij},
\end{equation}
we “quantize” the scalar field theory by promoting \( \pi, \phi \) to operators and insisting that they also obey a commutator relationship
\begin{equation}\label{eqn:qftLecture4:980}
\antisymmetric{\pi(\Bx, t)}{\phi(\By, t)} = -i \delta^3(\Bx – \By).
\end{equation}

References

[1] Frank Wilczek. Fundamental constants. arXiv preprint arXiv:0708.4361, 2007. URL https://arxiv.org/abs/0708.4361.