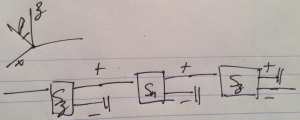[Click here for a PDF of this post with nicer formatting]
Question: Cascading Stern-Gerlach ([1] pr. 1.13)
Three Stern-Gerlach type measurements are performed, the first that prepares the state in a \( \ket{S_z ; + } \) state, the next in a \( \ket{ \BS \cdot \ncap ; + } \) state where \( \ncap = \cos\beta \zcap + \sin\beta \xcap \), and the last performing a \( S_z \) \( \Hbar/2 \) state measurement, as illustrated in fig. 1.
What is the intensity of the final \( s_z = -\Hbar/2 \) beam? What is the orientation for the second measuring apparatus to maximize the intensity of this beam?
Answer
The spin operator for the second apparatus is
\begin{equation}\label{eqn:sg:20}
\BS \cdot \ncap
= \frac{\Hbar}{2} \lr{ \sin\beta \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix} + \cos\beta \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} }
= \frac{\Hbar}{2}
\begin{bmatrix}
\cos\beta & \sin\beta \\
\sin\beta & -\cos\beta
\end{bmatrix}.
\end{equation}
The intensity of the final \( \ket{S_z ; -} \) beam is
\begin{equation}\label{eqn:sg:40}
P
= \Abs{ \braket{-}{\BS \cdot \ncap ; +} \braket{\BS \cdot \ncap ; +}{+} }^2,
\end{equation}
(i.e. the second apparatus applies a projection operator \( \ket{\BS \cdot \ncap ; +}\bra{\BS \cdot \ncap ; +} \) to the initial \( \ket{+} \) state, and then the \( \ket{-} \) states are selected out of that.
The \( \BS \cdot \ncap \) eigenket is found to be
\begin{equation}\label{eqn:sg:60}
\ket{\BS \cdot \ncap ; +} =
\begin{bmatrix}
\cos\frac{\beta}{2} \\
\sin\frac{\beta}{2} \\
\end{bmatrix},
\end{equation}
so
\begin{equation}\label{eqn:sg:80}
P
= \Abs{
\begin{bmatrix}
0 & 1
\end{bmatrix}
\begin{bmatrix}
\cos\frac{\beta}{2} \\
\sin\frac{\beta}{2} \\
\end{bmatrix}
\begin{bmatrix}
\cos\frac{\beta}{2} &
\sin\frac{\beta}{2} \\
\end{bmatrix}
\begin{bmatrix}
1 \\
0
\end{bmatrix}
}^2
=
\Abs{
\cos\frac{\beta}{2}
\sin\frac{\beta}{2}
}^2
=
\Abs{\inv{2} \sin\beta}^2
=
\inv{4} \sin^2\beta.
\end{equation}
This is maximized when \( \beta = \pi/2 \), or \( \ncap = \xcap \). At this angle the state leaving the second apparatus is
\begin{equation}\label{eqn:sg:100}
\begin{bmatrix}
\cos\frac{\beta}{2} \\
\sin\frac{\beta}{2} \\
\end{bmatrix}
\begin{bmatrix}
\cos\frac{\beta}{2} &
\sin\frac{\beta}{2} \\
\end{bmatrix}
\begin{bmatrix}
1 \\
0
\end{bmatrix}
=
\inv{2}
\begin{bmatrix}
1 \\ 1
\end{bmatrix}
\begin{bmatrix}
1 & 1
\end{bmatrix}
\begin{bmatrix}
1 \\ 0
\end{bmatrix}
=
\inv{2}
\begin{bmatrix}
1 \\ 1
\end{bmatrix}
=\inv{2} \ket{+} + \inv{2}\ket{-},
\end{equation}
so the state after filtering the \( \ket{-} \) states is \( \inv{2} \ket{-} \) with intensity (probability density) of \( 1/4 \) relative to a unit normalize input \( \ket{+} \) state to the \( \BS \cdot \ncap \) apparatus.
References
[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.