[Click here for a PDF of this post with nicer formatting]
DISCLAIMER: Very rough notes from class, with some additional side notes.
These are notes for the UofT course PHY2403H, Quantum Field Theory, taught by Prof. Erich Poppitz, fall 2018.
Review: “particle creation problem”.
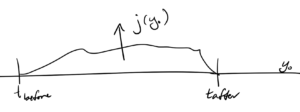
We imagined that we have a windowed source function \( j(y^0, \By) \), as sketched in fig. 1, which is acting as a forcing source for the non-homogeneous Klein-Gordon equation
\begin{equation}\label{eqn:qftLecture13:20}
\lr{ \partial_\mu \partial^\mu + m^2 } \phi = j
\end{equation}
Our solution was
\begin{equation}\label{eqn:qftLecture13:40}
\phi(x) = \phi(x_0) + i \int d^4 y D_R( x – y) j(y),
\end{equation}
where \( \phi(x_0) \) obeys the homogeneous equation, and
\begin{equation}\label{eqn:qftLecture13:60}
D_r(x – y) = \Theta(x^0 – y^0) \lr{ D(x – y) – D(y – x) },
\end{equation}
and \( D(x) = \int \frac{d^3 p}{(2\pi)^3 2 \omega_\Bp } \evalbar{ e^{-i p \cdot x} }{p^0 = \omega_\Bp} \) is the Weightmann function.
For \( x^0 > t_{\text{after}} \)
\begin{equation}\label{eqn:qftLecture13:80}
\phi(x)
=
\int \frac{d^3 p}{(2\pi)^3 \sqrt{ 2 \omega_\Bp }}
\evalbar{
\lr{ e^{-i p \cdot x} a_\Bp + e^{i p \cdot x } a_\Bp^\dagger }
}{
p^0 = \omega_\Bp
}
+ i
\int \frac{d^3 p}{(2\pi)^3 2 \omega_\Bp }
\evalbar{
\lr{ e^{-i p \cdot x} \tilde{j}(p) + e^{i p \cdot x} \tilde{j}(p_0, -\Bp) }
}{
p^0 = \omega_\Bp
}
\end{equation}
where we have used \( \tilde{j}^\conj(p_0, \Bp) = \tilde{j}(p_0, -\Bp) \). This gives
\begin{equation}\label{eqn:qftLecture13:100}
\phi(x) =
\int \frac{d^3 p}{(2\pi)^3 \sqrt{ 2 \omega_\Bp } }
\evalbar{
\lr{
e^{-i p \cdot x}
\lr{ a_\Bp + i \frac{\tilde{j}(p)}{\sqrt{2 \omega_\Bp}} }
+ e^{i p \cdot x }
\lr{ a_\Bp^\dagger – i \frac{\tilde{j}^\conj(p)}{\sqrt{2 \omega_\Bp}} }
}
}{
p^0 = \omega_\Bp
}
\end{equation}
It was left as an exercise to show that given
\begin{equation}\label{eqn:qftLecture13:120}
H = \int d^3 p \lr{ \inv{2} \pi^2 + \inv{2} \lr{ \spacegrad \phi}^2 + \frac{m^2}{2} \phi^2 },
\end{equation}
we obtain
\begin{equation}\label{eqn:qftLecture13:140}
H_{\text{after}} =
\int d^3 x \omega_\Bp
\lr{ a_\Bp^\dagger – i \frac{\tilde{j}^\conj(p)}{\sqrt{2 \omega_\Bp}} }
\lr{ a_\Bp + i \frac{\tilde{j}(p)}{\sqrt{2 \omega_\Bp}} }
\end{equation}
System in ground state
\begin{equation}\label{eqn:qftLecture13:160}
\bra{0} \hatH_{\text{before}} \ket{0} = \expectation{E}_{\text{before}} = 0.
\end{equation}
\begin{equation}\label{eqn:qftLecture13:180}
\begin{aligned}
\bra{0} \hatH_{\text{after}} \ket{0} = \expectation{E}_{\text{after}}
&=
\int d^3 x \omega_\Bp
\frac{ \tilde{j}^\conj(p) \tilde{j}(p)}{2 \omega_\Bp} \\
&=
\inv{2} \int d^3 x
\Abs{j(p)}^2.
\end{aligned}
\end{equation}
We can identify
\begin{equation}\label{eqn:qftLecture13:200}
N(\Bp) =
\frac{\Abs{j(p)}^2}{2 \omega_\Bp},
\end{equation}
as the number density of particles with momentum \( \Bp \).
Digression: coherent states.
Defintion: Coherent state.
A coherent state is an eigenstate of the destruction operator
\begin{equation*}
a \ket{\alpha} = \alpha \ket{\alpha}.
\end{equation*}
For the SHO, if we solve for such a coherent state, we find
\begin{equation}\label{eqn:qftLecture13:240}
\ket{\alpha} = \text{constant} \times \sum_{n = 0}^\infty \frac{\alpha^n}{n!} \lr{ a^\dagger }^n \ket{0}.
\end{equation}
If we assume the existence of a coherent state
\begin{equation}\label{eqn:qftLecture13:260}
a_\Bp \ket{
\frac{j(p)}{\sqrt{2 \omega_\Bp}}
}
=
\frac{j(p)}{\sqrt{2 \omega_\Bp}}
\ket{
\frac{j(p)}{\sqrt{2 \omega_\Bp}}
},
\end{equation}
then the expectation value of the number operator with respect to this state is the number density identified in \ref{eqn:qftLecture13:200}
\begin{equation}\label{eqn:qftLecture13:1200}
\bra{
\frac{j(p)}{\sqrt{2 \omega_\Bp}}
}
a_\Bp^\dagger a_\Bp
\ket{
\frac{j(p)}{\sqrt{2 \omega_\Bp}}
} = \frac{\Abs{j(p)}^2}{2 \omega_\Bp} = N(\Bp).
\end{equation}
Feynman’s Green’s function
\begin{equation}\label{eqn:qftLecture13:280}
\begin{aligned}
D_F(x)
&=
\Theta(x^0) D(x) +
\Theta(-x^0) D(-x) \\
&=
\Theta(x^0) \bra{0} \phi(x) \phi(0) \ket{0}
+\Theta(x^0) \bra{0} \phi(-x) \phi(0) \ket{0}
\end{aligned}
\end{equation}
Utilizing a translation operation \( U(a) = e^{i a_\mu P^\mu } \), where \( U(a) \phi(y) U^\dagger(a) = \phi(y + a) \), this second operation can be written as
\begin{equation}\label{eqn:qftLecture13:300}
\begin{aligned}
\bra{0} \phi(-x) \phi(0) \ket{0}
&=
\bra{0} U^\dagger(a) U(a) \phi(-x) U^\dagger(a) U(a) \phi(0) U^\dagger(a) U(a) \ket{0} \\
&=
\bra{0} U(a) \phi(-x) U^\dagger(a) U(a) \phi(0) U^\dagger(a) \ket{0} \\
&=
\bra{0} \phi(-x + a) \phi(a) \ket{0},
\end{aligned}
\end{equation}
In particular, with \( a = x \)
\begin{equation}\label{eqn:qftLecture13:320}
\bra{0} \phi(-x) \phi(0) \ket{0}
=
\bra{0} \phi(0) \phi(x) \ket{0},
\end{equation}
so the Feynman’s Green function can be written
\begin{equation}\label{eqn:qftLecture13:340}
D_F(x) =
\Theta(x^0) \bra{0} \phi(x) \phi(0) \ket{0}
+\Theta(x^0) \bra{0} \phi(x) \phi(x) \ket{0}
=
\bra{0}
\lr{
\Theta(x^0)
\phi(x) \phi(0)
+
\Theta(-x^0)
\phi(0) \phi(x)
}
\ket{0}.
\end{equation}
We define
Definition: Time ordered product.
The time ordered product of two operators is defined as
\begin{equation*}
T(\phi(x) \phi(y)) =
\left\{
\begin{array}{l l}
\phi(x)\phi(y) & \quad \mbox{\( x^0 > y^0 \)} \\
\phi(y)\phi(x) & \quad \mbox{\( x^0 < y^0 \)} \\
\end{array}
\right.,
\end{equation*}
or
\begin{equation*}
T(\phi(x) \phi(y)) =
\phi(x)\phi(y) \Theta(x^0 – y^0)
+
\phi(y)\phi(x) \Theta(y^0 – x^0).
\end{equation*}
Using this helpful construct, the Feynman’s Green function can now be written in a very simple fashion
\begin{equation}\label{eqn:qftLecture13:380}
\boxed{
D_F(x) = \bra{0} T(\phi(x) \phi(0)) \ket{0}.
}
\end{equation}
Remark:
Recall that the four dimensional form of the Green’s function was
\begin{equation}\label{eqn:qftLecture13:400}
D_F = i \int \frac{d^4 p}{(2 \pi)^4} e^{-i p \cdot x} \inv{ p^2 – m^2 }.
\end{equation}
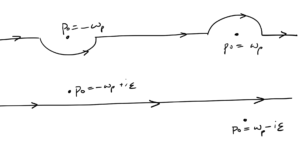
For the Feynman case, the contour that we were taking around the poles can also be accomplished by shifting the poles strategically, as sketched in fig. 2.
This shift can be expressed explicit algebraically by introducing an offset
\begin{equation}\label{eqn:qftLecture13:420}
D_F = i \int \frac{d^4 p}{(2 \pi)^4} e^{-i p \cdot x} \inv{ p^2 – m^2 + i \epsilon }
\end{equation}
which puts the poles at
\begin{equation}\label{eqn:qftLecture13:440}
\begin{aligned}
p^0
&= \pm \sqrt{ \omega_\Bp – i \epsilon } \\
&= \pm \omega_\Bp \lr{ 1 – \frac{i \epsilon}{\omega_\Bp^2} }^{1/2} \\
&= \pm \omega_\Bp \lr{ 1 – \inv{2} \frac{i \epsilon}{\omega_\Bp^2} } \\
&=
\left\{
\begin{array}{l}
+\omega_\Bp – \inv{2} i \frac{\epsilon}{\omega_\Bp} \\
-\omega_\Bp + \inv{2} i \frac{\epsilon}{\omega_\Bp} \\
\end{array}
\right.
\end{aligned}
\end{equation}
Interacting field theory: perturbation theory in QFT.
We perturb the Hamiltonian
\begin{equation}\label{eqn:qftLecture13:500}
H = H_0 + H_{\text{int}}
\end{equation}
where \( H_0 \) is the free Hamiltonian and \( H_{\text{int}} \) is the interaction term (the perturbation).
Example:
\begin{equation}\label{eqn:qftLecture13:460}
\begin{aligned}
H_0 &= SHO = \frac{p^2}{2} + \frac{\omega^2 q^2}{2} \\
H_{\text{int}} &= \lambda q^4,
\end{aligned}
\end{equation}
i.e. the anharmonic oscillator.
In QFT
\begin{equation}\label{eqn:qftLecture13:480}
\begin{aligned}
H_0 &=
\int d^3 x \lr{ \inv{2} \pi^2 + \inv{2} \lr{ \spacegrad \phi}^2 + \frac{m^2}{2} \phi^2 } \\
H_{\text{int}} &=
\lambda \int d^3 x \phi^4.
\end{aligned}
\end{equation}
We will expand the interaction in small \( \lambda \). Perturbation theory is the expansion in a small dimensionless coupling constant, such as
- \( \lambda \) in \( \lambda \phi^4 \) theory,
- \( \alpha = e^2/4 \pi \sim \inv{137} \) in QED, and
- \( \alpha_s \) in QCD.
Perturbation theory, interaction representation and Dyson formula
\begin{equation}\label{eqn:qftLecture13:520}
H = H_0 + H_{\text{int}}
\end{equation}
Example interaction
\begin{equation}\label{eqn:qftLecture13:540}
H_{\text{int}} = \lambda \int d^3 x \phi^4
\end{equation}
We know all there is to know about \( H_0 \) (decoupled SHOs, …)
\begin{equation}\label{eqn:qftLecture13:560}
H_0 \ket{0} = \ket{0} E^0_{\text{vac}}
\end{equation}
where \( E^0_{\text{vac}} = 0 \). Assume
\begin{equation}\label{eqn:qftLecture13:580}
\lr{ H_0 + H_{\text{int}} } \ket{\Omega} = \ket{\Omega} E_{\text{vac}},
\end{equation}
where the ground state energy of the perturbed system is zero when \( \lambda = 0 \). That is \( E_{\text{vac}}(\lambda = 0 ) = 0 \).
So for
\begin{equation}\label{eqn:qftLecture13:600}
\evalbar{\phi(x) }{x^0 = t_0, \text{some fixed value}}
=
\int \frac{d^3}{(2 \pi)^3 \sqrt{ 2 \omega_\Bp } }
\evalbar{
\lr{
e^{-i p \cdot x} a_\Bp
+ e^{i p \cdot x} a_\Bp^\dagger }
}
{
p^0 = \omega_\Bp
}.
\end{equation}
Let’s call \( \phi(\Bx, t_0) \) the free Schr\”{o}dinger operator, where
\( \phi(\Bx, t_0) \) is evaluated at a fixed value of \( t_0 \). At such a point, the Schr\”{o}dinger and Heisenberg pictures coincide.
\begin{equation}\label{eqn:qftLecture13:620}
\antisymmetric{\phi(\Bx, t_0)}{\pi(\By, t_0)} = i \delta^3(\Bx – \By).
\end{equation}
Normally (QM) one defines the Heisenberg operator as
\begin{equation}\label{eqn:qftLecture13:640}
O_H = e^{i H(t – t_0)} O_S e^{-i H(t – t_0)},
\end{equation}
where \( O_H \) depends on time, and \( O_S \) is defined at a fixed time \( t_0 \), usually 0.
From \ref{eqn:qftLecture13:640} we find
\begin{equation}\label{eqn:qftLecture13:660}
\ddt{O_H} = i \antisymmetric{H}{O_H}.
\end{equation}
The equivalent of \ref{eqn:qftLecture13:640} in QFT is very complicated. We’d like to develop an intermediate picture.
We will define an intermediate picture, called the “interaction representation”, which is equivalent to the Heisenberg picture with respect to \( H_0 \).
Definition: Intermediate picture operator.
\begin{equation*}
\phi_I(t, \Bx) =
e^{i H_0(t – t_0) }
\phi(t_0, \Bx)
e^{-i H_0(t – t_0) }.
\end{equation*}
This is familiar, and is the Heisenberg picture operator that we had in free QFT
\begin{equation}\label{eqn:qftLecture13:700}
\phi_I(t, \Bx) =
\int \frac{d^3}{(2 \pi)^3 \sqrt{ 2 \omega_\Bp } }
\evalbar{
\lr{
e^{-i p \cdot x} a_\Bp
+ e^{i p \cdot x} a_\Bp^\dagger }
}
{
p^0 = \omega_\Bp
},
\end{equation}
where \( x_0 = t \).
The Heisenberg picture operator is
\begin{equation}\label{eqn:qftLecture13:720}
\begin{aligned}
\phi_H(t, \Bx)
&=
\phi(t, \Bx) \\
&=
e^{i H(t – t_0) }
e^{-i H_0(t – t_0) }
\lr{
e^{i H_0(t – t_0) }
\phi_S(t_0, \Bx)
e^{-i H_0(t – t_0) }
}
e^{i H_0(t – t_0) }
e^{-i H(t – t_0) } \\
&=
e^{i H(t – t_0) }
e^{-i H_0(t – t_0) }
\phi_I(t, \Bx)
e^{-i H_0(t – t_0) }
e^{i H(t – t_0) }
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:qftLecture13:760}
\phi_H(t, \Bx)
=
U^\dagger(t, t_0)
\phi_I(t_0, \Bx)
U(t, t_0),
\end{equation}
where
\begin{equation}\label{eqn:qftLecture13:740}
U(t, t_0) =
e^{i H_0(t – t_0) }
e^{-i H(t – t_0) }.
\end{equation}
We want to apply perturbation techniques to find \( U(t, t_0) \) which is complicated.
\begin{equation}\label{eqn:qftLecture13:780}
\begin{aligned}
i \PD{t}{} U(t, t_0)
&=
i e^{i H_0(t – t_0) } i H_0
e^{-i H(t – t_0) }
+
i e^{i H_0(t – t_0) }
e^{-i H(t – t_0) } (-i H) \\
&=
e^{i H_0(t – t_0) }
\lr{ -H_0 + H }
e^{-i H(t – t_0) } \\
&=
e^{i H_0(t – t_0) }
H_{\text{int}}
e^{-i H_0(t – t_0) }
e^{i H_0(t – t_0) }
e^{-i H(t – t_0) }
\end{aligned}
\end{equation}
so we have
\begin{equation}\label{eqn:qftLecture13:800}
\boxed{
i \PD{t}{} U(t, t_0)
=
H_{\text{int}, I}(t) U(t, t_0).
}
\end{equation}
For the (Schr\”{o}dinger) interaction \( H_{\text{int}} = \
\lambda \int d^3 x \phi^4(\Bx, t_0) \), what we really mean by
\( H_{\text{int}, I}(t) \) is
\begin{equation}\label{eqn:qftLecture13:820}
H_{\text{int}, I}(t) = \lambda \int d^3 x \phi_I^4(\Bx, t).
\end{equation}
It will be more convenient to remove the explicit \( \lambda \) factor from the interaction Hamiltonian, and write instead
\begin{equation}\label{eqn:qftLecture13:880}
H_{\text{int}, I}(t) = \int d^3 x \phi_I^4(\Bx, t),
\end{equation}
so the equation to solve is
\begin{equation}\label{eqn:qftLecture13:1220}
i \PD{t}{} U(t, t_0)
=
\lambda H_{\text{int}, I}(t) U(t, t_0).
\end{equation}
We assume that
\begin{equation}\label{eqn:qftLecture13:900}
U(t, t_0)
=
U_0(t, t_0)
+ \lambda U_1(t, t_0)
+ \lambda^2 U_2(t, t_0)
+ \cdots
+ \lambda^n U_n(t, t_0)
\end{equation}
Plugging into \ref{eqn:qftLecture13:880} we have
\begin{equation}\label{eqn:qftLecture13:1160}
\begin{aligned}
i &\lambda^0 \PD{t}{}U_0(t, t_0)
+ i \lambda^1 \PD{t}{}U_1(t, t_0)
+ i \lambda^2 \PD{t}{}U_2(t, t_0)
+ \cdots
+ i \lambda^n \PD{t}{}U_n(t, t_0) \\
&=
\lambda H_{\text{int}, I}(t)
\lr{
1
+ \lambda U_1(t, t_0)
+ \lambda^2 U_2(t, t_0)
+ \cdots
+ \lambda^n U_n(t, t_0)
},
\end{aligned},
\end{equation}
so
equating equal powers of \( \lambda \) on each side gives a recurrence relation for each \( U_k, k > 0 \)
\begin{equation}\label{eqn:qftLecture13:1180}
\PD{t}{}U_k(t, t_0) = -i H_{\text{int}, I}(t) U_{k-1}(t, t_0).
\end{equation}
Let’s consider each power in turn.
\(O(\lambda^0)\):
Solving \ref{eqn:qftLecture13:800} to \( O(\lambda^0) \) gives
\begin{equation}\label{eqn:qftLecture13:840}
i \PD{t}{} U_0(t, t_0) = 0,
\end{equation}
or
\begin{equation}\label{eqn:qftLecture13:860}
U(t, t_0) = 1 + O(\lambda).
\end{equation}
\(O(\lambda^1)\):
\begin{equation}\label{eqn:qftLecture13:940}
\PD{t}{U_1(t, t_0)} = -i H_{\text{int}, I}(t),
\end{equation}
which has solution
\begin{equation}\label{eqn:qftLecture13:960}
U_1(t, t_0) = -i \int_{t_0}^t H_{\text{int}, I}(t’) dt’.
\end{equation}
\(O(\lambda^2)\):
\begin{equation}\label{eqn:qftLecture13:1000}
\begin{aligned}
\PD{t}{U_2(t, t_0)}
&= -i H_{\text{int}, I}(t) U_1(t, t_0) \\
&= (-i)^2 H_{\text{int}, I}(t)
\int_{t_0}^t H_{\text{int}, I}(t’) dt’,
\end{aligned}
\end{equation}
which has solution
\begin{equation}\label{eqn:qftLecture13:1020}
\begin{aligned}
U_2(t, t_0)
&= (-i )^2
\int_{t_0}^t H_{\text{int}, I}(t”) dt”
\int_{t_0}^{t”} H_{\text{int}, I}(t’) dt’ \\
&= (-i )^2
\int_{t_0}^t dt”
\int_{t_0}^{t”}
dt’
H_{\text{int}, I}(t”)
H_{\text{int}, I}(t’).
\end{aligned}
\end{equation}
\(O(\lambda^3)\):
\begin{equation}\label{eqn:qftLecture13:1060}
\PD{t}{U_3(t, t_0)}
=
-i
H_{\text{int}, I}(t) U_2(t, t_0)
\end{equation}
so
\begin{equation}\label{eqn:qftLecture13:1240}
\begin{aligned}
U_3(t, t_0)
&=
-i
\int_{t_0}^t dt”’
H_{\text{int}, I}(t”’) U_2(t”’, t_0) \\
&=
(-i )^3
\int_{t_0}^t dt”’
H_{\text{int}, I}(t”’)
\int_{t_0}^{t”’} dt”
\int_{t_0}^{t”}
dt’
H_{\text{int}, I}(t”)
H_{\text{int}, I}(t’) \\
&=
(-i)^3
\int_{t_0}^t dt”’
\int_{t_0}^{t”’} dt”
\int_{t_0}^{t”} dt’
H_{\text{int}, I}(t”’)
H_{\text{int}, I}(t”)
H_{\text{int}, I}(t’)
\end{aligned}
\end{equation}
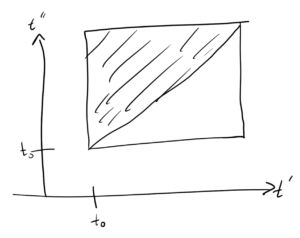
Simplifying the integration region.
For the two fold integral, the integration range is the upper triangular region sketched in fig. 3.
Claim:
We can integrate over the entire square, and divide by two, provided we keep the time ordering
\begin{equation}\label{eqn:qftLecture13:1040}
U_2(t, t_0)
= \frac{(-i )^2}{2}
\int_{t_0}^t dt”
\int_{t_0}^{t”}
dt’
T(H_{\text{int}, I}(t”) H_{\text{int}, I}(t’) )
\end{equation}
Demonstration:
\begin{equation}\label{eqn:qftLecture13:1100}
\begin{aligned}
\frac{(-i)^2}{2}
&\int_{t_0}^t dt”
\int_{t_0}^t dt’
T( H_I(t”) H_I(t’) ) \\
&=
\frac{(-i)^2}{2}
\int_{t_0}^t dt”
\int_{t_0}^t dt’
\Theta(t”- t’)
H_I(t”) H_I(t’)
+
\frac{(-i)^2}{2}
\int_{t_0}^t dt”
\int_{t_0}^t dt’
\Theta(t’- t”)
H_I(t’) H_I(t”),
\end{aligned}
\end{equation}
but the \( \Theta(t” – t’) \) function is non-zero only for \( t” – t’ > 0 \), or \( t’ < t” \), and the \( \Theta(t’ – t”) \) function is non-zero only for \( t’ – t” > 0 \), or \( t” < t’ \), so we can adjust the integration ranges for
\begin{equation}\label{eqn:qftLecture13:1260}
\begin{aligned}
\frac{(-i)^2}{2}
&\int_{t_0}^t dt”
\int_{t_0}^t dt’
T( H_I(t”) H_I(t’) ) \\
&=
\frac{(-i)^2}{2}
\int_{t_0}^t dt”
\int_{t_0}^{t”} dt’
H_I(t”) H_I(t’)
+
\frac{(-i)^2}{2}
\int_{t_0}^{t’} dt”
\int_{t_0}^t dt’
H_I(t’) H_I(t”) \\
&=
\frac{(-i)^2}{2}
\int_{t_0}^t dt”
\int_{t_0}^{t”} dt’
H_I(t”) H_I(t’)
+
\frac{(-i)^2}{2}
\int_{t_0}^t dt”
\int_{t_0}^{t”} dt’
H_I(t”) H_I(t’) \\
&=
U_2(t, t_0),
\end{aligned}
\end{equation}
where we swapped integration variables in second integral. We can clearly do the same thing for the higher order repeated integrals, but instead of a \(1/2 = 1/2!\) adjustment for the number of orderings, we will require a \( 1/n! \) adjustment for an \( n \)-fold integral.
Summary:
\begin{equation}\label{eqn:qftLecture13:1120}
\begin{aligned}
U_0 &= 1 \\
U_1 &= -i \int_{t_0}^t dt_1 H_I(t_1) \\
U_2 &= \frac{(-i)^2}{2}
\int_{t_0}^t dt_1
\int_{t_0}^t dt_2
T( H_I(t_1)
H_I(t_2) ) \\
U_3 &= \frac{(-i)^3}{3!}
\int_{t_0}^t dt_1
\int_{t_0}^t dt_2
\int_{t_0}^t dt_3
T( H_I(t_1)
H_I(t_2)
H_I(t_3)
) \\
U_n &= \frac{(-i)^n}{n!}
\int_{t_0}^t dt_1
\int_{t_0}^t dt_2
\int_{t_0}^t dt_3
\cdots
\int_{t_0}^t dt_n
T( H_I(t_1)
H_I(t_2)
\cdots
H_I(t_n)
) \\
\end{aligned}
\end{equation}
Summing we find
\begin{equation}\label{eqn:qftLecture13:1140}
\begin{aligned}
U(t, t_0)
&= T \exp\lr{-i
\int_{t_0}^t dt_1 H_I(t’)
} \\
&=
\sum_{n = 0}^\infty
\frac{(-i)^n}{n!} \int_{t_0}^t dt_1 \cdots dt_n T( H_I(t_1) \cdots H_I(t_n) ).
\end{aligned}
\end{equation}
This is called Dyson’s formula.
Next time.
Our goal is to compute: \( \bra{\Omega} T(\phi(x_1) \cdots \phi(x_n)) \ket{\Omega} \).