Month: October 2014

ECE1254H Modeling of Multiphysics Systems. Lecture 7: Sparse factorization and iterative methods. Taught by Prof. Piero Triverio

October 21, 2014 ece1254 , , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

Fill ins

The problem of fill ins in LU computations arise in locations where rows and columns cross over zero positions.

Rows and columns can be permuted to deal with these. Here is an ad-hoc permutation of rows and columns that will result in less fill ins.

\begin{equation}\label{eqn:multiphysicsL7:180}
\begin{aligned}
&
\begin{bmatrix}
a & b & c & 0 \\
d & e & 0 & 0 \\
0 & f & g & 0 \\
0 & h & 0 & i \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
x_3 \\
x_4
\end{bmatrix}
=
\begin{bmatrix}
b_1 \\
b_2 \\
b_3 \\
b_4
\end{bmatrix} \\
\Rightarrow &
\begin{bmatrix}
a & c & 0 & b \\
d & 0 & 0 & e \\
0 & g & 0 & f \\
0 & 0 & i & h \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_4 \\
x_3 \\
x_2 \\
\end{bmatrix}
=
\begin{bmatrix}
b_1 \\
b_2 \\
b_3 \\
b_4 \\
\end{bmatrix} \\
\Rightarrow &
\begin{bmatrix}
0 & a & c & b \\
0 & d & 0 & e \\
0 & 0 & g & f \\
i & 0 & 0 & h \\
\end{bmatrix}
\begin{bmatrix}
x_3 \\
x_4 \\
x_1 \\
x_2 \\
\end{bmatrix}
=
\begin{bmatrix}
b_1 \\
b_2 \\
b_3 \\
b_4 \\
\end{bmatrix} \\
\Rightarrow &
\begin{bmatrix}
i & 0 & 0 & h \\
0 & a & c & b \\
0 & d & 0 & e \\
0 & 0 & g & f \\
\end{bmatrix}
\begin{bmatrix}
x_3 \\
x_4 \\
x_1 \\
x_2 \\
\end{bmatrix}
=
\begin{bmatrix}
b_4 \\
b_1 \\
b_2 \\
b_3 \\
\end{bmatrix} \\
\Rightarrow &
\begin{bmatrix}
i & 0 & 0 & h \\
0 & c & a & b \\
0 & 0 & d & e \\
0 & g & 0 & f \\
\end{bmatrix}
\begin{bmatrix}
x_3 \\
x_1 \\
x_4 \\
x_2 \\
\end{bmatrix}
=
\begin{bmatrix}
b_4 \\
b_1 \\
b_2 \\
b_3 \\
\end{bmatrix} \\
\end{aligned}
\end{equation}

Markowitz product

To facilitate such permutations the Markowitz product that estimates the amount of fill in required.

Definition Markowitz product

\begin{equation*}
\begin{aligned}
\text{Markowitz product} =
&\lr{\text{Non zeros in unfactored part of Row -1}} \times \\
&\lr{\text{Non zeros in unfactored part of Col -1}}
\end{aligned}
\end{equation*}

In [1] it is stated “A still simpler alternative, which seems adequate generally, is to choose the pivot which minimizes the number of coefficients modified at each step (excluding those which are eliminated at the particular step). This is equivalent to choosing the non-zero element with minimum \( (\rho_i – 1 )(\sigma_j -1) \).”

Note that this product is applied only to \( i j \) positions that are
non-zero, something not explicitly mentioned in the slides, nor in other
locations like [2]

Example: Markowitz product

For this matrix
\begin{equation}\label{eqn:multiphysicsL7:220}
\begin{bmatrix}
a & b & c & 0 \\
d & e & 0 & 0 \\
0 & f & g & 0 \\
0 & h & 0 & i \\
\end{bmatrix},
\end{equation}

the Markowitz products are

\begin{equation}\label{eqn:multiphysicsL7:280}
\begin{bmatrix}
1 & 6 & 2 & \\
1 & 3 & & \\
& 3 & 1 & \\
& 3 & & 0 \\
\end{bmatrix}.
\end{equation}

Markowitz reordering

The Markowitz Reordering procedure (copied directly from the slides) is

  • For i = 1 to n
  • Find diagonal \( j >= i \) with min Markowitz product
  • Swap rows \( j \leftrightarrow i \) and columns \( j \leftrightarrow i \)
  • Factor the new row \( i \) and update Markowitz products

Example: Markowitz reordering

Looking at the Markowitz products \ref{eqn:multiphysicsL7:280} a swap of rows and columns \( 1, 4 \) gives the modified matrix

\begin{equation}\label{eqn:multiphysicsL7:300}
\begin{bmatrix}
i & 0 & h & 0 \\
0 & d & e & 0 \\
0 & 0 & f & g \\
0 & a & b & c \\
\end{bmatrix}
\end{equation}

In this case, this reordering has completely avoided any requirement to do any actual Gaussian operations for this first stage reduction.

Presuming that the Markowitz products for the remaining 3×3 submatrix are only computed from that submatrix, the new products are
\begin{equation}\label{eqn:multiphysicsL7:320}
\begin{bmatrix}
& & & \\
& 1 & 2 & \\
& & 2 & 1 \\
& 2 & 4 & 2 \\
\end{bmatrix}.
\end{equation}

We have a minimal product in the pivot position, which happens to already lie on the diagonal. Note that it is not necessarily the best for numerical stability. It appears the off diagonal Markowitz products are not really of interest since the reordering algorithm swaps both rows and columns.

Graph representation

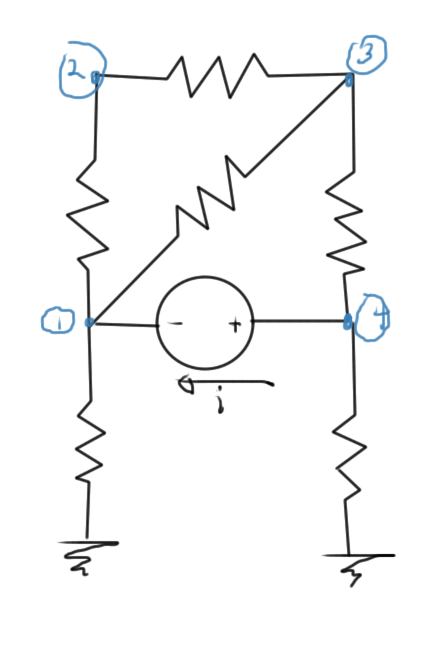
It is possible to interpret the Markowitz products on the diagonal as connectivity of a graph that represents the interconnections of the nodes. Consider the circuit of fig. 2 as an example

lecture7Fig2

fig 2. Simple circuit

 

The system equations for this circuit is of the form
\begin{equation}\label{eqn:multiphysicsL7:340}
\begin{bmatrix}
x & x & x & 0 & 1 \\
x & x & x & 0 & 0 \\
x & x & x & x & 0 \\
0 & 0 & x & x & -1 \\
-1 & 0 & 0 & 1 & 0 \\
\end{bmatrix}
\begin{bmatrix}
V_1 \\
V_2 \\
V_3 \\
V_4 \\
i \\
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0 \\
0 \\
x \\
\end{bmatrix}.
\end{equation}

The Markowitz products along the diagonal are
\begin{equation}\label{eqn:multiphysicsL7:360}
\begin{aligned}
M_{11} &= 9 \\
M_{22} &= 4 \\
M_{33} &= 9 \\
M_{44} &= 4 \\
M_{55} &= 4 \\
\end{aligned}
\end{equation}

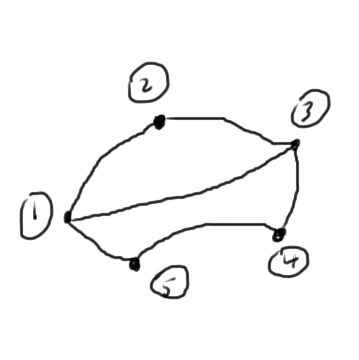
Compare these to the number of interconnections of the graph fig. 3 of the nodes in this circuit. We see that these are the squares of the number of the node interconnects in each case.

 

lecture7Fig3

fig. 3. Graph representation

Here a 5th node was introduced for the current \( i \) between nodes \( 4 \) and \( 1 \). Observe that the Markowitz product of this node was counted as the number of non-zero values excluding the \( 5,5 \) matrix position. However, that doesn’t matter too much since a Markowitz swap of row/column 1 with row/column 5 would put a zero in the \( 1,1 \) position of the matrix, which is not desirable. We have to restrict the permutations of zero diagonal positions to pivots for numerical stability, or use a more advanced zero fill avoidance algorithm.

The minimum diagonal Markowitz products are in positions 2 or 4, with respective Markowitz reorderings of the form

\begin{equation}\label{eqn:multiphysicsL7:380}
\begin{bmatrix}
x & x & x & 0 & 0 \\
x & x & x & 0 & 1 \\
x & x & x & x & 0 \\
0 & 0 & x & x & -1 \\
0 & -1 & 0 & 1 & 0 \\
\end{bmatrix}
\begin{bmatrix}
V_2 \\
V_1 \\
V_3 \\
V_4 \\
i \\
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0 \\
0 \\
x \\
\end{bmatrix},
\end{equation}

and
\begin{equation}\label{eqn:multiphysicsL7:400}
\begin{bmatrix}
x & 0 & 0 & x & -1 \\
0 & x & x & x & 1 \\
0 & x & x & x & 0 \\
x & x & x & x & 0 \\
1 & -1 & 0 & 0 & 0 \\
\end{bmatrix}
\begin{bmatrix}
V_4 \\
V_1 \\
V_2 \\
V_3 \\
i \\
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0 \\
0 \\
x \\
\end{bmatrix}.
\end{equation}

The original system had 7 zeros that could potentially be filled in the remaining \( 4 \times 4 \) submatrix. After a first round of Gaussian elimination, our system matrices have the respective forms

\begin{equation}\label{eqn:multiphysicsL7:420}
\begin{bmatrix}
x & x & x & 0 & 0 \\
0 & x & x & 0 & 1 \\
0 & x & x & x & 0 \\
0 & 0 & x & x & -1 \\
0 & -1 & 0 & 1 & 0 \\
\end{bmatrix}
\end{equation}
\begin{equation}\label{eqn:multiphysicsL7:440}
\begin{bmatrix}
x & 0 & 0 & x & -1 \\
0 & x & x & x & 1 \\
0 & x & x & x & 0 \\
0 & x & x & x & 0 \\
0 & -1 & 0 & x & x \\
\end{bmatrix}
\end{equation}

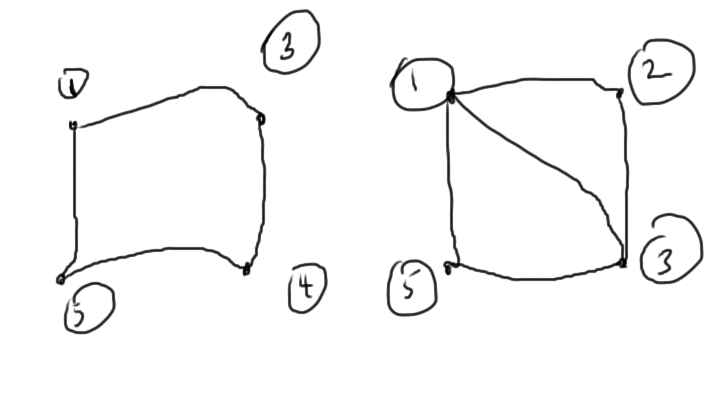
The remaining \( 4 \times 4 \) submatrices have interconnect graphs sketched in fig. 4.

 

lecture7Fig4

fig. 4. Graphs after one round of Gaussian elimination

From a graph point of view, we want to delete the most connected nodes. This can be driven by the Markowitz products along the diagonal or directly with graph methods.

Summary of factorization costs

LU (dense)

  • cost: \( O(n^3) \)
  • cost depends only on size

LU (sparse)

  • cost: Diagonal and tridiagonal are \( O(n) \), but we can have up to \( O(n^3) \) depending on sparsity and the method of dealing with the sparsity.
  • cost depends on size and sparsity

Computation can be affordable up to a few million elements.

Iterative methods

Can be cheap if done right. Convergence requires careful preconditioning.

Iterative methods

Suppose that we have an initial guess \( \Bx_0 \). Iterative methods are generally of the form

DO
\(\Br = \Bb – M \Bx_i\)
UNTIL \(\Norm{\Br} < \epsilon \)

The difference \( \Br \) is called the residual. For as long as it is bigger than desired, continue improving the estimate \( \Bx_i \).

The matrix vector product \( M \Bx_i \), if dense, is of \( O(n^2) \). Suppose, for example, that we can perform the iteration in ten iterations. If the matrix is dense, we can have \( 10 \, O(n^2) \) performance. If sparse, this can be worse than just direct computation.

Gradient method

This is a method for iterative solution of the equation \( M \Bx = \Bb \).

This requires symmetric positive definite matrix \( M = M^\T \), with \( M > 0 \).

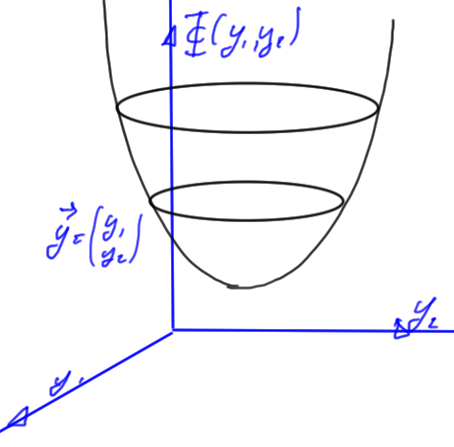
We introduce an energy function

\begin{equation}\label{eqn:multiphysicsL7:60}
\Psi(\By) \equiv \inv{2} \By^\T M \By – \By^\T \Bb
\end{equation}

For a two variable system this is illustrated in fig. 1.

 

lecture7Fig1

fig. 1. Positive definite energy function

Theorem: Energy function minimum

The energy function \ref{eqn:multiphysicsL7:60} has a minimum at

\begin{equation}\label{eqn:multiphysicsL7:80}
\By = M^{-1} \Bb = \Bx.
\end{equation}

To prove this, consider the coordinate representation

\begin{equation}\label{eqn:multiphysicsL7:480}
\Psi = \inv{2} y_a M_{ab} y_b – y_b b_b,
\end{equation}

for which the derivatives are
\begin{equation}\label{eqn:multiphysicsL7:500}
\PD{y_i}{\Psi} =
\inv{2} M_{ib} y_b
+
\inv{2} y_a M_{ai}
– b_i
=
\lr{ M \By – \Bb }_i.
\end{equation}

The last operation above was possible because \( M = M^\T \). Setting all of these equal to zero, and rewriting this as a matrix relation we have

\begin{equation}\label{eqn:multiphysicsL7:520}
M \By = \Bb,
\end{equation}

as asserted.

This is called the gradient method because the gradient moves us along the path of steepest descent towards the minimum if it exists.

The method is

\begin{equation}\label{eqn:multiphysicsL7:100}
\Bx^{(k+1)} = \Bx^{(k)} +
\underbrace{ \alpha_k }_{step size}
\underbrace{ \Bd^{(k)} }_{direction},
\end{equation}

where the direction is

\begin{equation}\label{eqn:multiphysicsL7:120}
\Bd^{(k)} = – \spacegrad \Phi = \Bb – M \Bx^k = r^{(k)}.
\end{equation}

Optimal step size

Note that for the minimization of \( \Phi \lr{ \Bx^{(k+1)} } \), we note

\begin{equation}\label{eqn:multiphysicsL7:140}
\Phi \lr{ \Bx^{(k+1)} }
= \Phi\lr{ \Bx^{(k)} + \alpha_k \Bd^{(k)} }
=
\inv{2}
\lr{ \Bx^{(k)} + \alpha_k \Bd^{(k)} }^\T
M
\lr{ \Bx^{(k)} + \alpha_k \Bd^{(k)} }
–
\lr{ \Bx^{(k)} + \alpha_k \Bd^{(k)} }^\T \Bb
\end{equation}

If we take the derivative of both sides with respect to \( \alpha_k \) to find the minimum, we have

\begin{equation}\label{eqn:multiphysicsL7:540}
0 =
\inv{2}
\lr{ \Bd^{(k)} }^\T
M
\Bx^{(k)}
+
\inv{2}
\lr{ \Bx^{(k)} }^\T
M
\Bd^{(k)}
+
\alpha_k \lr{ \Bd^{(k)} }^\T
M
\Bd^{(k)}
–
\lr{ \Bd^{(k)} }^\T \Bb.
\end{equation}

Because \( M \) is symmetric, this is

\begin{equation}\label{eqn:multiphysicsL7:560}
\alpha_k \lr{ \Bd^{(k)} }^\T
M
\Bd^{(k)}
=
\lr{ \Bd^{(k)} }^\T \lr{ \Bb – M \Bx^{(k)}}
=
\lr{ \Bd^{(k)} }^\T r^{(k)},
\end{equation}

or

\begin{equation}\label{eqn:multiphysicsL7:160}
\alpha_k
= \frac{
\lr{\Br^{(k)}}^\T
\Br^{(k)}
}{
\lr{\Br^{(k)}}^\T
M
\Br^{(k)}
}
\end{equation}

We will see that this method is not optimal when we pick one direction and keep going down that path.

Definitions and theorems

Definition: Positive (negative) definite

A matrix \( M \) is positive (negative) definite, denoted \( M > 0 (<0) \) if \( \By^\T M \By > 0 (<0), \quad \forall \By \).

If a matrix is neither positive, nor negative definite, it is called indefinite.

Theorem: Positive (negative) definite

A symmetric matrix \( M > 0 (<0)\) iff \( \lambda_i > 0 (<0)\) for all eigenvalues \( \lambda_i \), or is indefinite iff its eigenvalues \( \lambda_i \) are of mixed sign.

References

[1] Harry M Markowitz. The elimination form of the inverse and its application to linear programming. Management Science, 3\penalty0 (3):\penalty0 255–269, 1957.

[2] Timothy Vismor. Pivoting To Preserve Sparsity, 2012. URL https://vismor.com/documents/network_analysis/matrix_algorithms/S8.SS3.php. [Online; accessed 15-Oct-2014].

Differences between Locks, Mutexes, and Semaphores

October 21, 2014 C/C++ development and debugging. , , , , , , , ,

 

James writes to me:

I’m having trouble finding concrete definitions for Locks, Mutexes, and Semaphores

What I do know is:

  • Semaphores keep track of how many processes have gained access (“P”) to a resource and block (suspend and send to priority queue) processes once it’s maxed out. They have no concept of ownership and anyone can call unlock (“V”)
  • Binary semaphores are the same as above except their max is 1
  • Mutexes are the same as a binary semaphore except they have a concept of ownership
  • Spinlocks are the same as mutexes except they do not perform blocking and instead are polled until unlocked

What I don’t know:

Where does the term “lock” fit in here?

  • …Is it a broad category including all of these?
  • …Or is it the equivalent of a mutex but to refer to threads within the same process, as opposed to processes within the same system?
  • …Or is it something else?

What the hell is a lock? I’ve seen the above things referred to as one on some websites but then I’ve seen it listed as a separate thing.

These are all very good definitions.  Before getting to the nebulous term lock, I’d refine the definitions of mutex and spinlocks slightly.  I view these both as constructs that allow exclusive concurrent access by multiple threads or processes to shared memory.

A mutex has a mechanism to ensure that only one “holder” of the mutex resource exists at any point of time, but to be useful, must also include a mechanism to order access of memory protected by that mutex with the memory of the mutex resource itself.  An implementation of a mutex (or spinlock) will have an acquire operation that does

  • an exclusive atomic operation
  • “acquire” (or stronger) memory barrier
  • if the atomic operation fails, there may be code to queue up on an operating system resource (such as a semaphore, or futex)

with the release operation doing:

  • if there are waiters queued up, there may be code to post one or more of these waiters before continuing
  • a “release” memory barrier instruction
  • a store (or atomic) instruction to allow subsequent acquisition.

The memory barriers here are key.   In some cases, appropriate memory barriers may be built into the atomic operations.  For example the intel “LOCK XCHG” on a memory address is atomic and has barrier semantics suitable for an acquire operation.  However, on powerpc, in addition to an atomic operation used to acquire, an instruction like isync will be required to ensure that subsequent memory operations aren’t initiated before the acquire atomic operation has completed.  Similarly, on powerpc, you will need an instruction like “lwsync” on mutex release to ensure that memory operations initiated while the mutex was “held” complete before the store instruction that releases the mutex.

If you did just the following thinking that you have implemented your own mutex:

if ( pSharedMem->mutex.atomicword->atomic_bit_or(1) == successful )
{
   int x = pSharedMem->someInteger ;

   pSharedMem->someValue = v ;

   pSharedMem->mutex.atomicword = 0 ;
}

you would be very disappointed should the underlying hardware execute this as one of

pSharedMem->someValue = v ;

if ( pSharedMem->mutex.atomicword->atomic_bit_or(1) == successful )
{
   int x = pSharedMem->someInteger ;

   pSharedMem->mutex.atomicword = 0 ;
}

or

int x = pSharedMem->someInteger ;

if ( pSharedMem->mutex.atomicword->atomic_bit_or(1) == successful )
{

   pSharedMem->someValue = v ;

   pSharedMem->mutex.atomicword = 0 ;
}

Both of these can occur on platforms that allow out of order execution of memory operations (powerpc, spark, ia64, …) if appropriate memory barrier instructions are not used as part of the mutex implementation.

You would be similarly disappointed with a mutex release operation if it allowed one of the following permutations:

if ( pSharedMem->mutex.atomicword->atomic_bit_or(1) == successful )
{
   int x ;

   pSharedMem->someValue = v ;

   pSharedMem->mutex.atomicword = 0 ;

   x = pSharedMem->someInteger ;
}

or

if ( pSharedMem->mutex.atomicword->atomic_bit_or(1) == successful )
{
   int x = pSharedMem->someInteger ;

   pSharedMem->mutex.atomicword = 0 ;

   pSharedMem->someValue = v ;

}

Both of these permutations can occur on out of order platforms if no appropriate memory barrier instructions are used. This surprises many people that attempt to use atomic operations to avoid contention bottlenecks imposed by a mutex that has significant traffic. One also has to be careful to make sure that the compiler does not move the instructions out of the “mutual exclusion region”. Generally atomic operations (or the plain store above, which could also be implemented with an atomic bitand if required) can be implemented in a way that signals to the compiler that it should not move loads and stores around the atomic.

Now, how about this term “lock”.  The wikipedia definition of lock is fairly consistent with most uses of mutex.  However, it has been my experience that this is defined in whatever way suits the writer.  I have not done an extensive survey, but may also be biased since db2 internals uses “lock” to refer to a serialization mechanism that has a rich set of acquisition modes, as well as concepts of fairness that we don’t have in any of our mutex implementations.

It is common to see lock used in combination.  Examples are spin-locks and reader-writer locks.  I prefer reader writer mutex.  Adding to the confusion, the internal db2 implementation of a reader-writer mutex is referred to as a shared-latch (and we call an exclusive mutex a plain “latch”).  Perhaps this was to distinguish our latch from the already used “lock” term, but before mutex became popular for the same.

My nomenclature preferences are:

  • use mutex for the common sorts of serialization that are required in shared memory multi-thread or multi-procees systems (when talking to db2 developers about generic serialization mechanisms)
  • use spinlock when referring to a mutex that does not use any sort of queuing mechanism for resolving conflict.
  • use semaphore for operating system counting mechanisms (like the unix semop).
  • use lock or latch when talking to db2 developers where these have well defined meaning.
  • use shared latch when talking to db2 developers when I mean reader-writer mutex.

I’d be curious what names other products internal mutex implementations use.

Illustrating the LU algorithm with pivots by example

October 15, 2014 ece1254 , , , ,

[Click here for a PDF of this post with nicer formatting]

Two previous examples of LU factorizations were given. I found one more to be the key to understanding how to implement this as a matlab algorithm, required for our problem set.

A matrix that contains both pivots and elementary matrix operations is

\begin{equation}\label{eqn:luAlgorithm:20}
M=
\begin{bmatrix}
0 & 0 & 2 & 1 \\
0 & 0 & 1 & 1 \\
2 & 0 & 2 & 0 \\
1 & 1 & 1 & 1
\end{bmatrix}
\end{equation}

Our objective is to apply a sequence of row permutations or elementary row operations to \( M \) that put \( M \) into upper triangular form. At the same time we wish to track the all the inverse operations. When no permutations were required to produce \( U \), then we end up with a factorization \( M = L’ U \) where \( L’ \) is lower triangular.

Let’s express the row operations that we apply to \( M \) as

\begin{equation}\label{eqn:luAlgorithm:40}
U =
L_k^{-1}
L_{k-1}^{-1} \cdots
L_2^{-1}
L_1^{-1}
M,
\end{equation}

with

\begin{equation}\label{eqn:luAlgorithm:60}
L’ = L_0 L_1 L_2 \cdots L_{k-1} L_k
\end{equation}

Here \( L_0 = I \), the identity matrix, and \( L_i^{-1} \) is either a permutation matrix interchanging two rows of the identity matrix, or it is an elementary row operation encoding the operation \( r_j \rightarrow r_j – M r_i \), where \( r_i \) is the pivot row, and \( r_j, j > i \) are the rows that we are applying the Gaussian elimination operations to.

For our example matrix, we see that we cannot use the \( M_{1 1} \) as the pivot element since it is zero. In general, for numeric stability, we wish to use the row with the biggest absolute value in the column that we are operating on. In this case that is row 3. Our first row operation is therefore a \( 1,3 \) permutation

\begin{equation}\label{eqn:luAlgorithm:80}
L_1^{-1} =
\begin{bmatrix}
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix},
\end{equation}

which gives us

\begin{equation}\label{eqn:luAlgorithm:100}
M \rightarrow
L_1^{-1}
M
=
\begin{bmatrix}
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
0 & 0 & 2 & 1 \\
0 & 0 & 1 & 1 \\
2 & 0 & 2 & 0 \\
1 & 1 & 1 & 1 \\
\end{bmatrix}
=
\begin{bmatrix}
2 & 0 & 2 & 0 \\
0 & 0 & 1 & 1 \\
0 & 0 & 2 & 1 \\
1 & 1 & 1 & 1 \\
\end{bmatrix}.
\end{equation}

Computationally, we do not wish to actually do a matrix multiplication to achieve this permutation. Instead we want to just swap the two rows in question.

The inverse of this operation is the same permutation, so for \( L’ \) we compute

\begin{equation}\label{eqn:luAlgorithm:120}
L’ \rightarrow L_0 L_1 = L_1.
\end{equation}

As before, we don’t wish to do a matrix operation. Since we have applied the permutation matrix from the right, it results in an exchange of columns \(1,3\) of our \( L_0 \) matrix (which happens to be identity at this point). We can implement that matrix operation as a column exchange directly using submatrix notation.

We now proceed down the column, doing all the non-zero row elimination operations required. In this case, we have only one

\begin{equation}\label{eqn:luAlgorithm:140}
r_4 \rightarrow r_4 – \frac{1}{2} r_1.
\end{equation}

This has the matrix form

\begin{equation}\label{eqn:luAlgorithm:160}
L_2^{-1} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
-1/2 & 0 & 0 & 1 \\
\end{bmatrix}.
\end{equation}

The next stage of the \( U \) computation is

\begin{equation}\label{eqn:luAlgorithm:180}
M
\rightarrow L_2^{-1} L_1^{-1} M
=
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
-1/2 & 0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
2 & 0 & 2 & 0 \\
0 & 0 & 1 & 1 \\
0 & 0 & 2 & 1 \\
1 & 1 & 1 & 1 \\
\end{bmatrix}
=
\begin{bmatrix}
2 & 0 & 2 & 0 \\
0 & 0 & 1 & 1 \\
0 & 0 & 2 & 1 \\
0 & 1 & 0 & 1 \\
\end{bmatrix}.
\end{equation}

Again, we do not wish to do this operation as a matrix operation. Instead we act directly on the rows in question with \ref{eqn:luAlgorithm:140}.

Note that the inverse of this matrix operation is very simple. We’ve subtracted \( r_1/2 \) from \( r_4 \), so to invert this we have only to add back \( r_1/2 \). That is

\begin{equation}\label{eqn:luAlgorithm:200}
L_2
=
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
1/2 & 0 & 0 & 1 \\
\end{bmatrix}.
\end{equation}

Observe that when we apply this from the right to \( L_0 L_1 \rightarrow L_0 L_1 L_2\), the interpretation is a column operation

\begin{equation}\label{eqn:luAlgorithm:220}
c_1 \rightarrow c_1 + m c_4,
\end{equation}

In general, if we apply the row operation

\begin{equation}\label{eqn:luAlgorithm:240}
r_j \rightarrow r_j – m r_i,
\end{equation}

to the current state of our matrix \( U \), then we must apply the operation

\begin{equation}\label{eqn:luAlgorithm:260}
r_i \rightarrow r_i + m r_j,
\end{equation}

to the current state of our matrix \( L’ \).

We are now ready to move on to reduction of column 2. We will have only a permutation operation

\begin{equation}\label{eqn:luAlgorithm:280}
L_3 =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
\end{bmatrix},
\end{equation}

so we apply a \( 2,4 \) row interchange to U, and a \( 2,4 \) column interchange to \( L’ \). This gives us

\begin{equation}\label{eqn:luAlgorithm:300}
M \rightarrow
\begin{bmatrix}
2 & 0 & 2 & 0 \\
0 & 1 & 0 & 1 \\
0 & 0 & 2 & 1 \\
0 & 0 & 1 & 1 \\
\end{bmatrix}.
\end{equation}

Our final operation is a regular row operation

\begin{equation}\label{eqn:luAlgorithm:320}
r_4 \rightarrow r_4 – \inv{2} r_3,
\end{equation}

with matrix
\begin{equation}\label{eqn:luAlgorithm:340}
L_4^{-1} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & -1/2 & 1 \\
\end{bmatrix}
\end{equation}

We can also track all the permutations we have performed, which in this case was

\begin{equation}\label{eqn:luAlgorithm:360}
P = L_3 L_1 I.
\end{equation}

This should also be computed by performing row interchanges, not matrix multiplication.

Now should we wish to solve the system

\begin{equation}\label{eqn:luAlgorithm:380}
M \Bx = L’ U \Bx = \Bb,
\end{equation}

we can equivalently solve

\begin{equation}\label{eqn:luAlgorithm:400}
P L’ U \Bx = P \Bb,
\end{equation}

To do this let \( \By = U \Bx \), so that we wish to solve

\begin{equation}\label{eqn:luAlgorithm:420}
P L’ \By = P \Bb.
\end{equation}

The matrix \( L = P L’ \) is lower triangular, as \( P \) contained all the permutations that we applied along the way (FIXME: this is a statement, not a proof, and not obvious).

We can solve the system

\begin{equation}\label{eqn:luAlgorithm:440}
L \By = P \Bb,
\end{equation}

using forward substitution. That leaves us to solve the upper triangular system

\begin{equation}\label{eqn:luAlgorithm:460}
\By = U \Bx,
\end{equation}

which now requires only back substitution.

Numerical LU example where pivoting is required

October 9, 2014 ece1254 , , ,

[Click here for a PDF of this post with nicer formatting]

I’m having trouble understanding how to apply the LU procedure where pivoting is required. Proceeding with such a factorization, doesn’t produce an LU factorization that is the product of a lower triangular matrix and an upper triangular matrix. What we get instead is what looks like a permutation of a lower triangular matrix with an upper triangular matrix. As an example, consider the LU reduction of

\begin{equation}\label{eqn:luExample2:20}
M \Bx =
\begin{bmatrix}
0 & 0 & 1 \\
2 & 0 & 4 \\
1 & 1 & 1
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
x_3 \\
\end{bmatrix}.
\end{equation}

We want \( r_2 \) as the pivot row, since it has the biggest first column value, so we can write

\begin{equation}\label{eqn:luExample2:40}
M \Bx \rightarrow M’ \Bx’
=
\begin{bmatrix}
2 & 0 & 4 \\
0 & 0 & 1 \\
1 & 1 & 1
\end{bmatrix}
\begin{bmatrix}
x_2 \\
x_1 \\
x_3 \\
\end{bmatrix}.
\end{equation}

We can express this permutation algebraically as a row permutation matrix operation

\begin{equation}\label{eqn:luExample2:60}
M’ =
\begin{bmatrix}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{bmatrix}
M.
\end{equation}

We can now proceed with the Gaussian reduction operations
\begin{equation}\label{eqn:luExample2:80}
\begin{aligned}
r_2 & \rightarrow r_2 – \frac{0}{2} r_1 \\
r_3 & \rightarrow r_3 – \frac{1}{2} r_1 \\
\end{aligned},
\end{equation}

which gives

\begin{equation}\label{eqn:luExample2:100}
M_1 =
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
-1/2 & 0 & 1
\end{bmatrix}
M’
=
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
-1/2 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
2 & 0 & 4 \\
0 & 0 & 1 \\
1 & 1 & 1
\end{bmatrix}
=
\begin{bmatrix}
2 & 0 & 4 \\
0 & 0 & 1 \\
0 & 1 & -1
\end{bmatrix}.
\end{equation}

Application of one more permutation operation gives us the desired upper triangular matrix

\begin{equation}\label{eqn:luExample2:120}
U = M_1′ =
\begin{bmatrix}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0 \\
\end{bmatrix}
\begin{bmatrix}
2 & 0 & 4 \\
0 & 0 & 1 \\
0 & 1 & -1
\end{bmatrix}
=
\begin{bmatrix}
2 & 0 & 4 \\
0 & 1 & -1 \\
0 & 0 & 1
\end{bmatrix}.
\end{equation}

This new matrix operator applies to the permuted vector

\begin{equation}\label{eqn:luExample2:140}
\Bx” =
\begin{bmatrix}
x_2 \\
x_3 \\
x_1 \\
\end{bmatrix}.
\end{equation}

We’ve constructed \( U \) by the following row operations

\begin{equation}\label{eqn:luExample2:160}
U =
\begin{bmatrix}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0 \\
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
-1/2 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
M.
\end{equation}

Seeking \( L U = M \), we want

\begin{equation}\label{eqn:luExample2:180}
L
\begin{bmatrix}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0 \\
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
-1/2 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
M
= M,
\end{equation}

or

\begin{equation}\label{eqn:luExample2:200}
L
=
\begin{bmatrix}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
1/2 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0 \\
\end{bmatrix}
=
\begin{bmatrix}
0 & 1 & 0 \\
1 & 0 & 0 \\
1/2 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0 \\
\end{bmatrix}
=
\begin{bmatrix}
0 & 0 & 1 \\
1 & 0 & 0 \\
1/2 & 1 & 0
\end{bmatrix}.
\end{equation}

The \( L U \) factorization that we’ve attempted does not appear to produce a lower triangular factor, but a permutation of a lower triangular factor?

When such pivoting is required it isn’t obvious, at least to me, how to do the clever \( L U \) algorithm that we outlined in class. How can we pack the operations into the lower triangle when we actually have to apply permutation matrices to the results of the last iteration.

It seems that while we cannot perform a \( LU \) decomposition of \( M \) we can perform an \( L U \) factorization of \( P M \), where \( P \) is the permutation matrix for the permutation \( 2,3,1 \) that we applied to the rows during the Gaussian operations.

Let’s do that \( L U \) factorization to check

\begin{equation}\label{eqn:luExample2:220}
P M =
\begin{bmatrix}
0 & 1 & 0 \\
0 & 0 & 1 \\
1 & 0 & 0 \\
\end{bmatrix}
\begin{bmatrix}
0 & 0 & 1 \\
2 & 0 & 4 \\
1 & 1 & 1
\end{bmatrix}
=
\begin{bmatrix}
2 & 0 & 4 \\
1 & 1 & 1 \\
0 & 0 & 1 \\
\end{bmatrix}.
\end{equation}

We want to apply the elementary row operation

\begin{equation}\label{eqn:luExample2:240}
r_2 \rightarrow r_2 – \frac{1}{2} r_1,
\end{equation}

for

\begin{equation}\label{eqn:luExample2:260}
\lr{P M}_1 =
\begin{bmatrix}
2 & 0 & 4 \\
0 & 1 & -1 \\
0 & 0 & 1 \\
\end{bmatrix},
\end{equation}

The \( L U \) factorization is therefore

\begin{equation}\label{eqn:luExample2:280}
P M =
L U =
\begin{bmatrix}
1 & 0 & 0 \\
1/2 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
2 & 0 & 4 \\
0 & 1 & -1 \\
0 & 0 & 1 \\
\end{bmatrix}.
\end{equation}

Observe that we can also write this as

\begin{equation}\label{eqn:luExample2:300}
M = \lr{ P^{-1} L } U.
\end{equation}

In our case the inverse permutation is a \( 3,1,2 \) permutation matrix

\begin{equation}\label{eqn:luExample2:320}
P^{-1} =
\begin{bmatrix}
0 & 0 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0 \\
\end{bmatrix}.
\end{equation}

We see that \( P^{-1} L \) produces the not-lower-triangular matrix factor found earlier in \ref{eqn:luExample2:200}.

Numeric LU factorization example

October 9, 2014 ece1254 , , ,

[Click here for a PDF of this post with nicer formatting]

To get a better feel for LU factorization before attempting a numeric implementation, let’s look at a numeric example in detail. This will strip some of the abstraction away.

Let’s compute the LU factorization for

\begin{equation}\label{eqn:luExample:20}
M =
\begin{bmatrix}
5 & 1 & 1 \\
2 & 3 & 4 \\
3 & 1 & 2 \\
\end{bmatrix}.
\end{equation}

This matrix was picked to avoid having to think of selecting the right pivot
row. The first two operations are

\begin{equation}\label{eqn:luExample:41}
\begin{aligned}
r_2 &\rightarrow r_2 – \frac{2}{5} r_1 \\
r_3 &\rightarrow r_3 – \frac{3}{5} r_1
\end{aligned},
\end{equation}

and produce
\begin{equation}\label{eqn:luExample:40}
\begin{bmatrix}
5 & 1 & 1 \\
0 &13/5 & 18/5 \\
0 &2/5 & 7/5 \\
\end{bmatrix}
\end{equation}

The row operations (left multiplication) that produce this matrix are

\begin{equation}\label{eqn:luExample:60}
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
-3/5 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
-2/5 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & 0 \\
-2/5 & 1 & 0 \\
-3/5 & 0 & 1 \\
\end{bmatrix}.
\end{equation}

These operations happen to be commutative and also both invert simply. The inverse operations are
\begin{equation}\label{eqn:luExample:80}
\begin{bmatrix}
1 & 0 & 0 \\
2/5 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
3/5 & 0 & 1 \\
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & 0 \\
2/5 & 1 & 0 \\
3/5 & 0 & 1 \\
\end{bmatrix}.
\end{equation}

In matrix form the elementary matrix operations that take us to the first stage of the Gaussian reduction are

\begin{equation}\label{eqn:luExample:100}
\begin{bmatrix}
1 & 0 & 0 \\
-2/5 & 1 & 0 \\
-3/5 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
5 & 1 & 1 \\
2 & 3 & 4 \\
3 & 1 & 2 \\
\end{bmatrix}
=
\begin{bmatrix}
5 & 1 & 1 \\
0 &13/5 & 18/5 \\
0 &2/5 & 7/5 \\
\end{bmatrix}.
\end{equation}

Inverted that is

\begin{equation}\label{eqn:luExample:120}
\begin{bmatrix}
5 & 1 & 1 \\
2 & 3 & 4 \\
3 & 1 & 2 \\
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & 0 \\
2/5 & 1 & 0 \\
3/5 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
5 & 1 & 1 \\
0 &13/5 & 18/5 \\
0 &2/5 & 7/5 \\
\end{bmatrix}.
\end{equation}

This is the first stage of the LU decomposition, although the U matrix is not yet in upper triangular form. Again, with our pivot row in the desired position already, the last row operation to perform is

\begin{equation}\label{eqn:luExample:140}
r_3 \rightarrow r_3 – \frac{2/5}{5/13} r_2 = r_3 – \frac{2}{13} r_2.
\end{equation}

The final stage of this Gaussian reduction is

\begin{equation}\label{eqn:luExample:160}
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & -2/13 & 1 \\
\end{bmatrix}
\begin{bmatrix}
5 & 1 & 1 \\
0 &13/5 & 18/5 \\
0 &2/5 & 7/5 \\
\end{bmatrix}
=
\begin{bmatrix}
5 & 1 & 1 \\
0 &13/5 & 18/5 \\
0 & 0 & 11/13 \\
\end{bmatrix}
= U,
\end{equation}

and our desired lower triangular matrix factor is
\begin{equation}\label{eqn:luExample:180}
\begin{bmatrix}
1 & 0 & 0 \\
2/5 & 1 & 0 \\
3/5 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 2/13 & 1 \\
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & 0 \\
2/5 & 1 & 0 \\
3/5 & 2/13 & 1 \\
\end{bmatrix}
= L.
\end{equation}

A bit of matlab code easily verifies that the above manual computation recovers \( M = L U \) 

l = [ 1 0 0 ; 2/5 1 0 ; 3/5 2/13 1 ] ;
u = [ 5 1 1 ; 0 13/5 18/5 ; 0 0 11/13 ] ;
m = l * u