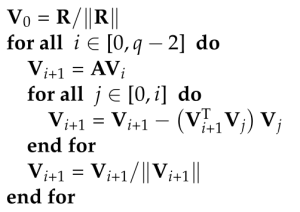Month: November 2014

Laplace transform refresher

November 27, 2014 ece1254 , , , ,

[Click here for a PDF of this post with nicer formatting]

Laplace transforms were used to solve the MNA equations for time dependent systems, and to find the moments used to in MOR.

For the record, the Laplace transform is defined as:

\begin{equation}\label{eqn:laplaceTransformVec:20}
\boxed{
\LL( f(t) ) =
\int_0^\infty e^{-s t} f(t) dt.
}
\end{equation}

The only Laplace transform pair used in the lectures is that of the first derivative

\begin{equation}\label{eqn:laplaceTransformVec:40}
\begin{aligned}
\LL(f'(t)) &=
\int_0^\infty e^{-s t} \ddt{f(t)} dt \\
&=
\evalrange{e^{-s t} f(t)}{0}{\infty} – (-s) \int_0^\infty e^{-s t} f(t) dt \\
&=
-f(0) + s \LL(f(t)).
\end{aligned}
\end{equation}

Here it is loosely assumed that the real part of \( s \) is positive, and that \( f(t) \) is “well defined” enough that \( e^{-s \infty } f(\infty) \rightarrow 0 \).

Where used in the lectures, the laplace transforms were of vectors such as the matrix vector product \( \LL(\BG \Bx(t)) \). Because such a product is linear, observe that it can be expressed as the original matrix times a vector of Laplace transforms

\begin{equation}\label{eqn:laplaceTransformVec:60}
\begin{aligned}
\LL( \BG \Bx(t) )
&=
\LL {\begin{bmatrix}
G_{i k} x_k(t)
\end{bmatrix}}_i \\
&=
{\begin{bmatrix}
G_{i k} \LL x_k(t)
\end{bmatrix}}_i \\
&=
\BG
{\begin{bmatrix}
\LL x_i(t)
\end{bmatrix}}_i.
\end{aligned}
\end{equation}

The following notation was used in the lectures for such a vector of Laplace transforms

\begin{equation}\label{eqn:laplaceTransformVec:80}
\BX(s) = \LL \Bx(t) =
{\begin{bmatrix}
\LL x_i(t)
\end{bmatrix}}_i.
\end{equation}

ECE1254H Modeling of Multiphysics Systems. Lecture 19: Model order reduction (cont).. Taught by Prof. Piero Triverio

November 26, 2014 ece1254 , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

Model order reduction (cont).

An approximation of the following system is sought

\begin{equation}\label{eqn:multiphysicsL19:20}
\BG \Bx(t) + C \dot{\Bx}(t) = B \Bu(t)
\end{equation}
\begin{equation}\label{eqn:multiphysicsL19:40}
\By(t) = \BL^\T \Bx(t).
\end{equation}

The strategy is to attempt to find a \( N \times q \) projector \( \BV \) of the form

\begin{equation}\label{eqn:multiphysicsL19:60}
\BV =
\begin{bmatrix}
\Bv_1 & \Bv_2 & \cdots & \Bv_q
\end{bmatrix}
\end{equation}

so that the solution of the constrained q-variable state vector \( \Bx_q \) is sought after letting

\begin{equation}\label{eqn:multiphysicsL19:80}
\Bx(t) = \BV \Bx_q(t).
\end{equation}

Moment matching

\begin{equation}\label{eqn:multiphysicsL19:100}
\begin{aligned}
\BF(s)
&= \lr{ \BG + s \BC }^{-1} \BB \\
&= \BM_0 + \BM_1 s + \BM_2 s^2 + \cdots + \BM_{q-1} s^{q-1} + M_q s^q + \cdots
\end{aligned}
\end{equation}

The reduced model is created such that

\begin{equation}\label{eqn:multiphysicsProblemSet3b:120}
\BF_q(s)
=
\BM_0 + \BM_1 s + \BM_2 s^2 + \cdots + \BM_{q-1} s^{q-1} + \tilde{\BM}_q s^q.
\end{equation}

Form an \( N \times q \) projection matrix

\begin{equation}\label{eqn:multiphysicsL19:140}
\BV_q \equiv
\begin{bmatrix}
\BM_0 & \BM_1 & \cdots & \BM_{q-1}
\end{bmatrix}
\end{equation}

With the substitution of fig. 1, becomes

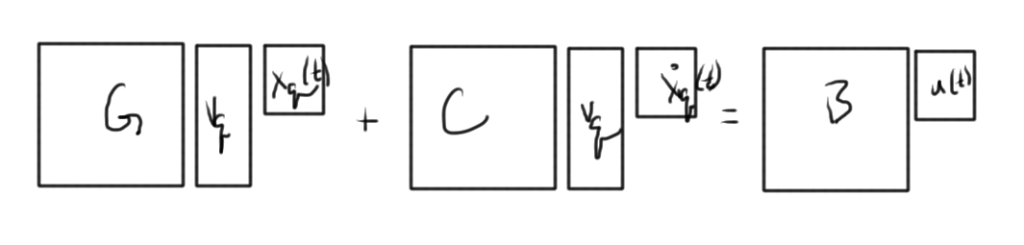
lecture19Fig1

This is a system of \( N \) equations, in \( q \) unknowns. A set of moments from the frequency domain have been used to project the time domain system. This relies on the following unproved theorem (references to come)

Theorem

If \( \text{span}\{ \Bv_q \} = \text{span} \{ \BM_0, \BM_1, \cdots, \BM_{q-1} \} \), then the reduced model will match the first \( q \) moments.

Left multiplication by \( \BV_q^\T \) yields fig. 2.

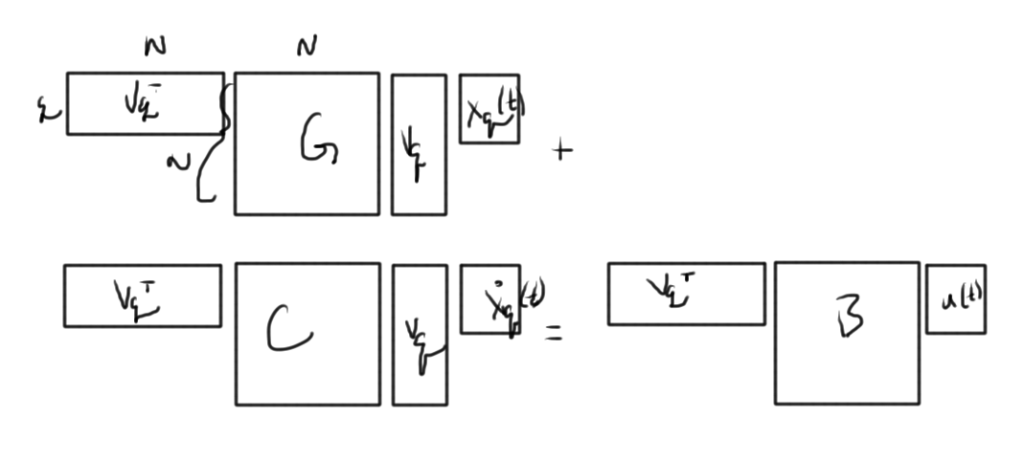
lecture19Fig2

This is now a system of \( q \) equations in \( q \) unknowns.

With

\begin{equation}\label{eqn:multiphysicsL19:160}
\BG_q = \BV_q^\T \BG \BV_q
\end{equation}
\begin{equation}\label{eqn:multiphysicsL19:180}
\BC_q = \BV_q^\T \BC \BV_q
\end{equation}
\begin{equation}\label{eqn:multiphysicsL19:200}
\BB_q = \BV_q^\T \BB
\end{equation}
\begin{equation}\label{eqn:multiphysicsL19:220}
\BL_q^\T = \BL^\T \BV_q
\end{equation}

the system is reduced to

\begin{equation}\label{eqn:multiphysicsL19:240}
\BG_q \Bx_q(t) + \BC_q \dot{\Bx}_q(t) = \BB_q \Bu(t).
\end{equation}
\begin{equation}\label{eqn:multiphysicsL19:260}
\By(t) \approx \BL_q^\T \Bx_q(t)
\end{equation}

Moments calculation

Using
\begin{equation}\label{eqn:multiphysicsL19:300}
\lr{ \BG + s \BC }^{-1} \BB = \BM_0 + \BM_1 s + \BM_2 s^2 + \cdots
\end{equation}

thus
\begin{equation}\label{eqn:multiphysicsL19:320}
\begin{aligned}
\BB &=
\lr{ \BG + s \BC }
\BM_0 +
\lr{ \BG + s \BC }
\BM_1 s +
\lr{ \BG + s \BC }
\BM_2 s^2 + \cdots \\
&=
\BG \BM_0
+ s \lr{ C \BM_0 + \BG \BM_1 }
+ s^2 \lr{ C \BM_1 + \BG \BM_2 }
+ \cdots
\end{aligned}
\end{equation}

Since \( \BB \) is a zeroth order matrix, setting all the coefficients of \( s \) equal to zero provides a method to solve for the moments

\begin{equation}\label{eqn:multiphysicsL19:340}
\begin{aligned}
\BB &= \BG \BM_0 \\
-\BC \BM_0 &= \BG \BM_1 \\
-\BC \BM_1 &= \BG \BM_2 \\
\end{aligned}
\end{equation}

The moment \( \BM_0 \) can be found with LU of \( \BG \), plus the forward and backward substitutions. Proceeding recursively, using the already computed LU factorization, each subsequent moment calculation requires only one pair of forward and backward substitutions.

Numerically, each moment has the exact value

\begin{equation}\label{eqn:multiphysicsL19:360}
\BM_q = \lr{- \BG^{-1} \BC }^q \BM_0.
\end{equation}

As \( q \rightarrow \infty \), this goes to some limit, say \( \Bw \). The value \( \Bw \) is related to the largest eigenvalue of \( -\BG^{-1} \BC \). Incidentally, this can be used to find the largest eigenvalue of \( -\BG^{-1} \BC \).

The largest eigenvalue of this matrix will dominate these factors, and can cause some numerical trouble. For this reason it is desirable to avoid such explicit moment determination, instead using implicit methods.

The key is to utilize the theorem above, and look instead for an alternate basis \( \{ \Bv_q \} \) that also spans \( \{ \BM_0, \BM_1, \cdots, \BM_q \} \).

Space generate by the moments

Write

\begin{equation}\label{eqn:multiphysicsL19:380}
\BM_q = \BA^q \BR,
\end{equation}

where in this case

\begin{equation}\label{eqn:multiphysicsL19:400}
\begin{aligned}
\BA &= – \BG^{-1} \BC \\
\BR &= \BM_0 = -\BG \BB
\end{aligned}
\end{equation}

The span of interest is

\begin{equation}\label{eqn:multiphysicsL19:420}
\text{span} \{ \BR, \BA \BR, \BA^2 \BR, \cdots, \BA^{q-1} \BR \}.
\end{equation}

Such a sequence is called a Krylov subspace. One method to compute such a basis, the Arnoldi process, relies on Gram-Schmidt orthonormalization methods:

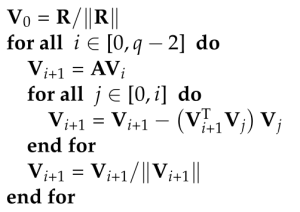
arnoldi

Some numerical examples and plots on the class slides.

Stability of discretized linear differential equations

November 17, 2014 ece1254 , , , ,

[Click here for a PDF of this post with nicer formatting]

In class today was a highlight of stability methods for linear multistep methods. To motivate the methods used, it is helpful to take a step back and review stability concepts for LDE systems.

By way of example, consider a second order LDE homogeneous system defined by

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:20}
\frac{d^2 x}{dt^2} + 3 \frac{dx}{dt} + 2 = 0.
\end{equation}

Such a system can be solved by assuming an exponential solution, say

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:40}
x(t) = e^{s t}.
\end{equation}

Substitution gives

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:60}
e^{st} \lr{ s^2 + 3 s + 2 } = 0,
\end{equation}

The polynomial part of this equation, the characteristic equation has roots \( s = -2, -1 \).

The general solution of \ref{eqn:stabilityLDEandDiscreteTime:20} is formed by a superposition of solutions for each value of \(s\)

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:80}
x(t) = a e^{-2 t} + b e^{-t}.
\end{equation}

Independent of any selection of the superposition constants \( a, b \), this function will not blow up as \( t \rightarrow \infty \).

This “stability” is due to the fact that both of the characteristic equation roots lie in the left hand Argand plane.

Now consider a discretized form of this LDE. This will have the form

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:100}
\begin{aligned}
0 &=
\inv{\lr{\Delta t}^2}
\lr{ x_{n+2} – 2 x_{n-1} + x_n } + \frac{3}{\Delta t} \lr{ x_{n+1} – x_n } + 2
x_n \\
&=
x_{n+2} \lr{
\inv{\lr{\Delta t}^2}
}
+
x_{n+1} \lr{
\frac{3}{\Delta t}
-\frac{2}{\lr{\Delta t}^2}
}
+
x_{n} \lr{
\frac{1}{\lr{\Delta t}^2}
-\frac{3}{\Delta t}
+ 2
},
\end{aligned}
\end{equation}

or

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:220}
0
=
x_{n+2}
+
x_{n+1} \lr{
3 \Delta t – 2
}
+
x_{n} \lr{
1 – 3 \Delta t + 2 \lr{ \Delta t}^2
}.
\end{equation}

Note that after discretization, each subsequent index corresponds to a time shift. Also observe that the coefficients of this discretized equation are dependent on the discretization interval size \( \Delta t \). If the specifics of those coefficients are ignored, a general form with the following structure can be observed

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:120}
0 =
x_{n+2} \gamma_0
+
x_{n+1} \gamma_1
+
x_{n} \gamma_2.
\end{equation}

It turns out that, much like the LDE solution by characteristic polynomial, it is possible to attack this problem by assuming a solution of the form

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:140}
x_n = C z^n.
\end{equation}

A time shift index change \( x_n \rightarrow x_{n+1} \) results in a power adjustment in this assumed solution. This substitution applied to \ref{eqn:stabilityLDEandDiscreteTime:120} yields

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:160}
0 =
C z^n
\lr{
z^{2} \gamma_0
+
z \gamma_1
+
1 \gamma_2
},
\end{equation}

Suppose that this polynomial has roots \( z \in \{z_1, z_2\} \). A superposition, such as

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:180}
x_n = a z_1^n + b z_2^n,
\end{equation}

will also be a solution since insertion of this into the RHS of \ref{eqn:stabilityLDEandDiscreteTime:120} yields

\begin{equation}\label{eqn:stabilityLDEandDiscreteTime:200}
a z_1^n
\lr{
z_1^{2} \gamma_0
+
z_1 \gamma_1
+
\gamma_2
}
+
b
z_2^n
\lr{
z_2^{2} \gamma_0
+
z_2 \gamma_1
+
\gamma_2
}
=
a z_1^n \times 0
+b z_2^n \times 0.
\end{equation}

The zero equality follows since \( z_1, z_2 \) are both roots of the characteristic equation for this discretized LDE.
In the discrete \( z \) domain stability requires that the roots satisfy the bound \( \Abs{z} < 1 \), a different stability criteria than in the continuous domain. In fact, there is no a-priori guarantee that stability in the continuous domain will imply stability in the discretized domain. Let's plot those z-domain roots for this example LDE, using \( \Delta t \in \{ 1/2, 1, 2 \} \). The respective characteristic polynomials are \begin{equation}\label{eqn:stabilityLDEandDiscreteTime:260} 0 = z^2 - \inv{2} z = z \lr{ z - \inv{2} } \end{equation} \begin{equation}\label{eqn:stabilityLDEandDiscreteTime:240} 0 = z^2 + z = z\lr{ z + 1 } \end{equation} \begin{equation}\label{eqn:stabilityLDEandDiscreteTime:280} 0 = z^2 + 4 z + 3 = (z + 3)(z + 1). \end{equation} These have respective roots \begin{equation}\label{eqn:stabilityLDEandDiscreteTime:300} z = 0, \inv{2} \end{equation} \begin{equation}\label{eqn:stabilityLDEandDiscreteTime:320} z = 0, -1 \end{equation} \begin{equation}\label{eqn:stabilityLDEandDiscreteTime:340} z = -1, -3 \end{equation} Only the first discretization of these three yields stable solutions in the z domain, although it appears that \( \Delta t = 1 \) is right on the boundary.

ECE1254H Modeling of Multiphysics Systems. Lecture 16: LMS systems and stability. Taught by Prof. Piero Triverio

November 17, 2014 ece1254 , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

Residual for LMS methods

Mostly on slides:

12_ODS.pdf

Residual is illustrated in fig. 1, assuming that the iterative method was accurate until \( t_{n} \)

lecture16Fig1

fig. 1. Residual illustrated

 

Summary

  • [FE]: \( R_{n+1} \sim \lr{ \Delta t}^2 \). This is of order \( p = 1 \).
  • [BE]: \( R_{n+1} \sim \lr{ \Delta t}^2 \). This is of order \( p = 1 \).
  • [TR]: \( R_{n+1} \sim \lr{ \Delta t}^3 \). This is of order \( p = 2 \).
  • [BESTE]: \( R_{n+1} \sim \lr{ \Delta t}^4 \). This is of order \( p = 3 \).

Global error estimate

Suppose \( t \in [0, 1] s \), with \( N = 1/{\Delta t} \) intervals. For a method with local error of order \( R_{n+1} \sim \lr{ \Delta t}^2 \) the global error is approximately \( N R_{n+1} \sim \Delta t \).

Stability

Recall that a linear multistep method (LMS) was a system of the form

\begin{equation}\label{eqn:multiphysicsL16:20}
\sum_{j=-1}^{k-1} \alpha_j x_{n-j} = \Delta t \sum_{j=-1}^{k-1} \beta_j f( x_{n-j}, t_{n-j} )
\end{equation}

Consider a one dimensional test problem

\begin{equation}\label{eqn:multiphysicsL16:40}
\dot{x}(t) = \lambda x(t)
\end{equation}

where as in fig. 2, \( \Re(\lambda) < 0 \) is assumed to ensure stability.

lecture16Fig2

fig. 2. Stable system

 

Linear stability theory can be thought of as asking the question: “Is the solution of \ref{eqn:multiphysicsL16:40} computed by my LMS method also stable?”

Application of \ref{eqn:multiphysicsL16:20} to \ref{eqn:multiphysicsL16:40} gives

\begin{equation}\label{eqn:multiphysicsL16:60}
\sum_{j=-1}^{k-1} \alpha_j x_{n-j} = \Delta t \sum_{j=-1}^{k-1} \beta_j \lambda x_{n-j},
\end{equation}

or
\begin{equation}\label{eqn:multiphysicsL16:80}
\sum_{j=-1}^{k-1} \lr{ \alpha_j – \Delta \beta_j \lambda }
x_{n-j} = 0.
\end{equation}

With

\begin{equation}\label{eqn:multiphysicsL16:100}
\gamma_j = \alpha_j – \Delta \beta_j \lambda,
\end{equation}

this expands to
\begin{equation}\label{eqn:multiphysicsL16:120}
\gamma_{-1} x_{n+1}
+
\gamma_{0} x_{n}
+
\gamma_{1} x_{n-1}
+
\cdots
+
\gamma_{k-1} x_{n-k} .
\end{equation}

This can be seen as a

  • discrete time system
  • FIR filter

The numerical solution \( x_n \) will be stable if \ref{eqn:multiphysicsL16:120} is stable.

A characteristic equation associated with \ref{eqn:multiphysicsL16:120} can be defined as

\begin{equation}\label{eqn:multiphysicsL16:140}
\gamma_{-1} z^k
+
\gamma_{0} z^{k-1}
+
\gamma_{1} z^{k-2}
+
\cdots
+
\gamma_{k-1} = 0.
\end{equation}

This is a polynomial with roots \( z_n \) (poles). This is stable if the poles satisfy \( \Abs{z_n} < 1 \), as illustrated in fig. 3

lecture16Fig3

Stability

 

Observe that the \( \gamma’s \) are dependent on \( \Delta t \).

FIXME: There’s a lot of handwaving here that could use more strict justification. Check if the text covers this in more detail.

Example: Forward Euler stability

For \( k = 1 \) step.

\begin{equation}\label{eqn:multiphysicsL16:180}
x_{n+1} – x_n = \Delta t f( x_n, t_n ),
\end{equation}

the coefficients are \( \alpha_{-1} = 1, \alpha_0 = -1, \beta_{-1} = 0, \beta_0 =1 \). For the simple function above

\begin{equation}\label{eqn:multiphysicsL16:200}
\gamma_{-1} = \alpha_{-1} – \Delta t \lambda \beta_{-1} = 1
\end{equation}
\begin{equation}\label{eqn:multiphysicsL16:220}
\gamma_{0} = \alpha_{0} – \Delta t \lambda \beta_{0} = -1 – \Delta t \lambda.
\end{equation}

The stability polynomial is

\begin{equation}\label{eqn:multiphysicsL16:240}
1 z + \lr{ -1 – \Delta t \lambda} = 0,
\end{equation}

or

\begin{equation}\label{eqn:multiphysicsL16:260}
\boxed{
z = 1 + \delta t \lambda.
}
\end{equation}

This is the root, or pole.

For stability we must have

\begin{equation}\label{eqn:multiphysicsL16:280}
\Abs{ 1 + \Delta t \lambda } < 1,
\end{equation}

or
\begin{equation}\label{eqn:multiphysicsL16:300}
\Abs{ \lambda – \lr{ -\inv{\Delta t} } } < \inv{\Delta t},
\end{equation}

This inequality is illustrated roughly in fig. 4.

lecture16Fig4

fig. 4. Stability region of FE

 

All poles of my system must be inside the stability region in order to get stable \( \gamma \).

resolving merge conflicts due to automated C to C++ comment changes

November 17, 2014 C/C++ development and debugging. , , , ,

I was faced with hundreds of merge conflicts that had the following diff3 -m conflict structure:


<<<<<<< file.C.mine
   /* Allocate memory for ProcNamePattern and memset to blank */
   /* ProcNamePattern is used as an intermediate upper case string to capture the procedure name*/
   /* Allocate space for 128 byte schema, 128 byte procedure name */
   rc = BAR(0,
            len+SCHEMA_IDENT+1,
            MEM_DEFAULT,
            &ProcNamePattern);
||||||| file.C.orig
   /* Allocate memory for ProcNamePattern and memset to blank */
   /* ProcNamePattern is used as an intermediate upper case string to capture the procedure name*/
   /* Allocate space for 128 byte schema, 128 byte procedure name */
   rc = FOO(0,
            len+SCHEMA_IDENT+1,
            (void **) &ProcNamePattern);
=======
   // Allocate memory for ProcNamePattern and memset to blank
   // ProcNamePattern is used as an intermediate upper case string to capture the procedure name
   // Allocate space for 128 byte schema, 128 byte procedure name
   rc = FOO(0,
            len+SCHEMA_IDENT+1,
            (void **) &ProcNamePattern);
>>>>>>> file.C.new
   if (rc  )
   {

I’d run a clang based source editing tool that changed FOO to BAR, added a parameter, and removed a cast. Other maintainers of the code had run a tool, or perhaps an editor macro that changed most (but not all) of the C style /* … */ comments into C++ single line comments // …

Those pairs of changes were unfortunately close enough to generate a diff3 -m conflict.

I can run my clang editing tool again (and will), but need to get the source compile-able first, so was faced with either tossing and regenerating my changes, or resolving the conflicts. Basically I needed to filter these comments in the same fashion, and then accept all of my changes, provided there were no other changes in the .orig -> .new stream.

Here’s a little perl filter I wrote for this task:

#!/usr/bin/perl -n

# a script to replace single line /* */ comments with C++ // comments in a restricted fashion.
#
# - doesn't touch comments of the form:
#                                         /* ... */ ... /* ...
#                                         ^^            ^^
# - doesn't touch comments with leading non-whitespace or trailing non-whitespace
#
# This is used to filter new/old/mine triplets in merges to deal with automated replacements of this sort.

chomp ;

if ( ! m,/\*.*/\*, )
{
   s,
^(\s*)   # restrict replacement to comments that start only after beginning of line and whitespace
/\*      # start of comment
\s*      # opt spaces
(.*)     # payload
\s*      # opt spaces
\*/      # end of comment
\s*$     # opt spaces and end of line
,$1// $2,x ;
}

#s,/\* *(.*)(?=\*/ *$)\*/ *$,// $1, ;

print "$_\n" ;

This consumes stdin, and spits out stdout, making the automated change that had been applied to the code. I didn’t want it to do anything with comments of any of the forms:

  • [non-whitespace] /* … */
  • /* … */ … non-whitespace
  • /* … */ … /* … */

Since the comment filtering that’s now in the current version of the files didn’t do this, and I didn’t want to introduce more conflicts due to spacing changes.

With this filter run on all the .mine, .orig, .new versions I was able to rerun

diff3 -m file.mine file.orig file.new

and have only a few actual conflicts to deal with. Most of those were also due to space change and in some cases comment removal.

A lot of this trouble stems from the fact that our product has no coding standards for layout (or very little, or ones that are component specific). I maintain our coding standards for correctness, but when I was given these standards as fairly green developer I didn’t have the guts to take on the role of coding standards dictator, and impose style guidelines on developers very much my senior.

Without style guidelines, a lot of these sorts of merge conflicts could be avoided or minimized significantly if we would only make automated changes with tools that everybody could (or must) run. That would allow conflict filtering of those sort to be done automatically, without having to write ad-hoc tools to “re-play” the automated change in a subset of the merge contributors.

My use of a clang rewriter flies in the face of this ideal conflict avoidance strategy since our build environment is not currently tooled up for our development to do so. However, in this case, being able to do robust automated maintenance ill hopefully be worth the conflicts that this itself will inject.