[Click here for a PDF of this post with nicer formatting]
Recall that the relativistic form of Maxwell’s equation in Geometric Algebra is
\begin{equation}\label{eqn:maxwellStokes:20}
\grad F = \inv{c \epsilon_0} J.
\end{equation}
where \( \grad = \gamma^\mu \partial_\mu \) is the spacetime gradient, and \( J = (c\rho, \BJ) = J^\mu \gamma_\mu \) is the four (vector) current density. The pseudoscalar for the space is denoted \( I = \gamma_0 \gamma_1 \gamma_2 \gamma_3 \), where the basis elements satisfy \( \gamma_0^2 = 1 = -\gamma_k^2 \), and a dual basis satisfies \( \gamma_\mu \cdot \gamma^\nu = \delta_\mu^\nu \). The electromagnetic field \( F \) is a composite multivector \( F = \BE + I c \BB \). This is actually a bivector because spatial vectors have a bivector representation in the space time algebra of the form \( \BE = E^k \gamma_k \gamma_0 \).
Previously, I wrote out the Stokes integrals for Maxwell’s equation in GA form using some three parameter spacetime manifold volumes. This time I’m going to use two and three parameter spatial volumes, again with the Geometric Algebra form of Stokes theorem.
Multiplication by a timelike unit vector transforms Maxwell’s equation from their relativistic form. When that vector is the standard basis timelike unit vector \( \gamma_0 \), we obtain Maxwell’s equations from the point of view of a stationary observer
\begin{equation}\label{eqn:stokesMaxwellSpaceTimeSplit:40}
\lr{\partial_0 + \spacegrad} \lr{ \BE + c I \BB } = \inv{\epsilon_0 c} \lr{ c \rho – \BJ },
\end{equation}
Extracting the scalar, vector, bivector, and trivector grades respectively, we have
\begin{equation}\label{eqn:stokesMaxwellSpaceTimeSplit:60}
\begin{aligned}
\spacegrad \cdot \BE &= \frac{\rho}{\epsilon_0} \\
c I \spacegrad \wedge \BB &= -\partial_0 \BE – \inv{\epsilon_0 c} \BJ \\
\spacegrad \wedge \BE &= – I c \partial_0 \BB \\
c I \spacegrad \cdot \BB &= 0.
\end{aligned}
\end{equation}
Each of these can be written as a curl equation
\begin{equation}\label{eqn:stokesMaxwellSpaceTimeSplit:80}
\boxed{
\begin{aligned}
\spacegrad \wedge (I \BE) &= I \frac{\rho}{\epsilon_0} \\
\inv{\mu_0} \spacegrad \wedge \BB &= \epsilon_0 I \partial_t \BE + I \BJ \\
\spacegrad \wedge \BE &= -I \partial_t \BB \\
\spacegrad \wedge (I \BB) &= 0,
\end{aligned}
}
\end{equation}
a form that allows for direct application of Stokes integrals. The first and last of these require a three parameter volume element, whereas the two bivector grade equations can be integrated using either two or three parameter volume elements. Suppose that we have can parameterize the space with parameters \( u, v, w \), for which the gradient has the representation
\begin{equation}\label{eqn:stokesMaxwellSpaceTimeSplit:100}
\spacegrad = \Bx^u \partial_u + \Bx^v \partial_v + \Bx^w \partial_w,
\end{equation}
but we integrate over a two parameter subset of this space spanned by \( \Bx(u,v) \), with area element
\begin{equation}\label{eqn:stokesMaxwellSpaceTimeSplit:120}
\begin{aligned}
d^2 \Bx
&= d\Bx_u \wedge d\Bx_v \\
&=
\PD{u}{\Bx}
\wedge
\PD{v}{\Bx}
\,du dv \\
&=
\Bx_u
\wedge
\Bx_v
\,du dv,
\end{aligned}
\end{equation}
as illustrated in fig. 1.
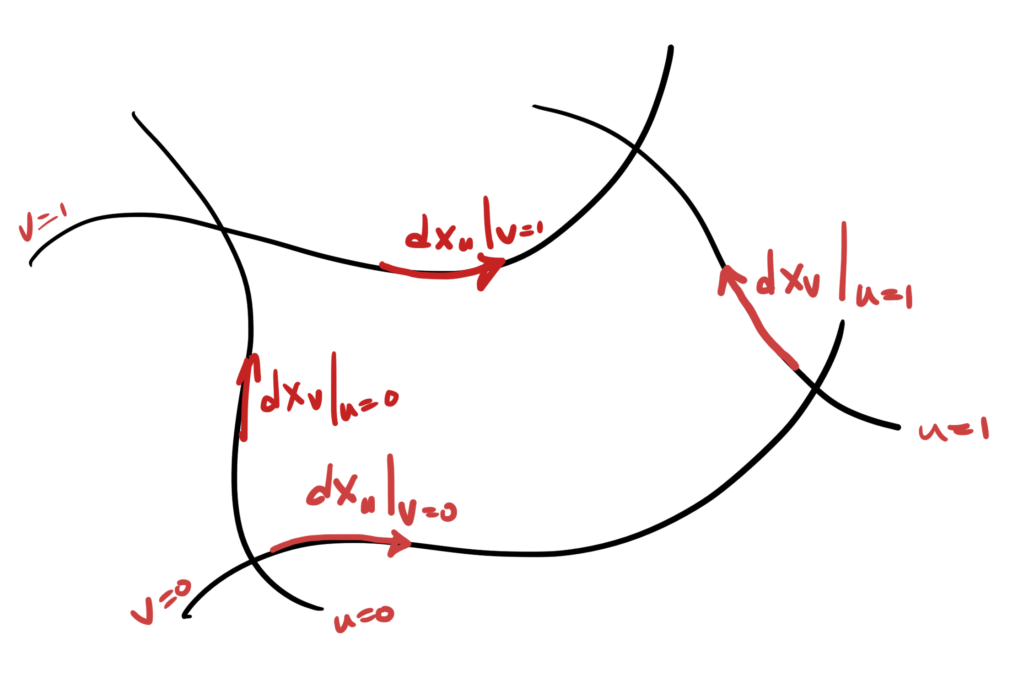
fig. 1. Two parameter manifold.
Our curvilinear coordinates \( \Bx_u, \Bx_v, \Bx_w \) are dual to the reciprocal basis \( \Bx^u, \Bx^v, \Bx^w \), but we won’t actually have to calculate that reciprocal basis. Instead we need only know that it can be calculated and is defined by the relations \( \Bx_a \cdot \Bx^b = \delta_a^b \). Knowing that we can reduce (say),
\begin{equation}\label{eqn:stokesMaxwellSpaceTimeSplit:140}
\begin{aligned}
d^2 \Bx \cdot ( \spacegrad \wedge \BE )
&=
d^2 \Bx \cdot ( \Bx^a \partial_a \wedge \BE ) \\
&=
(\Bx_u \wedge \Bx_v) \cdot ( \Bx^a \wedge \partial_a \BE ) \,du dv \\
&=
(((\Bx_u \wedge \Bx_v) \cdot \Bx^a) \cdot \partial_a \BE \,du dv \\
&=
d\Bx_u \cdot \partial_v \BE \,dv
-d\Bx_v \cdot \partial_u \BE \,du,
\end{aligned}
\end{equation}
Because each of the differentials, for example \( d\Bx_u = (\PDi{u}{\Bx}) du \), is calculated with the other (i.e.\( v \)) held constant, this is directly integrable, leaving
\begin{equation}\label{eqn:stokesMaxwellSpaceTimeSplit:160}
\begin{aligned}
\int d^2 \Bx \cdot ( \spacegrad \wedge \BE )
&=
\int \evalrange{\lr{d\Bx_u \cdot \BE}}{v=0}{v=1}
-\int \evalrange{\lr{d\Bx_v \cdot \BE}}{u=0}{u=1} \\
&=
\oint d\Bx \cdot \BE.
\end{aligned}
\end{equation}
That direct integration of one of the parameters, while the others are held constant, is the basic idea behind Stokes theorem.
The pseudoscalar grade Maxwell’s equations from \ref{eqn:stokesMaxwellSpaceTimeSplit:80} require a three parameter volume element to apply Stokes theorem to. Again, allowing for curvilinear coordinates such a differential expands as
\begin{equation}\label{eqn:stokesMaxwellSpaceTimeSplit:180}
\begin{aligned}
d^3 \Bx \cdot (\spacegrad \wedge (I\BB))
&=
(( \Bx_u \wedge \Bx_v \wedge \Bx_w ) \cdot \Bx^a ) \cdot \partial_a (I\BB) \,du dv dw \\
&=
(d\Bx_u \wedge d\Bx_v) \cdot \partial_w (I\BB) dw
+(d\Bx_v \wedge d\Bx_w) \cdot \partial_u (I\BB) du
+(d\Bx_w \wedge d\Bx_u) \cdot \partial_v (I\BB) dv.
\end{aligned}
\end{equation}
Like the two parameter volume, this is directly integrable
\begin{equation}\label{eqn:stokesMaxwellSpaceTimeSplit:200}
\int
d^3 \Bx \cdot (\spacegrad \wedge (I\BB))
=
\int \evalbar{(d\Bx_u \wedge d\Bx_v) \cdot (I\BB) }{\Delta w}
+\int \evalbar{(d\Bx_v \wedge d\Bx_w) \cdot (I\BB)}{\Delta u}
+\int \evalbar{(d\Bx_w \wedge d\Bx_u) \cdot (I\BB)}{\Delta v}.
\end{equation}
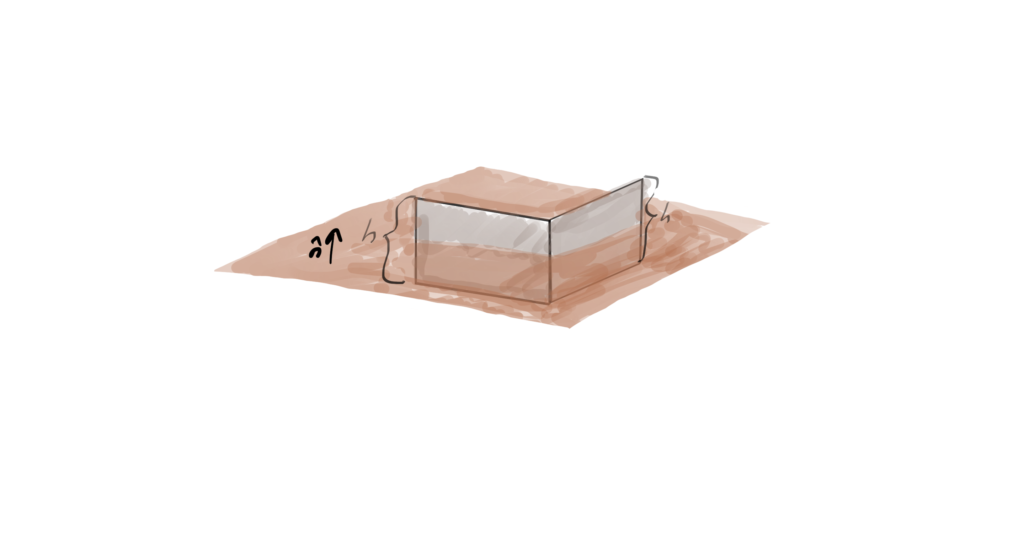
After some thought (or a craft project such as that of fig. 2) is can be observed that this is conceptually an oriented surface integral

fig. 2. Oriented three parameter surface.
Noting that
\begin{equation}\label{eqn:stokesMaxwellSpaceTimeSplit:221}
\begin{aligned}
d^2 \Bx \cdot (I\Bf)
&= \gpgradezero{ d^2 \Bx I B } \\
&= I (d^2\Bx \wedge \Bf)
\end{aligned}
\end{equation}
we can now write down the results of application of Stokes theorem to each of Maxwell’s equations in their curl forms
\begin{equation}\label{eqn:stokesMaxwellSpaceTimeSplit:220}
\boxed{
\begin{aligned}
\oint d\Bx \cdot \BE &= -I \partial_t \int d^2 \Bx \wedge \BB \\
\inv{\mu_0} \oint d\Bx \cdot \BB &= \epsilon_0 I \partial_t \int d^2 \Bx \wedge \BE + I \int d^2 \Bx \wedge \BJ \\
\oint d^2 \Bx \wedge \BE &= \inv{\epsilon_0} \int (d^3 \Bx \cdot I) \rho \\
\oint d^2 \Bx \wedge \BB &= 0.
\end{aligned}
}
\end{equation}
In the three parameter surface integrals the specific meaning to apply to \( d^2 \Bx \wedge \Bf \) is
\begin{equation}\label{eqn:stokesMaxwellSpaceTimeSplit:240}
\oint d^2 \Bx \wedge \Bf
=
\int \evalbar{\lr{d\Bx_u \wedge d\Bx_v \wedge \Bf}}{\Delta w}
+\int \evalbar{\lr{d\Bx_v \wedge d\Bx_w \wedge \Bf}}{\Delta u}
+\int \evalbar{\lr{d\Bx_w \wedge d\Bx_u \wedge \Bf}}{\Delta v}.
\end{equation}
Note that in each case only the component of the vector \( \Bf \) that is projected onto the normal to the area element contributes.
Like this:
Like Loading...