wedge product

Gauge freedom and four-potentials in the STA form of Maxwell’s equation.

March 27, 2022 math and physics play , , , , , , , , , , , , , , , , , , , , ,

[If mathjax doesn’t display properly for you, click here for a PDF of this post]

Motivation.

In a recent video on the tensor structure of Maxwell’s equation, I made a little side trip down the road of potential solutions and gauge transformations. I thought that was worth writing up in text form.

The initial point of that side trip was just to point out that the Faraday tensor can be expressed in terms of four potential coordinates
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:20}
F_{\mu\nu} = \partial_\mu A_\nu – \partial_\nu A_\mu,
\end{equation}
but before I got there I tried to motivate this. In this post, I’ll outline the same ideas.

STA representation of Maxwell’s equation.

We’d gone through the work to show that Maxwell’s equation has the STA form
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:40}
\grad F = J.
\end{equation}
This is a deceptively compact representation, as it requires all of the following definitions
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:60}
\grad = \gamma^\mu \partial_\mu = \gamma_\mu \partial^\mu,
\end{equation}
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:80}
\partial_\mu = \PD{x^\mu}{},
\end{equation}
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:100}
\gamma^\mu \cdot \gamma_\nu = {\delta^\mu}_\nu,
\end{equation}
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:160}
\gamma_\mu \cdot \gamma_\nu = g_{\mu\nu},
\end{equation}
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:120}
\begin{aligned}
F
&= \BE + I c \BB \\
&= -E^k \gamma^k \gamma^0 – \inv{2} c B^r \gamma^s \gamma^t \epsilon^{r s t} \\
&= \inv{2} \gamma^{\mu} \wedge \gamma^{\nu} F_{\mu\nu},
\end{aligned}
\end{equation}
and
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:140}
\begin{aligned}
J &= \gamma_\mu J^\mu \\
J^\mu &= \frac{\rho}{\epsilon} \gamma_0 + \eta (\BJ \cdot \Be_k).
\end{aligned}
\end{equation}

Four-potentials in the STA representation.

In order to find the tensor form of Maxwell’s equation (starting from the STA representation), we first split the equation into two, since
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:180}
\grad F = \grad \cdot F + \grad \wedge F = J.
\end{equation}
The dot product is a four-vector, the wedge term is a trivector, and the current is a four-vector, so we have one grade-1 equation and one grade-3 equation
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:200}
\begin{aligned}
\grad \cdot F &= J \\
\grad \wedge F &= 0.
\end{aligned}
\end{equation}
The potential comes into the mix, since the curl equation above means that \( F \) necessarily can be written as the curl of some four-vector
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:220}
F = \grad \wedge A.
\end{equation}
One justification of this is that \( a \wedge (a \wedge b) = 0 \), for any vectors \( a, b \). Expanding such a double-curl out in coordinates is also worthwhile
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:240}
\begin{aligned}
\grad \wedge \lr{ \grad \wedge A }
&=
\lr{ \gamma_\mu \partial^\mu }
\wedge
\lr{ \gamma_\nu \partial^\nu }
\wedge
A \\
&=
\gamma^\mu \wedge \gamma^\nu \wedge \lr{ \partial_\mu \partial_\nu A }.
\end{aligned}
\end{equation}
Provided we have equality of mixed partials, this is a product of an antisymmetric factor and a symmetric factor, so the full sum is zero.

Things get interesting if one imposes a \( \grad \cdot A = \partial_\mu A^\mu = 0 \) constraint on the potential. If we do so, then
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:260}
\grad F = \grad^2 A = J.
\end{equation}
Observe that \( \grad^2 \) is the wave equation operator (often written as a square-box symbol.) That is
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:280}
\begin{aligned}
\grad^2
&= \partial^\mu \partial_\mu \\
&= \partial_0 \partial_0
– \partial_1 \partial_1
– \partial_2 \partial_2
– \partial_3 \partial_3 \\
&= \inv{c^2} \PDSq{t}{} – \spacegrad^2.
\end{aligned}
\end{equation}
This is also an operator for which the Green’s function is well known ([1]), which means that we can immediately write the solutions
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:300}
A(x) = \int G(x,x’) J(x’) d^4 x’.
\end{equation}
However, we have no a-priori guarantee that such a solution has zero divergence. We can fix that by making a gauge transformation of the form
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:320}
A \rightarrow A – \grad \chi.
\end{equation}
Observe that such a transformation does not change the electromagnetic field
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:340}
F = \grad \wedge A \rightarrow \grad \wedge \lr{ A – \grad \chi },
\end{equation}
since
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:360}
\grad \wedge \grad \chi = 0,
\end{equation}
(also by equality of mixed partials.) Suppose that \( \tilde{A} \) is a solution of \( \grad^2 \tilde{A} = J \), and \( \tilde{A} = A + \grad \chi \), where \( A \) is a zero divergence field to be determined, then
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:380}
\grad \cdot \tilde{A}
=
\grad \cdot A + \grad^2 \chi,
\end{equation}
or
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:400}
\grad^2 \chi = \grad \cdot \tilde{A}.
\end{equation}
So if \( \tilde{A} \) does not have zero divergence, we can find a \( \chi \)
\begin{equation}\label{eqn:gaugeFreedomAndPotentialsMaxwell:420}
\chi(x) = \int G(x,x’) \grad’ \cdot \tilde{A}(x’) d^4 x’,
\end{equation}
so that \( A = \tilde{A} – \grad \chi \) does have zero divergence.

References

[1] JD Jackson. Classical Electrodynamics. John Wiley and Sons, 2nd edition, 1975.

Verifying the GA form for the symmetric and antisymmetric components of the different rate of strain.

March 8, 2022 math and physics play , , , , , , , ,

[If mathjax doesn’t display properly for you, click here for a PDF of this post]

We found geometric algebra representations for the symmetric and antisymmetric components for a gradient-vector direct product. In particular, given
\begin{equation}\label{eqn:tensorComponents:20}
d\Bv = d\Bx \cdot \lr{ \spacegrad \otimes \Bv }
\end{equation}
we found
\begin{equation}\label{eqn:tensorComponents:40}
\begin{aligned}
d\Bx \cdot \Bd
&=
\inv{2} d\Bx \cdot \lr{
\spacegrad \otimes \Bv
+
\lr{\spacegrad \otimes \Bv }^\dagger
} \\
&=
\inv{2} \lr{
d\Bx \lr{ \spacegrad \cdot \Bv }
+
\gpgradeone{ \spacegrad d\Bx \Bv }
},
\end{aligned}
\end{equation}
and
\begin{equation}\label{eqn:tensorComponents:60}
\begin{aligned}
d\Bx \cdot \BOmega
&=
\inv{2} d\Bx \cdot \lr{
\spacegrad \otimes \Bv
–
\lr{\spacegrad \otimes \Bv }^\dagger
} \\
&=
\inv{2} \lr{
d\Bx \lr{ \spacegrad \cdot \Bv }
–
\gpgradeone{ d\Bx \Bv \spacegrad }
}.
\end{aligned}
\end{equation}

Let’s expand each of these in coordinates to verify that these are correct. For the symmetric component, that is
\begin{equation}\label{eqn:tensorComponents:80}
\begin{aligned}
d\Bx \cdot \Bd
&=
\inv{2}
\lr{
dx_i \partial_j v_j \Be_i
+
\partial_j dx_i v_k \gpgradeone{ \Be_j \Be_i \Be_k }
} \\
&=
\inv{2} dx_i
\lr{
\partial_j v_j \Be_i
+
\partial_j v_k \lr{ \delta_{ji} \Be_k + \lr{ \Be_j \wedge \Be_i } \cdot \Be_k }
} \\
&=
\inv{2} dx_i
\lr{
\partial_j v_j \Be_i
+
\partial_j v_k \lr{ \delta_{ji} \Be_k + \delta_{ik} \Be_j – \delta_{jk} \Be_i }
} \\
&=
\inv{2} dx_i
\lr{
\partial_j v_j \Be_i
+
\partial_i v_k \Be_k
+
\partial_j v_i \Be_j
–
\partial_j v_j \Be_i
} \\
&=
\inv{2} dx_i
\lr{
\partial_i v_k \Be_k
+
\partial_j v_i \Be_j
} \\
&=
dx_i \inv{2} \lr{ \partial_i v_j + \partial_j v_i } \Be_j.
\end{aligned}
\end{equation}
Sure enough, we that the product contains the matrix element of the symmetric component of \( \spacegrad \otimes \Bv \).

Now let’s verify that our GA antisymmetric tensor product representation works out.
\begin{equation}\label{eqn:tensorComponents:100}
\begin{aligned}
d\Bx \cdot \BOmega
&=
\inv{2}
\lr{
dx_i \partial_j v_j \Be_i
–
dx_i \partial_k v_j \gpgradeone{ \Be_i \Be_j \Be_k }
} \\
&=
\inv{2} dx_i
\lr{
\partial_j v_j \Be_i
–
\partial_k v_j
\lr{ \delta_{ij} \Be_k + \delta_{jk} \Be_i – \delta_{ik} \Be_j }
} \\
&=
\inv{2} dx_i
\lr{
\partial_j v_j \Be_i
–
\partial_k v_i \Be_k
–
\partial_k v_k \Be_i
+
\partial_i v_j \Be_j
} \\
&=
\inv{2} dx_i
\lr{
\partial_i v_j \Be_j
–
\partial_k v_i \Be_k
} \\
&=
dx_i
\inv{2}
\lr{
\partial_i v_j
–
\partial_j v_i
}
\Be_j.
\end{aligned}
\end{equation}
As expected, we that this product contains the matrix element of the antisymmetric component of \( \spacegrad \otimes \Bv \).

We also found previously that \( \BOmega \) is just a curl, namely
\begin{equation}\label{eqn:tensorComponents:120}
\BOmega = \inv{2} \lr{ \spacegrad \wedge \Bv } = \inv{2} \lr{ \partial_i v_j } \Be_i \wedge \Be_j,
\end{equation}
which directly encodes the antisymmetric component of \( \spacegrad \otimes \Bv \). We can also see that by fully expanding \( d\Bx \cdot \BOmega \), which gives
\begin{equation}\label{eqn:tensorComponents:140}
\begin{aligned}
d\Bx \cdot \BOmega
&=
dx_i \inv{2} \lr{ \partial_j v_k }
\Be_i \cdot \lr{ \Be_j \wedge \Be_k } \\
&=
dx_i \inv{2} \lr{ \partial_j v_k }
\lr{
\delta_{ij} \Be_k
–
\delta_{ik} \Be_j
} \\
&=
dx_i \inv{2}
\lr{
\lr{ \partial_i v_k } \Be_k
–
\lr{ \partial_j v_i }
\Be_j
} \\
&=
dx_i \inv{2}
\lr{
\partial_i v_j – \partial_j v_i
}
\Be_j,
\end{aligned}
\end{equation}
as expected.

Some experiments in youtube mathematics videos

January 3, 2021 math and physics play , , , , , , ,

A couple years ago I was curious how easy it would be to use a graphics tablet as a virtual chalkboard, and produced a handful of very rough YouTube videos to get a feel for the basics of streaming and video editing (much of which I’ve now forgotten how to do). These were the videos in chronological order:

  • Introduction to Geometric (Clifford) Algebra.Introduction to Geometric (Clifford) algebra. Interpretation of products of unit vectors, rules for reducing products of unit vectors, and the axioms that justify those rules.
  • Geometric Algebra: dot, wedge, cross and vector products.Geometric (Clifford) Algebra introduction, showing the relation between the vector product dot and wedge products, and the cross product.
  • Solution of two line intersection using geometric algebra.
  • Linear system solution using the wedge product.. This video provides a standalone introduction to the wedge product, the geometry of the wedge product and some properties, and linear system solution as a sample application. In this video the wedge product is introduced independently of any geometric (Clifford) algebra, as an antisymmetric and associative operator. You’ll see that we get Cramer’s rule for free from this solution technique.
  • Exponential form of vector products in geometric algebra.In this video, I discussed the exponential form of the product of two vectors.

    I showed an example of how two unit vectors, each rotations of zcap orthonormal \(\mathbb{R}^3\) planes, produce a “complex” exponential in the plane that spans these two vectors.

  • Velocity and acceleration in cylindrical coordinates using geometric algebra.I derived the cylindrical coordinate representations of the velocity and acceleration vectors, showing the radial and azimuthal components of each vector.

    I also showed how these are related to the dot and wedge product with the radial unit vector.

  • Duality transformations in geometric algebra.Duality transformations (pseudoscalar multiplication) will be demonstrated in \(\mathbb{R}^2\) and \(\mathbb{R}^3\).

    A polar parameterized vector in \(\mathbb{R}^2\), written in complex exponential form, is multiplied by a unit pseudoscalar for the x-y plane. We see that the result is a vector normal to that vector, with the direction of the normal dependent on the order of multiplication, and the orientation of the pseudoscalar used.

    In \(\mathbb{R}^3\) we see that a vector multiplied by a pseudoscalar yields the bivector that represents the plane that is normal to that vector. The sign of that bivector (or its cyclic orientation) depends on the orientation of the pseudoscalar. The order of multiplication was not mentioned in this case since the \(\mathbb{R}^3\) pseudoscalar commutes with any grade object (assumed, not proved). An example of a vector with two components in a plane, multiplied by a pseudoscalar was also given, which allowed for a visualization of the bivector that is normal to the original vector.

  • Math bait and switch: Fractional integer exponents.When I was a kid, my dad asked me to explain fractional exponents, and perhaps any non-positive integer exponents, to him. He objected to the idea of multiplying something by itself \(1/2\) times.

    I failed to answer the question to his satisfaction. My own son is now reviewing the rules of exponentiation, and it occurred to me (30 years later) why my explanation to Dad failed.

    Essentially, there’s a small bait and switch required, and my dad didn’t fall for it.

    The meaning that my dad gave to exponentiation was that \( x^n\) equals \(x\) times itself \(n\) times.

    Using this rule, it is easy to demonstrate that \(x^a x^b = x^{a + b}\), and this can be used to justify expressions like \(x^{1/2}\). However, doing this really means that we’ve switched the definition of exponential, defining an exponential as any number that satisfies the relationship:

    \(x^a x^b = x^{a+b}\),

    where \(x^1 = x\). This slight of hand is required to give meaning to \(x^{1/2}\) or other exponentials where the exponential argument is any non-positive integer.

Of these videos I just relistened to the wedge product episode, as I had a new lone comment on it, and I couldn’t even remember what I had said. It wasn’t completely horrible, despite the low tech. I was, however, very surprised how soft and gentle my voice was. When I am talking math in person, I get very animated, but attempting to manage the tech was distracting and all the excitement that I’d normally have was obliterated.

I’d love to attempt a manim based presentation of some of this material, but suspect if I do something completely scripted like that, I may not be a very good narrator.

Fundamental theorem of geometric calculus for line integrals (relativistic.)

December 16, 2020 math and physics play , , , , , , , , , , , , , , , , , , , , , , , , , , ,

[This post is best viewed in PDF form, due to latex elements that I could not format with wordpress mathjax.]

Background for this particular post can be found in

  1. Curvilinear coordinates and gradient in spacetime, and reciprocal frames, and
  2. Lorentz transformations in Space Time Algebra (STA)
  3. A couple more reciprocal frame examples.

Motivation.

I’ve been slowly working my way towards a statement of the fundamental theorem of integral calculus, where the functions being integrated are elements of the Dirac algebra (space time multivectors in the geometric algebra parlance.)

This is interesting because we want to be able to do line, surface, 3-volume and 4-volume space time integrals. We have many \(\mathbb{R}^3\) integral theorems
\begin{equation}\label{eqn:fundamentalTheoremOfGC:40a}
\int_A^B d\Bl \cdot \spacegrad f = f(B) – f(A),
\end{equation}
\begin{equation}\label{eqn:fundamentalTheoremOfGC:60a}
\int_S dA\, \ncap \cross \spacegrad f = \int_{\partial S} d\Bx\, f,
\end{equation}
\begin{equation}\label{eqn:fundamentalTheoremOfGC:80a}
\int_S dA\, \ncap \cdot \lr{ \spacegrad \cross \Bf} = \int_{\partial S} d\Bx \cdot \Bf,
\end{equation}
\begin{equation}\label{eqn:fundamentalTheoremOfGC:100a}
\int_S dx dy \lr{ \PD{y}{P} – \PD{x}{Q} }
=
\int_{\partial S} P dx + Q dy,
\end{equation}
\begin{equation}\label{eqn:fundamentalTheoremOfGC:120a}
\int_V dV\, \spacegrad f = \int_{\partial V} dA\, \ncap f,
\end{equation}
\begin{equation}\label{eqn:fundamentalTheoremOfGC:140a}
\int_V dV\, \spacegrad \cross \Bf = \int_{\partial V} dA\, \ncap \cross \Bf,
\end{equation}
\begin{equation}\label{eqn:fundamentalTheoremOfGC:160a}
\int_V dV\, \spacegrad \cdot \Bf = \int_{\partial V} dA\, \ncap \cdot \Bf,
\end{equation}
and want to know how to generalize these to four dimensions and also make sure that we are handling the relativistic mixed signature correctly. If our starting point was the mess of equations above, we’d be in trouble, since it is not obvious how these generalize. All the theorems with unit normals have to be handled completely differently in four dimensions since we don’t have a unique normal to any given spacetime plane.
What comes to our rescue is the Fundamental Theorem of Geometric Calculus (FTGC), which has the form
\begin{equation}\label{eqn:fundamentalTheoremOfGC:40}
\int F d^n \Bx\, \lrpartial G = \int F d^{n-1} \Bx\, G,
\end{equation}
where \(F,G\) are multivectors functions (i.e. sums of products of vectors.) We’ve seen ([2], [1]) that all the identities above are special cases of the fundamental theorem.

Do we need any special care to state the FTGC correctly for our relativistic case? It turns out that the answer is no! Tangent and reciprocal frame vectors do all the heavy lifting, and we can use the fundamental theorem as is, even in our mixed signature space. The only real change that we need to make is use spacetime gradient and vector derivative operators instead of their spatial equivalents. We will see how this works below. Note that instead of starting with \ref{eqn:fundamentalTheoremOfGC:40} directly, I will attempt to build up to that point in a progressive fashion that is hopefully does not require the reader to make too many unjustified mental leaps.

Multivector line integrals.

We want to define multivector line integrals to start with. Recall that in \(\mathbb{R}^3\) we would say that for scalar functions \( f\), the integral
\begin{equation}\label{eqn:fundamentalTheoremOfGC:180b}
\int d\Bx\, f = \int f d\Bx,
\end{equation}
is a line integral. Also, for vector functions \( \Bf \) we call
\begin{equation}\label{eqn:fundamentalTheoremOfGC:200}
\int d\Bx \cdot \Bf = \inv{2} \int d\Bx\, \Bf + \Bf d\Bx.
\end{equation}
a line integral. In order to generalize line integrals to multivector functions, we will allow our multivector functions to be placed on either or both sides of the differential.

Definition 1.1: Line integral.

Given a single variable parameterization \( x = x(u) \), we write \( d^1\Bx = \Bx_u du \), and call
\begin{equation}\label{eqn:fundamentalTheoremOfGC:220a}
\int F d^1\Bx\, G,
\end{equation}
a line integral, where \( F,G \) are arbitrary multivector functions.

We must be careful not to reorder any of the factors in the integrand, since the differential may not commute with either \( F \) or \( G \). Here is a simple example where the integrand has a product of a vector and differential.

Problem: Circular parameterization.

Given a circular parameterization \( x(\theta) = \gamma_1 e^{-i\theta} \), where \( i = \gamma_1 \gamma_2 \), the unit bivector for the \(x,y\) plane. Compute the line integral
\begin{equation}\label{eqn:fundamentalTheoremOfGC:100}
\int_0^{\pi/4} F(\theta)\, d^1 \Bx\, G(\theta),
\end{equation}
where \( F(\theta) = \Bx^\theta + \gamma_3 + \gamma_1 \gamma_0 \) is a multivector valued function, and \( G(\theta) = \gamma_0 \) is vector valued.

Answer

The tangent vector for the curve is
\begin{equation}\label{eqn:fundamentalTheoremOfGC:60}
\Bx_\theta
= -\gamma_1 \gamma_1 \gamma_2 e^{-i\theta}
= \gamma_2 e^{-i\theta},
\end{equation}
with reciprocal vector \( \Bx^\theta = e^{i \theta} \gamma^2 \). The differential element is \( d^1 \Bx = \gamma_2 e^{-i\theta} d\theta \), so the integrand is
\begin{equation}\label{eqn:fundamentalTheoremOfGC:80}
\begin{aligned}
\int_0^{\pi/4} \lr{ \Bx^\theta + \gamma_3 + \gamma_1 \gamma_0 } d^1 \Bx\, \gamma_0
&=
\int_0^{\pi/4} \lr{ e^{i\theta} \gamma^2 + \gamma_3 + \gamma_1 \gamma_0 } \gamma_2 e^{-i\theta} d\theta\, \gamma_0 \\
&=
\frac{\pi}{4} \gamma_0 + \lr{ \gamma_{32} + \gamma_{102} } \inv{-i} \lr{ e^{-i\pi/4} – 1 } \gamma_0 \\
&=
\frac{\pi}{4} \gamma_0 + \inv{\sqrt{2}} \lr{ \gamma_{32} + \gamma_{102} } \gamma_{120} \lr{ 1 – \gamma_{12} } \\
&=
\frac{\pi}{4} \gamma_0 + \inv{\sqrt{2}} \lr{ \gamma_{310} + 1 } \lr{ 1 – \gamma_{12} }.
\end{aligned}
\end{equation}
Observe how care is required not to reorder any terms. This particular end result is a multivector with scalar, vector, bivector, and trivector grades, but no pseudoscalar component. The grades in the end result depend on both the function in the integrand and on the path. For example, had we integrated all the way around the circle, the end result would have been the vector \( 2 \pi \gamma_0 \) (i.e. a \( \gamma_0 \) weighted unit circle circumference), as all the other grades would have been killed by the complex exponential integrated over a full period.

Problem: Line integral for boosted time direction vector.

Let \( x = e^{\vcap \alpha/2} \gamma_0 e^{-\vcap \alpha/2} \) represent the spacetime curve of all the boosts of \( \gamma_0 \) along a specific velocity direction vector, where \( \vcap = (v \wedge \gamma_0)/\Norm{v \wedge \gamma_0} \) is a unit spatial bivector for any constant vector \( v \). Compute the line integral
\begin{equation}\label{eqn:fundamentalTheoremOfGC:240}
\int x\, d^1 \Bx.
\end{equation}

Answer

Observe that \( \vcap \) and \( \gamma_0 \) anticommute, so we may write our boost as a one sided exponential
\begin{equation}\label{eqn:fundamentalTheoremOfGC:260}
x(\alpha) = \gamma_0 e^{-\vcap \alpha} = e^{\vcap \alpha} \gamma_0 = \lr{ \cosh\alpha + \vcap \sinh\alpha } \gamma_0.
\end{equation}
The tangent vector is just
\begin{equation}\label{eqn:fundamentalTheoremOfGC:280}
\Bx_\alpha = \PD{\alpha}{x} = e^{\vcap\alpha} \vcap \gamma_0.
\end{equation}
Let’s get a bit of intuition about the nature of this vector. It’s square is
\begin{equation}\label{eqn:fundamentalTheoremOfGC:300}
\begin{aligned}
\Bx_\alpha^2
&=
e^{\vcap\alpha} \vcap \gamma_0
e^{\vcap\alpha} \vcap \gamma_0 \\
&=
-e^{\vcap\alpha} \vcap e^{-\vcap\alpha} \vcap (\gamma_0)^2 \\
&=
-1,
\end{aligned}
\end{equation}
so we see that the tangent vector is a spacelike unit vector. As the vector representing points on the curve is necessarily timelike (due to Lorentz invariance), these two must be orthogonal at all points. Let’s confirm this algebraically
\begin{equation}\label{eqn:fundamentalTheoremOfGC:320}
\begin{aligned}
x \cdot \Bx_\alpha
&=
\gpgradezero{ e^{\vcap \alpha} \gamma_0 e^{\vcap \alpha} \vcap \gamma_0 } \\
&=
\gpgradezero{ e^{-\vcap \alpha} e^{\vcap \alpha} \vcap (\gamma_0)^2 } \\
&=
\gpgradezero{ \vcap } \\
&= 0.
\end{aligned}
\end{equation}
Here we used \( e^{\vcap \alpha} \gamma_0 = \gamma_0 e^{-\vcap \alpha} \), and \( \gpgradezero{A B} = \gpgradezero{B A} \). Geometrically, we have the curious fact that the direction vectors to points on the curve are perpendicular (with respect to our relativistic dot product) to the tangent vectors on the curve, as illustrated in fig. 1.

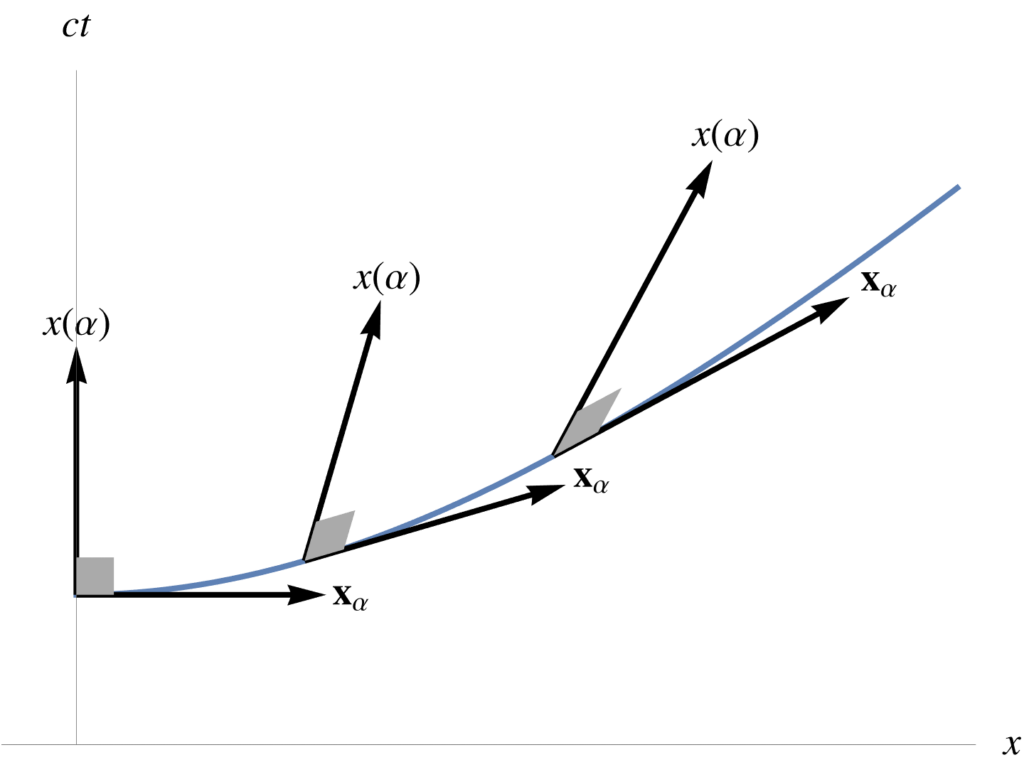
fig. 1. Tangent perpendicularity in mixed metric.

Perfect differentials.

Having seen a couple examples of multivector line integrals, let’s now move on to figure out the structure of a line integral that has a “perfect” differential integrand. We can take a hint from the \(\mathbb{R}^3\) vector result that we already know, namely
\begin{equation}\label{eqn:fundamentalTheoremOfGC:120}
\int_A^B d\Bl \cdot \spacegrad f = f(B) – f(A).
\end{equation}
It seems reasonable to guess that the relativistic generalization of this is
\begin{equation}\label{eqn:fundamentalTheoremOfGC:140}
\int_A^B dx \cdot \grad f = f(B) – f(A).
\end{equation}
Let’s check that, by expanding in coordinates
\begin{equation}\label{eqn:fundamentalTheoremOfGC:160}
\begin{aligned}
\int_A^B dx \cdot \grad f
&=
\int_A^B d\tau \frac{dx^\mu}{d\tau} \partial_\mu f \\
&=
\int_A^B d\tau \frac{dx^\mu}{d\tau} \PD{x^\mu}{f} \\
&=
\int_A^B d\tau \frac{df}{d\tau} \\
&=
f(B) – f(A).
\end{aligned}
\end{equation}
If we drop the dot product, will we have such a nice result? Let’s see:
\begin{equation}\label{eqn:fundamentalTheoremOfGC:180}
\begin{aligned}
\int_A^B dx \grad f
&=
\int_A^B d\tau \frac{dx^\mu}{d\tau} \gamma_\mu \gamma^\nu \partial_\nu f \\
&=
\int_A^B d\tau \frac{dx^\mu}{d\tau} \PD{x^\mu}{f}
+
\int_A^B
d\tau
\sum_{\mu \ne \nu} \gamma_\mu \gamma^\nu
\frac{dx^\mu}{d\tau} \PD{x^\nu}{f}.
\end{aligned}
\end{equation}
This scalar component of this integrand is a perfect differential, but the bivector part of the integrand is a complete mess, that we have no hope of generally integrating. It happens that if we consider one of the simplest parameterization examples, we can get a strong hint of how to generalize the differential operator to one that ends up providing a perfect differential. In particular, let’s integrate over a linear constant path, such as \( x(\tau) = \tau \gamma_0 \). For this path, we have
\begin{equation}\label{eqn:fundamentalTheoremOfGC:200a}
\begin{aligned}
\int_A^B dx \grad f
&=
\int_A^B \gamma_0 d\tau \lr{
\gamma^0 \partial_0 +
\gamma^1 \partial_1 +
\gamma^2 \partial_2 +
\gamma^3 \partial_3 } f \\
&=
\int_A^B d\tau \lr{
\PD{\tau}{f} +
\gamma_0 \gamma^1 \PD{x^1}{f} +
\gamma_0 \gamma^2 \PD{x^2}{f} +
\gamma_0 \gamma^3 \PD{x^3}{f}
}.
\end{aligned}
\end{equation}
Just because the path does not have any \( x^1, x^2, x^3 \) component dependencies does not mean that these last three partials are neccessarily zero. For example \( f = f(x(\tau)) = \lr{ x^0 }^2 \gamma_0 + x^1 \gamma_1 \) will have a non-zero contribution from the \( \partial_1 \) operator. In that particular case, we can easily integrate \( f \), but we have to know the specifics of the function to do the integral. However, if we had a differential operator that did not include any component off the integration path, we would ahve a perfect differential. That is, if we were to replace the gradient with the projection of the gradient onto the tangent space, we would have a perfect differential. We see that the function of the dot product in \ref{eqn:fundamentalTheoremOfGC:140} has the same effect, as it rejects any component of the gradient that does not lie on the tangent space.

Definition 1.2: Vector derivative.

Given a spacetime manifold parameterized by \( x = x(u^0, \cdots u^{N-1}) \), with tangent vectors \( \Bx_\mu = \PDi{u^\mu}{x} \), and reciprocal vectors \( \Bx^\mu \in \textrm{Span}\setlr{\Bx_\nu} \), such that \( \Bx^\mu \cdot \Bx_\nu = {\delta^\mu}_\nu \), the vector derivative is defined as
\begin{equation}\label{eqn:fundamentalTheoremOfGC:240a}
\partial = \sum_{\mu = 0}^{N-1} \Bx^\mu \PD{u^\mu}{}.
\end{equation}
Observe that if this is a full parameterization of the space (\(N = 4\)), then the vector derivative is identical to the gradient. The vector derivative is the projection of the gradient onto the tangent space at the point of evaluation.Furthermore, we designate \( \lrpartial \) as the vector derivative allowed to act bidirectionally, as follows
\begin{equation}\label{eqn:fundamentalTheoremOfGC:260a}
R \lrpartial S
=
R \Bx^\mu \PD{u^\mu}{S}
+
\PD{u^\mu}{R} \Bx^\mu S,
\end{equation}
where \( R, S \) are multivectors, and summation convention is implied. In this bidirectional action,
the vector factors of the vector derivative must stay in place (as they do not neccessarily commute with \( R,S\)), but the derivative operators apply in a chain rule like fashion to both functions.

Noting that \( \Bx_u \cdot \grad = \Bx_u \cdot \partial \), we may rewrite the scalar line integral identity \ref{eqn:fundamentalTheoremOfGC:140} as
\begin{equation}\label{eqn:fundamentalTheoremOfGC:220}
\int_A^B dx \cdot \partial f = f(B) – f(A).
\end{equation}
However, as our example hinted at, the fundamental theorem for line integrals has a multivector generalization that does not rely on a dot product to do the tangent space filtering, and is more powerful. That generalization has the following form.

Theorem 1.1: Fundamental theorem for line integrals.

Given multivector functions \( F, G \), and a single parameter curve \( x(u) \) with line element \( d^1 \Bx = \Bx_u du \), then
\begin{equation}\label{eqn:fundamentalTheoremOfGC:280a}
\int_A^B F d^1\Bx \lrpartial G = F(B) G(B) – F(A) G(A).
\end{equation}

Start proof:

Writing out the integrand explicitly, we find
\begin{equation}\label{eqn:fundamentalTheoremOfGC:340}
\int_A^B F d^1\Bx \lrpartial G
=
\int_A^B \lr{
\PD{\alpha}{F} d\alpha\, \Bx_\alpha \Bx^\alpha G
+
F d\alpha\, \Bx_\alpha \Bx^\alpha \PD{\alpha}{G }
}
\end{equation}
However for a single parameter curve, we have \( \Bx^\alpha = 1/\Bx_\alpha \), so we are left with
\begin{equation}\label{eqn:fundamentalTheoremOfGC:360}
\begin{aligned}
\int_A^B F d^1\Bx \lrpartial G
&=
\int_A^B d\alpha\, \PD{\alpha}{(F G)} \\
&=
\evalbar{F G}{B}
–
\evalbar{F G}{A}.
\end{aligned}
\end{equation}

End proof.

More to come.

In the next installment we will explore surface integrals in spacetime, and the generalization of the fundamental theorem to multivector space time integrals.

References

[1] Peeter Joot. Geometric Algebra for Electrical Engineers. Kindle Direct Publishing, 2019.

[2] A. Macdonald. Vector and Geometric Calculus. CreateSpace Independent Publishing Platform, 2012.

Lorentz transformations in Space Time Algebra (STA)

December 12, 2020 math and physics play , , , , , , , , , , , , , , , , , ,

[If mathjax doesn’t display properly for you, click here for a PDF of this post]

Motivation.

One of the remarkable features of geometric algebra are the complex exponential sandwiches that can be used to encode rotations in any dimension, or rotation like operations like Lorentz transformations in Minkowski spaces. In this post, we show some examples that unpack the geometric algebra expressions for Lorentz transformations operations of this sort. In particular, we will look at the exponential sandwich operations for spatial rotations and Lorentz boosts in the Dirac algebra, known as Space Time Algebra (STA) in geometric algebra circles, and demonstrate that these sandwiches do have the desired effects.

Lorentz transformations.

Theorem 1.1: Lorentz transformation.

The transformation
\begin{equation}\label{eqn:lorentzTransform:580}
x \rightarrow e^{B} x e^{-B} = x’,
\end{equation}
where \( B = a \wedge b \), is an STA 2-blade for any two linearly independent four-vectors \( a, b \), is a norm preserving, that is
\begin{equation}\label{eqn:lorentzTransform:600}
x^2 = {x’}^2.
\end{equation}

Start proof:

The proof is disturbingly trivial in this geometric algebra form
\begin{equation}\label{eqn:lorentzTransform:40}
\begin{aligned}
{x’}^2
&=
e^{B} x e^{-B} e^{B} x e^{-B} \\
&=
e^{B} x x e^{-B} \\
&=
x^2 e^{B} e^{-B} \\
&=
x^2.
\end{aligned}
\end{equation}

End proof.

In particular, observe that we did not need to construct the usual infinitesimal representations of rotation and boost transformation matrices or tensors in order to demonstrate that we have spacetime invariance for the transformations. The rough idea of such a transformation is that the exponential commutes with components of the four-vector that lie off the spacetime plane specified by the bivector \( B \), and anticommutes with components of the four-vector that lie in the plane. The end result is that the sandwich operation simplifies to
\begin{equation}\label{eqn:lorentzTransform:60}
x’ = x_\parallel e^{-B} + x_\perp,
\end{equation}
where \( x = x_\perp + x_\parallel \) and \( x_\perp \cdot B = 0 \), and \( x_\parallel \wedge B = 0 \). In particular, using \( x = x B B^{-1} = \lr{ x \cdot B + x \wedge B } B^{-1} \), we find that
\begin{equation}\label{eqn:lorentzTransform:80}
\begin{aligned}
x_\parallel &= \lr{ x \cdot B } B^{-1} \\
x_\perp &= \lr{ x \wedge B } B^{-1}.
\end{aligned}
\end{equation}
When \( B \) is a spacetime plane \( B = b \wedge \gamma_0 \), then this exponential has a hyperbolic nature, and we end up with a Lorentz boost. When \( B \) is a spatial bivector, we end up with a single complex exponential, encoding our plane old 3D rotation. More general \( B \)’s that encode composite boosts and rotations are also possible, but \( B \) must be invertible (it should have no lightlike factors.) The rough geometry of these projections is illustrated in fig 1, where the spacetime plane is represented by \( B \).

Projection and rejection geometry.

fig 1. Projection and rejection geometry.

 

What is not so obvious is how to pick \( B \)’s that correspond to specific rotation axes or boost directions. Let’s consider each of those cases in turn.

Theorem 1.2: Boost.

The boost along a direction vector \( \vcap \) and rapidity \( \alpha \) is given by
\begin{equation}\label{eqn:lorentzTransform:620}
x’ = e^{-\vcap \alpha/2} x e^{\vcap \alpha/2},
\end{equation}
where \( \vcap = \gamma_{k0} \cos\theta^k \) is an STA bivector representing a spatial direction with direction cosines \( \cos\theta^k \).

Start proof:

We want to demonstrate that this is equivalent to the usual boost formulation. We can start with decomposition of the four-vector \( x \) into components that lie in and off of the spacetime plane \( \vcap \).
\begin{equation}\label{eqn:lorentzTransform:100}
\begin{aligned}
x
&= \lr{ x^0 + \Bx } \gamma_0 \\
&= \lr{ x^0 + \Bx \vcap^2 } \gamma_0 \\
&= \lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap + \lr{ \Bx \wedge \vcap} \vcap } \gamma_0,
\end{aligned}
\end{equation}
where \( \Bx = x \wedge \gamma_0 \). The first two components lie in the boost plane, whereas the last is the spatial component of the vector that lies perpendicular to the boost plane. Observe that \( \vcap \) anticommutes with the dot product term and commutes with he wedge product term, so we have
\begin{equation}\label{eqn:lorentzTransform:120}
\begin{aligned}
x’
&=
\lr{ x^0 + \lr{ \Bx \cdot \vcap } \vcap } \gamma_0
e^{\vcap \alpha/2 }
e^{\vcap \alpha/2 }
+
\lr{ \Bx \wedge \vcap } \vcap \gamma_0
e^{-\vcap \alpha/2 }
e^{\vcap \alpha/2 } \\
&=
\lr{ x^0 + \lr{ \Bx \cdot \vcap } \vcap } \gamma_0
e^{\vcap \alpha }
+
\lr{ \Bx \wedge \vcap } \vcap \gamma_0.
\end{aligned}
\end{equation}
Noting that \( \vcap^2 = 1 \), we may expand the exponential in hyperbolic functions, and find that the boosted portion of the vector expands as
\begin{equation}\label{eqn:lorentzTransform:260}
\begin{aligned}
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \gamma_0 e^{\vcap \alpha}
&=
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \gamma_0 \lr{ \cosh\alpha + \vcap \sinh \alpha} \\
&=
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \lr{ \cosh\alpha – \vcap \sinh \alpha} \gamma_0 \\
&=
\lr{ x^0 \cosh\alpha – \lr{ \Bx \cdot \vcap} \sinh \alpha} \gamma_0
+
\lr{ -x^0 \sinh \alpha + \lr{ \Bx \cdot \vcap} \cosh \alpha } \vcap \gamma_0.
\end{aligned}
\end{equation}
We are left with
\begin{equation}\label{eqn:lorentzTransform:320}
\begin{aligned}
x’
&=
\lr{ x^0 \cosh\alpha – \lr{ \Bx \cdot \vcap} \sinh \alpha} \gamma_0
+
\lr{ \lr{ \Bx \cdot \vcap} \cosh \alpha -x^0 \sinh \alpha } \vcap \gamma_0
+
\lr{ \Bx \wedge \vcap} \vcap \gamma_0 \\
&=
\begin{bmatrix}
\gamma_0 & \vcap \gamma_0
\end{bmatrix}
\begin{bmatrix}
\cosh\alpha & – \sinh\alpha \\
-\sinh\alpha & \cosh\alpha
\end{bmatrix}
\begin{bmatrix}
x^0 \\
\Bx \cdot \vcap
\end{bmatrix}
+
\lr{ \Bx \wedge \vcap} \vcap \gamma_0,
\end{aligned}
\end{equation}
which has the desired Lorentz boost structure. Of course, this is usually seen with \( \vcap = \gamma_{10} \) so that the components in the coordinate column vector are \( (ct, x) \).

End proof.

Theorem 1.3: Spatial rotation.

Given two linearly independent spatial bivectors \( \Ba = a^k \gamma_{k0}, \Bb = b^k \gamma_{k0} \), a rotation of \(\theta\) radians in the plane of \( \Ba, \Bb \) from \( \Ba \) towards \( \Bb \), is given by
\begin{equation}\label{eqn:lorentzTransform:640}
x’ = e^{-i\theta} x e^{i\theta},
\end{equation}
where \( i = (\Ba \wedge \Bb)/\Abs{\Ba \wedge \Bb} \), is a unit (spatial) bivector.

Start proof:

Without loss of generality, we may pick \( i = \acap \bcap \), where \( \acap^2 = \bcap^2 = 1 \), and \( \acap \cdot \bcap = 0 \). With such an orthonormal basis for the plane, we can decompose our four vector into portions that lie in and off the plane
\begin{equation}\label{eqn:lorentzTransform:400}
\begin{aligned}
x
&= \lr{ x^0 + \Bx } \gamma_0 \\
&= \lr{ x^0 + \Bx i i^{-1} } \gamma_0 \\
&= \lr{ x^0 + \lr{ \Bx \cdot i } i^{-1} + \lr{ \Bx \wedge i } i^{-1} } \gamma_0.
\end{aligned}
\end{equation}
The projective term lies in the plane of rotation, whereas the timelike and spatial rejection term are perpendicular. That is
\begin{equation}\label{eqn:lorentzTransform:420}
\begin{aligned}
x_\parallel &= \lr{ \Bx \cdot i } i^{-1} \gamma_0 \\
x_\perp &= \lr{ x^0 + \lr{ \Bx \wedge i } i^{-1} } \gamma_0,
\end{aligned}
\end{equation}
where \( x_\parallel \wedge i = 0 \), and \( x_\perp \cdot i = 0 \). The plane pseudoscalar \( i \) anticommutes with \( x_\parallel \), and commutes with \( x_\perp \), so
\begin{equation}\label{eqn:lorentzTransform:440}
\begin{aligned}
x’
&= e^{-i\theta/2} \lr{ x_\parallel + x_\perp } e^{i\theta/2} \\
&= x_\parallel e^{i\theta} + x_\perp.
\end{aligned}
\end{equation}
However
\begin{equation}\label{eqn:lorentzTransform:460}
\begin{aligned}
\lr{ \Bx \cdot i } i^{-1}
&=
\lr{ \Bx \cdot \lr{ \acap \wedge \bcap } } \bcap \acap \\
&=
\lr{\Bx \cdot \acap} \bcap \bcap \acap
-\lr{\Bx \cdot \bcap} \acap \bcap \acap \\
&=
\lr{\Bx \cdot \acap} \acap
+\lr{\Bx \cdot \bcap} \bcap,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:lorentzTransform:480}
\begin{aligned}
x_\parallel e^{i\theta}
&=
\lr{
\lr{\Bx \cdot \acap} \acap
+
\lr{\Bx \cdot \bcap} \bcap
}
\gamma_0
\lr{
\cos\theta + \acap \bcap \sin\theta
} \\
&=
\acap \lr{
\lr{\Bx \cdot \acap} \cos\theta
–
\lr{\Bx \cdot \bcap} \sin\theta
}
\gamma_0
+
\bcap \lr{
\lr{\Bx \cdot \acap} \sin\theta
+
\lr{\Bx \cdot \bcap} \cos\theta
}
\gamma_0,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:lorentzTransform:500}
x’
=
\begin{bmatrix}
\acap & \bcap
\end{bmatrix}
\begin{bmatrix}
\cos\theta & – \sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}
\begin{bmatrix}
\Bx \cdot \acap \\
\Bx \cdot \bcap \\
\end{bmatrix}
\gamma_0
+
\lr{ x \wedge i} i^{-1} \gamma_0.
\end{equation}
Observe that this rejection term can be explicitly expanded to
\begin{equation}\label{eqn:lorentzTransform:520}
\lr{ \Bx \wedge i} i^{-1} \gamma_0 =
x –
\lr{ \Bx \cdot \acap } \acap \gamma_0
–
\lr{ \Bx \cdot \acap } \acap \gamma_0.
\end{equation}
This is the timelike component of the vector, plus the spatial component that is normal to the plane. This exponential sandwich transformation rotates only the portion of the vector that lies in the plane, and leaves the rest (timelike and normal) untouched.

End proof.

Problems.

Problem: Verify components relative to boost direction.

In the proof of thm. 1.2, the vector \( x \) was expanded in terms of the spacetime split. An alternate approach, is to expand as
\begin{equation}\label{eqn:lorentzTransform:340}
\begin{aligned}
x
&= x \vcap^2 \\
&= \lr{ x \cdot \vcap + x \wedge \vcap } \vcap \\
&= \lr{ x \cdot \vcap } \vcap + \lr{ x \wedge \vcap } \vcap.
\end{aligned}
\end{equation}
Show that
\begin{equation}\label{eqn:lorentzTransform:360}
\lr{ x \cdot \vcap } \vcap
=
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \gamma_0,
\end{equation}
and
\begin{equation}\label{eqn:lorentzTransform:380}
\lr{ x \wedge \vcap } \vcap
=
\lr{ \Bx \wedge \vcap} \vcap \gamma_0.
\end{equation}

Answer

Let \( x = x^\mu \gamma_\mu \), so that
\begin{equation}\label{eqn:lorentzTransform:160}
\begin{aligned}
x \cdot \vcap
&=
\gpgradeone{ x^\mu \gamma_\mu \cos\theta^b \gamma_{b 0} } \\
&=
x^\mu \cos\theta^b \gpgradeone{ \gamma_\mu \gamma_{b 0} }
.
\end{aligned}
\end{equation}
The \( \mu = 0 \) component of this grade selection is
\begin{equation}\label{eqn:lorentzTransform:180}
\gpgradeone{ \gamma_0 \gamma_{b 0} }
=
-\gamma_b,
\end{equation}
and for \( \mu = a \ne 0 \), we have
\begin{equation}\label{eqn:lorentzTransform:200}
\gpgradeone{ \gamma_a \gamma_{b 0} }
=
-\delta_{a b} \gamma_0,
\end{equation}
so we have
\begin{equation}\label{eqn:lorentzTransform:220}
\begin{aligned}
x \cdot \vcap
&=
x^0 \cos\theta^b (-\gamma_b)
+
x^a \cos\theta^b (-\delta_{ab} \gamma_0 ) \\
&=
-x^0 \vcap \gamma_0
–
x^b \cos\theta^b \gamma_0 \\
&=
– \lr{ x^0 \vcap + \Bx \cdot \vcap } \gamma_0,
\end{aligned}
\end{equation}
where \( \Bx = x \wedge \gamma_0 \) is the spatial portion of the four vector \( x \) relative to the stationary observer frame. Since \( \vcap \) anticommutes with \( \gamma_0 \), the component of \( x \) in the spacetime plane \( \vcap \) is
\begin{equation}\label{eqn:lorentzTransform:240}
\lr{ x \cdot \vcap } \vcap =
\lr{ x^0 + \lr{ \Bx \cdot \vcap} \vcap } \gamma_0,
\end{equation}
as expected.

For the rejection term, we have
\begin{equation}\label{eqn:lorentzTransform:280}
x \wedge \vcap
=
x^\mu \cos\theta^s \gpgradethree{ \gamma_\mu \gamma_{s 0} }.
\end{equation}
The \( \mu = 0 \) term clearly contributes nothing, leaving us with:
\begin{equation}\label{eqn:lorentzTransform:300}
\begin{aligned}
\lr{ x \wedge \vcap } \vcap
&=
\lr{ x \wedge \vcap } \cdot \vcap \\
&=
x^r \cos\theta^s \cos\theta^t \lr{ \lr{ \gamma_r \wedge \gamma_{s}} \gamma_0 } \cdot \lr{ \gamma_{t0} } \\
&=
x^r \cos\theta^s \cos\theta^t \gpgradeone{
\lr{ \gamma_r \wedge \gamma_{s} } \gamma_0 \gamma_{t0}
} \\
&=
-x^r \cos\theta^s \cos\theta^t \lr{ \gamma_r \wedge \gamma_{s}} \cdot \gamma_t \\
&=
-x^r \cos\theta^s \cos\theta^t \lr{ -\gamma_r \delta_{st} + \gamma_s \delta_{rt} } \\
&=
x^r \cos\theta^t \cos\theta^t \gamma_r
–
x^t \cos\theta^s \cos\theta^t \gamma_s \\
&=
\Bx \gamma_0
– (\Bx \cdot \vcap) \vcap \gamma_0 \\
&=
\lr{ \Bx \wedge \vcap} \vcap \gamma_0,
\end{aligned}
\end{equation}
as expected. Is there a clever way to demonstrate this without resorting to coordinates?

Problem: Rotation transformation components.

Given a unit spatial bivector \( i = \acap \bcap \), where \( \acap \cdot \bcap = 0 \) and \( i^2 = -1 \), show that
\begin{equation}\label{eqn:lorentzTransform:540}
\lr{ x \cdot i } i^{-1}
=
\lr{ \Bx \cdot i } i^{-1} \gamma_0
=
\lr{\Bx \cdot \acap } \acap \gamma_0
+
\lr{\Bx \cdot \bcap } \bcap \gamma_0,
\end{equation}
and
\begin{equation}\label{eqn:lorentzTransform:560}
\lr{ x \wedge i } i^{-1}
=
\lr{ \Bx \wedge i } i^{-1} \gamma_0
=
x –
\lr{\Bx \cdot \acap } \acap \gamma_0
–
\lr{\Bx \cdot \bcap } \bcap \gamma_0.
\end{equation}
Also show that \( i \) anticommutes with \( \lr{ x \cdot i } i^{-1} \) and commutes with \( \lr{ x \wedge i } i^{-1} \).

Answer

This problem is left for the reader, as I don’t feel like typing out my solution.

The first part of this problem can be done in the tedious coordinate approach used above, but hopefully there is a better way.

For the last (commutation) part of the problem, here is a hint. Let \( x \wedge i = n i \), where \( n \cdot i = 0 \). The result then follows easily.