phy1520

PHY1520H Graduate Quantum Mechanics. Lecture 16: Addition of angular momenta. Taught by Prof. Arun Paramekanti

November 17, 2015 phy1520 , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course PHY1520, Graduate Quantum Mechanics, taught by Prof. Paramekanti, covering [1] chap. 3 content.

Addition of angular momenta

  • For orbital angular momentum

    \begin{equation}\label{eqn:qmLecture16:20}
    \begin{aligned}
    \hat{\BL}_1 &= \hat{\Br}_1 \cross \hat{\Bp}_1 \\
    \hat{\BL}_1 &= \hat{\Br}_1 \cross \hat{\Bp}_1,
    \end{aligned}
    \end{equation}

    We can show that it is true that

    \begin{equation}\label{eqn:qmLecture16:40}
    \antisymmetric{L_{1i} + L_{2i}}{L_{1j} + L_{2j}} =
    i \Hbar \epsilon_{i j k} \lr{ L_{1k} + L_{2k} },
    \end{equation}

    because the angular momentum of the independent particles commute. Given this is it fair to consider that the sum

    \begin{equation}\label{eqn:qmLecture16:60}
    \hat{\BL}_1 + \hat{\BL}_2
    \end{equation}

    is also angular momentum.

  • Given \( \ket{l_1, m_1} \) and \( \ket{l_2, m_2} \), if a measurement is made of \( \hat{\BL}_1 + \hat{\BL}_2 \), what do we get?

    Specifically, what do we get for

    \begin{equation}\label{eqn:qmLecture16:80}
    \lr{\hat{\BL}_1 + \hat{\BL}_2}^2,
    \end{equation}

    and for
    \begin{equation}\label{eqn:qmLecture16:100}
    \lr{\hat{L}_{1z} + \hat{L}_{2z}}.
    \end{equation}

    For the latter, we get

    \begin{equation}\label{eqn:qmLecture16:120}
    \lr{\hat{L}_{1z} + \hat{L}_{2z}}\ket{ l_1, m_1 ; l_2, m_2 }
    =
    \lr{ \Hbar m_1 + \Hbar m_2 } \ket{ l_1, m_1 ; l_2, m_2 }
    \end{equation}

    Given
    \begin{equation}\label{eqn:qmLecture16:140}
    \hat{L}_{1z} + \hat{L}_{2z} = \hat{L}_z^{\textrm{tot}},
    \end{equation}

    we find
    \begin{equation}\label{eqn:qmLecture16:160}
    \begin{aligned}
    \antisymmetric{\hat{L}_z^{\textrm{tot}}}{\hat{\BL}_1^2} &= 0 \\
    \antisymmetric{\hat{L}_z^{\textrm{tot}}}{\hat{\BL}_2^2} &= 0 \\
    \antisymmetric{\hat{L}_z^{\textrm{tot}}}{\hat{\BL}_{1z}} &= 0 \\
    \antisymmetric{\hat{L}_z^{\textrm{tot}}}{\hat{\BL}_{1z}} &= 0.
    \end{aligned}
    \end{equation}

    We also find

    \begin{equation}\label{eqn:qmLecture16:180}
    \begin{aligned}
    \antisymmetric{(\hat{\BL}_1 + \hat{\BL}_2)^2}{\BL_1^2}
    &=
    \antisymmetric{\hat{\BL}_1^2 + \hat{\BL}_2^2 + 2 \hat{\BL}_1 \cdot
    \hat{\BL}_2}{\BL_1^2} \\
    &=
    0,
    \end{aligned}
    \end{equation}

    but for
    \begin{equation}\label{eqn:qmLecture16:200}
    \begin{aligned}
    \antisymmetric{(\hat{\BL}_1 + \hat{\BL}_2)^2}{\hat{L}_{1z}}
    &=
    \antisymmetric{\hat{\BL}_1^2 + \hat{\BL}_2^2 + 2 \hat{\BL}_1 \cdot
    \hat{\BL}_2}{\hat{L}_{1z}} \\
    &=
    2 \antisymmetric{\hat{\BL}_1 \cdot \hat{\BL}_2}{\hat{L}_{1z}} \\
    &\ne 0.
    \end{aligned}
    \end{equation}

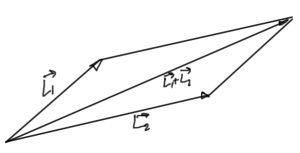
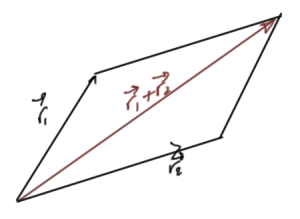
Classically if we have measured \( \hat{\BL}_{1} \) and \( \hat{\BL}_{2} \) then we know the total angular momentum as sketched in fig. 1.

fig. 1. Classical addition of angular momenta.

fig. 1. Classical addition of angular momenta.

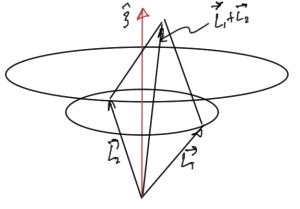
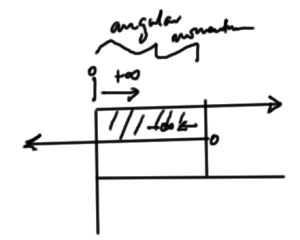
In QM where we don’t know all the components of the angular momenum simultaneously, things get fuzzier. For example, if the \( \hat{L}_{1z} \) and \( \hat{L}_{2z} \) components have been measured, we have the angular momentum defined within a conical region as sketched in fig. 2.

fig. 2. Addition of angular momenta given measured L_z

fig. 2. Addition of angular momenta given measured L_z

Suppose we know \( \hat{L}_z^{\textrm{tot}} \) precisely, but have impricise information about \( \lr{\hat{\BL}^{\textrm{tot}}}^2 \). Can we determine bounds for this? Let \( \ket{\psi} = \ket{ l_1, m_2 ; l_2, m_2 } \), so

\begin{equation}\label{eqn:qmLecture16:220}
\begin{aligned}
\bra{\psi} \lr{ \hat{\BL}_1 + \hat{\BL}_2 }^2 \ket{\psi}
&=
\bra{\psi} \hat{\BL}_1^2 \ket{\psi}
+ \bra{\psi} \hat{\BL}_2^2 \ket{\psi}
+ 2 \bra{\psi} \hat{\BL}_1 \cdot \hat{\BL}_2 \ket{\psi} \\
&=
l_1 \lr{ l_1 + 1} \Hbar^2
+ l_2 \lr{ l_2 + 1} \Hbar^2
+ 2
\bra{\psi} \hat{\BL}_1 \cdot \hat{\BL}_2 \ket{\psi}.
\end{aligned}
\end{equation}

Using the Cauchy-Schwartz inequality

\begin{equation}\label{eqn:qmLecture16:240}
\Abs{\braket{\phi}{\psi}}^2 \le
\Abs{\braket{\phi}{\phi}}
\Abs{\braket{\psi}{\psi}},
\end{equation}

which is the equivalent of the classical relationship
\begin{equation}\label{eqn:qmLecture16:260}
\lr{ \BA \cdot \BB }^2 \le \BA^2 \BB^2.
\end{equation}

Applying this to the last term, we have

\begin{equation}\label{eqn:qmLecture16:280}
\begin{aligned}
\lr{ \bra{\psi} \hat{\BL}_1 \cdot \hat{\BL}_2 \ket{\psi} }^2
&\le
\bra{ \psi} \hat{\BL}_1 \cdot \hat{\BL}_1 \ket{\psi}
\bra{ \psi} \hat{\BL}_2 \cdot \hat{\BL}_2 \ket{\psi} \\
&=
\Hbar^4
l_1 \lr{ l_1 + 1 }
l_2 \lr{ l_2 + 2 }.
\end{aligned}
\end{equation}

Thus for the max we have

\begin{equation}\label{eqn:qmLecture16:300}
\bra{\psi} \lr{ \hat{\BL}_1 + \hat{\BL}_2 }^2 \ket{\psi}
\le
\Hbar^2 l_1 \lr{ l_1 + 1 }
+\Hbar^2 l_2 \lr{ l_2 + 1 }
+ 2 \Hbar^2 \sqrt{ l_1 \lr{ l_1 + 1 } l_2 \lr{ l_2 + 2 } }
\end{equation}

and for the min
\begin{equation}\label{eqn:qmLecture16:360}
\bra{\psi} \lr{ \hat{\BL}_1 + \hat{\BL}_2 }^2 \ket{\psi}
\ge
\Hbar^2 l_1 \lr{ l_1 + 1 }
+\Hbar^2 l_2 \lr{ l_2 + 1 }
– 2 \Hbar^2 \sqrt{ l_1 \lr{ l_1 + 1 } l_2 \lr{ l_2 + 2 } }.
\end{equation}

To try to pretty up these estimate, starting with the max, note that if we replace a portion of the RHS with something bigger, we are left with a strict less than relationship.

That is

\begin{equation}\label{eqn:qmLecture16:320}
\begin{aligned}
l_1 \lr{ l_1 + 1 } &< \lr{ l_1 + \inv{2} }^2 \\ l_2 \lr{ l_2 + 1 } &< \lr{ l_2 + \inv{2} }^2 \end{aligned} \end{equation} That is \begin{equation}\label{eqn:qmLecture16:340} \begin{aligned} \bra{\psi} \lr{ \hat{\BL}_1 + \hat{\BL}_2 }^2 \ket{\psi} &< \Hbar^2 \lr{ l_1 \lr{ l_1 + 1 } + l_2 \lr{ l_2 + 1 } + 2 \lr{ l_1 + \inv{2} } \lr{ l_2 + \inv{2} } } \\ &= \Hbar^2 \lr{ l_1^2 + l_2^2 + l_1 + l_2 + 2 l_1 l_2 + l_1 + l_2 + \inv{2} } \\ &= \Hbar^2 \lr{ \lr{ l_1 + l_2 + \inv{2} } \lr{ l_1 + l_2 + \frac{3}{2} } - \inv{4} } \end{aligned} \end{equation} or \begin{equation}\label{eqn:qmLecture16:380} l_{\textrm{tot}} \lr{ l_{\textrm{tot}} + 1 } < \lr{ l_1 + l_2 + \inv{2} } \lr{ l_1 + l_2 + \frac{3}{2} } , \end{equation} which, gives \begin{equation}\label{eqn:qmLecture16:400} l_{\textrm{tot}} < l_1 + l_2 + \inv{2}. \end{equation} Finally, given a quantization requirement, that is \begin{equation}\label{eqn:t:1} \boxed{ l_{\textrm{tot}} \le l_1 + l_2. } \end{equation} Similarly, for the min, we find \begin{equation}\label{eqn:qmLecture16:440} \begin{aligned} \bra{\psi} \lr{ \hat{\BL}_1 + \hat{\BL}_2 }^2 \ket{\psi} &>
\Hbar^2
\lr{
l_1 \lr{ l_1 + 1 }
+ l_2 \lr{ l_2 + 1 }
– 2 \lr{ l_1 + \inv{2} } \lr{ l_2 + \inv{2} }
} \\
&=
\Hbar^2
\lr{
l_1^2 + l_2^2 %+ \cancel{l_1 + l_2}
– 2 l_1 l_2
– \inv{2}
}
\end{aligned}
\end{equation}

This will be finished Thursday, but we should get

\begin{equation}\label{eqn:t:2}
\boxed{
\Abs{l_1 – l_2} \le l_{\textrm{tot}} \le l_1 + l_2.
}
\end{equation}

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

Two spin time evolution

November 14, 2015 phy1520 , , , ,

[Click here for a PDF of this post with nicer formatting]

Motivation

Our midterm posed a (low mark “quick question”) that I didn’t complete (or at least not properly). This shouldn’t have been a difficult question, but I spend way too much time on it, costing me time that I needed for other questions.

It turns out that there isn’t anything fancy required for this question, just perseverance and careful work.

Guts

The question asked for the time evolution of a two particle state

\begin{equation}\label{eqn:twoSpinHamiltonian:20}
\psi = \inv{\sqrt{2}} \lr{ \ket{\uparrow \downarrow} – \ket{\downarrow \uparrow} }
\end{equation}

under the action of the Hamiltonian

\begin{equation}\label{eqn:twoSpinHamiltonian:40}
H = – B S_{z,1} + 2 B S_{x,2} = \frac{\Hbar B}{2}\lr{ -\sigma_{z,1} + 2 \sigma_{x,2} } .
\end{equation}

We have to know the action of the Hamiltonian on all the states

\begin{equation}\label{eqn:twoSpinHamiltonian:60}
\begin{aligned}
H \ket{\uparrow \uparrow} &= \frac{B \Hbar}{2} \lr{ -\ket{\uparrow \uparrow} + 2 \ket{\uparrow \downarrow} } \\
H \ket{\uparrow \downarrow} &= \frac{B \Hbar}{2} \lr{ -\ket{\uparrow \downarrow} + 2 \ket{\uparrow \uparrow} } \\
H \ket{\downarrow \uparrow} &= \frac{B \Hbar}{2} \lr{ \ket{\downarrow \uparrow} + 2 \ket{\downarrow \downarrow} } \\
H \ket{\downarrow \downarrow} &= \frac{B \Hbar}{2} \lr{ \ket{\downarrow \downarrow} + 2 \ket{\downarrow \uparrow} } \\
\end{aligned}
\end{equation}

With respect to the basis \( \setlr{ \ket{\uparrow \uparrow}, \ket{\uparrow \downarrow}, \ket{\downarrow \uparrow}, \ket{\downarrow \downarrow} } \), the matrix of the Hamiltonian is

\begin{equation}\label{eqn:twoSpinHamiltonian:80}
H =
\frac{ \Hbar B }{2}
\begin{bmatrix}
-1 & 2 & 0 & 0 \\
2 & -1 & 0 & 0 \\
0 & 0 & 1 & 2 \\
0 & 0 & 2 & 1 \\
\end{bmatrix}
\end{equation}

Utilizing the block diagonal form (and ignoring the \( \Hbar B/2 \) factor for now), the characteristic equation is

\begin{equation}\label{eqn:twoSpinHamiltonian:100}
0
=
\begin{vmatrix}
-1 -\lambda & 2 \\
2 & -1 – \lambda
\end{vmatrix}
\begin{vmatrix}
1 -\lambda & 2 \\
2 & 1 – \lambda
\end{vmatrix}
=
\lr{(1 + \lambda)^2 – 4}
\lr{(1 – \lambda)^2 – 4}.
\end{equation}

This has solutions

\begin{equation}\label{eqn:twoSpinHamiltonian:120}
1 \pm \lambda = \pm 2,
\end{equation}

or, with the \( \Hbar B/2 \) factors put back in

\begin{equation}\label{eqn:twoSpinHamiltonian:140}
\lambda = \pm \Hbar B/2 , \pm 3 \Hbar B/2.
\end{equation}

I was thinking that we needed to compute the time evolution operator

\begin{equation}\label{eqn:twoSpinHamiltonian:160}
U = e^{-i H t/\Hbar},
\end{equation}

but we actually only need the eigenvectors, and the inverse relations. We can find the eigenvectors by inspection in each case from

\begin{equation}\label{eqn:twoSpinHamiltonian:180}
\begin{aligned}
H – (1) \frac{ \Hbar B }{2}
&=
\frac{ \Hbar B }{2}
\begin{bmatrix}
-2 & 2 & 0 & 0 \\
2 & -2 & 0 & 0 \\
0 & 0 & 0 & 2 \\
0 & 0 & 2 & 0 \\
\end{bmatrix} \\
H – (-1) \frac{ \Hbar B }{2}
&=
\frac{ \Hbar B }{2}
\begin{bmatrix}
0 & 2 & 0 & 0 \\
2 & 0 & 0 & 0 \\
0 & 0 & 2 & 2 \\
0 & 0 & 2 & 2 \\
\end{bmatrix} \\
H – (3) \frac{ \Hbar B }{2}
&=
\frac{ \Hbar B }{2}
\begin{bmatrix}
-4 & 2 & 0 & 0 \\
2 & -4 & 0 & 0 \\
0 & 0 &-2 & 2 \\
0 & 0 & 2 &-2 \\
\end{bmatrix} \\
H – (-3) \frac{ \Hbar B }{2}
&=
\frac{ \Hbar B }{2}
\begin{bmatrix}
2 & 2 & 0 & 0 \\
2 & 2 & 0 & 0 \\
0 & 0 & 4 & 2 \\
0 & 0 & 2 & 1 \\
\end{bmatrix}.
\end{aligned}
\end{equation}

The eigenkets are

\begin{equation}\label{eqn:twoSpinHamiltonian:280}
\begin{aligned}
\ket{1} &=
\inv{\sqrt{2}}
\begin{bmatrix}
1 \\
1 \\
0 \\
0 \\
\end{bmatrix} \\
\ket{-1} &=
\inv{\sqrt{2}}
\begin{bmatrix}
0 \\
0 \\
1 \\
-1 \\
\end{bmatrix} \\
\ket{3} &=
\inv{\sqrt{2}}
\begin{bmatrix}
0 \\
0 \\
1 \\
1 \\
\end{bmatrix} \\
\ket{-3} &=
\inv{\sqrt{2}}
\begin{bmatrix}
1 \\
-1 \\
0 \\
0 \\
\end{bmatrix},
\end{aligned}
\end{equation}

or

\begin{equation}\label{eqn:twoSpinHamiltonian:300}
\begin{aligned}
\sqrt{2} \ket{1} &= \ket{\uparrow \uparrow} + \ket{\uparrow \downarrow} \\
\sqrt{2} \ket{-1} &= \ket{\downarrow \uparrow} – \ket{\downarrow \downarrow} \\
\sqrt{2} \ket{3} &= \ket{\downarrow \uparrow} + \ket{\downarrow \downarrow} \\
\sqrt{2} \ket{-3} &= \ket{\uparrow \uparrow} – \ket{\uparrow \downarrow}.
\end{aligned}
\end{equation}

We can invert these

\begin{equation}\label{eqn:twoSpinHamiltonian:220}
\begin{aligned}
\ket{\uparrow \uparrow} &= \inv{\sqrt{2}} \lr{ \ket{1} + \ket{-3} } \\
\ket{\uparrow \downarrow} &= \inv{\sqrt{2}} \lr{ \ket{1} – \ket{-3} } \\
\ket{\downarrow \uparrow} &= \inv{\sqrt{2}} \lr{ \ket{3} + \ket{-1} } \\
\ket{\downarrow \downarrow} &= \inv{\sqrt{2}} \lr{ \ket{3} – \ket{-1} } \\
\end{aligned}
\end{equation}

The original state of interest can now be expressed in terms of the eigenkets

\begin{equation}\label{eqn:twoSpinHamiltonian:240}
\psi
=
\inv{2} \lr{
\ket{1} – \ket{-3} –
\ket{3} – \ket{-1}
}
\end{equation}

The time evolution of this ket is

\begin{equation}\label{eqn:twoSpinHamiltonian:260}
\begin{aligned}
\psi(t)
&=
\inv{2}
\lr{
e^{-i B t/2} \ket{1}
– e^{3 i B t/2} \ket{-3}
– e^{-3 i B t/2} \ket{3}
– e^{i B t/2} \ket{-1}
} \\
&=
\inv{2 \sqrt{2}}
\Biglr{
e^{-i B t/2} \lr{ \ket{\uparrow \uparrow} + \ket{\uparrow \downarrow} }
– e^{3 i B t/2} \lr{ \ket{\uparrow \uparrow} – \ket{\uparrow \downarrow} }
– e^{-3 i B t/2} \lr{ \ket{\downarrow \uparrow} + \ket{\downarrow \downarrow} }
– e^{i B t/2} \lr{ \ket{\downarrow \uparrow} – \ket{\downarrow \downarrow} }
} \\
&=
\inv{2 \sqrt{2}}
\Biglr{
\lr{ e^{-i B t/2} – e^{3 i B t/2} } \ket{\uparrow \uparrow}
+ \lr{ e^{-i B t/2} + e^{3 i B t/2} } \ket{\uparrow \downarrow}
– \lr{ e^{-3 i B t/2} + e^{i B t/2} } \ket{\downarrow \uparrow}
+ \lr{ e^{i B t/2} – e^{-3 i B t/2} } \ket{\downarrow \downarrow}
} \\
&=
\inv{2 \sqrt{2}}
\Biglr{
e^{i B t/2} \lr{ e^{-2 i B t/2} – e^{2 i B t/2} } \ket{\uparrow \uparrow}
+ e^{i B t/2} \lr{ e^{-2 i B t/2} + e^{2 i B t/2} } \ket{\uparrow \downarrow}
– e^{- i B t/2} \lr{ e^{-2 i B t/2} + e^{2 i B t/2} } \ket{\downarrow \uparrow}
+ e^{- i B t/2} \lr{ e^{2 i B t/2} – e^{-2 i B t/2} } \ket{\downarrow \downarrow}
} \\
&=
\inv{\sqrt{2}}
\lr{
i \sin( B t )
\lr{
e^{- i B t/2} \ket{\downarrow \downarrow} – e^{i B t/2} \ket{\uparrow \uparrow}
}
+ \cos( B t ) \lr{
e^{i B t/2} \ket{\uparrow \downarrow}
– e^{- i B t/2} \ket{\downarrow \uparrow}
}
}
\end{aligned}
\end{equation}

Note that this returns to the original state when \( t = \frac{2 \pi n}{B}, n \in \mathbb{Z} \). I think I’ve got it right this time (although I got a slightly different answer on paper before typing it up.)

This doesn’t exactly seem like a quick answer question, at least to me. Is there some easier way to do it?

PHY1520H Graduate Quantum Mechanics. Lecture 15: angular momentum rotation representation, and angular momentum addition. Taught by Prof. Arun Paramekanti

November 12, 2015 phy1520 , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course PHY1520, Graduate Quantum Mechanics, taught by Prof. Paramekanti, covering chap 3. content from [1].

Angular momentum (wrap up.)

We found

\begin{equation}\label{eqn:qmLecture15:20}
\begin{aligned}
\hat{\BL^2} \ket{j, m} &= j(j+1) \Hbar^2 \ket{j,m} \\
\hat{L}_z \ket{j, m} &= \Hbar m \ket{j,m} \\
\hat{L}_{\pm} \ket{j, m } &= \Hbar \sqrt{(j \mp m)(j \pm m + 1)} \ket{j, m \pm 1 }
\end{aligned}
\end{equation}

or Schwinger

\begin{equation}\label{eqn:qmLecture15:40}
\begin{aligned}
\hat{L}_z &= \inv{2} \lr{ \hat{n}_1 – \hat{n}_2 } \Hbar \\
\hat{L}_{+} &= a_1^\dagger a_2 \Hbar \\
\hat{L}_{-} &= a_1 a_2^\dagger \Hbar \\
j &= \inv{2} \lr{ \hat{n}_1 + \hat{n}_2 },
\end{aligned}
\end{equation}

where each of the \( a_1, a_2 \) operators obey

\begin{equation}\label{eqn:qmLecture15:60}
\begin{aligned}
\antisymmetric{a_1}{a_1^\dagger} &= 1 \\
\antisymmetric{a_2}{a_2^\dagger} &= 1
\end{aligned}
\end{equation}

and any pair of different index \( a \) operators commute, as in

\begin{equation}\label{eqn:qmLecture15:80}
\antisymmetric{a_1}{a_2^\dagger} = 0.
\end{equation}

Representations

It’s possible to compute matrix representations of the rotation operators

\begin{equation}\label{eqn:qmLecture15:100}
\hat{R}_\ncap(\phi) = e^{i \hat{\BL} \cdot \ncap \phi/\Hbar}.
\end{equation}

With respect to a ket it’s possible to find

\begin{equation}\label{eqn:qmLecture15:120}
e^{i \hat{\BL} \cdot \ncap \phi/\Hbar} \ket{j, m}
=
\sum_{m’} d^j_{m m’}(\ncap, \phi) \ket{ j, m’ }.
\end{equation}

This has a block diagonal form that’s sketched in fig. 1.

fig. 1. Block diagonal form for angular momentum matrix representation.

fig. 1. Block diagonal form for angular momentum matrix representation.

We can view \( d^j_{m m’}(\ncap, \phi) \) as a matrix, representing the rotation. The problem of determining these matrices can be reduced to that of determining the matrix for \( \hat{\BL} \), because once we have that we can exponentiate that.

Example: spin 1/2

From the eigenvalue relationships, with basis states

\begin{equation}\label{eqn:qmLecture15:160}
\begin{aligned}
\ket{\uparrow} &=
\begin{bmatrix}
1 \\
0
\end{bmatrix} \\
\ket{\downarrow} &=
\begin{bmatrix}
0 \\
1 \\
\end{bmatrix}
\end{aligned}
\end{equation}

we find

\begin{equation}\label{eqn:qmLecture15:180}
\begin{aligned}
\hat{L}_z &= \frac{\Hbar}{2} \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} \\
\hat{L}_{+} &= \frac{\Hbar}{2}
\begin{bmatrix}
0 & 1 \\
0 & 0
\end{bmatrix} \\
\hat{L}_{-} &= \frac{\Hbar}{2}
\begin{bmatrix}
0 & 0 \\
1 & 0
\end{bmatrix}.
\end{aligned}
\end{equation}

Rearranging we find the Pauli matrices

\begin{equation}\label{eqn:qmLecture15:200}
\hat{L}_k = \inv{2} \Hbar \sigma_i.
\end{equation}

Noting that \( \lr{ \Bsigma \cdot \ncap }^2 = 1 \), and \( \lr{\Bsigma \cdot \ncap }^3 = \Bsigma \cdot \ncap \), the rotation matrix is

\begin{equation}\label{eqn:qmLecture15:220}
e^{ i \Bsigma \cdot \ncap \phi/2 } \ket{\inv{2}, m} = \lr{ \cos( \phi/2 ) + i \Bsigma \cdot \ncap \sin(\phi/2) } \ket{\inv{2}, m}.
\end{equation}

The steps are

  1. Enumerate the states.
    \begin{equation}\label{eqn:qmLecture15:140}
    j_1 = \inv{2} \leftrightarrow\, \mbox{2 states (dimension of irrep = 2)}
    \end{equation}

  2. Construct the \( \hat{\BL} \) matrices.
  3. Construct \( d_{m m’}^j(\ncap, \phi) \).

Angular momentum operator in space representation

For \( L = 1 \) it turns out that the rotation matrices turn out to be the 3D rotation matrices. In the space representation

\begin{equation}\label{eqn:qmLecture15:240}
\BL = \Br \cross \Bp,
\end{equation}

the coordinates of the operator are

\begin{equation}\label{eqn:qmLecture15:260}
\hat{L}_k = i \epsilon_{k m n} r_m \lr{ -i \Hbar \PD{r_n}{} }
\end{equation}

We see that scaling \( \Br \rightarrow \alpha \Br \) does not change this operator, allowing for an angular representation \( \hat{L}_k(\theta, \phi) \) that have the form

\begin{equation}\label{eqn:qmLecture15:280}
\begin{aligned}
\hat{L}_z &= -i \Hbar \PD{\phi}{} \\
\hat{L}_{\pm} &= \Hbar \lr{ \pm \PD{\theta}{} + i \cot \theta \PD{\phi}{} }.
\end{aligned}
\end{equation}

Here \( \theta \) and \( \phi \) are the polar and azimuthal angles respectively as illustrated in fig. 2.

fig. 2. Spherical coordinate convention.

fig. 2. Spherical coordinate convention.

The equivalent wave function representation of the problem is

\begin{equation}\label{eqn:qmLecture15:300}
\begin{aligned}
\hat{\BL} Y_{lm}(\theta, \phi) &= \Hbar^2 l (l + 1) Y_{lm}(\theta, \phi) \\
\hat{L}_z Y_{lm}(\theta, \phi) &= \Hbar m Y_{lm}(\theta, \phi) \\
\end{aligned}
\end{equation}

One can find these functions

\begin{equation}\label{eqn:qmLecture15:320}
Y_{lm}(\theta, \phi) = P_{l, m}(\cos \theta) e^{i m \phi},
\end{equation}

where \( P_{l, m}(\cos \theta) \) are called the associated Legendre polynomials. This can be applied whenever we have

\begin{equation}\label{eqn:qmLecture15:340}
\antisymmetric{H}{\hat{L}_k} = 0.
\end{equation}

where all the eigenfunctions will have the form

\begin{equation}\label{eqn:qmLecture15:360}
\Psi(r, \theta, \phi) = R(r) Y_{lm}(\theta, \phi).
\end{equation}

Addition of angular momentum

Since \( \hat{\BL} \) is a vector we expect to be able to add angular momentum in some way similar to the addition of classical vectors as illustrated in fig. 3.

fig. 3. Classical vector addition.

fig. 3. Classical vector addition.

When we have a potential that depends only on the difference in position \( V(\Br_1 – \Br_2) \) then we know from classical problems it is effective to work in center of mass coordinates

\begin{equation}\label{eqn:qmLecture15:380}
\begin{aligned}
\hat{\BR}_{\textrm{cm}} &= \frac{\hat{\Br}_1 + \hat{\Br}_2}{2} \\
\hat{\BP}_{\textrm{cm}} &= \hat{\Bp}_1 + \hat{\Bp}_2
\end{aligned}
\end{equation}

where

\begin{equation}\label{eqn:qmLecture15:400}
\antisymmetric{\hat{R}_i}{\hat{P}_j} = i \Hbar \delta_{ij}.
\end{equation}

Given

\begin{equation}\label{eqn:qmLecture15:420}
\hat{\BL}_1 + \hat{\BL}_2 = \hat{\BL}_{\textrm{tot}},
\end{equation}

do we have
\begin{equation}\label{eqn:qmLecture15:440}
\antisymmetric{
\hat{L}_{\textrm{tot}, i}
}{
\hat{L}_{\textrm{tot}, j}
}
= i \Hbar \epsilon_{i j k} \hat{L}_{\textrm{tot}, k} ?
\end{equation}

That is

\begin{equation}\label{eqn:qmLecture15:460}
\antisymmetric{\hat{L}_{1,i} + \hat{L}_{1,j}}{\hat{L}_{2,i} + \hat{L}_{2,j}} = i \Hbar \epsilon_{i j k} \lr{ \hat{L}_{1,k} + \hat{L}_{1,k} }
\end{equation}

FIXME: Right at the end of the lecture, there was a mention of something about whether or not \( \hat{\BL}_1^2 \) and \( \hat{L}_{1,z} \) were sharply defined, but I missed it. Ask about this if not covered in the next lecture.

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

PHY1520H Graduate Quantum Mechanics. Lecture 14: Angular momentum (cont.). Taught by Prof. Arun Paramekanti

November 11, 2015 phy1520 , , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course PHY1520, Graduate Quantum Mechanics, taught by Prof. Paramekanti, covering [1] chap. 3 content.

Review: Angular momentum

Given eigenket \( \ket{a, b} \), where

\begin{equation}\label{eqn:qmLecture14:20}
\begin{aligned}
\hat{\BL}^2 \ket{a, b} &= \Hbar^2 a \ket{a,b} \\
\hat{L}_z \ket{a, b} &= \Hbar b \ket{a,b}
\end{aligned}
\end{equation}

We were looking for

\begin{equation}\label{eqn:qmLecture14:40}
\hat{L}_{x,y} \ket{a,b} = \sum_{b’} \mathcal{A}^{x,y}_{a; b, b’} \ket{a,b’},
\end{equation}

by applying

\begin{equation}\label{eqn:qmLecture14:60}
\hat{L}_{\pm} = \hat{L}_x \pm i \hat{L}_y.
\end{equation}

We found

\begin{equation}\label{eqn:qmLecture14:80}
\hat{L}_{\pm} \propto \ket{a, b \pm 1}.
\end{equation}

Let

\begin{equation}\label{eqn:qmLecture14:100}
\ket{\phi_\pm} = \hat{L}_{\pm} \ket{a, b}.
\end{equation}

We want

\begin{equation}\label{eqn:qmLecture14:120}
\braket{\phi_\pm}{\phi_\pm} \ge 0,
\end{equation}

or
\begin{equation}\label{eqn:qmLecture14:140}
\begin{aligned}
\bra{a,b} \hat{L}_{+} \hat{L}_{-} \ket{a, b} &\ge 0 \\
\bra{a,b} \hat{L}_{-} \hat{L}_{+} \ket{a, b} &\ge 0
\end{aligned}
\end{equation}

We found

\begin{equation}\label{eqn:qmLecture14:160}
\begin{aligned}
\hat{L}_{+} \hat{L}_{-} =
\lr{ \hat{L}_x + i \hat{L}_y } \lr{ \hat{L}_x – i \hat{L}_y }
&= \lr{ \hat{\BL}^2 – \hat{L}_z^2 } -i \antisymmetric{\hat{L}_x}{\hat{L}_y} \\
&= \lr{ \hat{\BL}^2 – \hat{L}_z^2 } -i \lr{ i \Hbar \hat{L}_z } \\
&= \lr{ \hat{\BL}^2 – \hat{L}_z^2 } + \Hbar \hat{L}_z,
\end{aligned}
\end{equation}

so

\begin{equation}\label{eqn:qmLecture14:180}
\bra{a,b} \hat{L}_{+} \hat{L}_{-} \ket{a, b}
=
\expectation{ \hat{\BL}^2 – \hat{L}_z^2 + \Hbar \hat{L}_z }.
\end{equation}

Similarly
\begin{equation}\label{eqn:qmLecture14:200}
\bra{a,b} \hat{L}_{-} \hat{L}_{+} \ket{a, b}
=
\expectation{ \hat{\BL}^2 – \hat{L}_z^2 – \Hbar \hat{L}_z }.
\end{equation}

Constraints

\begin{equation}\label{eqn:qmLecture14:220}
\begin{aligned}
a – b^2 + b &\ge 0 \\
a – b^2 – b &\ge 0
\end{aligned}
\end{equation}

If these are satisfied at the equality extreme we have

\begin{equation}\label{eqn:qmLecture14:240}
\begin{aligned}
b_{\textrm{max}} \lr{ b_{\textrm{max}} + 1 } &= a \\
b_{\textrm{min}} \lr{ b_{\textrm{min}} – 1 } &= a.
\end{aligned}
\end{equation}

Rearranging this to solve, we can rewrite the equality as

\begin{equation}\label{eqn:qmLecture14:680}
\lr{ b_{\textrm{max}} + \inv{2} }^2 – \inv{4} = \lr{ b_{\textrm{min}} – \inv{2} }^2 – \inv{4},
\end{equation}

which has solutions at

\begin{equation}\label{eqn:qmLecture14:700}
b_{\textrm{max}} + \inv{2} = \pm \lr{ b_{\textrm{min}} – \inv{2} }.
\end{equation}

One of the solutions is

\begin{equation}\label{eqn:qmLecture14:260}
-b_{\textrm{min}} = b_{\textrm{max}}.
\end{equation}

The other solution is \( b_{\textrm{max}} = b_{\textrm{min}} – 1 \), which we discard.

The final constraint is therefore

\begin{equation}\label{eqn:qmLecture14:280}
\boxed{
– b_{\textrm{max}} \le b \le b_{\textrm{max}},
}
\end{equation}

and

\begin{equation}\label{eqn:qmLecture14:320}
\begin{aligned}
\hat{L}_{+} \ket{a, b_{\textrm{max}}} &= 0 \\
\hat{L}_{-} \ket{a, b_{\textrm{min}}} &= 0
\end{aligned}
\end{equation}

If we had the sequence, which must terminate at \( b_{\textrm{min}} \) or else it will go on forever

\begin{equation}\label{eqn:qmLecture14:340}
\ket{a, b_{\textrm{max}}}
\overset{\hat{L}_{-}}{\rightarrow}
\ket{a, b_{\textrm{max}} – 1}
\overset{\hat{L}_{-}}{\rightarrow}
\ket{a, b_{\textrm{max}} – 2}
\cdots
\overset{\hat{L}_{-}}{\rightarrow}
\ket{a, b_{\textrm{min}}},
\end{equation}

then we know that \( b_{\textrm{max}} – b_{\textrm{min}} \in \mathbb{Z} \), or

\begin{equation}\label{eqn:qmLecture14:360}
b_{\textrm{max}} – n = b_{\textrm{min}} = -b_{\textrm{max}}
\end{equation}

or

\begin{equation}\label{eqn:qmLecture14:380}
b_{\textrm{max}} = \frac{n}{2},
\end{equation}

this is either an integer or a \( 1/2 \) odd integer, depending on whether \( n \) is even or odd. These are called “orbital” or “spin” respectively.

The convention is to write

\begin{equation}\label{eqn:qmLecture14:400}
\begin{aligned}
b_{\textrm{max}} &= j \\
a &= j(j + 1).
\end{aligned}
\end{equation}

so for \( m \in -j, -j + 1, \cdots, +j \)

\begin{equation}\label{eqn:qmLecture14:420}
\boxed{
\begin{aligned}
\hat{\BL}^2 \ket{j, m} &= \Hbar^2 j (j + 1) \ket{j, m} \\
L_z \ket{j, m} &= \Hbar m \ket{j, m}.
\end{aligned}
}
\end{equation}

Schwinger’s Harmonic oscillator representation of angular momentum operators.

In [2] a powerful method for describing angular momentum with harmonic oscillators was introduced, which will be outlined here. The question is whether we can construct a set of harmonic oscillators that allows a mapping from

\begin{equation}\label{eqn:qmLecture14:460}
\hat{L}_{+} \leftrightarrow a^{+}?
\end{equation}

Picture two harmonic oscillators, one with states counted from one zero towards \( \infty \) and another with states counted from a different zero towards \( -\infty \), as pictured in fig. 1.

fig. 1. Overlapping SHO domains

fig. 1. Overlapping SHO domains

Is it possible that such an overlapping set of harmonic oscillators can provide the properties of the angular momentum operators? Let’s relabel the counting so that we have two sets of positive counted SHO systems, each counted in a positive direction as sketched in fig. 2.

fig. 2. Relabeling the counting for overlapping SHO systems

fig. 2. Relabeling the counting for overlapping SHO systems

It turns out that given a constraint there the number of ways to distribute particles between a pair of SHO systems, the process that can be viewed as reproducing the angular momentum action is a transfer of particles from one harmonic oscillator to the other. For \( \hat{L}_z = +j \)

\begin{equation}\label{eqn:qmLecture14:480}
\begin{aligned}
n_1 &= n_{\textrm{max}} \\
n_2 &= 0,
\end{aligned}
\end{equation}

and for \( \hat{L}_z = -j \)

\begin{equation}\label{eqn:qmLecture14:500}
\begin{aligned}
n_1 &= 0 \\
n_2 &= n_{\textrm{max}}.
\end{aligned}
\end{equation}

We can make the identifications

\begin{equation}\label{eqn:qmLecture14:520}
\hat{L}_z = \lr{ n_1 – n_2 } \frac{\Hbar}{2},
\end{equation}

and
\begin{equation}\label{eqn:qmLecture14:540}
j = \inv{2} n_{\textrm{max}},
\end{equation}

or

\begin{equation}\label{eqn:qmLecture14:560}
n_1 + n_2 = \text{fixed} = n_{\textrm{max}}
\end{equation}

Changes that keep \( n_1 + n_2 \) fixed are those that change \( n_1 \), \( n_2 \) by \( +1 \) or \( -1 \) respectively, as sketched in fig. 3.

fig. 3. Number conservation constraint.

fig. 3. Number conservation constraint.

Can we make an identification that takes

\begin{equation}\label{eqn:qmLecture14:580}
\ket{n_1, n_2} \overset{\hat{L}_{-}}{\rightarrow} \ket{n_1 – 1, n_2 + 1}?
\end{equation}

What operator in the SHO problem has this effect? Let’s try

\boxedEquation{eqn:qmLecture14:620}{
\begin{aligned}
\hat{L}_{-} &= \Hbar a_2^\dagger a_1 \\
\hat{L}_{+} &= \Hbar a_1^\dagger a_2 \\
\hat{L}_z &= \frac{\Hbar}{2} \lr{ n_1 – n_2 }
\end{aligned}
}

Is this correct? Do we need to make any scalar adjustments? We want

\begin{equation}\label{eqn:qmLecture14:640}
\antisymmetric{\hat{L}_z}{\hat{L}_{\pm}} = \pm \Hbar \hat{L}_{\pm}.
\end{equation}

First check this with the \( \hat{L}_{+} \) commutator

\begin{equation}\label{eqn:qmLecture14:660}
\begin{aligned}
\antisymmetric{\hat{L}_z}{\hat{L}_{+}}
&=
\inv{2} \Hbar^2 \antisymmetric{ n_1 – n_2}{a_1^\dagger a_2 } \\
&=
\inv{2} \Hbar^2 \antisymmetric{ a_1^\dagger a_1 – a_2^\dagger a_2 }{a_1^\dagger a_2 } \\
&=
\inv{2} \Hbar^2
\lr{
\antisymmetric{ a_1^\dagger a_1 }{a_1^\dagger a_2 }
-\antisymmetric{ a_2^\dagger a_2 }{a_1^\dagger a_2 }
} \\
&=
\inv{2} \Hbar^2
\lr{
a_2 \antisymmetric{ a_1^\dagger a_1 }{a_1^\dagger }
-a_1^\dagger \antisymmetric{ a_2^\dagger a_2 }{a_2 }
}.
\end{aligned}
\end{equation}

But

\begin{equation}\label{eqn:qmLecture14:720}
\begin{aligned}
\antisymmetric{ a^\dagger a }{a^\dagger }
&=
a^\dagger a
a^\dagger
–
a^\dagger
a^\dagger a \\
&=
a^\dagger \lr{ 1 +
a^\dagger a}
–
a^\dagger
a^\dagger a \\
&=
a^\dagger,
\end{aligned}
\end{equation}

and
\begin{equation}\label{eqn:qmLecture14:740}
\begin{aligned}
\antisymmetric{ a^\dagger a }{a}
&=
a^\dagger a a
-a a^\dagger a \\
&=
a^\dagger a a
-\lr{ 1 + a^\dagger a } a \\
&=
-a,
\end{aligned}
\end{equation}

so
\begin{equation}\label{eqn:qmLecture14:760}
\antisymmetric{\hat{L}_z}{\hat{L}_{+}} = \Hbar^2 a_2 a_1^\dagger = \Hbar \hat{L}_{+},
\end{equation}

as desired. Similarly

\begin{equation}\label{eqn:qmLecture14:780}
\begin{aligned}
\antisymmetric{\hat{L}_z}{\hat{L}_{-}}
&=
\inv{2} \Hbar^2 \antisymmetric{ n_1 – n_2}{a_2^\dagger a_1 } \\
&=
\inv{2} \Hbar^2 \antisymmetric{ a_1^\dagger a_1 – a_2^\dagger a_2 }{a_2^\dagger a_1 } \\
&=
\inv{2} \Hbar^2 \lr{
a_2^\dagger \antisymmetric{ a_1^\dagger a_1 }{a_1 }
– a_1 \antisymmetric{ a_2^\dagger a_2 }{a_2^\dagger }
} \\
&=
\inv{2} \Hbar^2 \lr{
a_2^\dagger (-a_1)
– a_1 a_2^\dagger
} \\
&=
– \Hbar^2 a_2^\dagger a_1 \\
&=
– \Hbar \hat{L}_{-}.
\end{aligned}
\end{equation}

With

\begin{equation}\label{eqn:qmLecture14:800}
\begin{aligned}
j &= \frac{n_1 + n_2}{2} \\
m &= \frac{n_1 – n_2}{2} \\
\end{aligned}
\end{equation}

We can make the identification

\begin{equation}\label{eqn:qmLecture14:820}
\ket{n_1, n_2} = \ket{ j+ m , j – m}.
\end{equation}

Another way

With

\begin{equation}\label{eqn:qmLecture14:840}
\hat{L}_{+} \ket{j, m} = d_{j,m}^{+} \ket{j, m+1}
\end{equation}

or

\begin{equation}\label{eqn:qmLecture14:860}
\Hbar a_1^\dagger a_2 \ket{j + m, j-m} = d_{j,m}^{+} \ket{ j + m + 1, j- m-1},
\end{equation}

we can seek this factor \( d_{j,m}^{+} \) by operating with \( \hat{L}_{+} \)

\begin{equation}\label{eqn:qmLecture14:880}
\begin{aligned}
\hat{L}_{+} \ket{j, m}
&=
\Hbar a_1^\dagger a_2 \ket{n_1, n_2} \\
&=
\Hbar a_1^\dagger a_2 \ket{j+m,j-m} \\
&=
\Hbar \sqrt{ n + 1 } \sqrt{n_2} \ket{j+m +1,j-m-1} \\
&=
\Hbar \sqrt{ \lr{ j+ m + 1}\lr{ j – m } } \ket{j+m +1,j-m-1}
\end{aligned}
\end{equation}

That gives
\begin{equation}\label{eqn:qmLecture14:900}
\begin{aligned}
d_{j,m}^{+} &= \Hbar \sqrt{\lr{ j – m } \lr{ j+ m + 1} } \\
d_{j,m}^{-} &= \Hbar \sqrt{\lr{ j + m } \lr{ j- m + 1} }.
\end{aligned}
\end{equation}

This equivalence can be used to model spin interaction in crystals as harmonic oscillators. This equivalence of lattice vibrations and spin oscillations is called “spin waves”.

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

[2] J Schwinger. Quantum theory of angular momentum. biedenharn l., van dam h., editors, 1955. URL http://www.ifi.unicamp.br/ cabrera/teaching/paper_schwinger.pdf.

Third update of aggregate notes for phy1520, Graduate Quantum Mechanics.

November 9, 2015 phy1520 , , , , , , , , , , , , , , , ,

I’ve posted a third update of my aggregate notes for PHY1520H Graduate Quantum Mechanics, taught by Prof. Arun Paramekanti. In addition to what was noted previously, this contains lecture notes up to lecture 13, my solutions for the third problem set, and some additional worked practice problems.

Most of the content was posted individually in the following locations, but those original documents will not be maintained individually any further.