[Click here for a PDF of this post with nicer formatting]
Following [1], Maxwell’s equations in media, including both electric and magnetic sources and currents are
\begin{equation}\label{eqn:boundaryConditionsInMedia:40}
\spacegrad \cross \BE = -\BM – \partial_t \BB
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:60}
\spacegrad \cross \BH = \BJ + \partial_t \BD
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:80}
\spacegrad \cdot \BD = \rho
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:100}
\spacegrad \cdot \BB = \rho_{\textrm{m}}
\end{equation}
In general, it is not possible to assemble these into a single Geometric Algebra equation unless specific assumptions about the permeabilities are made, but we can still use Geometric Algebra to examine the boundary condition question. First, these equations can be expressed in a more natural multivector form
\begin{equation}\label{eqn:boundaryConditionsInMedia:140}
\spacegrad \wedge \BE = -I \lr{ \BM + \partial_t \BB }
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:160}
\spacegrad \wedge \BH = I \lr{ \BJ + \partial_t \BD }
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:180}
\spacegrad \cdot \BD = \rho
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:200}
\spacegrad \cdot \BB = \rho_{\textrm{m}}
\end{equation}
Then duality relations can be used on the divergences to write all four equations in their curl form
\begin{equation}\label{eqn:boundaryConditionsInMedia:240}
\spacegrad \wedge \BE = -I \lr{ \BM + \partial_t \BB }
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:260}
\spacegrad \wedge \BH = I \lr{ \BJ + \partial_t \BD }
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:280}
\spacegrad \wedge (I\BD) = \rho I
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:300}
\spacegrad \wedge (I\BB) = \rho_{\textrm{m}} I.
\end{equation}
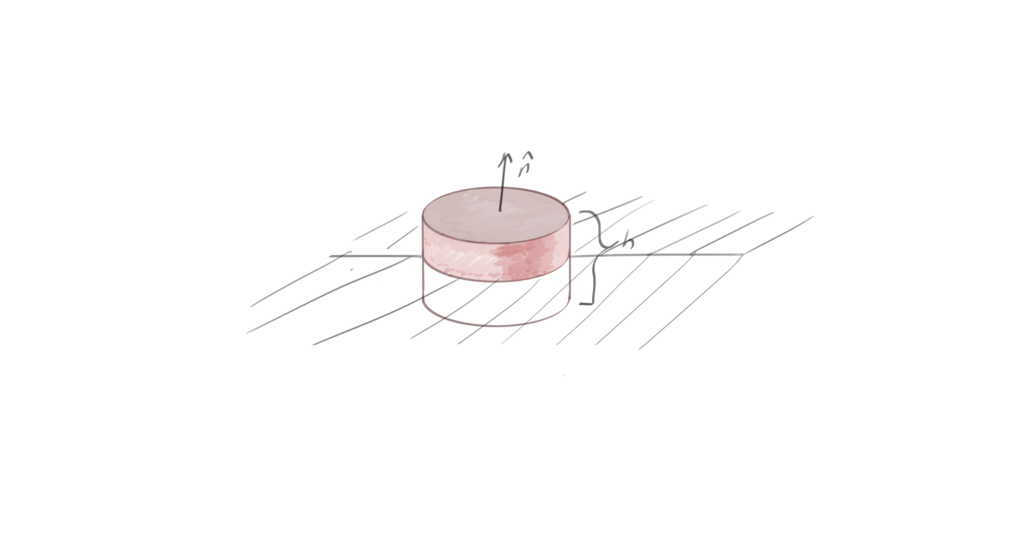
Now it is possible to employ Stokes theorem to each of these. The usual procedure is to both use the loops of fig. 2 and the pillbox of fig. 1, where in both cases the height is made infinitesimal.
With all these relations expressed in curl form as above, we can use just the pillbox configuration to evaluate the Stokes integrals.
Let the height \( h \) be measured along the normal axis, and assume that all the charges and currents are localized to the surface
\begin{equation}\label{eqn:boundaryConditionsInMedia:320}
\begin{aligned}
\BM &= \BM_{\textrm{s}} \delta( h ) \\
\BJ &= \BJ_{\textrm{s}} \delta( h ) \\
\rho &= \rho_{\textrm{s}} \delta( h ) \\
\rho_{\textrm{m}} &= \rho_{\textrm{m}\textrm{s}} \delta( h ),
\end{aligned}
\end{equation}
we can enumerate the Stokes integrals \( \int d^3 \Bx \cdot \lr{ \spacegrad \wedge \BX } = \oint_{\partial V} d^2 \Bx \cdot \BX \). The three-volume area element will be written as \( d^3 \Bx = d^2 \Bx \wedge \ncap dh \), giving
\begin{equation}\label{eqn:boundaryConditionsInMedia:360}
\oint_{\partial V} d^2 \Bx \cdot \BE = -\int (d^2 \Bx \wedge \ncap) \cdot \lr{ I \BM_{\textrm{s}} + \partial_t I \BB \Delta h}
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:380}
\oint_{\partial V} d^2 \Bx \cdot \BH = \int (d^2 \Bx \wedge \ncap) \cdot \lr{ I \BJ_{\textrm{s}} + \partial_t I \BD \Delta h}
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:400}
\oint_{\partial V} d^2 \Bx \cdot (I\BD) = \int (d^2 \Bx \wedge \ncap) \cdot \lr{ \rho_{\textrm{s}} I }
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:420}
\oint_{\partial V} d^2 \Bx \cdot (I\BB) = \int (d^2 \Bx \wedge \ncap) \cdot \lr{ \rho_{\textrm{m}\textrm{s}} I }
\end{equation}
In the limit with \( \Delta h \rightarrow 0 \), the LHS integrals are reduced to just the top and bottom surfaces, and the \( \Delta h \) contributions on the RHS are eliminated. With \( i = I \ncap \), and \( d^2 \Bx = dA\, i \) on the top surface, we are left with
\begin{equation}\label{eqn:boundaryConditionsInMedia:460}
0 = \int dA \lr{ i \cdot \Delta \BE + I \cdot \lr{ I \BM_{\textrm{s}} } }
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:480}
0 = \int dA \lr{ i \cdot \Delta \BH – I \cdot \lr{ I \BJ_{\textrm{s}} } }
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:500}
0 = \int dA \lr{ i \cdot \Delta (I\BD) + \rho_{\textrm{s}} }
\end{equation}
\begin{equation}\label{eqn:boundaryConditionsInMedia:520}
0 = \int dA \lr{ i \cdot \Delta (I\BB) + \rho_{\textrm{m}\textrm{s}} }
\end{equation}
Consider the first integral. Any component of \( \BE \) that is normal to the plane of the pillbox top (or bottom) has no contribution to the integral, so this constraint is one that effects only the tangential components \( \ncap (\ncap \wedge (\Delta \BE)) \). Writing out the vector portion of the integrand, we have
\begin{equation}\label{eqn:boundaryConditionsInMedia:540}
\begin{aligned}
i \cdot \Delta \BE + I \cdot \lr{ I \BM_{\textrm{s}} }
&=
\gpgradeone{ i \Delta \BE + I^2 \BM_{\textrm{s}} } \\
&=
\gpgradeone{ I \ncap \Delta \BE – \BM_{\textrm{s}} } \\
&=
\gpgradeone{ I \ncap \ncap (\ncap \wedge \Delta \BE) – \BM_{\textrm{s}} } \\
&=
\gpgradeone{ I (\ncap \wedge (\Delta \BE)) – \BM_{\textrm{s}} } \\
&=
\gpgradeone{ -\ncap \cross (\Delta \BE) – \BM_{\textrm{s}} }.
\end{aligned}
\end{equation}
The dot product (a scalar) in the two surface charge integrals can also be reduced
\begin{equation}\label{eqn:boundaryConditionsInMedia:560}
\begin{aligned}
i \cdot \Delta (I\BD)
&=
\gpgradezero{ i \Delta (I\BD) } \\
&=
\gpgradezero{ I \ncap \Delta (I\BD) } \\
&=
\gpgradezero{ -\ncap \Delta \BD } \\
&=
-\ncap \cdot \Delta \BD,
\end{aligned}
\end{equation}
so the integral equations are satisfied provided
\begin{equation}\label{eqn:boundaryConditionsInMedia:580}
\boxed{
\begin{aligned}
\ncap \cross (\BE_2 – \BE_1) &= – \BM_{\textrm{s}} \\
\ncap \cross (\BH_2 – \BH_1) &= \BJ_{\textrm{s}} \\
\ncap \cdot (\BD_2 – \BD_1) &= \rho_{\textrm{s}} \\
\ncap \cdot (\BB_2 – \BB_1) &= \rho_{\textrm{m}\textrm{s}}.
\end{aligned}
}
\end{equation}
It is tempting to try to assemble these into a results expressed in terms of a four-vector surface current and composite STA bivector fields like the \( F = \BE + I c \BB \) that we can use for the free space Maxwell’s equation. Dimensionally, we need something with velocity in that mix, but what velocity should be used when the speed of the field propagation in each media is potentially different?
References
[1] Constantine A Balanis. Advanced engineering electromagnetics. Wiley New York, 1989.