[Click here for a PDF of this post with nicer formatting]
The relativistic form of Maxwell’s equation in Geometric Algebra is
\begin{equation}\label{eqn:maxwellStokes:20}
\grad F = \inv{c \epsilon_0} J,
\end{equation}
where \( \grad = \gamma^\mu \partial_\mu \) is the spacetime gradient, and \( J = (c\rho, \BJ) = J^\mu \gamma_\mu \) is the four (vector) current density. The pseudoscalar for the space is denoted \( I = \gamma_0 \gamma_1 \gamma_2 \gamma_3 \), where the basis elements satisfy \( \gamma_0^2 = 1 = -\gamma_k^2 \), and a dual basis satisfies \( \gamma_\mu \cdot \gamma^\nu = \delta_\mu^\nu \). The electromagnetic field \( F \) is a composite multivector \( F = \BE + I c \BB \). This is actually a bivector because spatial vectors have a bivector representation in the space time algebra of the form \( \BE = E^k \gamma_k \gamma_0 \).
A dual representation, with \( F = I G \) is also possible
\begin{equation}\label{eqn:maxwellStokes:60}
\grad G = \frac{I}{c \epsilon_0} J.
\end{equation}
Either form of Maxwell’s equation can be split into grade one and three components. The standard (non-dual) form is
\begin{equation}\label{eqn:maxwellStokes:40}
\begin{aligned}
\grad \cdot F &= \inv{c \epsilon_0} J \\
\grad \wedge F &= 0,
\end{aligned}
\end{equation}
and the dual form is
\begin{equation}\label{eqn:maxwellStokes:41}
\begin{aligned}
\grad \cdot G &= 0 \\
\grad \wedge G &= \frac{I}{c \epsilon_0} J.
\end{aligned}
\end{equation}
In both cases a potential representation \( F = \grad \wedge A \), where \( A \) is a four vector potential can be used to kill off the non-current equation. Such a potential representation reduces Maxwell’s equation to
\begin{equation}\label{eqn:maxwellStokes:80}
\grad \cdot F = \inv{c \epsilon_0} J,
\end{equation}
or
\begin{equation}\label{eqn:maxwellStokes:100}
\grad \wedge G = \frac{I}{c \epsilon_0} J.
\end{equation}
In both cases, these reduce to
\begin{equation}\label{eqn:maxwellStokes:120}
\grad^2 A – \grad \lr{ \grad \cdot A } = \inv{c \epsilon_0} J.
\end{equation}
This can clearly be further simplified by using the Lorentz gauge, where \( \grad \cdot A = 0 \). However, the aim for now is to try applying Stokes theorem to Maxwell’s equation. The dual form \ref{eqn:maxwellStokes:100} has the curl structure required for the application of Stokes. Suppose that we evaluate this curl over the three parameter volume element \( d^3 x = i\, dx^0 dx^1 dx^2 \), where \( i = \gamma_0 \gamma_1 \gamma_2 \) is the unit pseudoscalar for the spacetime volume element.
\begin{equation}\label{eqn:maxwellStokes:101}
\begin{aligned}
\int_V d^3 x \cdot \lr{ \grad \wedge G }
&=
\int_V d^3 x \cdot \lr{ \gamma^\mu \wedge \partial_\mu G } \\
&=
\int_V \lr{ d^3 x \cdot \gamma^\mu } \cdot \partial_\mu G \\
&=
\sum_{\mu \ne 3} \int_V \lr{ d^3 x \cdot \gamma^\mu } \cdot \partial_\mu G.
\end{aligned}
\end{equation}
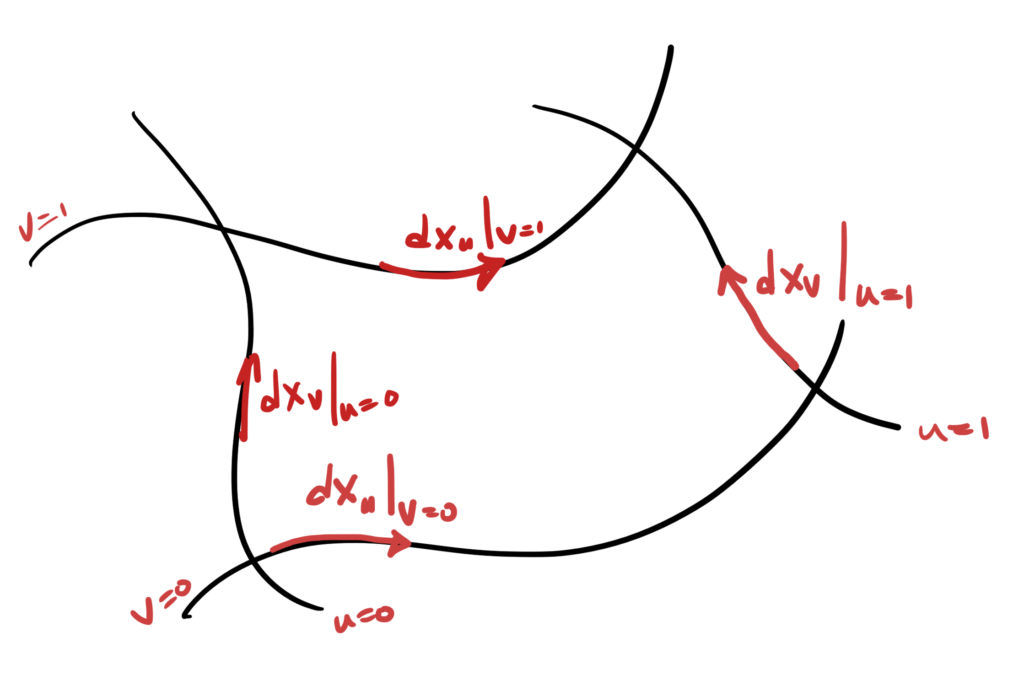
This uses the distibution identity \( A_s \cdot (a \wedge A_r) = (A_s \cdot a) \cdot A_r \) which holds for blades \( A_s, A_r \) provided \( s > r > 0 \). Observe that only the component of the gradient that lies in the tangent space of the three volume manifold contributes to the integral, allowing the gradient to be used in the Stokes integral instead of the vector derivative (see: [1]).
Defining the the surface area element
\begin{equation}\label{eqn:maxwellStokes:140}
\begin{aligned}
d^2 x
&= \sum_{\mu \ne 3} i \cdot \gamma^\mu \inv{dx^\mu} d^3 x \\
&= \gamma_1 \gamma_2 dx dy
+ c \gamma_2 \gamma_0 dt dy
+ c \gamma_0 \gamma_1 dt dx,
\end{aligned}
\end{equation}
Stokes theorem for this volume element is now completely specified
\begin{equation}\label{eqn:maxwellStokes:200}
\int_V d^3 x \cdot \lr{ \grad \wedge G }
=
\int_{\partial V} d^2 \cdot G.
\end{equation}
Application to the dual Maxwell equation gives
\begin{equation}\label{eqn:maxwellStokes:160}
\int_{\partial V} d^2 x \cdot G
= \inv{c \epsilon_0} \int_V d^3 x \cdot (I J).
\end{equation}
After some manipulation, this can be restated in the non-dual form
\begin{equation}\label{eqn:maxwellStokes:180}
\boxed{
\int_{\partial V} \inv{I} d^2 x \wedge F
= \frac{1}{c \epsilon_0 I} \int_V d^3 x \wedge J.
}
\end{equation}
It can be demonstrated that using this with each of the standard basis spacetime 3-volume elements recovers Gauss’s law and the Ampere-Maxwell equation. So, what happened to Faraday’s law and Gauss’s law for magnetism? With application of Stokes to the curl equation from \ref{eqn:maxwellStokes:40}, those equations take the form
\begin{equation}\label{eqn:maxwellStokes:240}
\boxed{
\int_{\partial V} d^2 x \cdot F = 0.
}
\end{equation}
Problem 1:
Demonstrate that the Ampere-Maxwell equation and Gauss’s law can be recovered from the trivector (curl) equation \ref{eqn:maxwellStokes:100}.
Answer
The curl equation is a trivector on each side, so dotting it with each of the four possible trivectors \( \gamma_0 \gamma_1 \gamma_2, \gamma_0 \gamma_2 \gamma_3, \gamma_0 \gamma_1 \gamma_3, \gamma_1 \gamma_2 \gamma_3 \) will give four different scalar equations. For example, dotting with \( \gamma_0 \gamma_1 \gamma_2 \), we have for the curl side
\begin{equation}\label{eqn:maxwellStokes:460}
\begin{aligned}
\lr{ \gamma_0 \gamma_1 \gamma_2 } \cdot \lr{ \gamma^\mu \wedge \partial_\mu G }
&=
\lr{ \lr{ \gamma_0 \gamma_1 \gamma_2 } \cdot \gamma^\mu } \cdot \partial_\mu G \\
&=
(\gamma_0 \gamma_1) \cdot \partial_2 G
+(\gamma_2 \gamma_0) \cdot \partial_1 G
+(\gamma_1 \gamma_2) \cdot \partial_0 G,
\end{aligned}
\end{equation}
and for the current side, we have
\begin{equation}\label{eqn:maxwellStokes:480}
\begin{aligned}
\inv{\epsilon_0 c} \lr{ \gamma_0 \gamma_1 \gamma_2 } \cdot \lr{ I J }
&=
\inv{\epsilon_0 c} \gpgradezero{ \gamma_0 \gamma_1 \gamma_2 (\gamma_0 \gamma_1 \gamma_2 \gamma_3) J } \\
&=
\inv{\epsilon_0 c} \gpgradezero{ -\gamma_3 J } \\
&=
\inv{\epsilon_0 c} \gamma^3 \cdot J \\
&=
\inv{\epsilon_0 c} J^3,
\end{aligned}
\end{equation}
so we have
\begin{equation}\label{eqn:maxwellStokes:500}
(\gamma_0 \gamma_1) \cdot \partial_2 G
+(\gamma_2 \gamma_0) \cdot \partial_1 G
+(\gamma_1 \gamma_2) \cdot \partial_0 G
=
\inv{\epsilon_0 c} J^3.
\end{equation}
Similarily, dotting with \( \gamma_{013}, \gamma_{023}, and \gamma_{123} \) respectively yields
\begin{equation}\label{eqn:maxwellStokes:620}
\begin{aligned}
\gamma_{01} \cdot \partial_3 G + \gamma_{30} \partial_1 G + \gamma_{13} \partial_0 G &= – \inv{\epsilon_0 c} J^2 \\
\gamma_{02} \cdot \partial_3 G + \gamma_{30} \partial_2 G + \gamma_{23} \partial_0 G &= \inv{\epsilon_0 c} J^1 \\
\gamma_{12} \cdot \partial_3 G + \gamma_{31} \partial_2 G + \gamma_{23} \partial_1 G &= -\inv{\epsilon_0} \rho.
\end{aligned}
\end{equation}
Expanding the dual electromagnetic field, first in terms of the spatial vectors, and then in the space time basis, we have
\begin{equation}\label{eqn:maxwellStokes:520}
\begin{aligned}
G
&= -I F \\
&= -I \lr{ \BE + I c \BB } \\
&= -I \BE + c \BB. \\
&= -I \BE + c B^k \gamma_k \gamma_0 \\
&= \inv{2} \epsilon^{r s t} \gamma_r \gamma_s E^t + c B^k \gamma_k \gamma_0.
\end{aligned}
\end{equation}
So, dotting with a spatial vector will pick up a component of \( \BB \), we have
\begin{equation}\label{eqn:maxwellStokes:540}
\begin{aligned}
\lr{ \gamma_m \wedge \gamma_0 } \cdot \partial_\mu G
&=
\lr{ \gamma_m \wedge \gamma_0 } \cdot \partial_\mu \lr{
\inv{2} \epsilon^{r s t} \gamma_r \gamma_s E^t + c B^k \gamma_k \gamma_0
} \\
&=
c \partial_\mu B^k
\gpgradezero{
\gamma_m \gamma_0 \gamma_k \gamma_0
} \\
&=
c \partial_\mu B^k
\gpgradezero{
\gamma_m \gamma_0 \gamma_0 \gamma^k
} \\
&=
c \partial_\mu B^k
\delta_m^k \\
&=
c \partial_\mu B^m.
\end{aligned}
\end{equation}
Written out explicitly the electric field contributions to \( G \) are
\begin{equation}\label{eqn:maxwellStokes:560}
\begin{aligned}
-I \BE
&=
-\gamma_{0123k0} E^k \\
&=
-\gamma_{123k} E^k \\
&=
\left\{
\begin{array}{l l}
\gamma_{12} E^3 & \quad \mbox{\( k = 3 \)} \\
\gamma_{31} E^2 & \quad \mbox{\( k = 2 \)} \\
\gamma_{23} E^1 & \quad \mbox{\( k = 1 \)} \\
\end{array}
\right.,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:maxwellStokes:580}
\begin{aligned}
\gamma_{23} \cdot G &= -E^1 \\
\gamma_{31} \cdot G &= -E^2 \\
\gamma_{12} \cdot G &= -E^3.
\end{aligned}
\end{equation}
We now have the pieces required to expand \ref{eqn:maxwellStokes:500} and \ref{eqn:maxwellStokes:620}, which are respectively
\begin{equation}\label{eqn:maxwellStokes:501}
\begin{aligned}
– c \partial_2 B^1 + c \partial_1 B^2 – \partial_0 E^3 &= \inv{\epsilon_0 c} J^3 \\
– c \partial_3 B^1 + c \partial_1 B^3 + \partial_0 E^2 &= -\inv{\epsilon_0 c} J^2 \\
– c \partial_3 B^2 + c \partial_2 B^3 – \partial_0 E^1 &= \inv{\epsilon_0 c} J^1 \\
– \partial_3 E^3 – \partial_2 E^2 – \partial_1 E^1 &= – \inv{\epsilon_0} \rho
\end{aligned}
\end{equation}
which are the components of the Ampere-Maxwell equation, and Gauss’s law
\begin{equation}\label{eqn:maxwellStokes:600}
\begin{aligned}
\inv{\mu_0} \spacegrad \cross \BB – \epsilon_0 \PD{t}{\BE} &= \BJ \\
\spacegrad \cdot \BE &= \frac{\rho}{\epsilon_0}.
\end{aligned}
\end{equation}
Problem 2:
Prove \ref{eqn:maxwellStokes:180}.
Answer
The proof just requires the expansion of the dot products using scalar selection
\begin{equation}\label{eqn:maxwellStokes:260}
\begin{aligned}
d^2 x \cdot G
&=
\gpgradezero{ d^2 x (-I) F } \\
&=
-\gpgradezero{ I d^2 x F } \\
&=
-I \lr{ d^2 x \wedge F },
\end{aligned}
\end{equation}
and
for the three volume dot product
\begin{equation}\label{eqn:maxwellStokes:280}
\begin{aligned}
d^3 x \cdot (I J)
&=
\gpgradezero{
d^3 x\, I J
} \\
&=
-\gpgradezero{
I d^3 x\, J
} \\
&=
-I \lr{ d^3 x \wedge J }.
\end{aligned}
\end{equation}
Problem 3:
Using each of the four possible spacetime volume elements, write out the components of the Stokes integral
\ref{eqn:maxwellStokes:180}.
Answer
The four possible volume and associated area elements are
\begin{equation}\label{eqn:maxwellStokes:220}
\begin{aligned}
d^3 x = c \gamma_0 \gamma_1 \gamma_2 dt dx dy & \qquad d^2 x = \gamma_1 \gamma_2 dx dy + c \gamma_2 \gamma_0 dy dt + c \gamma_0 \gamma_1 dt dx \\
d^3 x = c \gamma_0 \gamma_1 \gamma_3 dt dx dz & \qquad d^2 x = \gamma_1 \gamma_3 dx dz + c \gamma_3 \gamma_0 dz dt + c \gamma_0 \gamma_1 dt dx \\
d^3 x = c \gamma_0 \gamma_2 \gamma_3 dt dy dz & \qquad d^2 x = \gamma_2 \gamma_3 dy dz + c \gamma_3 \gamma_0 dz dt + c \gamma_0 \gamma_2 dt dy \\
d^3 x = \gamma_1 \gamma_2 \gamma_3 dx dy dz & \qquad d^2 x = \gamma_1 \gamma_2 dx dy + \gamma_2 \gamma_3 dy dz + c \gamma_3 \gamma_1 dz dx \\
\end{aligned}
\end{equation}
Wedging the area element with \( F \) will produce pseudoscalar multiples of the various \( \BE \) and \( \BB \) components, but a recipe for these components is required.
First note that for \( k \ne 0 \), the wedge \( \gamma_k \wedge \gamma_0 \wedge F \) will just select components of \( \BB \). This can be seen first by simplifying
\begin{equation}\label{eqn:maxwellStokes:300}
\begin{aligned}
I \BB
&=
\gamma_{0 1 2 3} B^m \gamma_{m 0} \\
&=
\left\{
\begin{array}{l l}
\gamma_{3 2} B^1 & \quad \mbox{\( m = 1 \)} \\
\gamma_{1 3} B^2 & \quad \mbox{\( m = 2 \)} \\
\gamma_{2 1} B^3 & \quad \mbox{\( m = 3 \)}
\end{array}
\right.,
\end{aligned}
\end{equation}
or
\begin{equation}\label{eqn:maxwellStokes:320}
I \BB = – \epsilon_{a b c} \gamma_{a b} B^c.
\end{equation}
From this it follows that
\begin{equation}\label{eqn:maxwellStokes:340}
\gamma_k \wedge \gamma_0 \wedge F = I c B^k.
\end{equation}
The electric field components are easier to pick out. Those are selected by
\begin{equation}\label{eqn:maxwellStokes:360}
\begin{aligned}
\gamma_m \wedge \gamma_n \wedge F
&= \gamma_m \wedge \gamma_n \wedge \gamma_k \wedge \gamma_0 E^k \\
&= -I E^k \epsilon_{m n k}.
\end{aligned}
\end{equation}
The respective volume element wedge products with \( J \) are
\begin{equation}\label{eqn:maxwellStokes:400}
\begin{aligned}
\inv{I} d^3 x \wedge J = \inv{c \epsilon_0} J^3
\inv{I} d^3 x \wedge J = \inv{c \epsilon_0} J^2
\inv{I} d^3 x \wedge J = \inv{c \epsilon_0} J^1,
\end{aligned}
\end{equation}
and the respective sum of surface area elements wedged with the electromagnetic field are
\begin{equation}\label{eqn:maxwellStokes:380}
\begin{aligned}
\inv{I} d^2 x \wedge F &= – \evalbar{E^3}{c \Delta t} dx dy + c \lr{ \evalbar{B^2}{\Delta x} dy – \evalbar{B^1}{\Delta y} dx } dt \\
\inv{I} d^2 x \wedge F &= \evalbar{E^2}{c \Delta t} dx dz + c \lr{ \evalbar{B^3}{\Delta x} dz – \evalbar{B^1}{\Delta z} dx } dt \\
\inv{I} d^2 x \wedge F &= – \evalbar{E^1}{c \Delta t} dy dz + c \lr{ \evalbar{B^3}{\Delta y} dz – \evalbar{B^2}{\Delta z} dy } dt \\
\inv{I} d^2 x \wedge F &= – \evalbar{E^3}{\Delta z} dy dx – \evalbar{E^2}{\Delta y} dx dz – \evalbar{E^1}{\Delta x} dz dy,
\end{aligned}
\end{equation}
so
\begin{equation}\label{eqn:maxwellStokes:381}
\begin{aligned}
\int_{\partial V} – \evalbar{E^3}{c \Delta t} dx dy + c \lr{ \evalbar{B^2}{\Delta x} dy – \evalbar{B^1}{\Delta y} dx } dt &=
c \int_V dx dy dt \inv{c \epsilon_0} J^3 \\
\int_{\partial V} \evalbar{E^2}{c \Delta t} dx dz + c \lr{ \evalbar{B^3}{\Delta x} dz – \evalbar{B^1}{\Delta z} dx } dt &=
-c \int_V dx dy dt \inv{c \epsilon_0} J^2 \\
\int_{\partial V} – \evalbar{E^1}{c \Delta t} dy dz + c \lr{ \evalbar{B^3}{\Delta y} dz – \evalbar{B^2}{\Delta z} dy } dt &=
c \int_V dx dy dt \inv{c \epsilon_0} J^1 \\
\int_{\partial V} – \evalbar{E^3}{\Delta z} dy dx – \evalbar{E^2}{\Delta y} dx dz – \evalbar{E^1}{\Delta x} dz dy &=
-\int_V dx dy dz \inv{\epsilon_0} \rho.
\end{aligned}
\end{equation}
Observe that if the volume elements are taken to their infinesimal limits, we recover the traditional differential forms of the Ampere-Maxwell and Gauss’s law equations.
References
[1] A. Macdonald. Vector and Geometric Calculus. CreateSpace Independent Publishing Platform, 2012.
Like this:
Like Loading...