Quantum Mechanics

Geometric algebra notes collection split into two volumes

November 10, 2015 math and physics play , , , , , , , , , , , , ,

I’ve now split my (way too big) Exploring physics with Geometric Algebra into two volumes:

Each of these is now a much more manageable size, which should facilitate removing the redundancies in these notes, and making them more properly book like.

Also note I’ve also previously moved “Exploring Geometric Algebra” content related to:

  • Lagrangian’s
  • Hamiltonian’s
  • Noether’s theorem

into my classical mechanics collection (449 pages).

PHY1520H Graduate Quantum Mechanics. Lecture 11: Symmetries in QM. Taught by Prof. Arun Paramekanti

October 29, 2015 phy1520 , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course PHY1520, Graduate Quantum Mechanics, taught by Prof. Paramekanti, covering \textchapref{{4}} [1] content.

Symmetry in classical mechanics

In a classical context considering a Hamiltonian

\begin{equation}\label{eqn:qmLecture11:20}
H(q_i, p_i),
\end{equation}

a symmetry means that certain \( q_i \) don’t appear. In that case the rate of change of one of the generalized momenta is zero

\begin{equation}\label{eqn:qmLecture11:40}
\ddt{p_k} = – \PD{q_k}{H} = 0,
\end{equation}

so \( p_k \) is a constant of motion. This simplifies the problem by reducing the number of degrees of freedom. Another aspect of such a symmetry is that it \underline{relates trajectories}. For example, assuming a rotational symmetry as in fig. 1.

fig. 1. Trajectory under rotational symmetry

fig. 1. Trajectory under rotational symmetry

the trajectory of a particle after rotation is related by rotation to the trajectory of the unrotated particle.

Symmetry in quantum mechanics

Suppose that we have a symmetry operation that takes states from

\begin{equation}\label{eqn:qmLecture11:60}
\ket{\psi} \rightarrow \ket{U \psi}
\end{equation}
\begin{equation}\label{eqn:qmLecture11:80}
\ket{\phi} \rightarrow \ket{U \phi},
\end{equation}

we expect that

\begin{equation}\label{eqn:qmLecture11:100}
\Abs{\braket{ \psi}{\phi} }^2 = \Abs{\braket{ U\psi}{ U\phi} }^2.
\end{equation}

This won’t hold true for a general operator. Two cases where this does hold true is when

  • \( \braket{\psi}{\phi} = \braket{ U\psi}{ U\phi} \). Here \( U \) is unitary, and the equivalence follows from

    \begin{equation}\label{eqn:qmLecture11:120}
    \braket{ U\psi}{ U\phi} = \bra{ \psi} U^\dagger U { \phi} = \bra{ \psi} 1 { \phi} = \braket{\psi}{\phi}.
    \end{equation}

  • \( \braket{\psi}{\phi} = \braket{ U\psi}{ U\phi}^\conj \). Here \( U \) is anti-unitary.

Unitary case

If an “observable” is not changed by a unitary operation representing a symmetry we must have

\begin{equation}\label{eqn:qmLecture11:140}
\bra{\psi} \hat{A} \ket{\psi}
\rightarrow
\bra{U \psi} \hat{A} \ket{U \psi}
=
\bra{\psi} U^\dagger \hat{A} U \ket{\psi},
\end{equation}

so
\begin{equation}\label{eqn:qmLecture11:160}
U^\dagger \hat{A} U = \hat{A},
\end{equation}

or
\begin{equation}\label{eqn:qmLecture11:180}
\boxed{
\hat{A} U = U \hat{A}.
}
\end{equation}

An observable that is unchanged by a unitary symmetry commutes \( \antisymmetric{\hat{A}}{U} \) with the operator \( U \) for that transformation.

Symmetries of the Hamiltonian

Given
\begin{equation}\label{eqn:qmLecture11:200}
\antisymmetric{H}{U} = 0,
\end{equation}

\( H \) is invariant.

Given

\begin{equation}\label{eqn:qmLecture11:220}
H \ket{\phi_n} = \epsilon_n \ket{\phi_n} .
\end{equation}

\begin{equation}\label{eqn:qmLecture11:240}
\begin{aligned}
U H \ket{\phi_n}
&= H U \ket{\phi_n} \\
&= \epsilon_n U \ket{\phi_n}
\end{aligned}
\end{equation}

Such a state

\begin{equation}\label{eqn:qmLecture11:260}
\ket{\psi_n} = U \ket{\phi_n}
\end{equation}

is also an eigenstate with the \underline{same} energy.

Suppose this process is repeated, finding other states

\begin{equation}\label{eqn:qmLecture11:280}
U \ket{\psi_n} = \ket{\chi_n}
\end{equation}
\begin{equation}\label{eqn:qmLecture11:300}
U \ket{\chi_n} = \ket{\alpha_n}
\end{equation}

Because such a transformation only generates states with the initial energy, this process cannot continue forever. At some point this process will enumerate a fixed size set of states. These states can be orthonormalized.

We can say that symmetry operations are generators of a \underlineAndIndex{group}. For a set of symmetry operations we can

  • Form products that lie in a closed set

    \begin{equation}\label{eqn:qmLecture11:320}
    U_1 U_2 = U_3
    \end{equation}

  • can define an inverse
    \begin{equation}\label{eqn:qmLecture11:340}
    U \leftrightarrow U^{-1}.
    \end{equation}

  • obeys associative rules for multiplication
    \begin{equation}\label{eqn:qmLecture11:360}
    U_1 ( U_2 U_3 ) = (U_1 U_2) U_3.
    \end{equation}

  • has an identity operation.

When \( H \) has a symmetry, then degenerate eigenstates form \underlineAndIndex{irreducible} representations (which cannot be further block diagonalized).

Some simple examples

Example: Inversion.

{example:qmLecture11:1}

Given a state and a parity operation \( \hat{\Pi} \), with the transformation

\begin{equation}\label{eqn:qmLecture11:380}
\ket{\psi} \rightarrow \hat{\Pi} \ket{\psi}
\end{equation}

In one dimension, the parity operation is just inversion. In two dimensions, this is a set of flipping operations on two axes fig. 2.

fig. 2. 2D parity operation

fig. 2. 2D parity operation

The operational effects of this operator are

\begin{equation}\label{eqn:qmLecture11:400}
\begin{aligned}
\hat{x} &\rightarrow – \hat{x} \\
\hat{p} &\rightarrow – \hat{p}.
\end{aligned}
\end{equation}

Acting again with the parity operator produces the original value, so it is its own inverse, and \( \hat{\Pi}^\dagger = \hat{\Pi} = \hat{\Pi}^{-1} \). In an expectation value

\begin{equation}\label{eqn:qmLecture11:420}
\bra{ \hat{\Pi} \psi } \hat{x} \ket{ \hat{\Pi} \psi } = – \bra{\psi} \hat{x} \ket{\psi}.
\end{equation}

This means that

\begin{equation}\label{eqn:qmLecture11:440}
\hat{\Pi}^\dagger \hat{x} \hat{\Pi} = – \hat{x},
\end{equation}

or
\begin{equation}\label{eqn:qmLecture11:460}
\hat{x} \hat{\Pi} = – \hat{\Pi} \hat{x},
\end{equation}

\begin{equation}\label{eqn:qmLecture11:480}
\begin{aligned}
\hat{x} \hat{\Pi} \ket{x_0}
&= – \hat{\Pi} \hat{x} \ket{x_0} \\
&= – \hat{\Pi} x_0 \ket{x_0} \\
&= – x_0 \hat{\Pi} \ket{x_0}
\end{aligned}
\end{equation}

so

\begin{equation}\label{eqn:qmLecture11:500}
\hat{\Pi} \ket{x_0} = \ket{-x_0}.
\end{equation}

Acting on a wave function

\begin{equation}\label{eqn:qmLecture11:520}
\begin{aligned}
\bra{x} \hat{\Pi} \ket{\psi}
&=
\braket{-x}{\psi} \\
&= \psi(-x).
\end{aligned}
\end{equation}

What does this mean for eigenfunctions. Eigenfunctions are supposed to form irreducible representations of the group. The group has just two elements

\begin{equation}\label{eqn:qmLecture11:540}
\setlr{ 1, \hat{\Pi} },
\end{equation}

where \( \hat{\Pi}^2 = 1 \).

Suppose we have a Hamiltonian

\begin{equation}\label{eqn:qmLecture11:560}
H = \frac{\hat{p}^2}{2m} + V(\hat{x}),
\end{equation}

where \( V(\hat{x}) \) is even ( \( \antisymmetric{V(\hat{x})}{\hat{\Pi} } = 0 \) ). The squared momentum commutes with the parity operator

\begin{equation}\label{eqn:qmLecture11:580}
\begin{aligned}
\antisymmetric{\hat{p}^2}{\hat{\Pi}}
&=
\hat{p}^2 \hat{\Pi}
– \hat{\Pi} \hat{p}^2 \\
&=
\hat{p}^2 \hat{\Pi}
– (\hat{\Pi} \hat{p}) \hat{p} \\
&=
\hat{p}^2 \hat{\Pi}
-(- \hat{p} \hat{\Pi}) \hat{p} \\
&=
\hat{p}^2 \hat{\Pi}
+ \hat{p} (-\hat{p} \hat{\Pi}) \\
&=
0.
\end{aligned}
\end{equation}

Only two functions are possible in the symmetry set \( \setlr{ \Psi(x), \hat{\Pi} \Psi(x) } \), since

\begin{equation}\label{eqn:qmLecture11:600}
\begin{aligned}
\hat{\Pi}^2 \Psi(x)
&= \hat{\Pi} \Psi(-x) \\
&= \Psi(x).
\end{aligned}
\end{equation}

This symmetry severely restricts the possible solutions, making it so there can be only one dimensional forms of this problem with solutions that are either even or odd respectively

\begin{equation}\label{eqn:qmLecture11:620}
\begin{aligned}
\phi_e(x) &= \psi(x ) + \psi(-x) \\
\phi_o(x) &= \psi(x ) – \psi(-x).
\end{aligned}
\end{equation}

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

First update of aggregate notes for phy1520, Graduate Quantum Mechanics

October 2, 2015 phy1520 ,

I’ve posted a first update of my aggregate notes for PHY1520H Graduate Quantum Mechanics, taught by Prof. Arun Paramekanti. This includes lecture notes up to lecture 5, my ungraded solutions for the first problem set, and a number of worked problems from chapter 1 and 2 of Sakurai done as review preparation for the course (since I hadn’t done QM since 2011).

Most of the content was posted individually in the following locations. Bug fixes and enhancements to the original documents will only be made in the aggregate notes.

PHY1520H Graduate Quantum Mechanics. Lecture 1: Lighting review. Taught by Prof. Arun Paramekanti

September 17, 2015 phy1520 , , , , , , , , , , , , , ,

[Click here for a PDF of this post with nicer formatting]

Disclaimer

Peeter’s lecture notes from class. These may be incoherent and rough.

These are notes for the UofT course PHY1520, Graduate Quantum Mechanics, taught by Prof. Paramekanti, covering [1] chap. 1 content.

Classical mechanics

We’ll be talking about one body physics for most of this course. In classical mechanics we can figure out the particle trajectories using both of \( (\Br, \Bp \), where

\begin{equation}\label{eqn:qmLecture1:20}
\begin{aligned}
\ddt{\Br} &= \inv{m} \Bp \\
\ddt{\Bp} &= \spacegrad V
\end{aligned}
\end{equation}

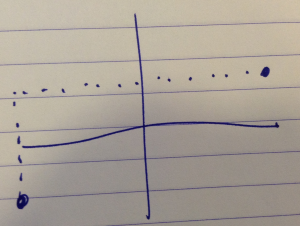
A two dimensional phase space as sketched in fig. 1 shows the trajectory of a point particle subject to some equations of motion

lectureOnePhaseSpaceClassicalFig1

fig. 1. One dimensional classical phase space example

Quantum mechanics

For this lecture, we’ll work with natural units, setting

\begin{equation}\label{eqn:qmLecture1:480}
\boxed{
\Hbar = 1.
}
\end{equation}

In QM we are no longer allowed to think of position and momentum, but have to start asking about state vectors \( \ket{\Psi} \).

We’ll consider the state vector with respect to some basis, for example, in a position basis, we write

\begin{equation}\label{eqn:qmLecture1:40}
\braket{ x }{\Psi } = \Psi(x),
\end{equation}

a complex numbered “wave function”, the probability amplitude for a particle in \( \ket{\Psi} \) to be in the vicinity of \( x \).

We could also consider the state in a momentum basis

\begin{equation}\label{eqn:qmLecture1:60}
\braket{ p }{\Psi } = \Psi(p),
\end{equation}

a probability amplitude with respect to momentum \( p \).

More precisely,

\begin{equation}\label{eqn:qmLecture1:80}
\Abs{\Psi(x)}^2 dx \ge 0
\end{equation}

is the probability of finding the particle in the range \( (x, x + dx ) \). To have meaning as a probability, we require

\begin{equation}\label{eqn:qmLecture1:100}
\int_{-\infty}^\infty \Abs{\Psi(x)}^2 dx = 1.
\end{equation}

The average position can be calculated using this probability density function. For example

\begin{equation}\label{eqn:qmLecture1:120}
\expectation{x} = \int_{-\infty}^\infty \Abs{\Psi(x)}^2 x dx,
\end{equation}

or
\begin{equation}\label{eqn:qmLecture1:140}
\expectation{f(x)} = \int_{-\infty}^\infty \Abs{\Psi(x)}^2 f(x) dx.
\end{equation}

Similarly, calculation of an average of a function of momentum can be expressed as

\begin{equation}\label{eqn:qmLecture1:160}
\expectation{f(p)} = \int_{-\infty}^\infty \Abs{\Psi(p)}^2 f(p) dp.
\end{equation}

Transformation from a position to momentum basis

We have a problem, if we which to compute an average in momentum space such as \( \expectation{p} \), when given a wavefunction \( \Psi(x) \).

How do we convert

\begin{equation}\label{eqn:qmLecture1:180}
\Psi(p)
\stackrel{?}{\leftrightarrow}
\Psi(x),
\end{equation}

or equivalently
\begin{equation}\label{eqn:qmLecture1:200}
\braket{p}{\Psi}
\stackrel{?}{\leftrightarrow}
\braket{x}{\Psi}.
\end{equation}

Such a conversion can be performed by virtue of an the assumption that we have a complete orthonormal basis, for which we can introduce identity operations such as

\begin{equation}\label{eqn:qmLecture1:220}
\int_{-\infty}^\infty dp \ket{p}\bra{p} = 1,
\end{equation}

or
\begin{equation}\label{eqn:qmLecture1:240}
\int_{-\infty}^\infty dx \ket{x}\bra{x} = 1
\end{equation}

Some interpretations:

  1. \( \ket{x_0} \leftrightarrow \text{sits at} x = x_0 \)
  2. \( \braket{x}{x’} \leftrightarrow \delta(x – x’) \)
  3. \( \braket{p}{p’} \leftrightarrow \delta(p – p’) \)
  4. \( \braket{x}{p’} = \frac{e^{i p x}}{\sqrt{V}} \), where \( V \) is the volume of the box containing the particle. We’ll define the appropriate normalization for an infinite box volume later.

The delta function interpretation of the braket \( \braket{p}{p’} \) justifies the identity operator, since we recover any state in the basis when operating with it. For example, in momentum space

\begin{equation}\label{eqn:qmLecture1:260}
\begin{aligned}
1 \ket{p}
&=
\lr{ \int_{-\infty}^\infty dp’
\ket{p’}\bra{p’} }
\ket{p} \\
&=
\int_{-\infty}^\infty dp’
\ket{p’}
\braket{p’}{p} \\
&=
\int_{-\infty}^\infty dp’
\ket{p’}
\delta(p – p’) \\
&=
\ket{p}.
\end{aligned}
\end{equation}

This also the determination of an integral operator representation for the delta function

\begin{equation}\label{eqn:qmLecture1:500}
\begin{aligned}
\delta(x – x’)
&=
\braket{x}{x’} \\
&=
\int dp \braket{x}{p} \braket{p}{x’} \\
&=
\inv{V} \int dp e^{i p x} e^{-i p x’},
\end{aligned}
\end{equation}

or

\begin{equation}\label{eqn:qmLecture1:520}
\delta(x – x’)
=
\inv{V} \int dp e^{i p (x- x’)}.
\end{equation}

Here we used the fact that \( \braket{p}{x} = \braket{x}{p}^\conj \).

FIXME: do we have a justification for that conjugation with what was defined here so far?

The conversion from a position basis to momentum space is now possible

\begin{equation}\label{eqn:qmLecture1:280}
\begin{aligned}
\braket{p}{\Psi}
&= \Psi(p) \\
&= \int_{-\infty}^\infty \braket{p}{x} \braket{x}{\Psi} dx \\
&= \int_{-\infty}^\infty \frac{e^{-ip x}}{\sqrt{V}} \Psi(x) dx.
\end{aligned}
\end{equation}

The momentum space to position space conversion can be written as

\begin{equation}\label{eqn:qmLecture1:300}
\Psi(x)
= \int_{-\infty}^\infty \frac{e^{ip x}}{\sqrt{V}} \Psi(p) dp.
\end{equation}

Now we can go back and figure out the an expectation

\begin{equation}\label{eqn:qmLecture1:320}
\begin{aligned}
\expectation{p}
&=
\int \Psi^\conj(p) \Psi(p) p d p \\
&=
\int dp
\lr{
\int_{-\infty}^\infty \frac{e^{ip x}}{\sqrt{V}} \Psi^\conj(x) dx
}
\lr{
\int_{-\infty}^\infty \frac{e^{-ip x’}}{\sqrt{V}} \Psi(x’) dx’
}
p \\
&=\int dp dx dx’
\Psi^\conj(x)
\inv{V} e^{ip (x-x’)} \Psi(x’) p \\
&=
\int dp dx dx’
\Psi^\conj(x)
\inv{V} \lr{ -i\PD{x}{e^{ip (x-x’)}} }\Psi(x’) \\
&=
\int dp dx
\Psi^\conj(x) \lr{ -i \PD{x}{} }
\inv{V} \int dx’ e^{ip (x-x’)} \Psi(x’) \\
&=
\int dx
\Psi^\conj(x) \lr{ -i \PD{x}{} }
\int dx’ \lr{ \inv{V} \int dp e^{ip (x-x’)} } \Psi(x’) \\
&=
\int dx
\Psi^\conj(x) \lr{ -i \PD{x}{} }
\int dx’ \delta(x – x’) \Psi(x’) \\
&=
\int dx
\Psi^\conj(x) \lr{ -i \PD{x}{} }
\Psi(x)
\end{aligned}
\end{equation}

Here we’ve essentially calculated the position space representation of the momentum operator, allowing identifications of the following form

\begin{equation}\label{eqn:qmLecture1:380}
p \leftrightarrow -i \PD{x}{}
\end{equation}
\begin{equation}\label{eqn:qmLecture1:400}
p^2 \leftrightarrow – \PDSq{x}{}.
\end{equation}

Alternate starting point.

Most of the above results followed from the claim that \( \braket{x}{p} = e^{i p x} \). Note that this position space representation of the momentum operator can also be taken as the starting point. Given that, the exponential representation of the position-momentum braket follows

\begin{equation}\label{eqn:qmLecture1:540}
\bra{x} P \ket{p}
=
-i \Hbar \PD{x}{} \braket{x}{p},
\end{equation}

but \( \bra{x} P \ket{p} = p \braket{x}{p} \), providing a differential equation for \( \braket{x}{p} \)

\begin{equation}\label{eqn:qmLecture1:560}
p \braket{x}{p} = -i \Hbar \PD{x}{} \braket{x}{p},
\end{equation}

with solution

\begin{equation}\label{eqn:qmLecture1:580}
i p x/\Hbar = \ln \braket{x}{p} + \text{const},
\end{equation}

or
\begin{equation}\label{eqn:qmLecture1:600}
\braket{x}{p} \propto e^{i p x/\Hbar}.
\end{equation}

Matrix interpretation

  1. Ket’s \( \ket{\Psi} \leftrightarrow \text{column vector} \)
  2. Bra’s \( \bra{\Psi} \leftrightarrow {(\text{row vector})}^\conj \)
  3. Operators \( \leftrightarrow \) matrices that act on vectors.

\begin{equation}\label{eqn:qmLecture1:420}
\hat{p} \ket{\Psi} \rightarrow \ket{\Psi’}
\end{equation}

Time evolution

For a state subject to the equations of motion given by the Hamiltonian operator \( \hat{H} \)

\begin{equation}\label{eqn:qmLecture1:440}
i \PD{t}{} \ket{\Psi} = \hat{H} \ket{\Psi},
\end{equation}

the time evolution is given by
\begin{equation}\label{eqn:qmLecture1:460}
\ket{\Psi(t)} = e^{-i \hat{H} t} \ket{\Psi(0)}.
\end{equation}

Incomplete information

We’ll need to introduce the concept of Density matrices. This will bring us to concepts like entanglement.

References

[1] Jun John Sakurai and Jim J Napolitano. Modern quantum mechanics. Pearson Higher Ed, 2014.

Update to old phy356 (Quantum Mechanics I) notes.

February 12, 2015 math and physics play , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,

It’s been a long time since I took QM I. My notes from that class were pretty rough, but I’ve cleaned them up a bit.

The main value to these notes is that I worked a number of introductory Quantum Mechanics problems.

These were my personal lecture notes for the Fall 2010, University of Toronto Quantum mechanics I course (PHY356H1F), taught by Prof. Vatche Deyirmenjian.

The official description of this course was:

The general structure of wave mechanics; eigenfunctions and eigenvalues; operators; orbital angular momentum; spherical harmonics; central potential; separation of variables, hydrogen atom; Dirac notation; operator methods; harmonic oscillator and spin.

This document contains a few things

• My lecture notes.
Typos, if any, are probably mine(Peeter), and no claim nor attempt of spelling or grammar correctness will be made. The first four lectures had chosen not to take notes for since they followed the text very closely.
• Notes from reading of the text. This includes observations, notes on what seem like errors, and some solved problems. None of these problems have been graded. Note that my informal errata sheet for the text has been separated out from this document.
• Some assigned problems. I have corrected some the errors after receiving grading feedback, and where I have not done so I at least recorded some of the grading comments as a reference.
• Some worked problems associated with exam preparation.